基于再分析数据的南大洋区域Ekman流时空分布规律研究*

林辉义 高艳秋 张继才

基于再分析数据的南大洋区域Ekman流时空分布规律研究*

林辉义1高艳秋2张继才1①

(1. 浙江大学海洋学院物理海洋与遥感研究所 舟山 316021; 2. 自然资源部第二海洋研究所卫星海洋环境动力学国家重点实验室 杭州 310012)

南大洋Ekman输运是全球大气-海洋耦合气候系统的重要组成部分, 对该区域Ekman动力过程的研究极为重要。首先基于实测数据和文献资料, 对GEKCO2 (Geostrophic and Ekman Current Observatory 2) 产品提供的Ekman流数据进行了评估, 验证了数据的有效性; 并结合CCMP(cross-calibrated multi-platform)、ERA5(the fifth generation European centre for medium-range weather forecasts atmospheric reanalysis)风场数据, 采用经验正交函数分析法(empirical orthogonal function, EOF)等方法分析了2010—2018年南大洋Ekman流的时空变化规律。结果表明: (1)南大洋Ekman流速集中在9—11 cm/s, 且具有很强的月际变化特征(7月最强, 12月最弱); (2)南大洋40°S以北海域是Ekman流速随时间变化较大的区域; (3)南大洋Ekman流速的EOF分析显示: 第一模态和风场存在较强的相关性, 表现为流速在整体上同时增强或减弱; 第二模态和南半球中高纬大气环流存在较强的相关性, 表现为以50°S为界南北流速反向变化; (4)Ekman流左偏角度集中在60°—75°, 其中概率密度最大值处所对应的角度为67.5°。通过矢量相关分析, 得到30°—35°S海域的平均偏角存在月际变化。南大洋的Ekman动力过程对海洋环流和全球气候系统具有重大影响, 本文对于进一步理解南大洋的Ekman过程具有一定的参考价值。

南大洋; Ekman流; 时空变化; 经验正交函数分析法; 海表洋流产品GEKCO2

Ekman理论(Ekman, 1905)是物理海洋学的奠基性理论之一(McWilliams, 2006)。根据严格的数学求解, Ekman流在北(南)半球随深度增加呈螺旋状顺(逆)时针旋转, 表层流速偏向风的右(左)侧约45°。为提高Ekman理论与实测数据的符合度, 许多研究对经典Ekman理论做了很好的补充与修正, 比如加入水平浮力梯度项(Cronin, 2009; Wenegrat, 2016), 考虑波浪效应(Zhang, 2019b; Hui, 2016)、加入非线性效应(Constantin, 2019), 将涡黏系数设为随时间或随深度变化的量(Zhang, 2019a; Constantin, 2021)。

前人的研究表明, Ekman动力过程对海洋环流和全球气候系统具有重大影响。Speer等(2000)指出Ekman输运通过驱动50°S附近的深水上涌并向北运输, 在经向翻转环流中发挥着重要作用。这些Ekman流将冷水向北输送, 影响了极地的热量输送, 从而促进了全球的热量平衡。Lenn等(2009)指出南大洋区域Ekman层构成了南极绕极流及该区域经向翻转流的最浅部分, 而南极绕极流是地球上唯一一支和所有其他洋流都有关系的洋流, 是全球气候系统的重要组成部分。综上所述, 研究南大洋区域的Ekman动力过程和Ekman流的时空分布特征具有重要的科学价值。

由于南大洋区域的大气和海洋动力机制异常复杂, 观测难度很大, 基于观测数据对该区域Ekman动力过程进行研究的工作较少。Lenn等(2009)使用德雷克海峡的声学多普勒流速剖面仪(acoustic doppler current profiler, ADCP)实测数据提取Ekman流, 并计算了随深度变化的涡黏系数; Polton等(2013)用地转剪切的方法从该ADCP数据中重新提取Ekman流, 提取结果与经典的Ekman理论(恒定的涡黏系数)相一致; Elipot等(2009)用频谱方法将多个不同的Ekman模型与漂流浮标数据进行匹配, 结果表明将涡黏系数设为恒定, 且Ekman流速在Ekman层深度处衰减为零时的匹配效果最佳; Roach等(2015)使用恒定涡黏系数的Ekman模型描述克格伦以北的南极绕极流进入上层海洋的动力过程。

前文所述的工作基本基于少数的航线定点观测剖面或者浮标观测, 虽然能得到Ekman流的垂直结构, 但是不适用于描述南大洋大范围、长时间的Ekman动力过程。近些年, 遥感技术和相关理论的发展为人们研究Ekman流的时空分布特征提供了可能, Lagerloef等(1999)、Bonjean等(2002)、Sudre等(2013)、Hui等(2016)从卫星遥感数据反演得到表层流场(地转流和Ekman流之和), 其中Ekman流由海表风场数据得到。刘巍等(2012)和安玉柱等(2012)基于卫星遥感资料估算全球海表Ekman流时引入了权重函数, 解决了Lagerloef方法中Ekman流在25°S和25°N上的不连续问题。在海表流场数据产品方面, 由法国 LEGOS (laboratoire d’Etudes en géophysique et océanographie spatiales)发布的GEKCO2 (Geostrophic and Ekman Current Observatory 2)数据(详细介绍见1.2节)提供了高分辨率海表流场数据。

综上所述, 尽管南大洋Ekman过程对海洋动力系统和全球气候都有着重要的影响, 但是极大的观测难度使得人们无法通过实测资料研究其大尺度的时间和空间变化。基于上述问题, 本文在采用南大洋浮标数据评估GEKCO2数据有效性的基础上, 开展南大洋区域Ekman流速、偏向角的时空变化特征研究, 重点分析Ekman流速月际变化特征, 以及不同区域流速的差异性; 并结合CCMP(cross-calibrated multi-platform)、ERA5(the fifth generation European centre for medium-range weather forecasts atmospheric reanalysis)再分析风场资料, 讨论Ekman流偏向角度的时空变化特征。本文结构如下: 第1部分介绍了本文所用数据资料以及所选研究区域; 第2部分采用实测资料评估GEKCO2数据有效性, 并分析了Ekman流速、偏向角度的时空变化特征; 第3部分是对本文的总结。

1 研究区域与数据

1.1 研究区域

南大洋是指太平洋、大西洋、印度洋的南部互相连通的海域(图1a), 是世界上唯一完全环绕地球却未被大陆分割的大洋, 独特的地形结构造就了全球唯一的绕极环流 (Antarctic circumpolar current, ACC)。ACC将海水从西向东输送, 流量超过100 Sv(Nowlin, 1986), 形成了各大洋间最强的水交换, 如一条纽带连结起全球的热盐环流(史久新, 2000)。

图1 南大洋地形图(a)和数据有效区域(b)

注: 图1b蓝色区域为数据有效区域, 粉色区域为舍弃区域

1.2 GEKCO2数据

本文采用了法国LEGOS(http://www.legos.obs- mip.fr/)提供的GEKCO2数据探讨南大洋Ekman流的时空变化特征。该数据集提供了海表流速(c)、Ekman流(e)以及地转流(g), 其中Ekman流由CERSAT(centre ERS d′Archivage et de traitement)发布的QuickScat(quick scatterometer)/ASCAT(advanced scatterometer)风场数据计算得到, 地转流由法国AVISO(archiving, validation and interpretation of satellite oceanographic data)发布的绝对动态地形MADT(maps of absolute dynamic topography)计算得到。本文选取的GEKCO2数据空间范围为29.875°—70.125°S, 0°—359.75E°(图1b), 分辨率为0.25°×0.25°; 时间范围为2009年11月到2019年2月共3 407 d, 分辨率为1 d。

GEKCO2数据假设海表流速是Ekman流、地转流之和(c=e+g)。Ralph等(1999)指出在热带太平洋地转流和Ekman流对15 m处浮标流速的方差贡献率分别是63%和15%, 累计方差贡献率为78%, 证明了该假设在热带太平洋的合理性。许多反演海表流场的工作(Sudre, 2013; Hui, 2016)验证了该假设在全球的合理性。

GEKCO2数据基于Lagerloef等(1999)的方法反演海表流场, Hui等(2016)重新推导了该方法, 其表达形式为

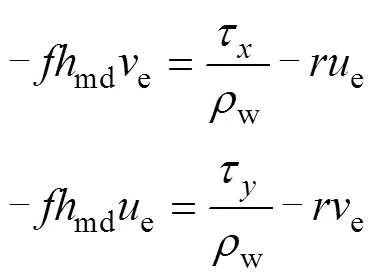
其中,轴分别以东、北为正方向,为科式参数,md为混合层深度,e(e,e)为海表Ekman流向量,(τ, τ)为海表风应力,w=1.02×103kg/m3为海水密度,为摩擦系数。为估算Ekman流, GEKCO2数据首先通过实测资料得到md和在不同海盆随纬度的变化关系, 然后将风场输入模型, 通过式(1)得到e。

由于GEKCO2数据存在数据缺失现象, 为了保证结果合理性, 本文选取数据缺失天数在50 d以内的南大洋海域作为数据有效区域(图1b的蓝色区域), 而舍弃了部分高纬度南大洋地区的数据(图1b的粉色区域)。

1.3 风场资料

由于测量设备、算法选择、数据质量以及观测实验等的不同, 各个风场数据之间存在一定区别。Schmidt等(2017)将南大洋实测数据与SW(SeaWinds)、ERA-Interim(ECMWF reanalysis interim)、NCEP-- DOE(National Centers for Environmental Prediction- department of energy)、CFSv2(NCEP version 2 coupled forecast system model)四个风场数据进行比较, 指出ERA-Interim数据最能代表风场的时间变化。Li等(2013)指出在南大洋, 相比于NCEP-DOE、ERA-Interim和NCDC(National Climatic Data Center), CCMP海表风速与船舶实测数据的误差最小。

为了避免只使用一个风场数据的片面性, 本文采用了RSS(remote sensing systems)发布的CCMP Version 2和ECMWF(European Centre for Medium- Range Weather Forecasts)发布的ERA5两种风场资料, 并将结果进行对比。CCMPV2数据网址为http://www. remss.com/measurements/ccmp/, 该数据是CCMP数据的改进, 融合了SSM/I(special sensor microwave imager)、SSMIS(special sensor microwave imager sounder)、QuikSCAT、ASCAT等微波辐射计和微波散射计采集到的海面风场数据。本文获取的CCMP数据(版本为L3.5 CCMP V2.0)为2010—2018年的海面10 m高的月平均风场数据, 空间范围为70.125°—29.875°S, 0.125°—359.875°E, 分辨率为0.25°×0.25°。

ERA5是第五代ECMWF再分析资料, 取代了ERA-Interim, 在以下网址中选取所需数据的类型、时间、变量以及区域来获取数据: https://cds.climate. copernicus.eu/cdsapp#!/search?type=dataset。本文获取的ERA5资料为2010—2018年的海面10 m高的月平均风场数据, 空间范围为70.25°—29.75°S, 0°—359.75°E, 分辨率为0.25°×0.25°。

1.4 南大洋浮标数据

为验证GEKCO2在南大洋区域的有效性, 本文采用美国伍兹霍尔海洋研究所OOI(the ocean observatories initiative, https://oceanobservatories.org/)的阿根廷锚系浮标阵列(Global Argentine Basin Array, 位置: 42.9204°S, 42.4409°W, 如图1a中的红色标记所示)和南大洋锚系浮标阵列(Global Southern Ocean Array, 位置: 54.0814°S, 89.6652°W, 如图1a中的紫色标记所示)所观测的风、流等变量对GEKCO2数据进行评估。风速数据由海表面浮标塔上的风速计进行测量, 并通过模型转换为海表面上方10 m风速值, 时间分辨率为1 h。海面下0—500 m处的流速数据由ADCP进行测量, 垂向深度分辨率为10 m, 时间分辨率为1 h(阿根廷锚系浮标阵列)或3 h(南大洋锚系浮标阵列)。此外, OOI通过Single Point Velocity Meter观测了海面下12 m处的流速, 时间分辨率为15 min。

2 结果及分析

2.1 南大洋浮标Ekman流提取及GEKCO2数据评估

随着观测技术的提高, 关于南大洋Ekman流的研究越来越受到重视。Ekman流速的量级一般为每秒几个厘米到每秒十几个厘米(Lenn, 2009)。Lenn等(2009)使用德雷克海峡的船载ADCP数据提取Ekman流, 提取结果显示深度26 m的Ekman流速为1.6 cm/s。Polton等(2013)的提取结果显示深度10 m处的Ekman流速为1.2 cm/s。

Roach等(2015)基于41°—49°S的EM-APEX浮标, 得到了1572个位置的流速剖面以及混合层深度, 通过提取近惯性流速, 并去除地转切变流和恒定地转参考流, 最终得到359个Ekman螺旋(垂向深度分辨率为2 m)。将这些Ekman螺旋的流速数据进行平均, 得到10、20、30 m处的平均流速分别为19.98、11.26、7.44 cm/s; 将混合层内的平均Ekman流速作为海表Ekman流速, 得到海表Ekman流速的均值为11.67 cm/s, 这与下文GEKCO2数据的平均Ekman流速9.918 cm/s相差不大。

本节选取了南大洋锚系浮标阵列从2017年4月15日0时到8月13日0时的风场数据(图2a)和流速数据, 其中ADCP测量的流速深度为16.47—506.47 m, Single Point Velocity Meter测量的流速深度为12 m。总流速total()包含近惯性流速ni()和潮流流速tidal(),ni()又由Ekman流速ek()和地转流速geo()两部分构成(Chereskin, 1995; Lenn, 2009; Roach, 2015; Liu, 2018), 其中为时间:

本文主要分析Ekman流速, 需要把其余两个流速滤除。为了滤除潮波信号, 保留近惯性频率信号, 本文采用Zhang等(2009)提及的希尔伯特变换(Hilbert transform)带通滤波方法。通过对滤波前流速信号的频谱分析, 本文将带通频段取为[0.92, 1.09], 海面下12 m处流速时间序列在滤波前后的频谱分析如图2b所示, 滤波前后的流速对比如图3a、3b所示(若选取时间过长会导致展示效果差, 因此只展示了4月15日0时到4月24日0时的时间序列)。由于地转流速经常随深度变化, 恒定地转流速的假设很可能导致一部分地转流速与Ekman流速发生混叠, Roach等(2015)提出, 将geo()分为恒定地转参考流速deep()和恒定地转切变流速[dgeo()d], 其中为水深且取轴垂直向上为正:

为了确定deep()和[dgeo()/d]的数值, 绘制了4月15日2时流速滤波后的剖面图, 见图2c。本文选取深度176.47—206.47 m之间的流速计算恒定地转参考流。根据Ralph等(1999)提出的Ekman深度计算公式:

图2 风速U10的时间序列图(a), 滤波前(红线)后(蓝线)流速频谱分析图(b)和去除地转流前后的流速剖面图(c, d)

图3 南大洋锚系浮标阵列水深12 m处滤波前后东向流速时间序列u (a)、北向流速时间序列v (b)以及东向Ekman流时间序列uek (c)、北向Ekman流时间序列vek (d)

其中, φ为流速数据的纬度, U10=10.58 m/s为海表面上10 m处的风速(上划线代表所取时间内的均值), 得到DE=83.53 m, 最接近采样深度86.47 m。因此, 选取86.47—176.47 m之间的流速计算切变地转流, 最终得到56.47—206.47 m处的Ekman流的垂向剖面如图2d所示。将地转切变和恒定地转参考流代入式(3)得到12 m处的地转流数据, 得到该处从2017年4月15日0时到8月13日0时的Ekman流, 如图3c、3d所示(同样只展示了4月15日0时到4月24日0时的时间序列)。利用相同的方法得到2016年3月14日0时到5月31日0时阿根廷锚系浮标阵列12 m处的Ekman流(图4)。本文将南大洋锚系浮标阵列和阿根廷锚系浮标阵列12 m处Ekman流速分别与GEKCO2同一地点数据进行对比(图5), 可以看出在两个浮标阵列处, 虽然12 m处Ekman流速变化幅度更大, 但其与GEKCO2数据随时间的变化趋势较为一致, 所以本文认为GEKCO2数据是合理有效的。

Fig.4 The time series of eastward Ekman current velocityek(a) and northward Ekman current velocityek(b) at 12 m in the Global Argentine Basin Array

图5 GEKCO2数据与12 m处Ekman流速对比

注: a: 南大洋锚系浮标阵列; b: 阿根廷锚系浮标阵列

2.2 Ekman流速的时空变化

2.2.1 Ekman流速的时间变化 图6展示了GEKCO2所提供的Ekman流速随时间的变化, 需要说明的是图6的所有数据建立在对Ekman流速进行空间平均的基础上。图6a—6c中红色虚线为2010—2018年年的平均Ekman流速, 为定值9.918 cm/s; 图6a中蓝色实线为2009年11月1日到2019年2月28日共3407 d的Ekman流速时间序列, 黄色实线是其经过滑动平均(窗口大小为101)后的时间序列。从滤波后的时间序列可以看出, Ekman流速存在周期变化, 且周期为1 a左右。为进一步分析Ekman流速的时间变化规律, 本文计算出2010—2018年流速的年平均值(图6b蓝色实线)和月平均值(图6c蓝色实线)。可以看出, 流速的年际变化很小, 最大值(2018年)和最小值(2016年)之差为0.08 cm/s, 仅为平均流速的0.8%; 与年际变化相反, Ekman流速具有很强的月际变化特征, 在6—8月(冬季)较大, 12—2月(夏季)较小, 最高值和最低值的差为1.3 cm/s, 接近平均流速的13.2%, 远远大于年际变化的0.8%, 由此可以说明Ekman流速的时间变化主要体现在月份上。

2.2.2 Ekman流速的空间变化 由图6a可知, Ekman流速在时间上表现出明显的年周期变化, 且不同月份的Ekman流速存在显著差异(图6c), 因此探究Ekman流速均值的空间分布时需要使用整年的数据。基于此原因, 本文使用了2010—2018年共9 a的数据, 而舍弃了非整年数据(2009年11、12月份及2019年1、2月份的数据, 会导致均值偏小)。南大洋区域Ekman流速均值的空间分布如图7a所示, 图中每个点的值为2010—2018年期间该点Ekman流速的时间均值。流速在10 cm/s以上的区域面积为6.78×1014km2, 占研究区域总面积的46%; 流速在11 cm/s以上的区域面积为3.69×1013km2, 占研究区域总面积的2.5%。40°—60°S纬度带的Ekman流速集中分布在10 cm/s以上, 尤其是30°—150°W区域(图7a黑框), 该区域是南大洋Ekman流最为强势的区域。图7c为由CCMP风场数据计算出的2010—2018年的风速均值, 可以看出风速较大区域(图7c黑框)的Ekman流速也较大, 因此Ekman流速的空间分布受风场的影响。同时, 由Ekman流速区间分布图(图8a)可见, 南大洋区域的Ekman流速主要分布在9—11 cm/s之间, 占总面积的91.8%。

南大洋区域Ekman流速标准差的空间分布如图7b所示, 该图描述了南大洋不同地区Ekman流速随时间的波动情况, 图中每个点的值为2010—2018年期间该点Ekman流速的标准差。可以看出, 南大洋Ekman流速标准差的地区分布差异比较大, 40°S以北海域流速随时间变化较大, 标准差基本在3 cm/s以上; 而40°—60°S, 0°—143°E地区(图7b黑框)的流速变化较小。图7d为由CCMP风场数据计算出的2010—2018年的风速标准差的空间分布, 与Ekman流速标准差的空间分布之间的差异较大, 说明除了风场, Ekman流速的时间变化还受其他因素的影响。

2010年1月到2018年12月期间Ekman流速区间分布的年际变化和月际变化分别如图8b、8c所示, 可以看出流速区间分布的月际变化特征强于年际变化特征。为进一步分析Ekman流速的月际变化, 本文将2010—2018年期间1、4、7、10月份的Ekman流速均值(图9a—9d)减去南大洋各点的总流速均值(图7a), 得到这4个月流速异常的空间分布(图9e—9h), 分别代表典型夏季、秋季、冬季、春季流速异常的空间分布特征。可以看出, 在夏季(冬季)南大洋Ekman流速呈整体性地减弱(增强), 对应后文经验正交函数分析(empirical orthogonal function, EOF)结果的第一模态。

图6 Ekman流速的时间序列(a)、随年份的变化(b)以及随月份的变化(c)

注: 所有Ekman流速数据建立在空间平均的基础上, 红色虚线为2010—2018年年的平均Ekman流速, 图6a中蓝色实线为2009年11月1日到2019年2月28日的Ekman流速时间序列, 黄色实线是其经过滑动平均(窗口大小为101)后的时间序列, 图6b蓝色实线为2010—2018年流速的年平均值, 图6c蓝色实线为2010—2018年流速的月平均值

图7 Ekman流速均值(a)和标准差(b)的空间分布, 风速均值(c)和标准差(d)的空间分布

注: 浅灰色为陆地, 白色为数据无效区域; 图7a黑色方框表示南大洋Ekman流最为强势的区域, 图7b黑色方框表示流速变化较小的区域, 图7c黑色方框表示南大洋风速较大区域

图8 Ekman流速的区间分布(a), Ekman流速区间分布的月际变化(b)和年际变化(c)

2.2.3 基于EOF的Ekman流速变化特征分析 本节采用EOF方法对研究区域2010—2018年的再分析Ekman流速进行分析。EOF分析本质上是一种主成分分析方法, 能够提取数据的主要特征量, 目前在海洋科学以及地球科学领域发挥着巨大的作用。杨洋等(2018)采用EOF方法分析东中国海海平面高度的时空变化; 潘卫华等(2019)分析了台湾海峡海面风场的时空变化; 罗凤云等(2020)采用季节EOF分析南海海平面异常在中部、东部型El Niño期间的时空演变特征; 韩树宗等(2020)用其分析南海波浪波高的时空变化; 秦岭等(2020)分析全球春-秋季风降水强度的年际变化。

本节首先对2010—2018年每个空间点上的Ekman流振幅进行逐月平均, 并进行距平处理, 然后利用EOF方法进行分析, 并进行显著性检验。表1给出各个模态的方差贡献率, 可以看出, 前两个模态累计方差贡献率为45%, 且通过North检验, 因此前两个模态可以较好地解释2010—2018年南大洋Ekman流速的空间变化特征。模态空间场上某个点的绝对值越大, 则该点的Ekman流速变化越显著; 相反, 如果该点的绝对值越接近零, 则该点的Ekman流速在时间上的变化越趋于稳定。

第一模态(图10a)的方差贡献率为37.7%, 可以表征南大洋海域Ekman流速的主要空间分布特征。除了在少部分海域(如南非西边海域、澳大利亚西边海域, 南美洲35°S西边海域等), 第一模态均为负值, 表明2010—2018年期间Ekman流速在整体上同时增强或减弱的分布特征; 第一模态在40°S以北海域的绝对值较大, 对应图7b流速标准差较大处; 以(35°S, 89°E)、(33.5°S, 101°W)和(31.5°S, 6°W)为中心的三个区域出现了第一模态的极小值, 说明这三个区域的月际变化强烈; 以(48°S, 110°E)和(50°S, 100°W)为中心的两个区域的模态接近零, 表明其月际变化比较平稳。第二模态如图10b所示, 以50°S为界, 基本将南大洋海域从南北两向分为负值区和正值区, 该模态代表Ekman流速在南北方向上反向变化的分布特征。

图9 Ekman流速(a—d)在1、4、7、10月份的空间分布及异常流速(e—h)在1、4、7、10月份的空间分布

注: 浅灰色为陆地, 深灰色为数据无效区域

表1 Ekman流速EOF分析的前五个模态

Tab.1 The First Five Modes of EOF Analysis of the Speed of Ekman Current

图10 Ekman流速的EOF分析中的前两个模态

注: a: 第一模态, b: 第二模态

图11a、11b的蓝线分别为第一、二模态所对应的时间系数。时间系数表示这一区域由特征向量所表征的模态的时间变化特征, 该时刻模态是否典型与对应时间系数数值绝对值大小成正比。第一模态时间系数表明南大洋Ekman流速具有很强的月际变化, 这与之前得到的结论相同; 将南大洋研究区域CCMP风速数据进行月平均及空间平均, 得到的结果为研究区域的风速指标(图11a橙线)。该指标与第一模态时间系数的相关性系数为-0.62, 呈负相关, 且通过0.01的显著性检验, 因此Ekman流速第一模态和风场之间存在较强的相关性。

Gong等(1999)研究了南极涛动(Antarctic oscillation, AAO), 并定义了南极涛动指数。南极涛动是南半球热带外地区最显著的半球尺度大气活动模态(Thompson, 2000), 具有以位于极区(60°S以南)与环绕极区(45°S)的位势高度场异常反向变化的特点(宋洁等, 2009), 且对南半球的海洋风场、温度场都有一定的影响(Lovenduski, 2005)。本文使用的AAO指数数据(图11b橙线)来自于NOAA(National Oceanic and Atmospheric Administration), 它是对20°S以南的NCEP/NCAR再分析月平均海平面气压距平场(1979年1月到2020年10月)进行EOF分解得到的第一模态时间系数。AAO指标与第二模态时间系数的相关性系数为-0.64, 呈负相关, 且通过0.01的显著性检验。同时, 南大洋Ekman流速第二模态与南极涛动模态都具有中高纬度反向变化的空间分布特征。因此第二模态和南半球中高纬大气环流之间存在较强的相关性, 本文猜测中高纬大气环流通过风场、温度场等影响Ekman动力过程。结合2.2.2节, 本文认为南大洋Ekman流速的时空分布特征主要受风场以及南半球中高纬大气环流的影响。

2.3 Ekman流左偏角度的时空变化

2.3.1 Ekman流左偏角度的时间变化 根据经典Ekman漂流理论, 南半球Ekman流偏向风矢量的左边。本文定义两者偏角为Ekman流偏离风矢量的角度(逆时针为正, 即左偏)。图12e为Ekman流和风矢量偏角的概率分布, 可以看出, 虽然Ekman流场和ERA5风场的夹角概率分布相对于CCMP风场而言比较“平缓”, 但是两者得到的偏角都集中在60°—75°, 概率密度最大值处所对应的角度也都为67.5°。图12a和12b为Ekman流和风矢量偏角在不同年份的概率分布图, 偏角分布随年份的变化程度很小。图12c和12d为Ekman流和风矢量偏角在不同月份的概率分布图, 在流速较大的七月, 无论是使用CCMP还是ERA5风场, 偏角分布程度较其他月份都有变化, 但相差不大。

2.3.2 Ekman流左偏角度的空间变化 从图12f可以看出, 除30°S附近, 使用ERA5风场时的纬向平均偏角大于CCMP风场, 但是两者随纬度的变化情况较为一致, 在35°S都有明显的变小。从图13可以看出, 使用CCMP和ERA5风场得到的偏角空间分布图很相似, 35°—70°S之间的高纬区域的偏角在65°—70°之间; 30°—35°S之间的区域出现了少数偏角小于零的情况(即偏向风的右侧), 以及部分偏角大于90°的区域。

图11 第一模态时间系数及风速指标时间序列(a), 第二模态时间系数及南极涛动指数(b)

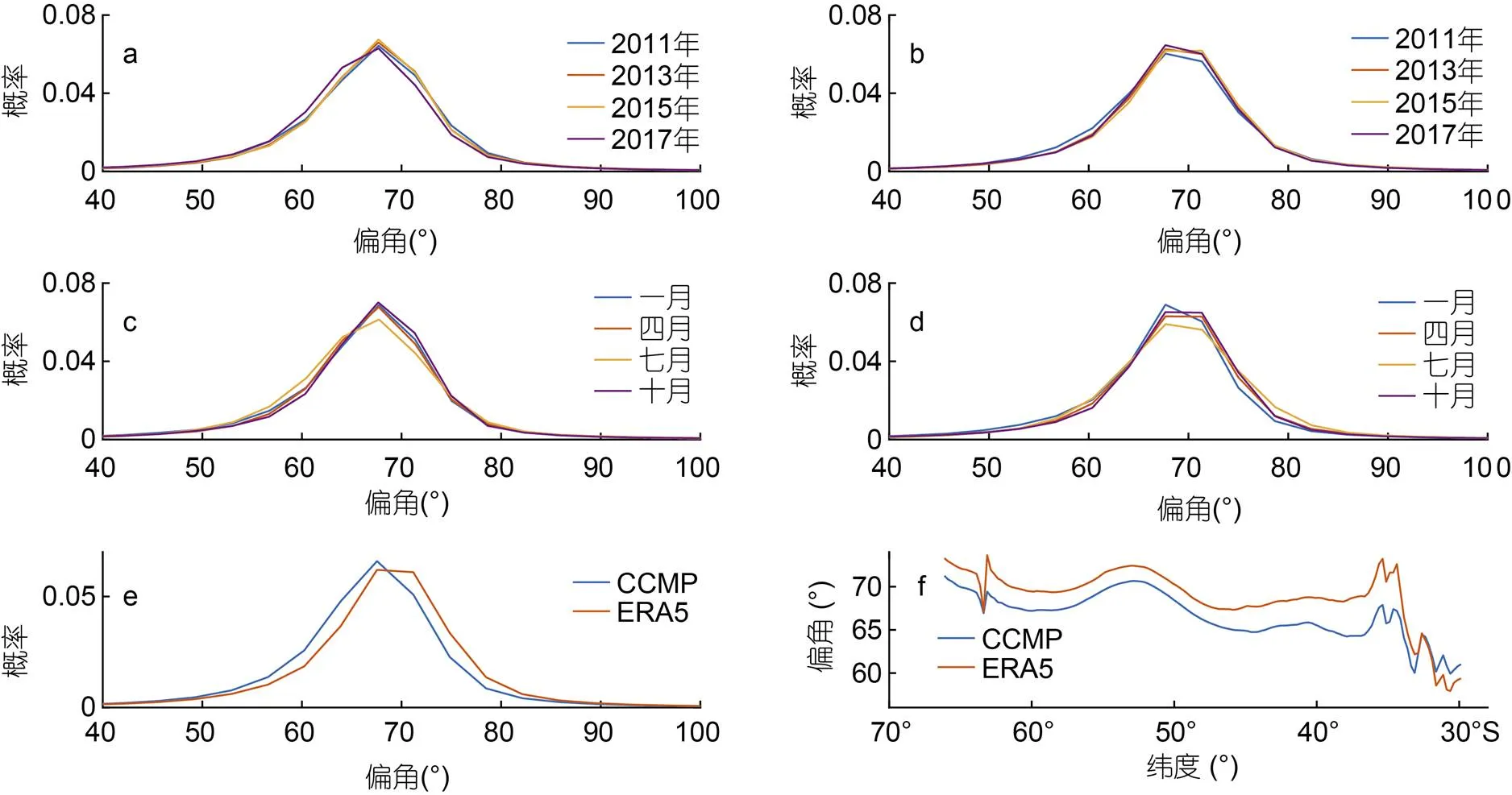
图12 Ekman流偏角在不同年份的概率分布(a, b), Ekman流偏角在不同月份的概率分布(c, d), Ekman流左偏角的概率分布(e), Ekman流偏角随纬度的变化(f)

注: a和c的风场资料为CCMP, b和d的风场资料为ERA5

图13 南大洋Ekman流时间平均偏角的空间分布图

注: a的风场资料为CCMP, b的风场资料为ERA5

2.3.3 风场与Ekman流场之间的矢量相关 由于CCMP和ERA5风场的区别不大, 因此只使用CCMP数据来探究风场和Ekman流场之间的矢量相关。从图13可以看出, 南大洋30°—35°S之间区域的Ekman流偏角情况较为复杂, 同时考虑到不同月份的偏角存在差异, 因此本文以35°S为界将南大洋分为上下两部分, 探讨这两片海域以及南大洋整个海域的Ekman流场在不同月份与CCMP风场的矢量相关(见附录)。如图14b所示, 计算得到的||(衡量两个随时间变化的矢量之间的相关性)都在0.84以上, 因此本文认为得到的θ(两个随时间变化的矢量的夹角)都是合理的。如图14a所示, 30°—35°S海域的Ekman流偏角存在月际变化, 4月份和9月份之间的偏角相差7°; 不同于该片海域, 35°—70°S海域的Ekman流偏角稳定在67.5°附近, 30°—70°S海域(即南大洋整个海域)的Ekman流偏角稳定在67°附近。

图14 南大洋不同海域的Ekman流场在不同月份与CCMP风场的矢量相关

注:表示矢量相关;θ表示两个随时间变化的矢量的夹角

3 结论

本文在验证GEKCO2数据有效性的基础上, 采用GEKCO2数据探讨2010—2018年期间Ekman流速在南大洋区域的时空分布特征。通过对Ekman流速时间序列的分析, 发现其集中在9—11 cm/s, 且具有很强的月际变化特征。为研究Ekman流速在不同区域的差异性, 本文给出了南大洋各个点的流速均值及标准差, 流速高值区域为40°—60°S, 30°—150°W, 而40°S以北海域是Ekman流速随时间变化较大的区域。为进一步分析南大洋Ekman流速的时空变化规律, 本文对2010—2018年逐月平均Ekman流速进行EOF分析。第一模态表现为流速在整体上同时增强或减弱的分布特征, 第二模态表现为以50°S为界流速南北反向变化的分布特征; 同时通过时间系数与气候指标的相关性分析, 发现第一模态和风场之间存在较强的相关性, 第二模态和南半球中高纬大气环流存在较强的相关性。结合CCMP、ERA5风场资料, 本文继续讨论了Ekman流偏向角度的时空变化特征。Ekman流左偏角度集中在60°—75°, 其中概率密度最大值处所对应的角度为67.5°。Ekman流左偏角度随时间的变化很小, 随着纬度的变小左偏角度也在变小。通过矢量相关分析, 得到30°—35°S海域的平均偏角存在月际变化, 其中4月和9月之间的偏角相差7°。

本文的研究结论对于进一步理解南大洋的Ekman过程具有一定的参考价值。虽然本文充分调研了关于南大洋Ekman流的文献资料, 并利用Roach等(2015)的实测资料和伍兹霍尔海洋研究所的两个南大洋浮标数据, 对再分析数据Ekman流速进行了评估; 但受限于南大洋区域的观测难度, 实测资料的时空分布密度较低, 故本文对于再分析数据的验证仍然不够充分, 这一点将在未来的工作中通过数值模式予以弥补。

附录: 矢量相关

Kundu(1976)提出了矢量相关(complex correlation), 用来计算两个随时间变化的二维速度矢量之间的平均夹角, 也可用来衡量模型结果和观测数据之间的匹配程度(Yin, 2007)。假设二维速度矢量为

()=()+(), (5)

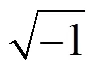
其中, 星号表示复数共轭, 尖括号表示时间平均, 也可写为

因此,

需要注意的是只有当||较大时,θ才有意义。

史久新, 2000. 南大洋印度扇形区南极绕极流和南极沿岸流的相互作用研究. 中国科学院海洋研究所博士学位论文, 1—6

刘 巍, 张 韧, 王辉赞等, 2012. 基于卫星遥感资料的海洋表层流场反演与估算. 地球物理学进展, 27(5): 1989—1994

安玉柱, 张 韧, 王辉赞等, 2012. 基于卫星遥感数据的全球表层流场反演重构. 海洋通报, 31(1): 1—8

杨 洋, 孙 群, 杨 敏等, 2018. 东中国海海平面高度的时空变化特征. 海洋与湖沼, 49(3): 481—489

宋 洁, 李崇银, 2009. 南极涛动和北半球大气环流异常的联系. 大气科学, 33(4): 847—858

罗凤云, 谭 伟, 李 娟等, 2020. 南海海平面对两类El Niño的不同响应. 海洋学报, 42(3): 36—46

秦 岭, 黄 菲, 许士斌等, 2020. 全球春-秋季风降水的年际变化主模态时空特征. 中国海洋大学学报(自然科学版), 50(10): 11—18

韩树宗, 董杨杨, 张水平等, 2020. 南海波浪时空变化特征研究. 海洋湖沼通报, (2):1—9

潘卫华, 林 毅, 2019. 近10年台湾海峡海面风场的时空特征变化动态分析. 热带气象学报, 35(3): 296—303

Bonjean F, Lagerloef G S E, 2002. Diagnostic model and analysis of the surface currents in the tropical Pacific Ocean. Journal of Physical Oceanography, 32(10): 2938—2954

Chereskin T K, 1995. Direct evidence for an Ekman balance in the California Current. Journal of Geophysical Research: Oceans, 100(C9): 18261—18269

Constantin A, 2021. Frictional effects in wind-driven ocean currents. Geophysical & Astrophysical Fluid Dynamics, 115(1): 1—14

Constantin A, Johnson R S, 2019. Ekman-type solutions for shallow-water flows on a rotating sphere: A new perspective on a classical problem. Physics of Fluids, 31(2): 021401

Cronin M F, Kessler W S, 2009. Near-surface shear flow in the tropical pacific cold tongue front. Journal of Physical Oceanography, 39(5): 1200—1215

Ekman V W, 1905. On the influence of the Earth’s rotation on ocean-currents. Arkiv för Matematik, Astronomi Och Fysik, 2(11): 1—52

Elipot S, Gille S T, 2009. Ekman layers in the Southern Ocean: spectral models and observations, vertical viscosity and boundary layer depth. Ocean Science, 5(2): 115—139

Gong D Y, Wang S W, 1999. Definition of Antarctic Oscillation index. Geophysical Research Letters, 26(4): 459—462

Hui Z L, Xu Y S, 2016. The impact of wave-induced Coriolis-Stokes forcing on satellite-derived ocean surface currents. Journal of Geophysical Research: Oceans, 121(1): 410—426

Kundu P K, 1976. Ekman veering observed near the ocean bottom. Journal of Physical Oceanography, 6(2): 238—242

Lagerloef G S E, Mitchum G T, Lukas R B, 1999. Tropical Pacific near-surface currents estimated from altimeter, wind, and drifter data. Journal of Geophysical Research: Oceans, 104(C10): 23313—23326

Lenn Y D, Chereskin T K, 2009. Observations of Ekman currents in the Southern Ocean. Journal of Physical Oceanography, 39(3): 768—779

Li M, Liu J P, Wang Z Z, 2013. Assessment of sea surface wind from NWP reanalyses and satellites in the Southern Ocean. Journal of Atmospheric and Oceanic Technology, 30(8): 1842—1853

Liu J, Dai J J, Xu D F, 2018. Seasonal and interannual variability in coastal circulations in the northern South China Sea. Water, 10(4): 520

Lovenduski N S, Gruber N, 2005. Impact of the Southern Annular Mode on Southern Ocean circulation and biology. Geophysical Research Letters, 32(11): L11603

McWilliams J C, Huckle E, 2006. Ekman layer rectification. Journal of Physical Oceanography, 36(8): 1646—1659

Nowlin W D Jr, Klinck J M, 1986. The physics of the Antarctic Circumpolar Current. Reviews of Geophysics, 24(3): 469—491

Polton J A, Lenn Y D, Elipot S, 2013. Can drake passage observations match Ekman’s classic theory?. Journal of Physical Oceanography, 43(8): 1733—1740

Ralph E A, Niiler P P, 1999. Wind-driven currents in the Tropical Pacific. Journal of Physical Oceanography, 29(9): 2121—2129

Roach C J, Phillips H E, Bindoff N L, 2015. Detecting and characterizing Ekman currents in the southern Ocean. Journal of Physical Oceanography, 45(5): 1205—1223

Schmidt K M, Swart S, Reason C, 2017. Evaluation of satellite and reanalysis wind products with in situ wave glider wind observations in the Southern Ocean. Journal of Atmospheric and Oceanic Technology, 34(12): 2551–2568

Speer K, Rintoul S R, Sloyan B, 2000. The diabatic deacon cell. Journal of Physical Oceanography, 30(12): 3212—3222

Sudre J, Maes C, Garçon V, 2013. On the global estimates of geostrophic and Ekman surface currents. Limnology & Oceanography Fluids & Environments, 3(1): 1—20

Thompson D W J, Wallace J M, 2000. Annular modes in the extratropical circulation. Part I: Month-to-month variability. Journal of Climate, 13(5): 1000—1016

Wenegrat J O, McPhaden M J, 2016. Wind, waves, and fronts: Frictional effects in a generalized Ekman model. Journal of Physical Oceanography, 46(2): 371—394

Yin X Q, Oey L Y, 2007. Bred-ensemble ocean forecast of loop current and rings. Ocean Modelling, 17(4): 300—326

Zhang J C, Li G Q, Yi J C, 2019a. A Method on estimating time-varying vertical eddy viscosity for an Ekman layer model with data assimilation. Journal of Atmospheric and Oceanic Technology, 36(9): 1789—1812

Zhang Y M, Song Z Y, Wu K J, 2019b. Influences of random surface waves on the estimates of wind energy input to the Ekman layer in the Antarctic circumpolar current region. Journal of Geophysical Research: Oceans, 124(5): 3393—3410

Zhang Y W, Tian J W, Xie L L, 2009. Estimation of eddy viscosity on the South China Sea shelf with adjoint assimilation method. Acta Oceanologica Sinica, 28(5): 9—16

THE SPATIAL AND TEMPORAL DISTRIBUTION OF EKMAN CURRENT IN THE SOUTHERN OCEAN BASED ON REANALYSIS DATA

LIN Hui-Yi1, GAO Yan-Qiu2, ZHANG Ji-Cai1

(1. Institute of physical oceanography and remote sensing, Ocean College, Zhejiang University, Zhoushan 316021, China;2. State Key Laboratory of Satellite Ocean Environment Dynamics, Second Institute of Oceanography, Ministry of Natural Resource, Hangzhou 310012, China)

Ekman transport in the Southern Ocean is an important part of the global atmosphere ocean coupled climate system. It is very important to study the Ekman dynamic process in this region. The Ekman current data provided by GEKCO2 product was evaluated and its validity verified. In addition, combined with sea surface wind products (CCMP and ERA5), EOF analysis and other methods were used to analyze the spatial and temporal variation of Ekman current in the Southern Ocean from 2010 to 2018. Results show that first, the speed of Ekman current ranged 9—11 cm/s with a strong inter-monthly oscillation (the strongest in July and the weakest in December). Secondly, the speed of Ekman current varied greatly with time north of 40°S in the Southern Ocean. Thirdly, The EOF analysis of the speed of Ekman current indicates that the first mode had a strong correlation with the wind field, in which the speed increased or decreased at the same time on the whole. The second mode had a strong correlation with the middle and high latitude atmospheric circulation in the southern hemisphere, in which the speed from north to south was reversed with 50°S as the boundary. Fourthly, the left deviation angle of Ekman current was distributed in the range of 60° to 75° with the maximum probability density at 67.5°. Through the analysis of complex correlation, it was found that the average deviation angle in the area of 30—35°S varied monthly. This study provides a reference for further understanding of the Ekman process in the Southern Ocean.

the Southern Ocean; Ekman current; spatial and temporal variation; empirical orthogonal function (EOF) analysis; ocean current product GEKCO2 (Geostrophic and Ekman Current Observatory 2)

* 国家重点研发计划“全球变化及应对”重点专项, 2017YFA0604100号; 国家重点研发计划“海洋环境安全保障”重点专项, 2017YFC1404000号; 国家自然科学基金, 41876086号; 国家自然科学基金, 41706006号。林辉义, 硕士研究生, E-mail: 21934005@zju.edu.cn

张继才, 副教授, 博士生导师, E-mail: jicai_zhang@163.com

2021-01-11,

2021-03-04

P731

10.11693/hyhz20210100010