±800 kV直流输电线路重冰区导、地线脱冰冲击敏感因素浅析
2021-07-21刘翔云何松洋宋玲林
刘翔云,何松洋,黄 兴,宋玲林
(中国电力工程顾问集团西南电力设计院有限公司,四川 成都 610021)
0 引 言
冰灾一直是威胁中国电网安全运行最为严重的自然灾害之一,一旦发生,可能引起输电线路倒塌产生大面积停电,给国民生活造成巨大影响。灾后调查报告显示,倒塌的输电铁塔中90%是由于不均匀覆冰和不均匀脱冰的不平衡张力造成的。对于±800 kV特高压直流输电线路,由于输送距离长,途经重覆冰区较多,其脱冰不平衡张力对于线路的安全运行存在较大的威胁。
架空输电线路导线和地线在脱冰时,其张力会发生突然变化,由于非平衡力的出现,会对杆塔产生不可忽视的冲击作用,冲击力的大小与线路的结构、覆冰以及脱冰有关,因而有必要研究在不同线路结构和覆冰厚度条件下,导线和地线脱冰产生的冲击作用。目前,学者们对线路脱冰的影响已经做了一些研究,主要集中在脱冰振动响应分析[1-4]和脱冰不平衡张力计算[5-7]等方面。目前关于脱冰的冲击作用研究较少,相关设计规范[8-10]也没有具体要求,脱冰冲击作为一种偶然荷载,对线路的影响不可忽略,因此有必要对脱冰冲击荷载展开研究。
1 脱冰数值计算理论
在计算导地线覆冰后的平衡状态时,可以通过等效密度来模拟导地线的载荷。覆冰后导地线的等效密度可由式(1)计算。
(1)
式中:ρe为覆冰后导、地线的等效密度;W1和W2分别为单位长度导、地线的自重和覆冰重量;A为其截面积。
在进行脱冰荷载计算时,假定脱冰率为β,则脱冰后残留在单位长度导、地线上的覆冰重量为W2(1-β),脱冰后导、地线的等效密度为
(2)
导线脱冰前的等效密度可以分解为两部分:
(3)
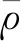
脱冰前导、地线运动惯性力可以分解为两部分:
(4)
由于假定脱冰前后导、地线的惯性力保持不变,脱冰后的惯性力按照式(5)计算。
(5)
结合式(2)至式(5)可以得到脱冰后的等效重力加速度为
(6)
式中,g′为脱冰后导、地线的等效重力加速度。
2 模型建立
为了研究导线和地线脱冰对杆塔的冲击作用,采用有限元方法研究不同线路结构、覆冰厚度和脱冰条件下导线脱冰时对绝缘子串挂点的冲击作用。±800 kV特高压直流线路采用LGJ-1250/100六分裂导线,地线为GJ-150,参数见表1。
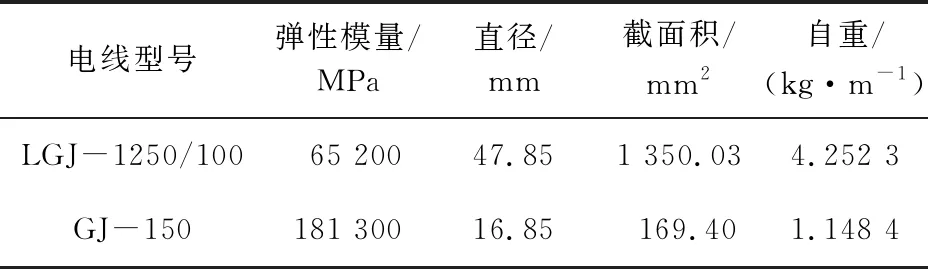
表1 ±800 kV六分裂导线和地线参数
其中,导线与直线塔连接的悬垂绝缘子串采用V型绝缘子串,其肢长为17.32 m,V串夹角为75°,总质量为5850 kg。导线与耐张塔连接采用双联耐张绝缘子串,长度为17.32 m,质量为11 130 kg。地线与直线塔连接的悬垂绝缘子串为I型双联悬垂绝缘子串,长度为1.00 m,重量为36.40 kg。地线与耐张杆塔连接采用双联耐张绝缘子串,其长度为6.31 m,重455.66 kg。
地线为I型绝缘子串模型时,导线为V型绝缘子串,绝缘子串的弹性模量和泊松比分别取为2.0×105MPa和0.3,采用理想弹塑性模型。绝缘子串的数值模型见图1所示。

图1 绝缘子串有限元模型
各线路段有限元模型两端均为耐张绝缘子串,耐张绝缘子串一端与导线连接,另一端为固定约束。V型悬垂绝缘子串上端的两个悬挂点采用线位移约束,但可以绕Z轴转动。导线和绝缘子串均采用空间梁单元模拟。
档距L和高差H的组合如表2所示。覆冰厚度分别为20 mm、30 mm;脱冰率均取100%。

表2 ±800 kV六分裂线路档距和高差组合
±800 kV六分裂线路导线安装的初始应力见表3。

表3 ±800 kV六分裂线路导线安装的初始应力
以连续三档脱冰对绝缘子的冲击为研究对象,详细分析了脱冰对V型串、I型串的冲击效应,连续三档导线模型见图2所示。
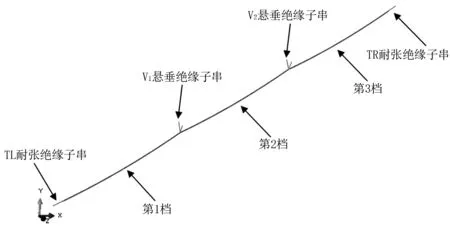
图2 ±800 kV连续三档导线模型
3 参数分析
针对建立的有限元模型,研究不同档数、不同档距和高差组合时,各档导地线分别脱冰时对悬垂绝缘子串和耐张绝缘子串挂点的冲击效应。通过对导线脱冰过程的数值模拟,对比分析V型悬垂绝缘子和耐张绝缘子串挂点在导线脱冰前的反力和导线脱冰过程中的反力,得到脱冰效应的控制因素。
如图3所示,导线在XY平面内。FH表示作用于绝缘子串挂点水平方向(X方向)的分力,FV表示作用于绝缘子串挂点垂直方向(Y方向)分力。
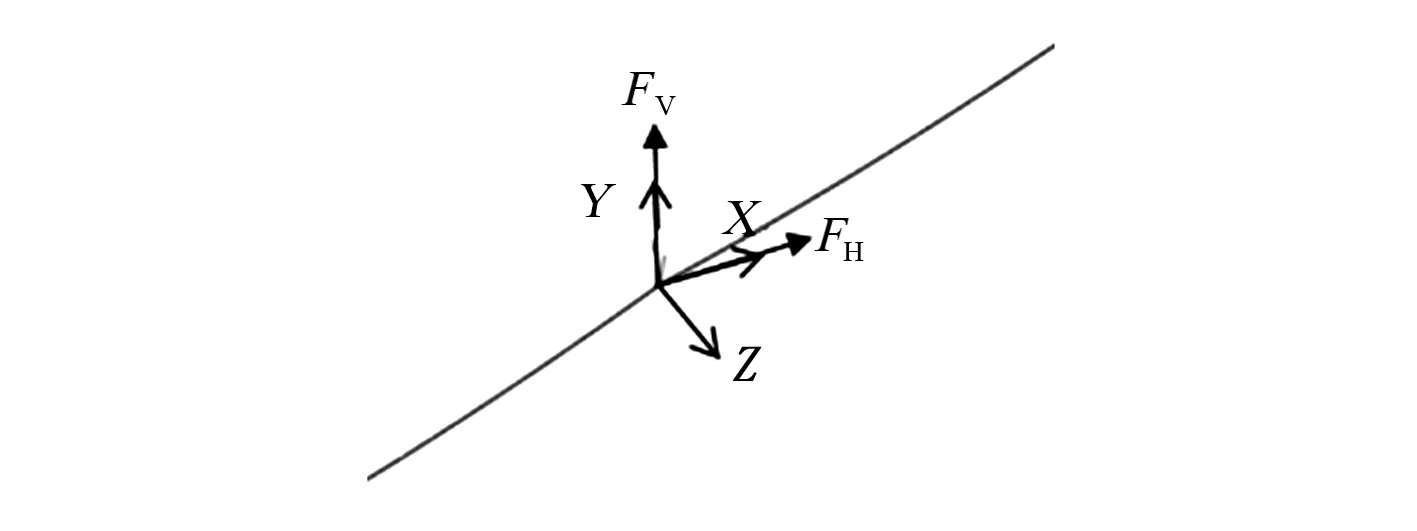
图3 作用于悬垂绝缘子串和耐张绝缘子串点的反力
3.1 导线脱冰对V型串的冲击作用
数值模拟研究表明,当档距为800 m、高差为400 m、第3档脱冰时,图2中V2串的冲击效应最大。V2串水平和垂直冲击力随档距和高差的变化如图4所示。
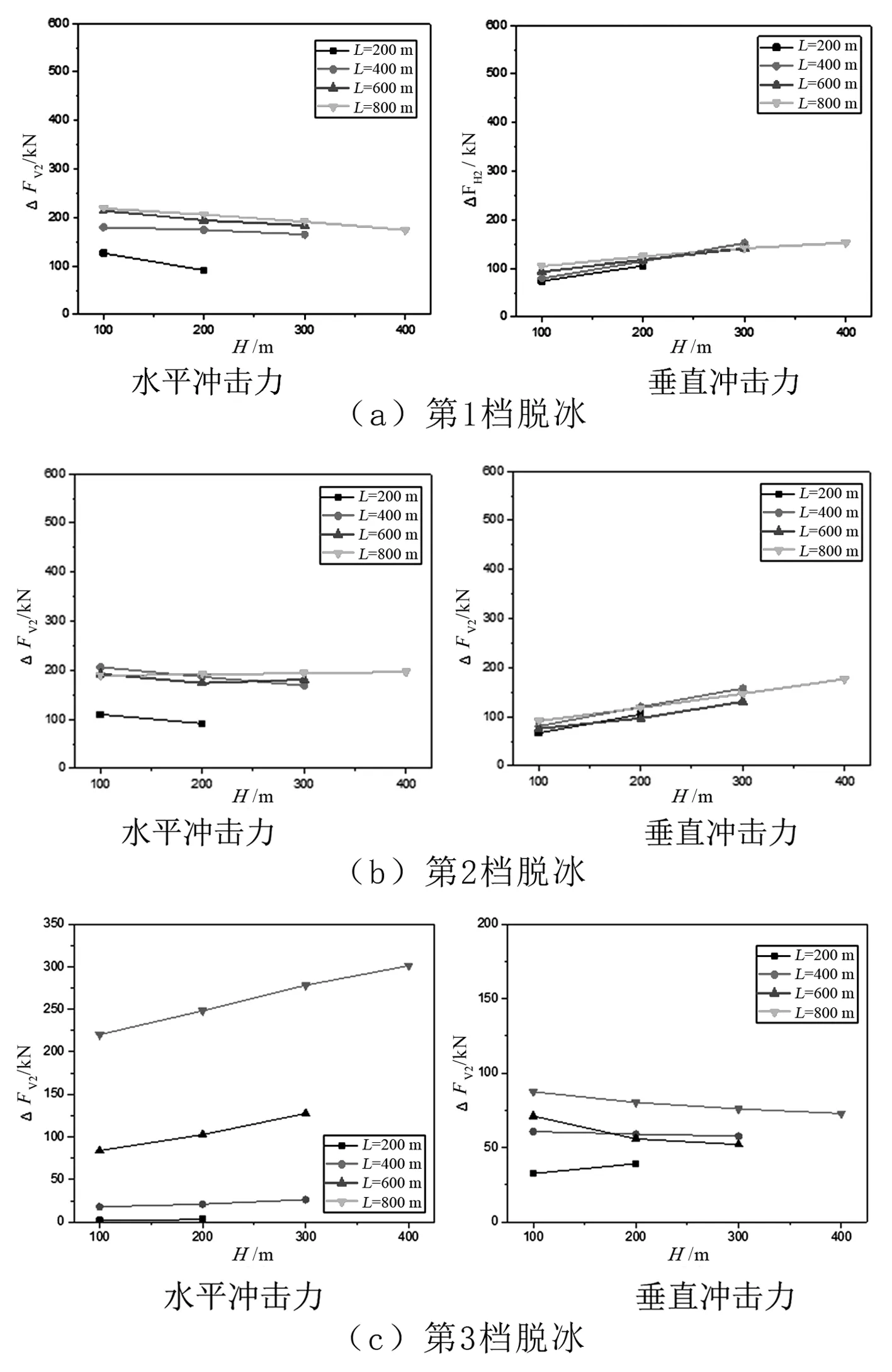
图4 各档脱冰V2串水平和垂直冲击力随高差的变化
图4表明,第3档脱冰时对V串的水平冲击效应较第1档和第2档分别脱冰时的大;在第2档脱冰时, V串挂点的垂直冲击效应最大。
3.2 导线脱冰对耐张串的冲击作用
数值模拟研究表明,当档距为800 m、高差为400 m、第3档脱冰时,作用于图2中TR耐张串上的水平冲击力最大,为581.94 kN;此时,作用于TR耐张串上的垂直冲击力也最大,为550.46 kN;合力的最大变化值为800.34 kN。
各档脱冰对TR耐张串水平和垂直冲击力随档距和高差的变化如图5所示。
图5表明,导线脱冰时,TR耐张串水平冲击载荷会随着档距的增大而增大,但受高差的影响不大;垂直冲击载荷会随着档距的增大而增大,也随高差的增大而增大。
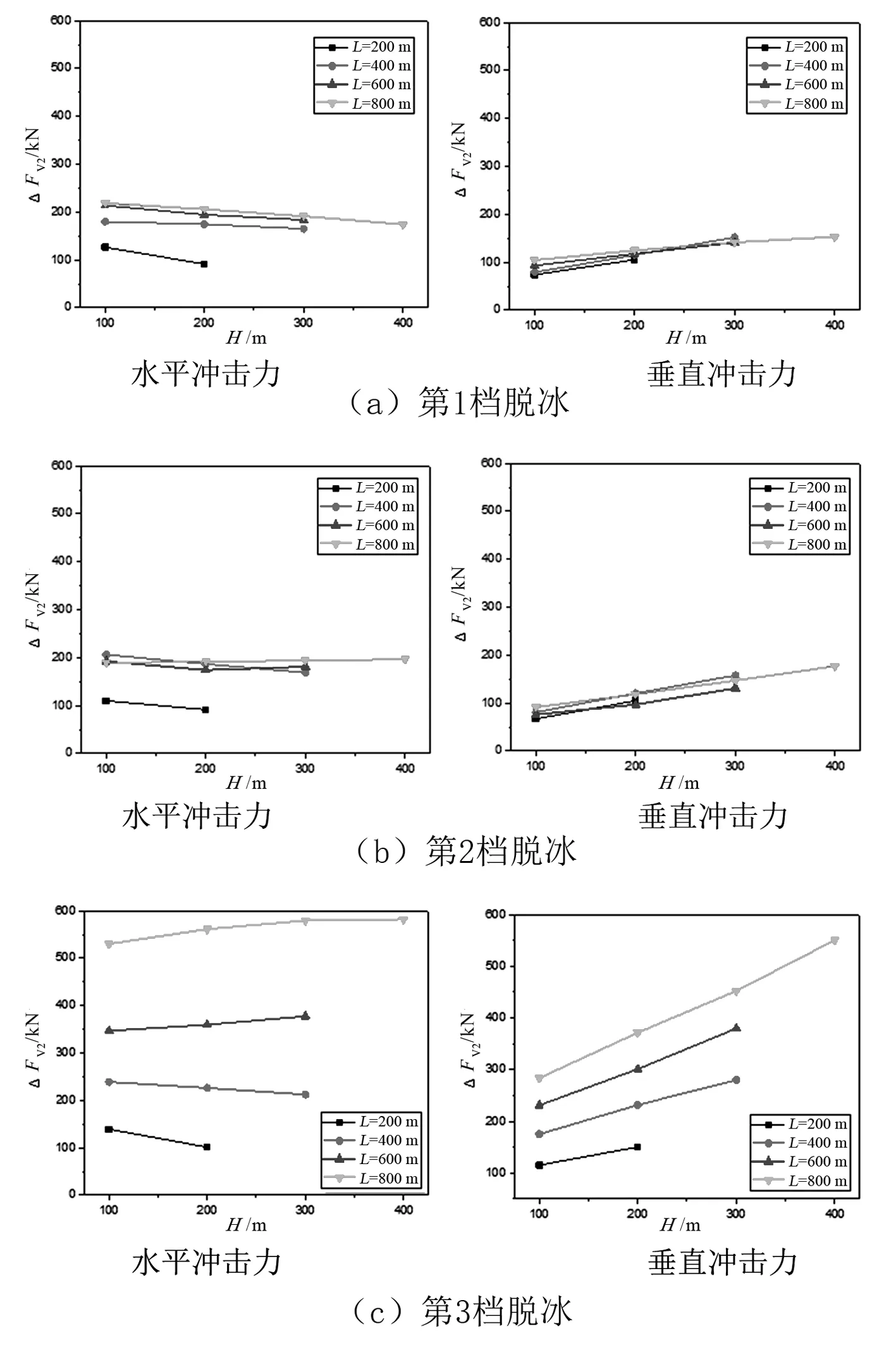
图5 各档脱冰TR耐张串水平和垂直冲击力随高差的变化
3.3 导线模态分析
模拟分析了典型三档六分裂导线覆冰模型的固有频率和模态。模型见图2,模型各档档距为800 m,高差为100 m,覆冰厚度为30 mm。覆冰导线的其他物理参数见表1。
计算得到线路模型的前10阶固有频率见表4。
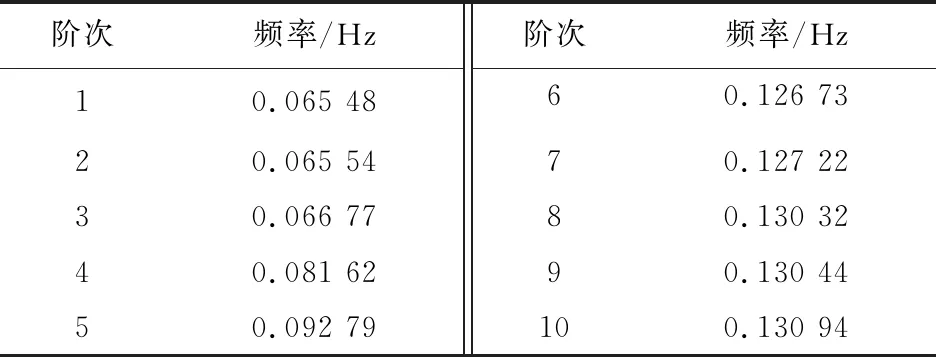
表4 连续三档低阶固有频率
前4阶模态变形云图如图6所示。
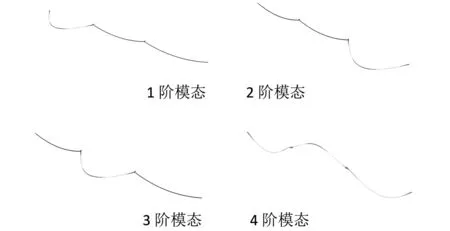
图6 模态云图
图6表明,连续三档导线模型的模态以单档局部水平挠曲变形为主,四阶模态发展为竖向挠曲变形。
分析连续三档六分裂导线脱冰后的振动模式时,对其典型位置(第2档中点)的位移时程响应进行频谱分析。第2档脱冰时其导线中点的垂直位移时程曲线如图7所示,频谱见图8。
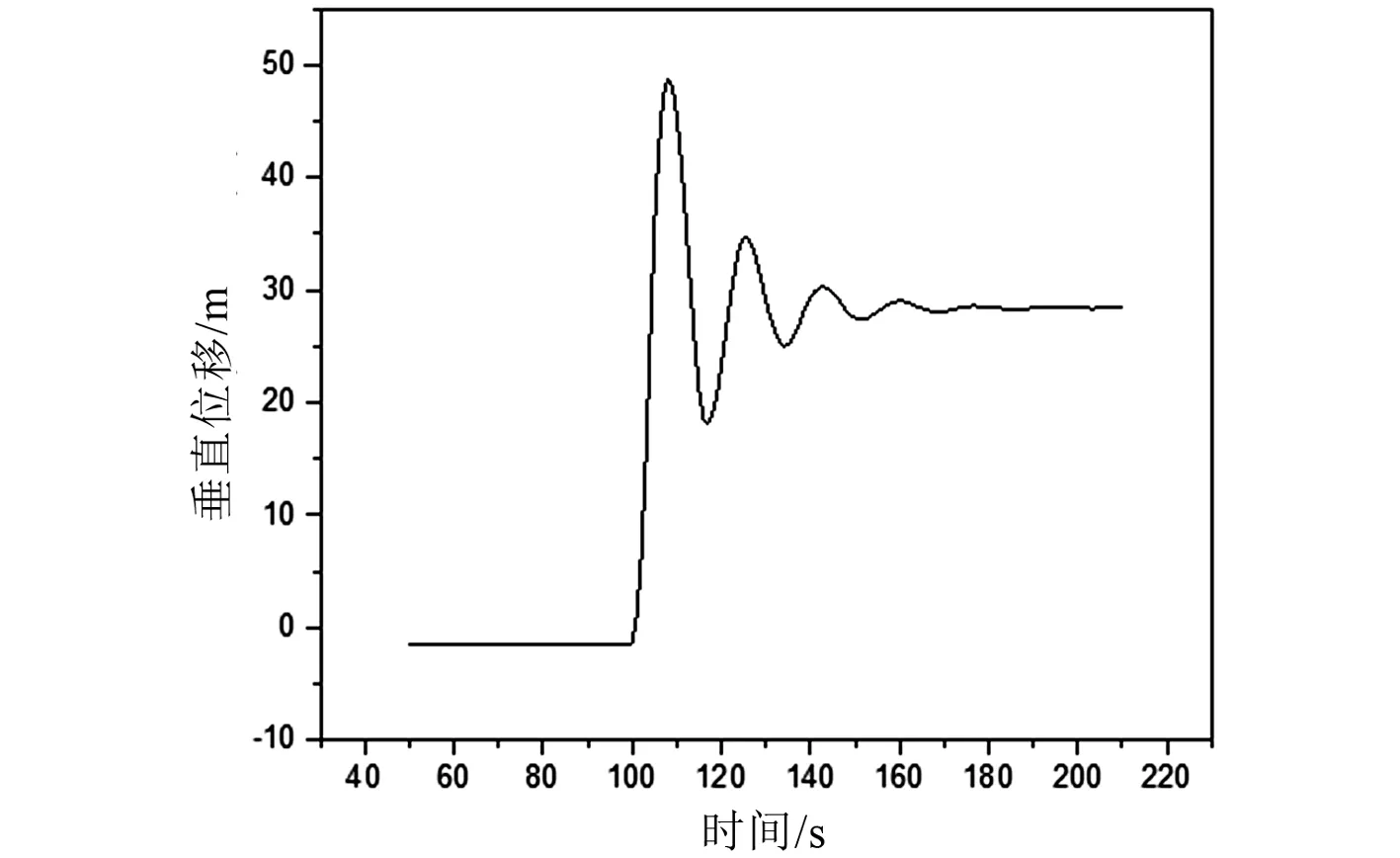
图7 第2档脱冰时导线中点垂直位移时程曲线

图8 第2档脱冰时导线中点的位移频谱
由图8可知,第2档脱冰时频率为0.068 9 Hz,接近于其三阶固有频率0.066 77 Hz,该固有频率对应的振动模态为单半波,即脱冰时导线的主振动为单半波形。
4 地线脱冰冲击参数分析
输电线路不同结构参数和脱冰参数条件下,地线脱冰对杆塔的冲击作用不同。以连续三档模型进行数值分析,导线V串处的地线采用I串,地线选用GJ-150,覆冰厚度30 mm,脱冰率为100%。不同档距下地线安装的初始应力见表5。

表5 GJ-150地线不同档距安装的初始应力
4.1 地线脱冰对I型串的冲击作用
研究表明:当档距为800 m、第2档地线脱冰时,地线I串的水平冲击效应最大,图2中V2串处地线绝缘子I2串上的最大水平冲击力为87.87 kN;当档距800 m、高差为400 m、第2档脱冰时,I串的垂直冲击效应最大, I2串上的最大垂直冲击力为64.16 kN。
各档脱冰时I2串垂直冲击力随档距和高差的变化如图9所示。

图9 各档脱冰I2串垂直冲击力随高差的变化
图9表明,不同档距条件下,高差越大,I2串垂直冲击力就越大。
4.2 地线脱冰对耐张串的冲击作用
当档距为800 m、第3档脱冰时,图2中TR耐张串的水平冲击效应最大,其最大水平冲击力为77.30 kN。当档距为800 m、高差为400 m、第3档脱冰时,TR耐张串的垂直冲击效应最大,其最大垂直冲击力为60.78 kN。
各档脱冰TR耐张串垂直冲击力随高差的变化如图10所示。
图10表明,不同档距条件下,高差越大,TR耐张串垂直冲击力就越大。
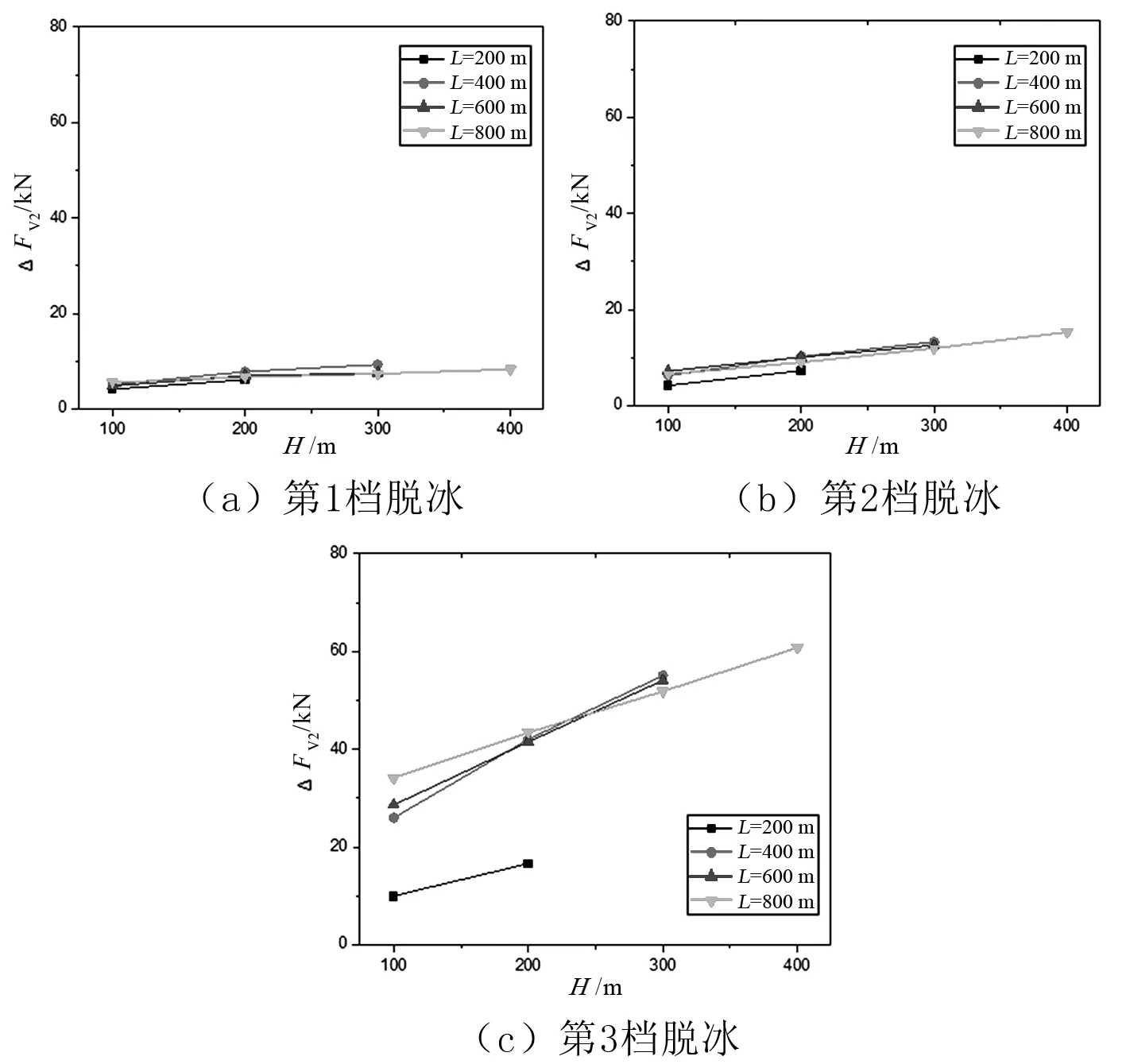
图10 各档脱冰TR耐张串垂直冲击力随高差的变化
5 结 语
上面基于脱冰计算理论,通过数值模拟方法研究了六分裂导线在档数、档距、高差等复合因素影响下导、地线的脱冰动力响应,分析不同参数条件下导线和地线脱冰对悬垂绝缘子串和耐张绝缘串的冲击效应和最不利控制因素。主要结论如下:
1)各种档距高差组合中,导、地线档距和高差均最大时,其冲击效应最大。
2)对于连续三档六分裂线路,悬垂绝缘子串挂点上的水平冲击作用在第3档脱冰时对V2串的冲击作用较第1档和第2档分别脱冰时的大;在第1档脱冰时,作用于V1串挂点的垂直冲击效应最大。
3)对于连续三档六分裂线路,导线脱冰过程中作用于耐张绝缘子串挂点上的冲击效应在最大号档脱冰时对右端(高位端)耐张绝缘子串挂点的冲击最大,水平冲击作用会随着档距的增大而增大,高差的影响较弱;垂直冲击作用会随着档距的增大而增大,也随高差的增大而增大。
4)地线脱冰过程中作用于耐张绝缘子串挂点上的冲击效应在最大号档脱冰时对右端(高位端)耐张绝缘子串挂点的冲击最大;脱冰时水平冲击作用会随着档距的增大而增大;垂直冲击作用会随着档距的增大而增大,也随高差的增大而增大。
