面向谐波治理的无源滤波器多目标优化模型
2021-07-21宁世红周思宇
宁世红,张 建,周思宇
(1.国网四川省电力公司德阳供电公司,四川 德阳 618000;2.电子科技大学机械与电气工程学院,四川 成都 611731)
0 引 言
随着现代电力系统中非线性特性负荷不断攀升,电力电子设备应用日趋广泛,谐波扰动问题日益突出。持续增加的谐波扰动,将导致系统用电设备产生额外热损失,缩短绝缘设备使用寿命,降低设备生产率和工作效率[1]。有源滤波器(active power filter, APF)和无源滤波器(passive power filter, PPF)是减少谐波扰动对系统影响,提升系统电能质量较为普遍的方法[2]。为了抑制谐波,滤波器一般建设在电网中具有大量非线性负荷和谐波扰动量较大的敏感位置[3];但是,由于谐波滤波器在进行谐波抑制的同时,会对系统功率因数、电压水平等其他指标造成影响,因此为了实现电网的全局最优,对谐波滤波器的容量及各项参数进行优化、确定最优配置方案就成为了必须要解决的关键技术问题。
文献[4]考虑了配电网中电压谐波畸变最坏情况,并以此作为依据确定了滤波器容量最优配置方案。文献[5]提出了单调谐滤波器分步配置方法,以配电网谐波治理效果为目标,求取滤波器最优容量配置方案。文献[6]利用Benders求解算法,将配置问题分解为以有源滤波器额定容量最小为目标的主问题,以及满足电网电压谐波含量为约束的子问题。文献[7]分别建立了微电网离散和连续解析模型,从而推导出有源滤波器的安装位置及容量。但以上研究均以谐波滤波器配置为单目标优化问题,使得优化结果存在不足。文献[1]建立了考虑无源滤波器建设成本、各次谐波有功功率网损、无功补偿容量的多目标优化模型,并通过细菌觅食智能算法对问题进行求解,证明了所提优化算法在满足多项指标约束条件下,比传统智能算法具有更快的收敛速度。文献[2]建立分别以无源滤波器建设数量最少为目标、谐波含量越限节点数量最小为目标的多目标优化模型,并联合ATPDraw(alternative transient program)电力系统暂态仿真软件和Matlab,对多目标问题进行求解,确定最优位置及参数配置方案。文献[8]采用模态分析法确定配电网中各次谐波滤波器的安装位置,同时考虑了投资费用、网络损耗及电压总谐波畸变率等多个指标,并通过分配各项指标的加权因子构建多目标问题的统一新目标函数,利用遗传算法对问题进行求解。文献[9]建立了以滤波器投资成本、无功补偿容量及谐波抑制效果为目标的无源滤波器设计多目标优化模型,并基于改进的粒子群算法在Matlab/Simulink工作环境下对问题进行求解,得到了最优参数设计方案。
现有研究通过配置有源和无源滤波器对谐波治理问题开展了研究,得到了相应的谐波滤波器参数设置方案。但相较于有源滤波器而言,无源滤波器不仅可以实现谐波抑制,又可以进行无功补偿,同时具有成本较低的优点,能够在实现谐波治理的基础上,降低投入成本。因此,下面提出了一种面向谐波治理的无源滤波器多目标优化模型。
1 无源滤波器工作原理
在治理谐波过程中,主要通过安装无源滤波器和有源滤波器,而无源滤波器具有结构简单、技术成熟、运行可靠性高等特点,得到了广泛的应用[10]
无源滤波器主要分为两种,即调谐滤波器及高通滤波器,而调谐滤波器又分为单调谐滤波器和双调谐滤波器[9]。由于双调谐滤波器主要是应用于高压直流输电系统中,在此仅考虑了单调谐滤波器。单调谐滤波器是通过电感与电抗的组合,在特定的频率上产生谐振,从而为电力系统提供谐波抑制以及减轻谐波扰动水平[3]。当谐波电流注入电网中时,滤波器支路会对特定频率下的电流呈现低阻抗特性,从而吸收在该频率下的谐波电流,最终达到降低电网总谐波含量的作用。无源滤波器基本工作原理如图1所示。

图1 单调谐无源滤波器工作原理
单调谐滤波器的谐振频率如式(1)所示。
(1)
式中:fi为单调谐滤波器第i次谐振频率;Li与Ci分别为第i次单调谐滤波器的感抗与容抗。
由式(1)可推导出滤波器发生谐振的条件,如式(2)所示。
(2)
式中:ωi为第i次谐波谐振角频率。
第i次单调谐滤波器的阻抗如式(3)所示。
(3)
式中:Zi为单调谐滤波器阻抗;Ri为单调谐滤波器电阻。结合式(1)—式(3)可以计算出滤波器品质因子,用于描述与谐振器调谐相关的带宽频率[3],如式(4)所示。
(4)
式中,qi为无源滤波器品质因子。
通过基波电压、基波电流与无源滤波器容量,可计算得到电容Ci,如式(5)所示。
(5)
式中:Qi为无源滤波器无功功率;ω1、V1分别为系统的基波角频率和基波电压。
2 多目标优化模型
2.1 目标函数
有研究将网络损耗[1,8]考虑为目标函数进行滤波器参数配置,但将外网等效为电压源的单谐波源问题时,网络损耗问题不是重点;也有文献将滤波器数量最小[2]设为目标函数,但真正决定滤波器投资成本的并不是数量,而是其配置容量,单纯将滤波器数量考虑为目标函数,并不能有效反应治理谐波所投资的成本。因此,所提优化算法同时以最小化滤波器投资费用及最小化系统总谐波畸变率建立多目标优化模型,实现投资费用与谐波治理效果的平衡。
1)最小化投资费用
为了确保谐波治理过程中,滤波器建设投资的经济效益,首先应该保证无源滤波器安装的成本尽量小,因此,投资成本目标函数如式(6)至式(7)所示,式(6)表示最小化无源滤波器投资总费用;式(7)为单调谐滤波器与高通滤波器建设费用计算方法。
minTE=TS
(6)
(7)
式中:TE为投资总费用;TS为单调谐滤波器建设费用;kr、kc、kl分别为电阻、电容与电感的单位投资成本,分别为8.8元/Ω、32元/mH、480元/μF。
2)最小化系统总谐波畸变率
(8)
式中:DTH为系统总谐波畸变率;Vi为各次谐波电压有效值。
2.2 约束条件
配置滤波器后,系统各项指标必须满足电能质量相关约束条件。式(9)表示谐波治理后,系统电压谐波总畸变率必须低于某一限值。
DTH≤DTH,max
(9)
式中,DTH,max为谐波畸变率最大容忍值。
式(10)表示单次谐波必须低于某一限值。
(10)
式中:DV,i为第i次谐波的含量;DV,max为单次谐波的含量限值。
为保证无源滤波器能够为系统提供足够的无功功率支撑,不出现欠补偿现象,同时,又须确保不出现过补偿,因此,必须保证功率因数维持在一定范围内,如式(12)所示。
Fmin≤F≤Fmax
(12)
式中:F为治理后系统功率因数;Fmin和Fmax分别为功率因数下限和上限,分别取0.94与0.99。
系统功率因数的计算参如式(13)所示。
(13)
式中:PL为负荷侧有功功率;QL为负荷侧的总无功功率。
同时,无源滤波器的投切数量,应该有一定限制,如式(14)所示。
Ns≤Ntotal
(14)
式中:Ns为无源滤波器投切数量;Ntotal为无源滤波器装设数量的上限。
品质因子也需要满足约束条件[3],如式(15)所示。
qmin≤qi≤qmax
(15)
式中,qmin、qmax分别为品质因子下限与上限,分别取30和60[3]。
2.3 多目标优化求解
两个目标函数会相互冲突,当不断改进任意的目标函数,必然会削弱另一目标函数的解。通过不断改进一个目标函数,并计算得到另一个目标函数值。所形成的解集在空间上形成的曲线可以清楚反映两个冲突问题之间相互妥协的耦合关系,这条曲线即为帕累托前沿。现有的大量研究主要采用求取帕累托前沿的方法,对多个目标的复杂问题进行求解,取得不同情况下的最优解集,并通过评价各解的优劣获得多目标问题的最优解[11-13]。所提方法也通过求解该多目标问题的帕累托前沿,得到两个目标之间的耦合关系,从而给出在实际工程应用中,不同应用场景下的无源滤波器最优配置方案。文献[14]在电能质量监测设备优化配置时,应用帕累托前沿求解了多目标问题,下面参考该文所述计算步骤进行求解:
1)仅以无源滤波器总配置成本为目标,以电压谐波总畸变率DTH=DTH,max为约束条件,对优化模型进行求解,得到相应的解TE,fun,该解即为所允许的建设成本最小值,即TE,fun=TE,min;

3)重复步骤2的计算,并设置约束条件无源滤波器总投资成本TE从最小值TE,min以步长δ不断增大,直至达到TE,max;
4)通过步骤1至步骤3的优化计算,得到电压总畸变率DTH在不同总建设成本约束下的优化结果,并生成帕累托最优前沿曲线。
3 算例分析
3.1 参数设置
以一个工厂作为算例,该工厂戴维南等效电路如图2所示。电网等效电阻Rs=0.007 8 Ω,电感Ls=81.49 μH,电压等级为400 V,基波频率为50 Hz。系统各次谐波电流含有量如表1所示,PCC处总畸变率为23.184%,谐波治理前功率因数为0.85。DV,max=3%,DTH,max=5%[13],无源滤波器最大投切数量Ntotal=4,所提优化算法在配置为Intel i5处理器、内存16 GB的计算机上实现。

表1 各次谐波电流含有量

图2 系统等效电路
3.2 结果分析
经过计算得到,在加入无源滤波器进行谐波治理前,公共节点(point of common coupling,PCC)各次电压谐波含有率如图3所示。由图可知,公共节点处的5次、7次、11次及13次谐波电压,均明显超过单次谐波含有量的上限。因此,须对这几次谐波无源滤波器进行参数配置进行滤波,消除谐波对系统的影响。

图3 谐波治理前公共节点处各次电压谐波含量
图4展示了多目标优化问题的最优解集,随着无源滤波器建设成本的增加,系统公共节点处的电压总谐波畸变率逐渐减小: 当建设成本最小时,有最大的电压总谐波畸变率;当投资成本达到最大时,系统谐波畸变率达到最小值。由此可知,无源滤波器总投资成本与总谐波畸变率是一个相互冲突的目标,当一个目标达到最优,必然导致另外一个目标值减小。因此,通过帕累托前沿曲线,可以根据工程实践需要选择具体建设方案。当建设预算充足,且公共节点电压畸变率尽可能低时,可选择图中B点优化方案;相反,当建设投入资金有限,且对电压畸变率要求不高时,可选择图中A点所示方案。但是,这两种方案相对较为极端,选择任何一种方案都将导致另一目标损失较大,因此,引入TOPSIS评估模型,对帕累托解集中的解进行综合评估,得到综合评价最优的解,为工程实践提供建设依据。TOPSIS评估方法,又称逼近理想解排序法。该方法能充分利用原始数据的信息,通过评价对象与最优方案和最劣方案间的距离,获得各评价对象与最优方案的相对接近程度,并通过接近程度对各解进行综合评分,得分的高低决定了解与理想解的接近程度。其结果能精确地反映各评价方案之间的差距,确定各方案评分步骤如式(14)至式(22)所示,其中:式(14)至式(15)表明对两个指标值进行归一化处理;式(16)至式(17)与式(18)至式(19)分别表示两个目标的最优值与最劣值;式(20)至式(21)表明帕累托解集中各解与最优方案和最劣方案之间的接近程度;式(22)表示值越大,评价对象越优越。经过TOPSIS综合评价模型评估,帕累托解集中的各方案的综合评分如表2所示。

表2 TOPSIS模型评估结果
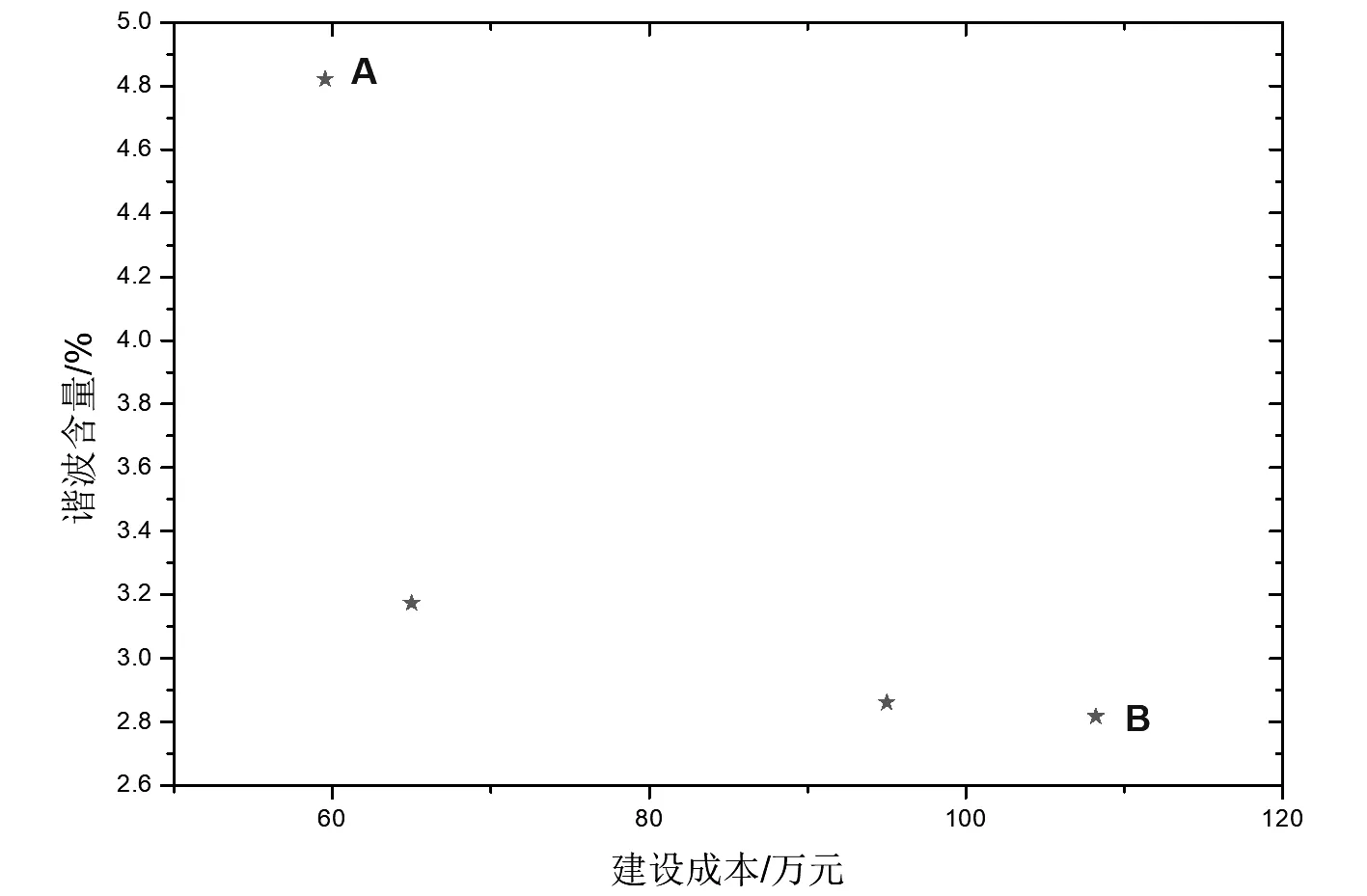
图4 多目标优化帕累托前沿
(14)
(15)
(16)
(17)
(18)
(19)
(20)
(21)
(22)

由表2可知,帕累托解集中最佳为方案2,在该建设方案下,建设总成本为65.01万元,电压总谐波畸变率为3.173%,功率因数F=0.95,各次谐波无源滤波器的具体建设方案如表3所示。

表3 无源滤波器配置参数
表3展示了在最优方案下的无源滤波器的配置方案,经过滤波后,公共节点电压各次谐波明显降低,如图5所示。由图5可知,经过无源滤波器滤波后,各次谐波含量全部低于限值,最大单次谐波含有量从15.729%下降到了治理后的0.902%。公共节点电压总谐波畸变率从23.184%下降到了治理后的3.173%,功率因数提升了11.765%,证明所提方法能够在控制成本的前提下,有效实现谐波治理。

图5 优化后公共节点处各次谐波含有量
4 结 语
为应对谐波扰动对电网的影响,建立了面向谐波治理的无源滤波器多目标优化模型,并通过一个实际的工厂作为算例,求解了多目标问题的帕累托前沿,并通过TOPSIS综合评价模型,得到了无源滤波器最优配置方案,验证了所提方法的科学性及可行性,得到如下结论:
1)同时考虑多个因素对谐波治理的影响,建立了无源滤波器优化配置的多目标优化模型,实现了在尽可能减少投入成本的情况下降低电网谐波污染的影响,保证了用户的用能质量;
2)引入了TOPSIS综合评估模型,对帕累托解集进行了评价,从而确定了无源滤波器最优配置方案;
3)所提方法将总谐波畸变率由治理前的23.184%降低至治理后的3.173%,功率因数由0.85提升至0.95,证明了所提多目标优化模型具有实际工程应用价值。
