含柔性负荷的火电机组深度调峰的源荷分层优化调度
2021-07-21樊国旗刘海南樊国伟段青熙潘伟东宋朋飞柳庆丰
樊国旗,刘海南,黄 健,樊国伟,段青熙,潘伟东,宋朋飞,柳庆丰
(1.国网金华供电公司,浙江 金华 321017;2.国网石嘴山供电公司,宁夏 石嘴山 753000;3. 国网新疆电力有限公司,新疆 乌鲁木齐 830011;
0 引 言
风电在促进可持续发展战略发挥着重要作用[1-2],但风电反调峰特性对电力系统调峰带来巨大挑战,需要优化系统运行促进风电消纳[3-4]。
针对此类问题,文献[5]通过预留部分负荷资源,在需要消纳新能源时,调用该预留负荷提高风电利用率;文献[6-7]通过调用高载能负荷实现削峰填谷作用;文献[8-9]通过火电深度调峰等多种途径促进新能源消纳;文献[10]在新能源出力高峰时段,通过抽水蓄能增大系统负荷,减少火电机组深度调峰功率;在新能源出力低谷时段,则由抽水蓄能电站放水发电减小火电机组发电压力。
上述文献多是针对源侧或负荷侧进行研究,较少综合考虑负荷和电源分层优化调度进行研究。因此,提出了一种含柔性负荷的火电机组深度调峰的源荷分层优化调度方法,通过上层优化减小系统峰谷差,减少系统开机台数,降低常规调峰最小技术出力;通过下层优化减小系统成本,确定火电机组出力和弃风功率。通过某地区电力系统实际算例,验证所提分层调度方法可有效促进风电消纳,降低系统成本。
1 风电并网对电网特性影响
风电具有逆调峰特点,并网后会加大电网等效负荷峰谷差。当等效负荷小于火电机组最小技术出力时,会导致弃风。等效负荷峰谷差计算如式(1)、式(2)所示。
Pe1,原始,t=P1,原始,t-Pwind,t
(1)
(2)
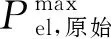
图1为某日风电、原始负荷、原始等效负荷和未深度调峰时弃风情况。可知,含风电等效负荷峰谷差为3 611.1 MW,不含风电等效负荷峰谷差2713 MW,增加了系统调峰负担893.1 MW;最大弃风功率1128 MW,充风量为5 066.7 MWh,弃风率为24.8%,弃风较为严重。因此需要考虑调用其他资源减小系统调峰压力,减少弃风。

图1 风电并网对系统的影响
2 柔性负荷、火电机组深度调峰分析
2.1 火电机组深度调峰
火电机组常规调峰由于受到最小技术出力(50%PN,PN为机组最大技术出力)限制,其调峰空间小。系统因调峰能力不足导致弃风,因此需要增加系统调峰能力。通过技术改造,火电机组最小出力可先降低至不投油火电机组最小技术出力(40%PN),然后再降低至投油火电机组最小技术出力(30%PN),这样可以增大火电机组调峰空间,进而接纳更多风电。火电机组出力变化如图2所示。

图2 火电机组出力变化
火电机组深度调峰主要产生机组损耗成本、投油成本。其深度调峰增加的成本为10~50元/MWh[11],而深度调峰补偿价格约为200元/MWh[12],由于增加火电机组收益,因此火电机组愿意参与深度调峰。
火电机组深度调峰机组损耗成本为
(3)
式中:β为机组损耗系数;SJ为机组购机成本;NF,t为机组t时刻的转子致裂周次,和火电机组出力大小有关。
火电机组深度调峰机组投油成本为
(4)
式中:Qoil,t为深度调峰投油量;coil为投油成本单价。
2.2 柔性负荷
柔性负荷可以改变生产时间,从而优化电网等效负荷,改善峰谷差特性。当需要柔性负荷(如电解铝)调峰时,首先采用电压调节功率,利用电解铝额定工作电压在±10%范围内变化不会影响产品质量特性进行调节;当所需参与调峰功率增加(减少)超过30 MW时,采用投入(退出)一组电解铝负荷(30 MW)进行调节,使电压恢复至额定工作电压,以此类推,从而可以实现柔性负荷连续调峰效果。柔性负荷参与调用如图3所示。
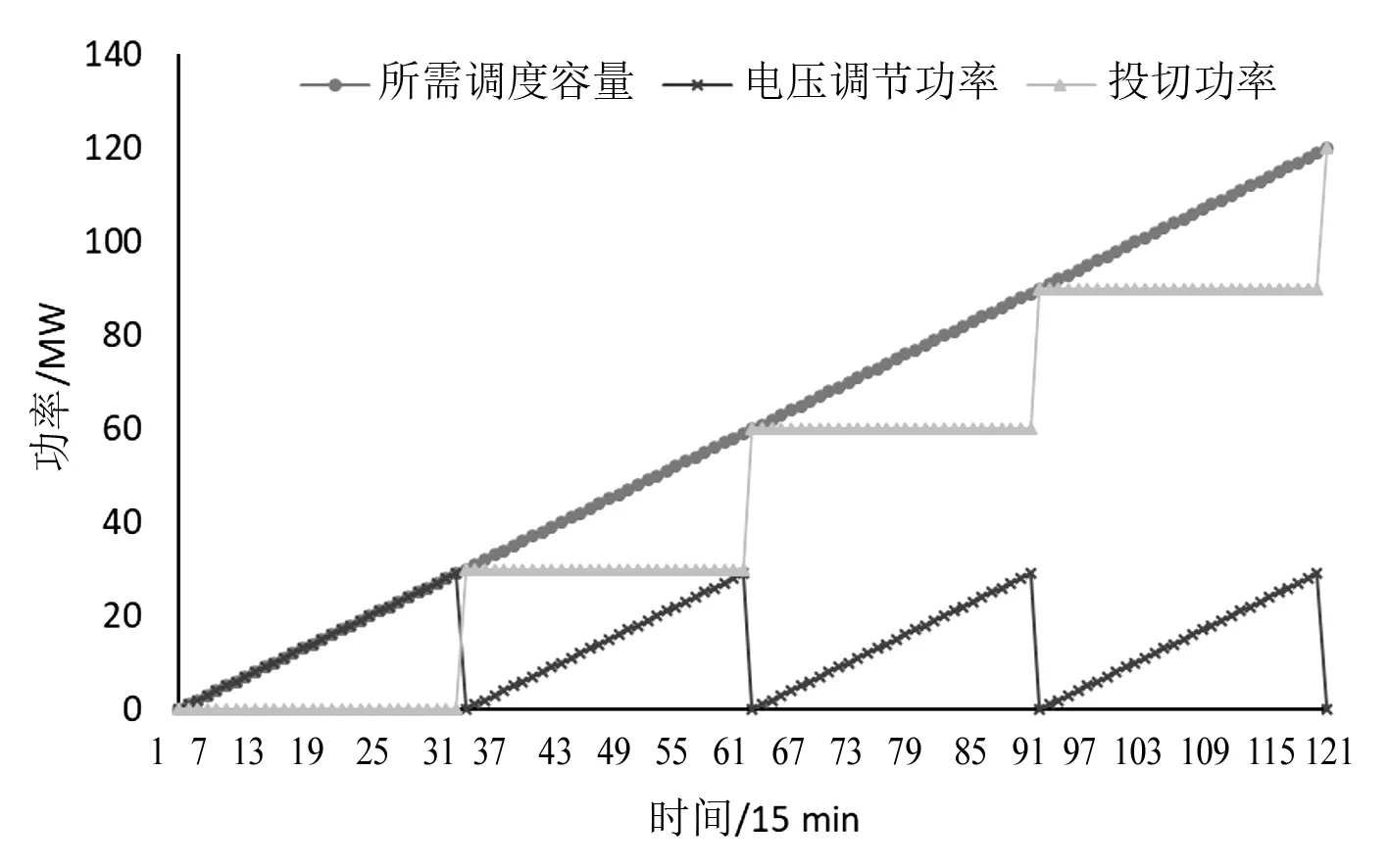
图3 柔性负荷参与调用
电解铝耗能大,因此对电价成本比较敏感,但转移负荷本身较为容易且不会增加成本,而获得的调用补偿可以减少生产费用。因此电解铝负荷参与调度意愿较强。
调用容量约束为
(5)
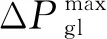
调用时间约束为
(6)
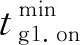
3 分层优化调度模型
3.1 分层优化调度模型结构
分层优化调度模型如图4所示。
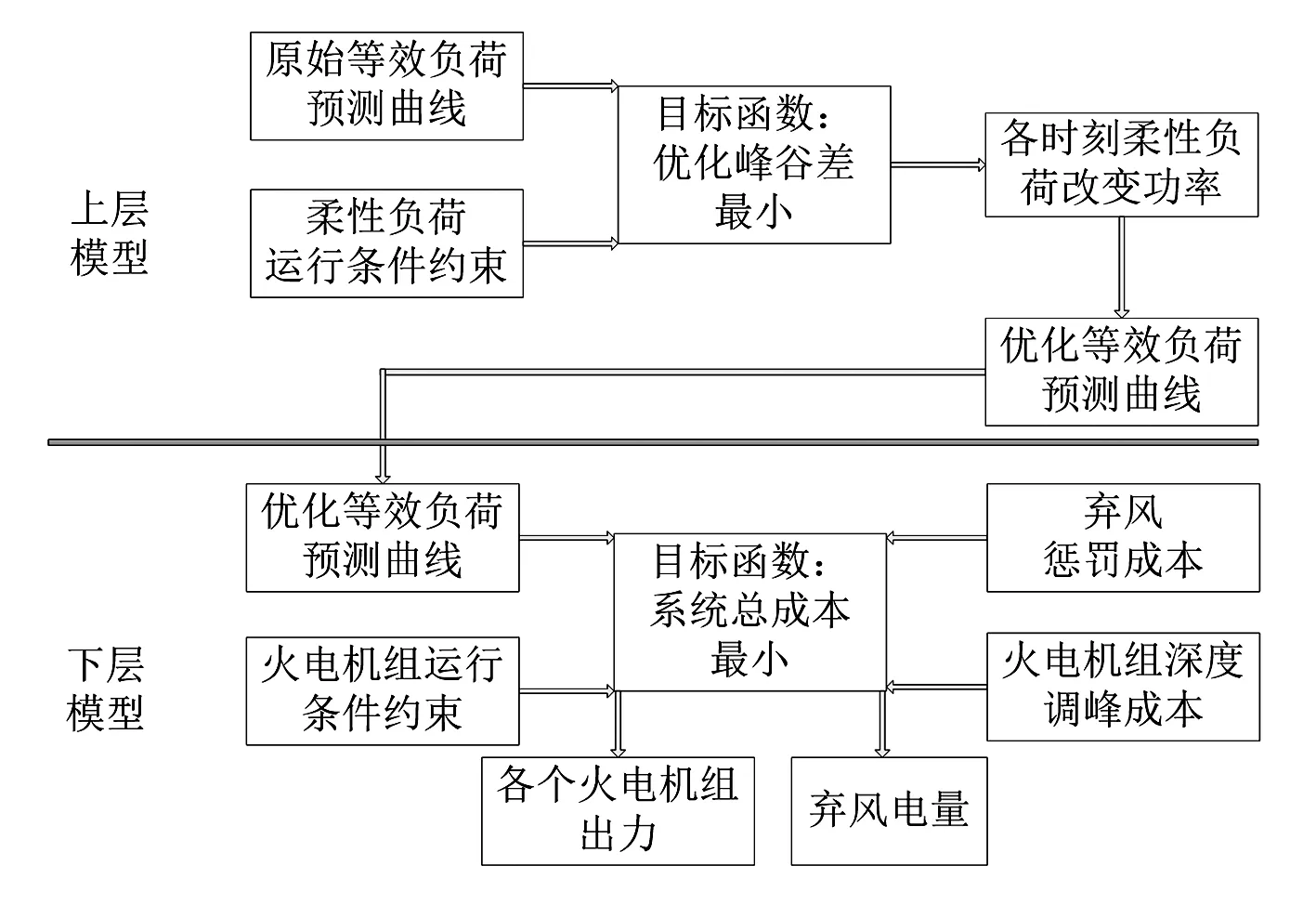
图4 分层优化模型结构
上层模型以优化等效负荷峰谷差最小为目标,提高火电机组低谷时间出力,减少深度调峰调用功率,进而减少深度调峰调用成本;降低火电机组高峰时间出力,增大火电机组向上调节能力(火电机组最大技术出力和当前出力差值),从而提高火电机组面对风电缺额或者其他火电机组故障时的风险能力。柔性负荷参与调峰后能够优化等效负荷曲线。
下层模型以系统成本最小为目标,系统成本包括火电机组成本、弃风成本和柔性负荷调用成本。火电机组容量越大成本越低,所以首先调用大容量机组深度调峰,其次调用小容量机组深度调峰。
3.2 分层优化调度模型目标函数
上层优化模型以优化等效负荷峰谷差最小为目标,即
(7)

总调用柔性负荷成本Cfl为
(8)
式中:ΔPfl,t为调用柔性负荷功率,ΔPfl,t为正表示增大柔性负荷功率, ΔPfl,t为负表示减小柔性负荷功率;T为调用柔性负荷时间;cfl为调用柔性负荷单位成本。
下层优化模型以系统成本最小为目标。
min(Cw,a+Cf)
(9)
式中:Cw,a为弃风成本;Cf为火电机组成本。
(10)
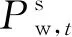
(11)
式中:T″为火电运行的时间总数;N为火电机组的数量;Pf,i,t代表第i台火电机组t时刻的功率大小;ai、bi、ci分别为第i台火电机组发电成本的二次、一次和常数系数;Cf,深度为火电机组深度调峰成本[10]。
3.3 约束条件
约束条件包括系统备用约束、系统功率平衡、火电机组常规调峰和深度调峰出力上下限约束,分别如式(12)至式(15)所示。
(12)
(13)
(14)
(15)
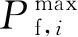
4 算例分析
4.1 仿真系统设计
以图1所示的风电并网数据和表1所示的火电机组参数进行仿真。火电机组最小技术出力为额定容量的50%。
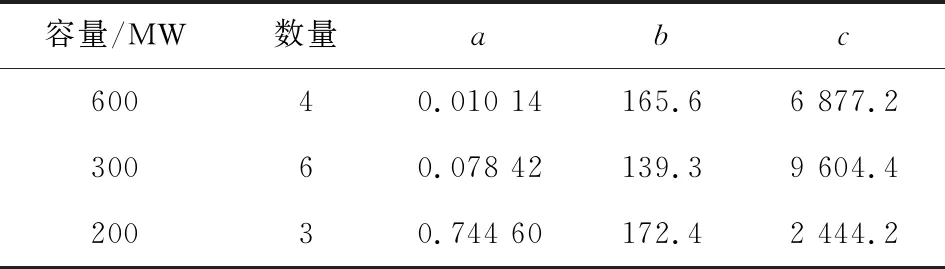
表1 火电机组参数
风电上网电价为250元/MWh,补贴电价为350元/MWh,弃风单位成本为600元/MWh;柔性调用单位成本为153元/MWh,柔性负荷参与调度每组容量为30 MW,最大可调用20组。
4.2 仿真验证结果
1)经仿真该日原始等效负荷、柔性负荷优化等效负荷、柔性负荷调用功率如图5所示。
由图5可知,在原始负荷低谷期增加调用柔性负荷为1 820.86 MWh,在原始负荷高峰期减小柔性负荷为1 148.3 MWh,总调用柔性负荷为2 969.17 MWh;柔性负荷优化后等效负荷峰谷差为2 571.8 MW,峰谷差降低28.78%;优化前最大等效负荷为4553 MW,优化后最大等效负荷为4113 MW,减小了440 MW;优化前最小等效负荷为1 541.8 MW,优化后最小等效负荷为941.9 MW,增大最小等效负荷599.9 MW。
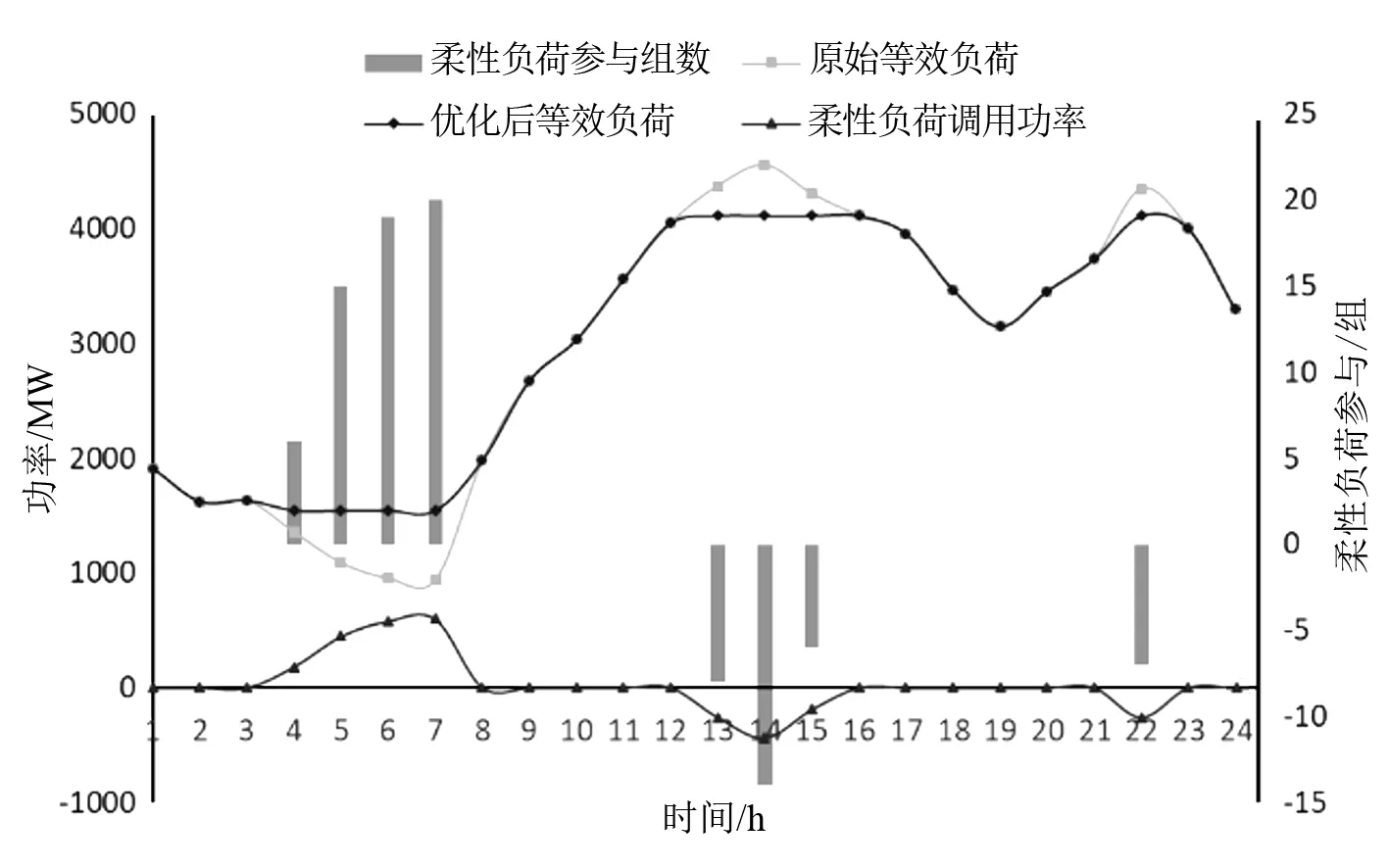
图5 柔性负荷优化等效负荷与原始等效负荷对比
2)柔性负荷优化等效负荷前后开机台数对比如表2所示。

表2 柔性负荷优化等效负荷前后开机数对比 单位:台
由表2可知,柔性负荷优化等效负荷后可减少200 MW机组开机两台。
3)柔性负荷优化前后等效负荷火电机组出力对比如图6所示。
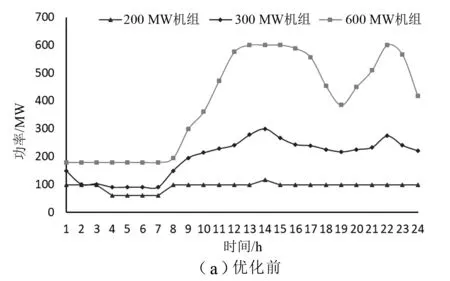
图6 柔性负荷优化前后火电机组出力对比
由图6可知:柔性负荷优化后提高火电机组平均出力,其中600 MW、300 MW和200 MW单台机组平均出力分别提高21.84 MW、15.51 MW和5.93 MW;提高了火电机组平均利用小时。
4)柔性负荷优化前后火电机组深度调峰和弃风功率对比如图7所示。

图7 柔性负荷优化前后火电机组深度调峰与弃风对比
由图7计算可知,柔性负荷优化前火电机组深度调峰为6 293.4 MWh,而优化后为4 285.9 MWh,减少火电机组深度调峰2 007.5 MWh;柔性负荷优化后没有弃风,而优化前弃风1 413.4 MWh,减少弃风1 413.4 MWh。
5)柔性负荷优化前后成本对比如表3所示。

表3 柔性负荷优化前后成本对比
可以看出,柔性负荷优化后火电机组运行成本减小了46.99万元,火电机组深度调峰成本降低了4.51万元,弃风成本降低了84.8万元,虽然柔性负荷调用成本增加了45万元,但总成本仍降低91.3万元。由于增加的柔性负荷成本45万元补偿给了柔性负荷企业,达到了柔性负荷企业和电网企业双赢的目的。
5 结 语
针对风电并网系统调峰能力不足问题,提出含柔性负荷的火电机组深度调峰的分层优化调度方法;上层优化等效负荷,可减小系统峰谷差;下层优化系统成本,减少火电机组深度调峰成本、新能源限电成本以及系统总成本。
通过仿真验证,所提柔性负荷优化火电机组深度调峰可以减少火电机组开机台数,提高单台火电机组平均利用小时。同时可以降低柔性负荷企业成本,达到电网企业和柔性负荷企业双赢的目的。
