特斯拉阀流场特性及空化形成机理数值分析

任 璞，龙 威

昆明理工大学 机电工程学院，昆明 650500

特斯拉阀因其特殊的结构和控制流动特性在微流体控制、微机电系统和生物化学等领域得到广泛应用[1-5].

近年来，国际上许多学者对特斯拉阀的结构和导通性能开展了大量研究[6-10].Thompson等[11]利用三维CFD技术，对多级特斯拉阀(multi-stage Tesla valve，MSTV)的有效性进行了量化，并研究了低雷诺数和不同阀阀距离下多级特斯拉阀的有效性.Porwal等[12]通过数值分析研究了进口雷诺数(25～200)对单个特期拉阀和MSTV(10级)整流和热增强能力的影响.Qian等[13]通过数值分析对Al2O3-水纳米流体微尺度T45-R型特斯拉阀的流动特性进行了研究.钱锦远等[14]采用数值模拟的方法，对不同参数和级数的特斯拉阀型微通道热沉的强化换热进行了研究.

但目前对于特斯拉阀的研究多倾向于结构和正向导通时的研究，对于特斯拉阀逆向导通时的空化现象[15]及其形成机理的研究还不多见.因此，本文从特斯拉阀逆向导通时流场特性入手，对特斯拉阀交叉出口处流场特性进行详细分区分析，研究逆向导通时特斯拉阀发生空化的原因，同时对比加入空化模型前后，空化效应对流场特性的影响.

1 模型的建立

1.1 几何模型

本文以图1(a)所示结构的特斯拉阀为研究对象，结构参数如图1(b)所示.通道截面形状参数为10 mm×10 mm的矩形.

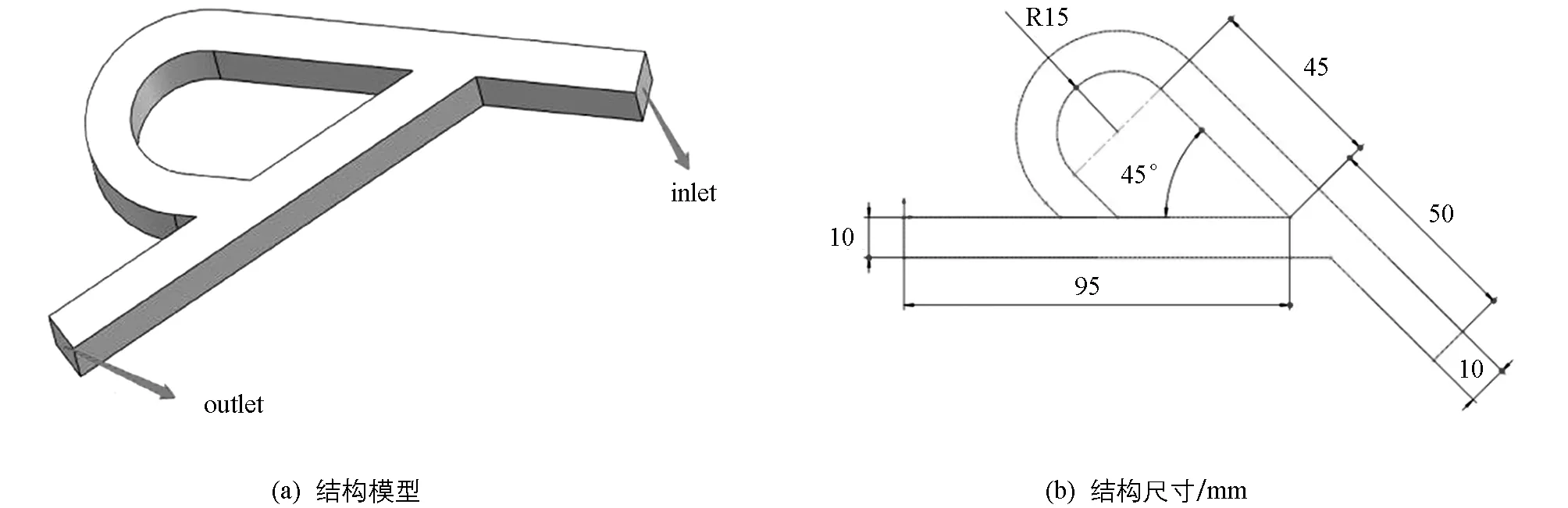
图1 特斯拉阀结构尺寸

1.2 数学模型

1.2.1 空化模型

当流体中局部压力低于流体的空气分压力时，流体中融入的气体会析出，发生空化现象.特斯拉阀反向导通时，阀体的交叉出口处会产生局部低压，当阀体进出口压差较大时，交叉出口处就发生空化.采用mixture模型中Zwart-Gerber-Belamri(ZGB)空化模型对流场进行表达计算，液相-汽相质量传递由蒸汽传输方程表示如式(1)所示：

(1)

式中v表示气相，α为蒸汽体积分数，ρv为蒸汽密度，vv为气相速度，Re，Rc分别为与蒸汽泡生长、破裂相关的传质源项.在ZGB模型中，气相和液相之间的总相间传质率R为

(2)

式中RB为气泡半径，取值10-6m；PB为气泡压力；P为流体当前压力；ρl为液相密度.建立空化模型如下式所示：

当P≤Pv，则

(3)

当P≥Pv，则

(4)

式中Fvap为蒸发系数，取值50；Fcond为冷凝系数，取值0.01.

1.2.2 网格划分及边界条件

以六面体网格为主对几何模型进行网格划分，网格尺寸限制为0.4 mm，模型总网格数为57万，如图2所示.边界条件设置如表1所示.

表1 边界条件

图2 网格划分

2 流场特性分析

利用Fluent平台，以图1所示的模型为研究对象，反向导通条件下对阀内流场进行分析.采用多相流欧拉空化(mixture)和标准k-ε湍流方程相结合的模型，设定流体密度为998.2 kg/m3，动力黏度为0.001 003 Pa·s，空化气相(vapor)密度为0.554 2 kg/m3，动力黏度为1.34×10-5Pa·s，空化模型选用Zwart-Gerber-Belamri模型，具有较高的计算精度以及较好的收敛性，空化压力为4 133 Pa，压力-速度耦合器选择Coupled算法，计算结果收敛残差小于10-6.

2.1 流场分析

首先对特斯拉阀反向导通时流场特性进行分析，明确流场内部的高速、低速和高压、低压区域的形成原因.

由图3(a)速度云图可知，特斯拉阀逆向导通时，直通道中共有1、2两处低速流体区域.

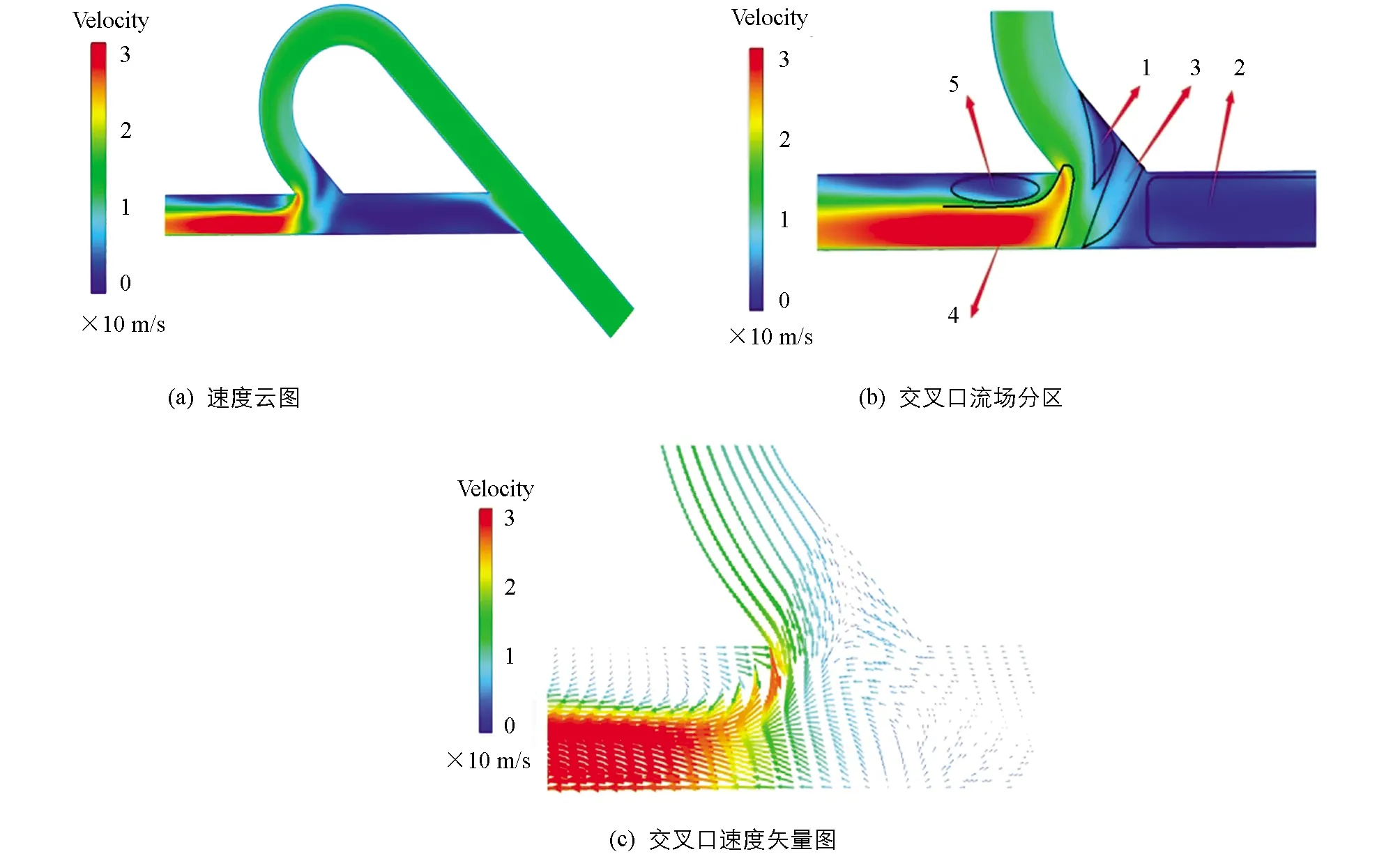
图3 流场速度

区域1(射流末端区域)的流体流速较低是由于弯管出口处的高速射流与交汇处直管中流出的流体发生冲击，产生的速度梯度较大，速度迅速降低，且由于两个方向流体的冲击作用，弯管出口处的高速流体产生沿垂直方向的转向.

区域2流体速度较低，一方面是由于分叉入口进入区域2的流体较少，流速较低，另一方面是由于弯管中的流体高速射流流出弯管后与直管中水平流动的流体发生冲击，阻碍了区域2中流体的流动，因此区域2中流体流速较低，压力较大.

区域3的流体流速较高是由于此区域流体冲击后发生转向，流速较高，且由于射流冲击和流体流向的转变，在区域3中形成如图4所示的2个涡流.

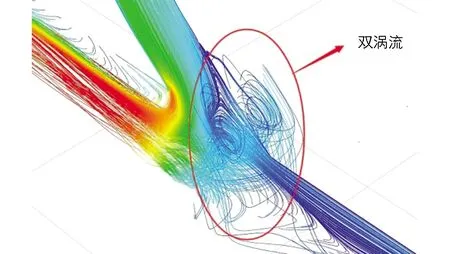
图4 涡流图

受区域1和区域3共同影响，弯管中的高速射流绝大部分在1、3区域左侧发生垂直转向流入左侧水平通道中，即图3(b)中的区域4.区域4的流体流速最大，一方面是弯管中的高速射流转向后流入，另一方面是区域4右侧均为高压区域，左侧联通出口为标准大气压，形成较大压差.

由图5压力云图可知，弯管-直管交叉处右侧压力较大，左侧压力较低，且区域4、5最低压力低于液态水的空气分离压4 133 Pa.其中区域4压力较低是由于流体流量和流速较大.

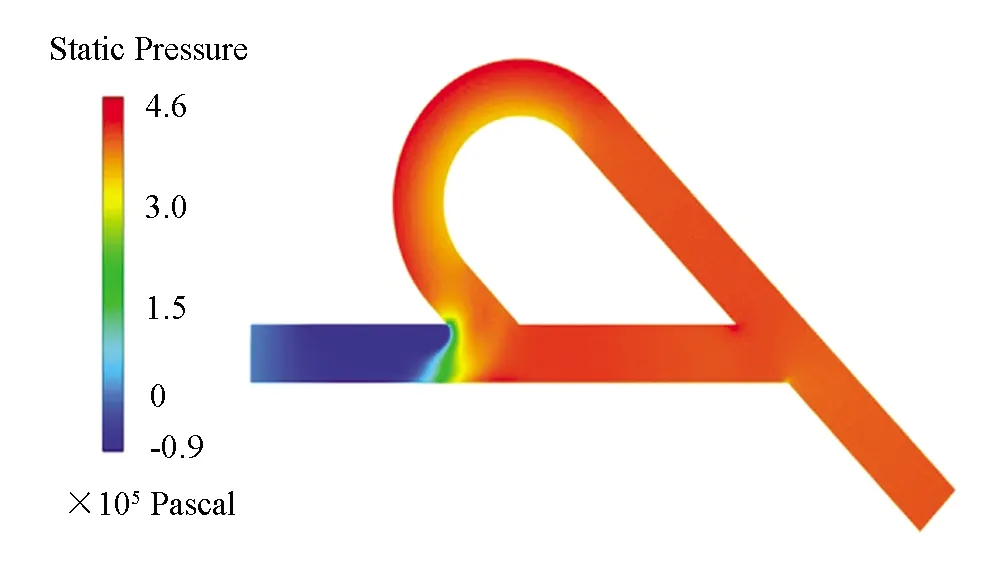
图5 压力云图(空化)

2.2 空化效应

由水力空化效应可知，当通道内流体压强降低至空气分离压时，流体内部气核析出形成气泡.由于区域5最低压力低于液态水的空气分离压，因此在计算模型中加入多相流的欧拉空化模型(mixture)对计算模型进行修正.数值分析发现：如果忽略空化效应，会在流场内部形成过低负压与实际情况不符.

图6所示为未考虑空化时的流场压力，由于计算模型中没有空化模型，压力会随流体流速增大不断下降，压力最低值为-3.66×105Pa.而图5中，考虑空化时，由于空化效应的存在，流体发生空化，压力最小值为-9.92×104Pa.因此，在对特斯拉阀逆向导通过程进行数值分析时，考虑空化效应的影响是必要的.

图6 压力云图(无空化)

由图7可知，空化效应集中发生在低压区域5.由上述分析可知，弯管-直管交叉处右侧压力较大，左侧压力较低，形成巨大压差；由图3(c)速度矢量图可知，直管中的少量流体和弯管中绝大部分的高速流体转向之后集中流向区域4.当入口压力为0.5Mp时，区域4的最高速度可达30.9 m/s，由于流体本身流量、流速很大，加之较大的压差，使汇聚后的流体高速流过区域4，因此会在区域5形成低压区域，当压力降低至流体空气分力压时，区域5流体发生空化，且由于特斯拉阀出口处压力为标准大气压，因此空化区域并未延伸至出口处.

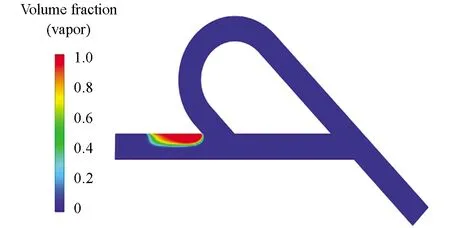
图7 空化效应

对比空化模型对交叉出口之后的流场特性的影响，图8所示分别为不考虑空化和考虑空化的后半段流场特性.

由图8(a)可知，无空化模型时，流场内部不会发生空化，区域5因区域4的高速转向流体所产生的牛顿内摩擦力形成涡流，涡流强度取决于转向流体的速度大小.加入空化模型后，由上述分析可知会将区域5流体中气体析出，产生不同程度的空化现象，因此区域5几乎不会产生大的涡流，而在区域5之后由于流体流速减小流体垂直扩散而产生较小的涡流，涡流更接近出口区域.

2.3 空化效应对流场湍流强度影响

由流场特性和空化效应分析可知，考虑空化效应时，交叉出口左侧区域流场会由于空化效应导致涡流更小更接近出口区域，对特斯拉阀出口处流体湍动能和空化区域温度将产生影响.

由图9湍动能的对比，结合图8中流场迹线涡流位置及大小可知，空化模型的加入对特斯拉阀弯管-直管交叉处左侧区域湍动能产生极大的影响，无空化模型中，交叉出口左侧为涡流产生区域，此处湍动能极大，峰值为8.4×104m2/s2；由于空化效应的存在，交叉出口左侧空化区域发生空化，涡流更小且更接近出口区域，因此湍动能极小且发生湍流的主要区域也更接近出口区域，湍动能峰值为5.6×10 m2/s2.

图8 流场迹线

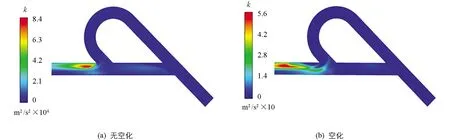
图9 有无空化的湍动能

3 结 论

1)基于Fluent仿真平台，采用多相流欧拉空化和标准k-ε湍流方程相结合的模型，从流体动力学角度出发，将特斯拉阀反向导通时交叉出口处的流场分为5个区域，通道内存在2个低速流体区域，1个双涡流区域，1个空化区域和1个高速流体区域.

2)对比有无空化模型的影响，无空化模型流场压力最低值为-3.66×105Pa，通道内部压力峰值为4.6×105Pa；加入空化模型后，压力最低值为-9.92×104Pa，压力峰值为4.6×105Pa，空化模型对压力峰值无明显影响，但会显著提升最低压力值；加入空化模型，交叉出口左侧的涡流更小且更接近出口区域；同时涡流的减小与左移，可以极大减小交叉出口左侧湍流动能强度，湍动能峰值为5.6×10 m2/s2.