多元线性回归在风景园林项目工程限额设计中的应用

邹玉萍

孙卫国*

中国传统的风景园林工程项目管理模式常会出现工程设计和造价控制脱节的现象[1]，较多开发商会轻视风景园林项目工程设计阶段的造价控制，而将造价控制的关键放在施工阶段[2]。从整个风景园林工程项目的生命周期来看，风景园林工程项目的设计阶段是对整体空间、功能、景观等综合结果的一个预期，决定着整个风景园林工程项目的原材料、功能、景观布局、施工方案、施工时间和最终效果等[3]。因此，设计阶段在整个风景园林工程项目的生命周期中发挥着承上启下、不可替代的作用。风景园林工程项目的设计阶段由于还没开始施工，即使是大范围调整和改动都比较容易，而在施工阶段再进行修改就十分复杂[4]。为了保障风景园林工程项目的最终景观效果达到预期，并且满足居住者所需的各种功能，同时把投资效益最大化，就需要在设计阶段主动进行限额设计以达到造价控制[5]。有学者指出，在设计阶段重新进行造价控制而实现投资效益最大化的可能性为90%，而在施工阶段重新对造价进行控制达到投资效益最大化的可能性仅为10%[6]。当前已有大量造价控制模型引入到工程项目建设的各个阶段以达到造价控制，包括建筑信息模型(BIM)、系统动力学模型、价值工程模型、项目管理成本控制模型、LUBA模型和三角模糊数模型、回归模型及开发决策支持系统模型等，这些模型经过实际的样例运行，均在建筑工程造价控制中表现出较好的适用性和准确性，但这些模型在风景园林工程限额设计中的实用性和准确性还缺乏相关的证据。

随着中国经济的快速发展，各个城市的房价在近年来持续走高，越来越多的居民无法负担舒适型及豪华型住宅；而经济型住宅及景观具有功能性、实用性和经济性的特点，并且经济型住宅在景观投资预算上有限。因此，在经济型住宅风景园林工程项目设计阶段引入限额设计以主动控制工程造价十分必要。由于线性回归模型具有操作简单、准确度可靠的特点，本文将基于因子分析建立多元线性回归模型对经济型住宅风景园林工程项目的历史数据进行分析，从而为经济型住宅风景园林工程项目的限额设计提供预测和指导。

1 风景园林工程项目限额设计模型的建立和分析

1.1 风景园林工程数据的收集

中国住宅风景园林建设目前正处于初期发展阶段，部分住宅的风景园林景观投入了较多的资金，但最后建造出来的景观从舒适度、美观度上来看都没有达到预期的效果。广东的经济总量和常住人口连续多年位居全国第一①，其优越的经济环境和地理位置也不断吸引着外来人才的流入，良好的园林景观可吸引购房者的注意力，并为住户提供愉悦的视觉体验和舒适生活。因此，以广东近年建造的住宅风景园林工程项目为研究对象，收集2017—2019年广东省多个区已实施的风景园林工程项目32例，数据涵盖工程建设各阶段的造价资料，包括可行性研究、投资结算、初步设计概算、施工图预算、合同价、结算及竣工决算等数据。

1.2 因子的确定

因子分析法是指利用少量的因子变量来代表工程的大部分信息[7]。对于广东风景园林工程而言，在市场、政策及人力这些不可抗因素一定的情况下，影响风景园林工程基本模块、子模块费用的主要因子为各子工程的人工成本、主材成本和机械、辅材成本。通过收集的数据发现，广东风景园林工程主要由园建工程、绿化工程和水电工程三大子工程组成，由于单方造价指标相比总造价成本指标能够更快速地初步判断风景园林设计的准确性、可行性和合理性，因此本研究初步设计了园建人工单方A1、园建主材单方A2、园建机械辅材单方A3、绿化人工单方B1、绿化主材单方B2、绿化机械辅材单方B3、水电人工单方C1、水电主材单方C2和水电机械辅材单方C39个因子，并以风景园林工程总造价y为因变量，将32个工程依次编号为1，2，3，……，32。通过对各工程的数据进行计算和处理，可得各个工程的风景园林工程总造价和各个因子的数据，如表1所示。

表1 因变量和因子数据表

1.3 因子分析结果

通过SPSS 26.0数据统计软件对上述9个因子进行因子分析，采用KMO和Bartlett检验，以比较各因子间的相关性和偏相关性。

可得KMO检验统计量为0.808，表明这9个因子的相关系数平方和远大于偏相关系数平方和，适合作因子分析。而Bartlett's球形检验的结果显示Sig.＜0.05(即P＜0.05)，表明9个因子间具有相关性，因子分析有效(表2)。

表2 因子分析检验结果

通过主成分分析结果来看，各因子的“提取”值均大于0.7，表明变量能被各因子表达得较好。从表3、4可以看出，前2个因子即可将变量表达至90.30%，前6个因子可将变量表达至99.35%，但由于各因子的提取值均大于0.7，为了追求更准确、可靠的模型，本研究先初步将9个因子均纳为多元线性回归模型的变量。

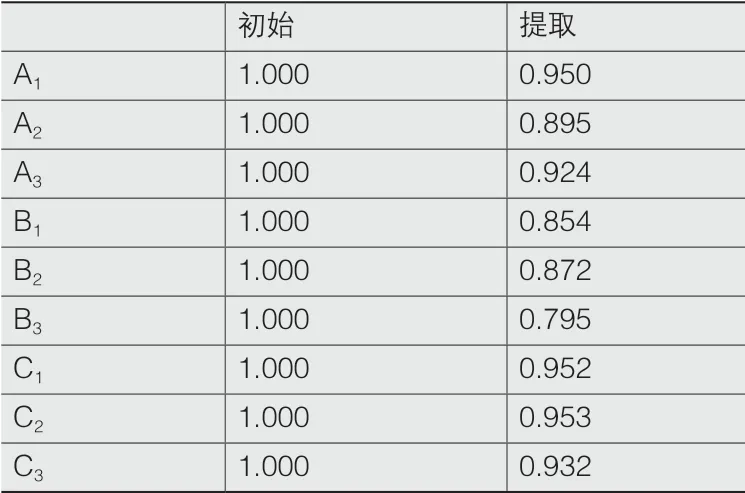
表3 主成分因子分析结果

表4 总方差解释表

同时，对不同总单方造价区间的各指标值进行95%置信区间计算，可得表5，以期为风景园林师在进行设计时提供指导和参考。

表5 风景园林工程不同造价区间对应的不同指标单方造价指导表

1.4 多元线性回归模型的建立

为了建立风景园林工程限额设计的多元线性回归模型，提取因子分析中表达较好的因子，设模型为：

式中，A1，A2，…，C3为因子；D为常数；a，b，…，i为因子系数。

通过SPSS 26.0软件进行回归分析以建立多元线性回归模型，统计检验包括模型的R方检验、模型的德宾-沃森(DW)检验、模型的F检验和因子的t检验、置信区间等，可得如下统计结果。

SPSS结果分析如表6所示，模型在调整前后的R方均大于0.99，说明模型的拟合效果极好，DW值为1.789，代表各变量间无自相关现象。而表7的数据显示模型的显著性Sig.小于0.05，说明在该优化模型中风景园林工程单方造价和这9个自变量之间存在显著的线性关系。

表6 模型摘要表

表7 ANOVA结果表

从表8可以看出，部分变量不具备显著性，需从模型中剔除部分变量以保证模型的可靠性和有效性。

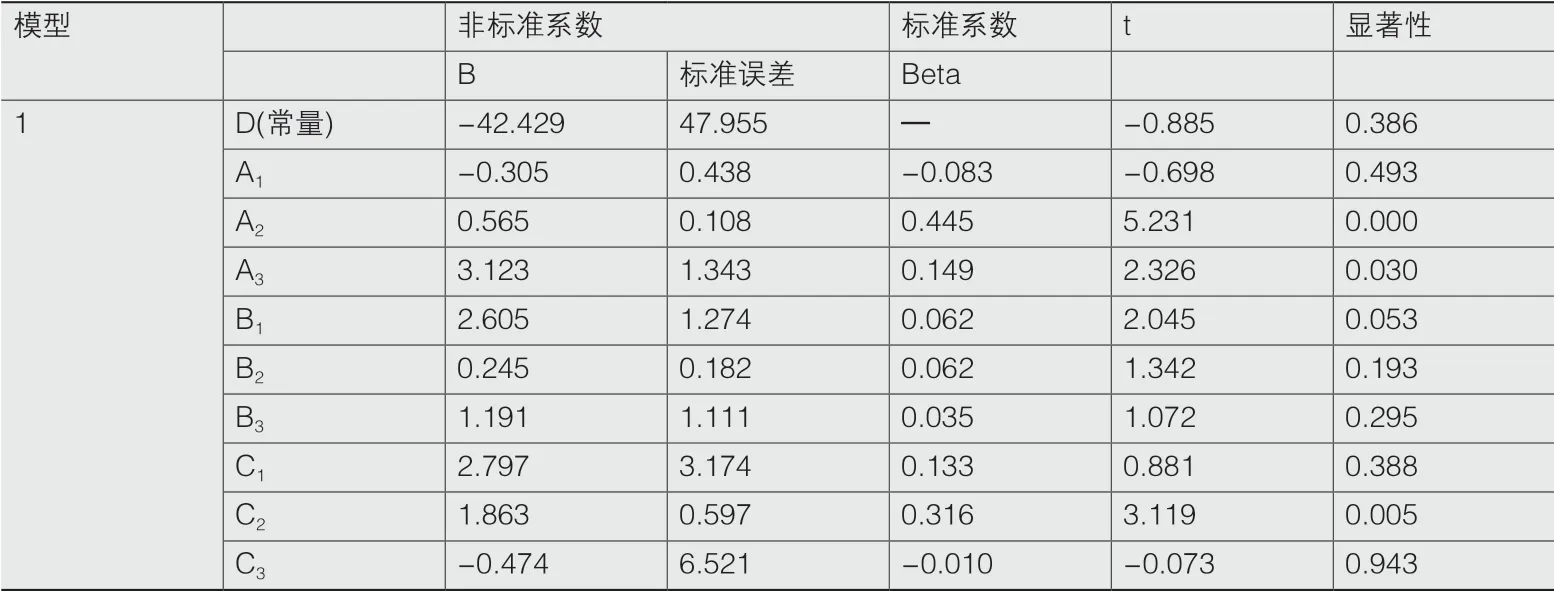
表8 系数结果表

1.5 多元线性回归模型的优化

通过剔除部分变量并进行回归分析，以验证优化后模型各变量的显著性，最后发现当对A1、B3和C33个变量进行剔除时，得到的回归模型各变量均具有可接受的显著性，因此设优化模型为：

Y＝aA2＋bA3＋cB1＋dB2＋eC1＋fC2＋g

对其进行回归分析后，可得如下统计结果。

从优化后的模型统计结果可知，模型在调整前后的R方均大于0.99，说明模型的拟合效果极好，DW值为1.736，代表各变量间无自相关现象(表9)。而表10的数据显示模型的显著性Sig.小于0.05，说明在该优化模型中风景园林工程单方造价和这6个自变量之间存在显著的线性关系。从表11中的数据看，A2、B1、B2和C2的P值小于0.05，具有较好的显著性；而A3、C1的P值小于0.1，在α=0.1时具有较好的显著性，因此该模型的显著性较好。

表9 模型摘要表

表10 ANOVA结果表

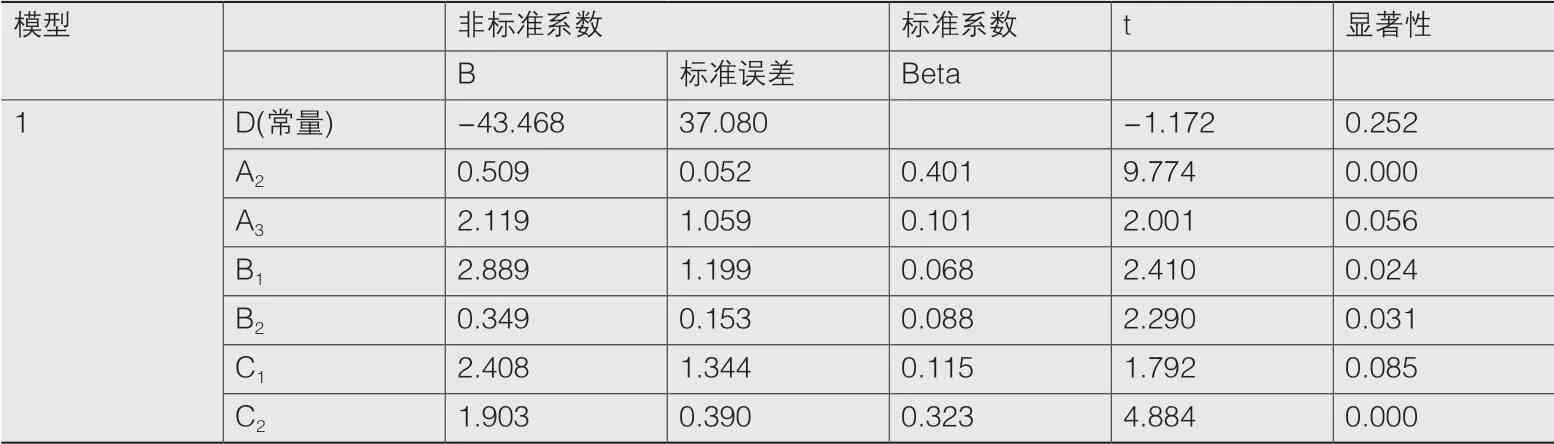
表11 系数结果表

因此，优化模型的方程为：

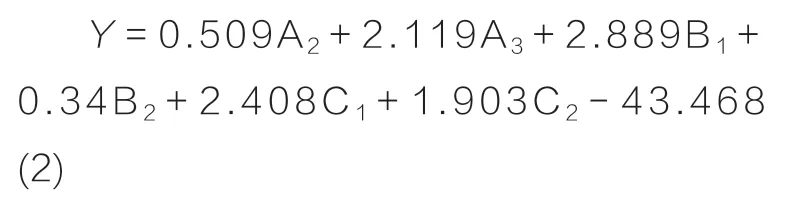
2 风景园林工程设计阶段的限额设计评价

为了验证限额模型的可靠性和在风景园林工程设计阶段的指导有效性，同时由于当前在风景园林工程限额设计评价体系方面的研究还较为空缺，因此，本文采用层次分析法[8](Analytic Hierarchy Process，AHP)对经济型住宅风景园林工程的限额设计进行评价，将评价体系分为3个层次：总目标层、目标层和方案层。其中，总目标层包含3个元素，为广东经济型住宅风景园林工程限额设计的有效合理性评价；目标层包含3个元素；方案层包含9个指标。通过当前建造的32个风景园林工程的各单方造价平均值，确定了各指标的权重，如表12所示。

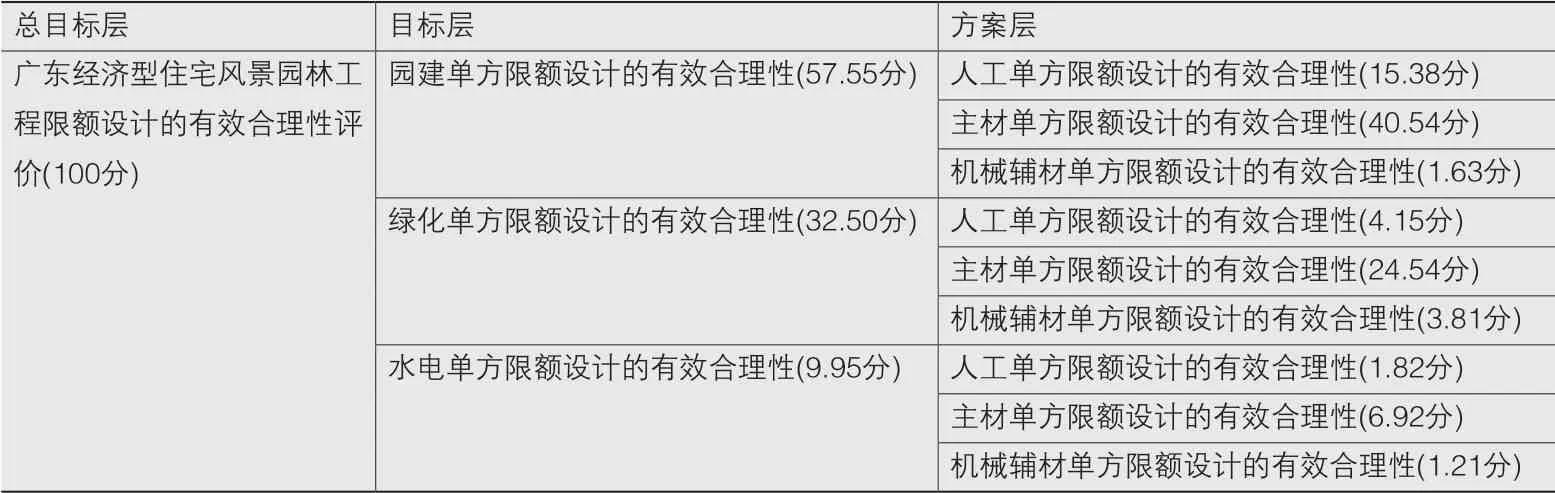
表12 风景园林工程评价模型

采用指标标准化方法对风景园林工程的单方限额指标进行标准化处理，再对其进行评价。指标标准化处理是为了消除量纲，将各指标转化成无量纲、无数量级差别的标准分，然后再进行分析评价。

指标标准化公式为：

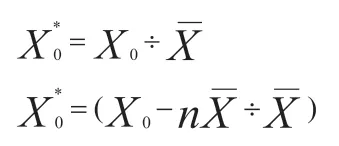
式中，X0＊表示经过标准化处理的指标值；X0表示工程的原指标值；表示指标的平均值。公式(3)用于X0＜时，公式(4)用于X0＞时，n＝1，2，3，4……

可得评分公式为：

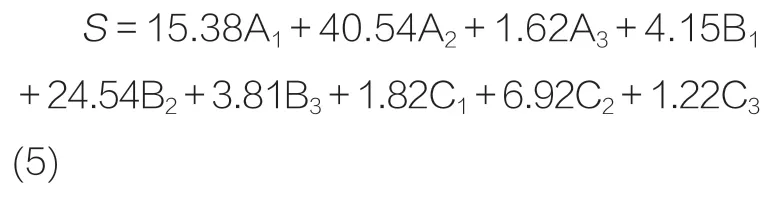
通过对广东32个风景园林工程数据进行评分可知，当前广东经济型住宅风景园林工程的平均评分为64.40分，最高的13号工程评分为86.42分，最低的为23号工程35.53分，大多数风景园林工程的评分在50～80分，说明限额设计较为合理。

3 限额设计模型的实例应用验证

3.1 某案例的风景园林工程方案

为了验证本文基于因子分析建立的多元线性回归模型在经济型住宅风景园林工程限额设计中的可靠性和有效性，选取广东某还未开发的项目作为案例，对其进行验证，该项目长边153m，短边70m，由2栋塔楼和1栋商业楼组成，2栋塔楼相对形成中庭，塔楼间距为43m。

其风景园林工程设计的原方案造价如表13所示。通过原方案的造价数据可得园建、绿化和水电的各指标单方造价(表14)，并对各指标进行标准化处理以进行评分。

表13 风景园林工程方案造价数据

表14 风景园林工程原方案单方造价及指标标准化处理

通过公式(2)可得该风景园林工程的总单方造价为752.82元/m2，则其预测总造价为639.90万元，其与原方案的计划总单方造价值731.75元/m2的误差为2.88%，符合国家规定的限额预测允许误差要求，即误差范围在-10%～+10%。通过公式(5)可得原方案的评分为52.08分，说明其限额设计还有较大改进空间。

3.2 方案的改造和优化

由于开发商的预算不足，无法承担621.73万元的开发成本，要求保持风景园林工程的总面积8 500m2，将风景园林工程的总单方造价由之前的731.75元/m2下调为400元/m2，总造价下调为340万元。因此，通过表5中各变量建议值对该案例的各变量进行调整，然后通过限额设计模型(2)对工程的总造价进行预测，以对方案进行改造和优化，改造后的风景园林设计方案如表15所示。

表15 风景园林工程改造方案

通过改造方案的数据，可得园建、绿化和水电的各指标单方造价如表16所示，并对各指标进行标准化处理以进行评分。

表16 改造方案的单方造价及指标标准化值

改造后的风景园林工程方案实际造价为296.74万元，总单方造价为349.11元/m2。而通过公式(2)对该工程的总造价进行计算，可得该风景园林工程的总单方造价预测值为333.06元/m2，则其预测总造价为283.10万元，其与改造方案的预测总单方造价366.06元/m2的误差为-9.01%，符合国家规定的限额预测允许误差要求。同时，通过评分模型公式(5)，可得改造方案的新评分为91.50分，相比原方案的52.08分有显著性提升(P＜0.05)。尽管开发商的投资预算大幅削减，但通过本文的限额指标和限额设计模型指导，将较多的主材都换成了成本更低但功能与原方案相同或相似的材料，使得优化后的方案与原设计方案的风景园林工程在功能性上相同或接近，但更具经济性，可有效防止开发商因资金链断裂而导致风景园林工程项目烂尾。

4 结论

限额设计、经济技术指标分析及价值工程等工具是目前应用最为广泛且造价控制效果最理想的设计阶段的造价控制方法。但由于风景园林师的造价控制和专业素养还有一定的不足，使得风景园林师在设计阶段无法掌握造价控制的主动权，只能跟随工程进展以事后预算或概算的方式进行造价控制。而限额设计是在设计阶段主动进行成本控制的一种方法，是指以成本作为重要的设计参数进行约束与指导的一项重要措施，有助于提高设计阶段的事前成本控制效果。预测和控制工程造价的模型方法已成为当前工程造价管理的重要组成部分，而单方造价指标的控制又是实现工程造价管理的精髓所在。当前已有较多的学者将多元线性回归模型运用到住宅工程、水电工程和建筑工程等工程的造价控制上，通过对以往实际工程数据建立多元线性回归模型，并通过多元线性回归模型对之后的工程单方造价进行预测和指导，其结果均显示多元线性回归模型的预测值和实际值非常接近，可有效、准确地实现工程的造价控制。而本研究基于因子分析法建立了广东风景园林工程的限额设计模型，模型共涵盖6个因子，分别为：园建主材单方A2、园建机械辅材单方A3、绿化人工单方B1、绿化主材单方B2、水电人工单方C1、水电主材单方C2。最终模型结果为Y＝0.509A2＋2.119A3＋2.889B1＋0.349B2＋2.408C1＋1.903C2－43.468，同时，本研究基于层次分析法建立了广东风景园林工程限额设计评价模型，评价模型公式为S＝15.38A1＋40.54A2＋1.62A3＋4.15B1＋24.54B2＋3.81B3＋1.82C1＋6.92C2＋1.22C3，通过实证也证实了本研究基于因子分析法建立的多元线性回归模型在指导风景园林工程的限额设计和造价预测上具有较好的可靠性和准确性。

注释：