基于Bootstrap和Bagging时间序列模型的黑龙江老龄人口预测

张敬信 秦蔚瑶 罗志坤

【摘  要】黑龙江省自2005年进入人口老龄化阶段并且人口老龄化趋势越来越严重，由此产生的影响需要全社会为此做出相应的措施。本文搜集黑龙江省1982年～2019年的65岁及以上老年人口数据，分别用常规指数平滑模型ETS（A，A，N）和基于Bootstrap和Bagging的ETS（A，A，N）模型，对老龄人口变化规律进行建模，预测黑龙江省未来5年老龄化人口数，并从提高生育率和减少人口流失两个视角题出了缓解黑龙江人口老龄化问题的建议。

【关键词】Bootstrap;Bagging，;时间序列;指数平滑法;老龄人口

引言

全国第七次人口普查数据表明，我国60岁以上人口占人口总数的13.50%，人口老齡化程度进一步加深。面对我国人口老龄化这一不可逆转的过程，党和政府高度重视，《“十四五”规划纲要》提出，我国要实施积极应对人口老龄化战略，完善公共服务体系，促进人口长期均衡发展。近年来，有很多文章研究人口老龄化问题。黑龙江自2005年进入人口老龄化社会，虽晚于全国时间，但老龄化速度非常快。在此背景下，明确黑龙江人口老龄化趋势，对政策和计划的制定具有前瞻性意义。

Bootstrap法也称为自助重抽样，其基本思想是：样本是从总体中随机抽取的，则包含总体的全部信息，那么不妨就把该样本视为”总体”，进行多次有放回抽样生成一系列经验样本，再对每个经验样本计算统计量，就可以得到统计量的分布，进而用于统计推断。可以证明，在初始样本量足够大且是从总体中随机抽取的情况下，自助重抽样能够无偏接近总体的分布。

时间序列数据可用于预测未来值的数据有限，预测精度很受影响。借助Bootstrap法，可以模拟出很多个具有相似分布的时间序列数据，分别在各个时间序列数据上进行建模并得到多个预测结果，再将多个预测结果按集成学习中的Bagging法合成，得到最终预测，将有效地提高时间序列模型的预测准确性。

Bagging也称为“装袋法”是机器学习的集成学习的一种常用策略，是用“有放回”抽样方式（即Bootstrap法）抽取训练集，对于包含个样本的训练集，进行次有放回的随机抽样操作，得到样本子集（有重复）中有接近36.8%的样本没有被抽到。按照同样的方式重复进行，就可以采集到个包含个样本的数据集，从而训练出个基学习器。最终对这个基学习器的输出进行结合，分类问题就采用“多数决”，回归问题就采用“取平均”。比如随机森林就是自助重抽样若干个子样本，训练多棵CART树，将多个预测结果做“多数决/取平均”得到最终预测，模型性能比CART树有显著的提升。

本文尝试将上述Bootstrap和Bagging思想用于时间序列模型。

1.基于Bootstrap和Bagging时间序列模型

经典的时间序列模型包括：确定性分解（STL）、指数平滑法（ETS）、ARIMA。

按Bootstrap法生成多个相似的时间序列数据，适合结合STL法来用。STL法认为时间序列是受不同影响因素共同影响的叠加效果，故非平稳时间序列可按下式确定性因素进行分解：

其中，为原始时间序列，为趋势部分，为季节部分、为剩余部分。

先对剩余部分进行重洗牌（shuffled）得到自助的剩余序列，因为STL剩余序列中可能存在自相关性，所以不能使用普通的Bootstrap，而是采用“分块Bootstrap”，即不是随机抽样单个值，而是随机抽样时间序列的连续片段，再合并到一起，这样就会保持原来的短期依赖结构。这样得到的Bootstrap剩余序列加上趋势部分和季节部分，再做反向变换就得到与原始时间序列相似的模拟序列。

图1展示了Bootstrap时间序列的一种常用做法分块Bootstrap，需要说明的是，本文并不是直接对原时间序列，而是对其分解的剩余部分做分块Bootstrap.

基于Bootstrap法得到的模拟时间序列，一种用途是提高预测准确性。具体来说，是采用Bagging法思想：从每个时间序列生成预测，并对得到的预测求平均，作为最终预测。这与简单地直接用原始时间序列得到预测相比，可以获得更好的预测。

每个时间序列预测采用指数平滑法建模，指数平滑法包含很多种类，fpp3包中的ETS（）函数能够根据AICc值（小样本偏差做修正的AIC，评估模型好坏的指标）自动选择最优的指数平滑模型，对于本文的老龄人口数据，选出的最优模型是带加法误差的Holt线性趋势模型ETS（A，A，N）：

其中，表示时刻的序列水平，表示时刻的斜率，为平滑系数，

综上，基于Bootstrap和Bagging时间序列模型的算法步骤：

（1）用原始时间序列生成个Bootstrap模拟时间序列

（2）对每个模拟时间序列，分别用ETS（A，A，N）模型建模，得到预测

（3）按Bagging法取平均得到最终预测

2.实证分析

本文使用最新4.1.0版本的R语言软件和专门做时间序列分析的fpp3包（0.4.0）实现。

从《黑龙江统计年鉴》获取1986-2019年黑龙江省的总人口和老龄人口数据（65岁及以上人口数），并计算老龄人口占比，绘制点线图。

由图2可见，黑龙江省的老龄人口和老龄人口占比基本相似的具有明显的逐年上升趋势。2019年黑龙江省老龄人口占比已达到13.75%， 并且没有放缓的趋势，老龄化问题是非常严峻的。

2.1常规指数平滑预测：ETS（A，A，N）模型

先只对原始时间序列自动ETS建模，R代码：

运行结果表明，自动选择ETS（A，A，N）模型，模型的AICc值=270.7287;模型光滑参数估计值; 初始状态值， 预测方差. 带入（2）式就可以得到该时间序列的预测过程：

2.2基于Bootstrap和Bagging的ETS（A，A，N）模型

先用Bootstrap法生成模拟时间序列。以老龄人口数据作为原始时间序列数据，用tsibble（）函数创建为年度时间序列对象，再用model（）+STL（）函数做STL分解，下面给出其图形展示（图3）：

图3的上子图是原始时间序列，中子图是趋势序列，下子图是剩余序列。注意，未包含季节序列，因为原始时间序列没有周期性。

接下来，用generate（）函数实现“分块块Bootstrap法”生成多个自助抽样时间序列，需要提供模拟次数和块长度，并用new_data参数传入原始序列以保持相同时间索引。以块长度为4生成10个抽样时間序列为例，可视化模拟效果（图4）：

黑色曲线是原始时间序列，彩色曲线是模拟的时间序列。本文原始时间序列比较平滑，若原始序列有较多的波动，模拟序列也能很好地模拟相应的波动。

本文采用上述Bootstrap法模拟100个时间序列：

df_stl = model（df， stl = STL（old））   # 先做STL分解

set.seed（123）                   # 让抽样结果可重现

sim = df_stl %>%

generate（new_data = df， times = 100，

bootstrap_block_size = 4） %>%

select（-.model， -old）

接着对这100个模拟序列分别拟合ETS模型，并预测未来5年老龄人口：

ets_forecasts = sim %>%

model（ets = ETS（.sim）） %>%

forecast（h = 5）

得到的结果是未来5年每一年都有100个预测值。

根据Bagging法，对各组100个预测值取平均，得到最终预测：

summarise（ets_forecasts， pre = mean（.mean））

并可视化预测结果（代码略）

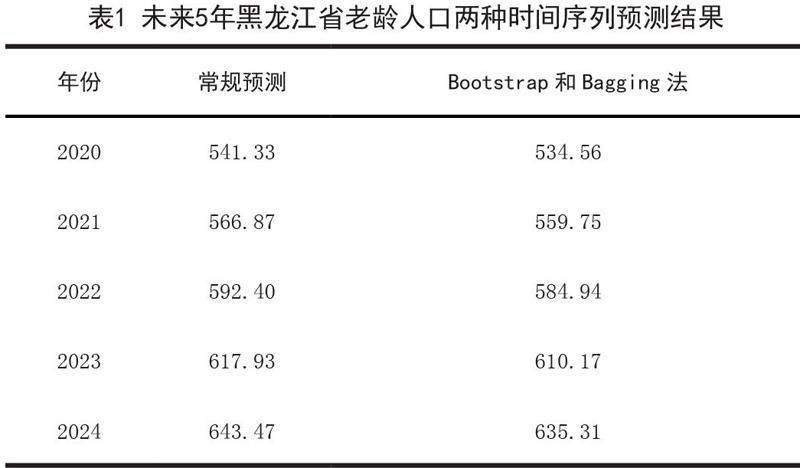
图5中蓝色线为常规ETS（A，A，N）模型预测，红色线为基于Bootstrap和Bagging的ETS（A，A，N）模型预测，蓝色阴影区域为95%和80%置信区间。两种预测方法的结果如表1所示：

3.政策建议

通过对黑龙江省老龄化人口进行实证分析，构建常规指数平滑模型ETS（A，A，N）和基于Bootstrap和Bagging的ETS（A，A，N）模型预测未来5年黑龙江人口老龄化趋势，预测结果表明：未来5年，黑龙江人口老龄化程度将进一步加深，65岁老年人口数将持续稳定上升。

基于此，结合我国基本国情和黑龙江省具体情况，本文提出以下建议：

（1）适度提高生育率，避免产生劳动力短缺。人口老龄化不断加深会造成劳动力供给不足，而适当提高生育水平有助于缓解这一局面。我国已实行“放开二孩”

政策，据此进一步增强政策包容性，推动生育政策与经济社会衔接，可促进政策潜力的释放，改善人口结构，消除人口老龄化带来的负面影响。

（2）充分发挥本地人力资本，避免人口流失。黑龙江省经济发展环境使得人才逐渐流失，适龄劳动力的流失和老年劳动资源的不足，又进一步阻碍了黑龙江省的经济发展。因此，一方面可借鉴发达国家经验，实行弹性退休机制，鼓励退休老人再就业，有效利用老年人力资本;另一方面制定符合本省的人才福利政策，优化产业结构，吸引人才回流，充分发挥人力资本对经济增长的促进作用。（通讯作者：张敬信）

参考文献

[1]王晓峰，张正云.东北地区人力资本问题及其对经济发展的长期影响研究[J].经济纵横，2016（01）：60-64.

[2]都阳，封永刚.人口快速老龄化对经济增长的冲击[J].经济研究，2021，56（02）：71-88.

[3]杜鹏，李龙.新时代中国人口老龄化长期趋势预测[J].中国人民大学学报，2021，35（01）：96-109.

[4]敖荣军，常亮.基于结构方程模型的中国县域人口老龄化影响机制[J].地理学报，2020，75（08）：1572-1584.

[5]张芳，孟昭为.Bootstrap法对时间序列问题预测区间的修正[J].山东理工大学学报（自然科学版），2010，24（04）：12-14.

[6]徐继伟，杨云.集成学习方法：研究综述[J].云南大学学报（自然科学版），2018，40（06）：1082-1092.

[7]Hyndman， R.J.， & Athanasopoulos， G. （2021） Forecasting： principles and practice， 3rd edition， OTexts： Melbourne， Australia. OTexts.com/fpp3.

基金项目：黑龙江省哲学社科青年项目：全面二孩政策对黑龙江省人口的影响及对策研究，项目编号：17TJC134

作者简介：

通讯作者：张敬信（1982-），男，河北保定人，哈尔滨商业大学基础科学学院副教授，基础数学博士，研究方向为数学模型、数据挖掘、人口就业等。

秦蔚瑶（1998-），女，汉族，山西晋城人，研究生，应用统计硕士，研究方向为应用统计。

罗志坤（1984-），男，河南周口人，哈尔滨商业大学基础科学学院讲师，基础数学博士，研究方向为数学模型、商业经济等。