非均匀正弦交流电场液滴介电泳迁移规律研究

孙治谦, 周衍涛, 李 宁, 王振波

非均匀正弦交流电场液滴介电泳迁移规律研究

孙治谦1, 周衍涛2, 李 宁1, 王振波1

(1. 中国石油大学(华东) 新能源学院, 山东 青岛 266580;2. 西安交通大学 能源与动力学院, 陕西 西安 710049)

为了探究非均匀电场下液滴的迁移机制，基于显微观测和数值模拟手段，研究了蜂窝-悬针电极间非均匀正弦交流电场液滴介电泳迁移规律。结果表明，随电压幅值增加，介电泳力增大，液滴速度、加速度、瞬时速度波动幅度和频率均显著增大；随电场频率增加，受液滴极化及驰豫特性的影响，液滴平均速度先增大后减小，电场频率为200 Hz时，平均速度最大；随油品黏度增加，液滴阻力增大，液滴瞬时迁移速度降低至1 mm×s-1；随液滴粒径的增加，液滴荷电量增大，液滴粒径为2 mm时，瞬时速度最高可达3 mm×s-1。液滴速度由于电场变化而随时间呈波动变化，电压幅值和液滴粒径对液滴瞬时速度波动幅度和频率存在显著影响，而电场频率和油相黏度则影响不大。相关结论为高效紧凑电聚结设备的研发及应用提供了理论依据。

电聚结；非均匀电场；介电泳；数值模拟

1 前 言

原油脱水(盐)是石油工业必不可少的预处理工序，主要包括化学法、过滤法、重力沉降法、离心分离法、超声波法、热处理法和电聚结法等[1～4]。其中，电聚结是重要的原油脱水技术，主要依靠水滴间偶极吸引力促进聚并，加速水滴沉降[5]。液滴聚并和电场条件、液滴物性及空间位置等有关。王贞涛等[6]用VOF方法和漏电介质模型模拟了静电场中液滴变形和内部流动。Mohammadi[7]研究了油中液滴在电场作用下的聚并，发现液滴连线与电场线夹角越小，聚结越快。然而，液滴在电场中行为复杂，除了液滴聚并外，还需考虑破碎、迁移和聚并产生的二次液滴等。任瑞娟等[8]研究了不同波形电场下液滴极化变形规律，发现存在使变形度最大的最佳频率。与均匀电场相比，通常认为非均匀电场更为高效。Mhatre等[9]对针-板电极中的液滴群行为展开了研究。陈庆国等[10]研究了非均匀电场中液滴变形和聚并，发现增大非均匀系数能提高液滴聚结速率。陈庆国等[11]采用流场和电场耦合的方法研究了交流电场下的液滴变形，并分析了液滴直径对液滴聚并速率的影响。陈庆国等[12]又通过相场方法研究均匀电场和非均匀电场下液滴的运动特性，发现非均匀电场下的液滴接触机率更大。从以上研究发现，以往对均匀电场的研究较充分，但是对于非均匀电场的研究较匮乏。与均匀电场相比，非均匀电场中，W/O乳状液中的水滴受介电泳力向高场强区域迁移、聚集，从而提高了水滴的聚结效果[13]。基于此，课题组提出一种应用于电脱水(盐)罐中、能产生非均匀电场的蜂窝-悬针电极[14]，并以此为基础，简化得到同轴六边形-圆电极的数值模型，在施加正弦交流电场的条件下，对电极中液滴受介电泳力的迁移运动规律展开探究，分析电场参数和物性参数的影响，为高效紧凑电聚结设备的研发及应用提供理论依据。

2 实验装置与材料

实验装置及流程如图1所示，包括高频脉冲电源、数码显微镜、观测单元等。

图1 实验装置及流程

1. electrocoalescence cell 2. Electrodes 3. microscope 4. transformer 5. Computer 6. power supply 7. light source

高频脉冲电源由中国石油大学(华东)自行研制，电压调节范围：0～9.8 kV，频率调节范围：0.41～6.3 kHz，脉宽比调节范围：0.1～0.875。采用江西凤凰光学仪器集团生产的PH50数码显微镜，拍摄得到的图像经ImageJ软件处理。如图2所示，实验观测单元和数值模型一致，且液滴的运动和观测区域已在图中用圆圈标出。

图2 观测单元

实验中，用微量计量器向蓖麻油中注射一定体积的去离子水，形成一定尺寸的水滴。其中，蓖麻油和去离子水物性如表1所示。

表1 实验材料物性

此外，蓖麻油和去离子水的界面张力为32.20 mN×m-1。

3 模拟方法

3.1 几何模型及边界条件

本研究在COMSOL Multiphysics中建立如图3(a)所示的二维模型，其模型网格划分如图3(b)所示。为了计算的高效和准确，对液滴运动区域进行了网格细化。

由表2可知，油水两相的Clausius-Mossotti系数为0.92，表明液滴向高场强区域运动[15]。此外，为了验证模拟结果的准确性，开展显微实验，并将模拟结果与实验结果进行对比。

图3 几何模型和网格划分

3.2 相场方法

相场模型通过相场变量来得到两相界面的信息，实现对界面的追踪，把表面张力等效为场变量梯度与化学势的乘积，并将其作为体积力的一项加入控制流体压力和速度的Navier-Stokes方程中：

表2 数值模拟中物性参数

相场模型通过4阶偏微分Cahn-Hilliard方程来控制相场变量的演化：

式中：为相场变量；为迁移率，m3×s×kg-1；为化学势，Pa。

3.3 电场和流场耦合

计算区域内电场由Maxwell方程控制：

式中：0为真空介电常数，F×m-1；r为流体相对介电常数；为电场强度，V×m-1。

电场产生电应力E可由Maxwell应力张量推导得到，由式(4)给出：

3.4 液滴位置和速度的确定

如图4和5所示，本研究以液滴在运动方向上的最长截线的中点为液滴中心，并以液滴中心和电极中心的距离表征液滴位置。

图4 液滴中心确定图

图5 液滴位置确定图

图6 实验和模拟结果对比

模拟过程中，每隔0.005 s对解进行一次存储和导出，经后处理后可得到自模拟开始起0、0.005、0.01 s、等时刻液滴位置的数据，进而得到液滴运动速度。

3.5 液滴位置和速度的确定

由图6可知，模拟和单液滴介电泳迁移实验(图7)吻合良好。此外，进行了网格无关性验证，综合计算效率和结果准确性，确定网格密度为430.576 923 1 个×mm-2。

图7 单液滴介电泳迁移

4 结果与讨论

4.1 液滴介电泳运动

模拟得到的液滴在非均匀电场中受介电泳力迁移过程如图8所示。

由图8可知，非均匀电场中，液滴向着电极中心区域运动，受电场力作用拉伸变形。图9给出了电场模拟图，由电场线稀疏可知，越靠近电极中心区域，场强越高。如图10所示，液滴的迁移使原本分散的液滴聚集，缩短了彼此间距离[9]。

图8 液滴在非均匀电场中的介电泳迁移

(potential difference amplitude 30 000 V; frequency 50 Hz; diameter 2.0 mm; viscosity 0.35 Pa×s)

图9 同轴六边形-圆电极电场模拟图

图10 液滴在介电泳力作用的聚集

在非均匀电场中，液滴受到的介电泳力DEP表达式如下[16]：

式(9)给出了理想情况下液滴的介电泳力迁移速度，但实际情况更加复杂。模拟得到的液滴电场力分布如图11所示。

液滴内部电荷受电场作用在液滴表面积累，电场作用于电荷而产生电场力。在垂直于电场方向上，电场力彼此对称、抵消；在平行于电场方向上，靠近电极中心端的电场力大于靠近边缘电极端的电场力，导致了液滴的介电泳迁移运动。由图11可知，电场力随时间的变化呈近似正弦波形，这是液滴迁移致使所处位置变化导致，

图11 液滴两极电场力随时间变化趋势

4.2 电压幅值的影响

正弦交流电场的电压幅值决定了电场强度。模拟计算中，液滴初始位置=15 mm。

由图12(a)可知，液滴瞬时速度随时间波动，速度波动幅度和频率随电压幅值的增大而增大。随着电场强度的增大，电场力增大，导致液滴的速度和加速度增大，速度波动幅度越大[17]。同时，液滴极化状态改变越快，液滴瞬时速度波动频率越大。由图12(b)可知，液滴平均速度随电压幅值增大而增大，这是由于介电泳力随电压幅值增大而增大。此外，由图12(a)可知，液滴瞬时速度随着液滴靠近电极中心而增大，这是因为液滴越靠近电极中心，所受介电泳力越大。

图12 电压幅值对液滴迁移的影响

4.3 频率的影响

正弦交流电场中，液滴极化需要一定的弛豫时间，因此随着电场频率的变化，液滴极化状态随之变化。

由图13(a)与图12(a)对比可知，频率没有像场强那样明显地影响液滴瞬时速度波动的幅度和频率，但仍可发现液滴速度随着其靠近电极中心区域而不断增大。由图13(b)可知，随着频率的增大，液滴平均速度先增大后减小，并在200 Hz附近取得最大值，说明存在最优频率值。在频率较低时，液滴极化充分；随着频率增大，液滴恢复时间缩短，因此能保持较强的极化状态而不减弱；但是随着频率进一步增大，液滴极化时间缩短，液滴极化程度减弱[17]。对脉冲电场中液滴变形的研究也表明存在最优频率值，随着电场频率接近该值，液滴极化程度达到最大，所受电场力达到最大，液滴变形达到最大[18]。电场中拉伸液滴变形的电场力和促使液滴迁移的介电泳力本质相同。

图13 频率对液滴迁移的影响

4.4 油相黏度的影响

黏度是流体重要性质之一，决定了液滴受介电泳力迁移过程中的阻力[17]。

由图14(a)可知，在不同黏度条件下，液滴速度波动的振幅和频率基本一致，这是由于黏度变化对液滴的极化状态和电场力影响微弱，并不会对液滴速度波动的振幅和频率产生显著影响。但由图14(b)可知，随着黏度的增加，液滴整体迁移速度不断下降，这是由于液滴运动过程中所受的阻力增大，抵消了更多的介电泳力，液滴在电场中受到的合力减小，液滴的平均速度降低。在高黏度下，液滴速度小，此时由黏度增大导致的阻力增大不再明显，因此液滴速度的减小趋势也趋于平缓。

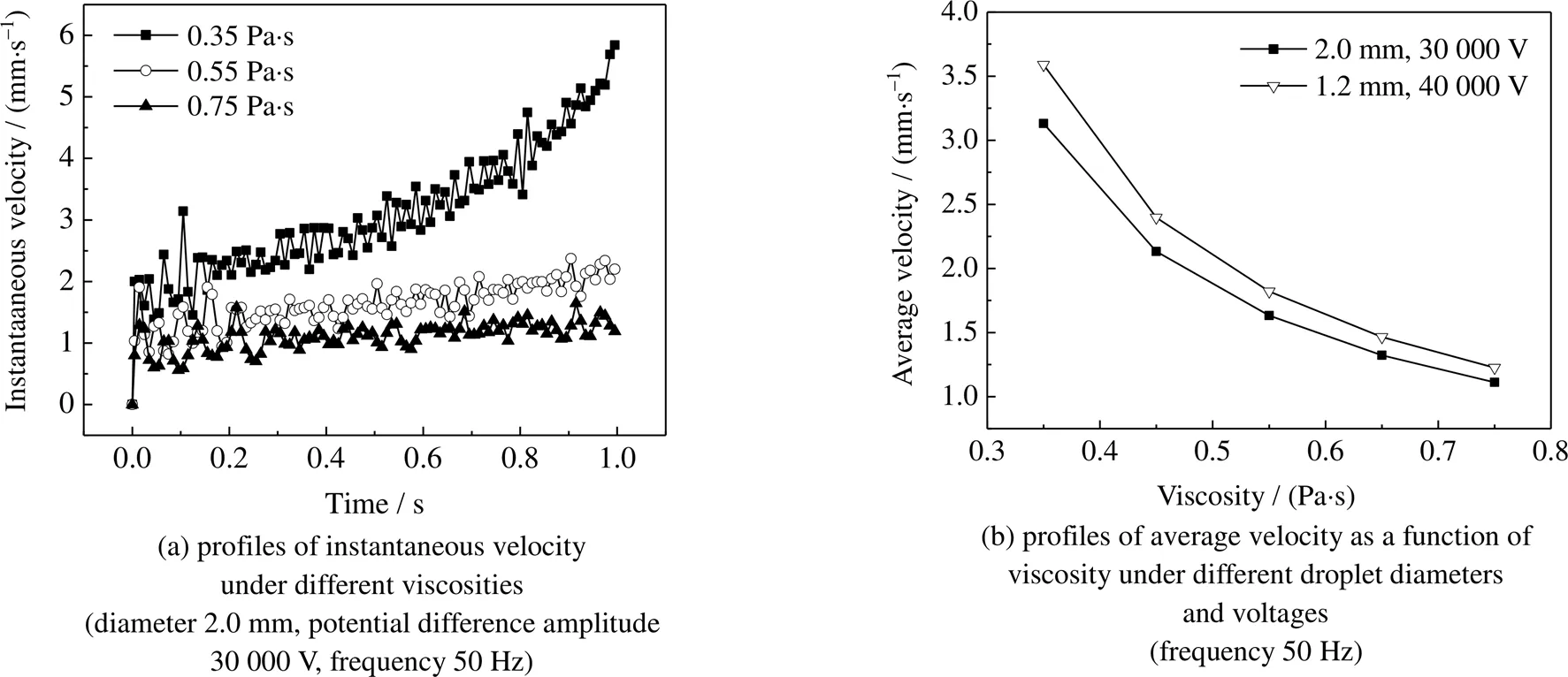
图14 油相黏度对液滴迁移的影响

4.5 粒径的影响

水滴粒径对介电泳的影响如图15所示。

由图15可知，随着液滴粒径的增加，液滴迁移速度增大，这是由于积累在液滴两端的荷电量增加，液滴所受介电泳力增大导致的。因此。由图15(a)可知，液滴瞬时速度波动幅度和频率也随粒径增大，这是由于液滴粒径增大，液滴荷电量增加，电荷对液滴表面膜的冲击性增强，液滴的变形程度增加，导致液滴瞬时速度和频率呈现更明显的周期性振荡特征，其频率接近于电场频率。由图15(b)可知，随着粒径的增加，液滴速度呈现指数增长，这是由于介电泳力增加的速率高于阻力增加的速率，使得液滴加速度不断升高，液滴迁移速度的增速越大。

图15 粒径对液滴迁移的影响

5 结 论

本研究基于COMSOL Multiphysics软件，通过相场方法，模拟了液滴在非均匀正弦交流电场中受介电泳力的迁移运动规律，探究了电压幅值、频率、油相黏度和液滴粒径对液滴迁移速度的影响，主要结论如下：

(1) 非均匀电场中，液滴受介电泳力向电极中心的高场强区域运动，随着液滴靠近中心，迁移速度不断增大，且由于电场强度不断变化，液滴速度呈波动变化。

(2) 在不同电压幅值和液滴粒径条件下，介电泳力占据主导地位，液滴迁移速度随电压幅值和液滴粒径的增大而增加，电压为30 000 V、粒径为2.0 mm时，液滴速度达到最大。在不同连续相黏度条件下，液滴受到的阻力占据主导，随黏度的增加，液滴迁移速度不断减小，在连续相黏度为0.75 Pa×s时，迁移速度最低接近于1 mm×s-1。

(3)随电场频率的增大，迁移速度先增大后减小，频率为200 Hz时迁移速度最大。随着电压幅值和液滴粒径增大，液滴速度波动幅度和频率增大，而电场频率和油相黏度不会对液滴速度波动产生显著的影响。

[1] MOHAMMED R A, BAILE A I, LUCHHAM P F,. Dewatering of crude oil emulsions [J]. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 1994, 83(3): 261-271.

[2] SUN D, JONG S C, DUAN X D,. Demulsification of water-in-oil emulsion by wetting coalescence materials in stirred and packed columns [J]. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 1999, 150(1/2/3): 69-75.

[3] TAYLOR S E. Theory and practice of electrically-enhanced phase separation of water-in-oil emulsion [J]. Transactions of the Institution of Chemical Engineers, 1996, 74(5): 526-540.

[4] HIRATO T, KOYAMA K, TANAKE T,. Demulsification of water-in-oil emulsion by an electrostatic coalescence method [J]. Materials Transactions, JIM, 1991, 32(3): 257-263.

[5] MHATRE S, VIVACQUA V, GHADIRI M,. Electrostatic phase separation: A review [J]. Chemical Engineering Research and Design, 2015, 96: 177-195.

[6] 王贞涛, 董庆铭, 张永辉, 等. 静电场中液滴变形及内部流动的研究 [J]. 高校化学工程学报, 2015, 29(5): 1098-1105.

WANG Z T, DONG Q M, ZHANG Y H,. Droplet deformation and its internal flow in electrostatic field [J]. Journal of Chemical Engineering of Chinese Universities, 2015, 29(5): 1098-1105.

[7] MOHAMMADI M. Numerical and experimental study on electric field driven coalescence of binary falling droplets in oil [J]. Separation and Purification Technology, 2017, 176: 262-276.

[8] 任瑞娟, 李彬, 孙治谦, 等. 不同电场波形下液滴极化变形规律研究 [J]. 化学工程, 2018, 46(7): 51-62.

REN R J, LI B, SUN Z Q,. Investigation on the law of droplet polarization and deformation under different electrical waveforms [J]. Chemical Engineering (China), 2018, 46(7): 51-62.

[9] MHATRE S, THAOKAR R. Pin-plate electrode system for emulsion of a higher conductivity leaky dielectric liquid into a low conductivity medium [J]. Industrial and Engineering Chemical Research, 2014, 53(34): 13488-13496.

[10] 陈庆国, 宋春辉, 梁雯, 等. 非均匀电场下乳化油中液滴变形动力学行为[J]. 化工学报, 2014, 66(3): 955-964.

CHEN Q G, SONG C H, LIANG W,. Kinetics behavior of water droplet deformation in emulsified oil subjected to non-uniform electric field [J]. CIESC Journal, 2014, 66(3): 955-964.

[11] 陈庆国, 郑天宇, 梁雯, 等. 交流电场下液滴形变及聚结影响因素分析 [J]. 电机与控制学报, 2015, 19(11): 51-58.

CHEN Q G, ZHENG T Y, LIANG W,. Analysis of influencing factors for droplets deformation and coalescence in AC electric field [J].Electric Machines and Control, 2015, 19(11): 51-58.

[12] 陈庆国, 宋春辉, 梁雯, 等. 非均匀和均匀电场下液滴的形变及运动行为 [J]. 高电压技术, 2016, 42(3): 949-958.

CHEN Q, SONG C, LIANG W,. Deformation and motion behavior of water droplet under uniform and non-uniform electric field [J]. High Voltage Engineering, 2016, 42(3): 949-958.

[13] EOW J S, GHADIRI M, SHARIF A O,. Electrostatic enhancement of coalescence of water droplets in oil: A review of the current understanding [J]. Chemical Engineering Journal, 2001, 84(3): 173-192.

[14] 孙治谦, 周衍涛, 王振波, 等. 一种高效电脱水器: CN108949223A [P]. 2018-12-07.

SUN Z Q, ZHOU Y T, WANG Z B,. One kind of high-efficiency electric dehydrator: CN108949223A [P]. 2018-12-07.

[15] JONES T B. Basic theory of dielectrophoresis and electrorotation [J]. IEEE Engineering in Medicine & Biology Magazine the Quarterly Magazine, 2003, 22(6): 33-42.

[16] MOLLA S H, MASLIYAH J H, BHATTACHARJEE S. Simulations of a dielectrophoretic membrane filtration process for removal of water droplets from water-in-oil emulsions [J]. Journal of Colloid and Interface Science, 2005, 287(1): 338-350.

[17] KAVEHPOUR H P. Coalescence of drops [J]. Annual Review of Fluid Mechanics, 2015, 47(1): 245-268.

[18] LI B, VIVACQUA V, GHADIRI M,. Droplet deformation under pulsatile electric fields [J]. Chemical Engineering Research and Design, 2017, 127: 180-188.

Investigation of droplet dielectrophoresis movement under non-uniform AC electric fields

SUN Zhi-qian1, ZHOU Yan-tao2, LI Ning1, WANG Zhen-bo1

(1. College of New Energy, China University of Petroleum (East China), Qingdao 266580, China;2. School of Energy and Power Engineering, Xi'an Jiaotong University, Xi'an 710049, China)

Based on microscopic observation and numerical simulation, mechanism of droplet dielectrophoresis movement under non-uniform sinusoidal AC electric fields between honeycomb and suspended needle electrodes was studied.The results show that as voltage amplitude increases, dielectrophoretic force, velocity, droplet acceleration, fluctuation amplitude and frequency of instantaneous velocity all increase significantly. The average droplet velocity increased and then decreased with the increase of electric field frequency due to the influence of polarization and relaxation of droplet.The average velocity was the highest when the electric field frequency was 200 Hz. The resisting force increased with the increase of oil viscosity, and the transient migration velocity of droplet decreased to 1 mm×s-1.With the increase of droplet diameter, the charge quantity of droplet increased, and the instantaneous velocity can reach as high as 3 mm×s-1when the droplet size was 2 mm.Droplet velocity fluctuated due to the change of electric field. Voltage amplitude and droplet size had significant effects on the fluctuation amplitude and frequency of instantaneous velocity, while electric field frequency and oil viscosity had few effects.These results can provide theoretical guidance for the design of efficient and compact electrocoalescer.

electrocoalescence; non-uniform electric field; dielectrophoresis; numerical simulation

TQ 028.4

A

10.3969/j.issn.1003-9015.2021.03.010

1003-9015(2021)03-0464-07

2020-07-12；

2020-12-26。

山东省自然科学基金(ZR2020MB137)；山东省重大科技创新工程项目(2019JZZY010508)；国家自然科学基金(21406267)；中央高校基本科研业务费专项资金 (18CX02122A)。

孙治谦(1983-)，男，山东青岛人，中国石油大学(华东)副教授，博士。

王振波，E-mail：wangzhb@upc.edu.cn