采用非线性流量特性补偿的直驱式变转速泵控系统轨迹跟踪控制

赫连勃勃，吕立彤，陈 正，3，姚 斌，4

(1.浙江大学流体动力与机电系统国家重点实验室，浙江杭州 310027；2.石家庄铁道大学机械工程学院，河北石家庄050043； 3.浙江大学海洋学院，浙江舟山 316021；4.普渡大学机械工程学院，美国西拉法叶IN47907 )

引言

作为一种从动力源头考虑功率匹配的全局型节能动力系统，变转速泵控系统(变频液压系统)具有无节流能量损失的优点[1]，可在源头实现液压系统的节能。但是传统泵控系统往往具有响应慢、精度低的缺点，限制了其在精密轨迹跟踪场合的应用。

近年来，变转速电机-泵直驱电液系统的发展与伺服技术[2]的提升使得泵控系统在保留高能效特性的同时，具有更高的硬件集成度和更快的响应速度，为泵控液压缸系统的精确运动轨迹跟踪提供了硬件基础。

变转速泵控系统在实际应用中存在系统动力学阶数高、非线性强等控制难点，且此类系统依旧存在泵的流量非线性、流量偏差大等问题，使其难以完成高精度的执行器运动轨迹跟踪。因此，需要基于液压系统非线性动力学模型进行控制策略设计，利用系统的实时状态反馈处理模型的非线性与不确定性，从而实现高精度的轨迹跟踪。

在国内外液压系统控制策略研究成果中，KANG R等[3]建立了电静液作动器(Electro-Hydraulic Actuator，EHA)的准确数学模型；LIN Y等[4]针对EHA提出一种泵控系统的离散滑模控制策略，保证了系统在变摩擦力影响下的较高控制精度；AHN K K等[5]提出了一种自适应反演位置控制方案，着重通过在线参数自适应的方式处理伺服电机-泵控制系统的参数不确定性；HELIAN B等[6]将泵控系统研究中通常忽略的伺服电机-泵高阶动力学考虑到系统运动控制器设计中，处理非线性和不确定性等问题，改善了系统运动控制精度；LYU L等[7]提出一种泵阀结合的液压缸进出口独立控制系统，以此实现液压系统高精度、高能效的控制目标。

上述研究工作能够为本研究追求高精度运动控制目标提供借鉴，但大部分研究均未充分考虑液压泵的流量偏差等变转速泵控系统特有的非线性特性，不能满足变转速泵控液压缸系统的精确轨迹跟踪需求。因此，为实现直驱泵控电液系统高精度轨迹跟踪(运动控制)，还需要根据其系统特点制定控制策略。

为实现直驱变转速泵控伺服电液系统的高能效高精度控制，本研究开展泵控直驱电液伺服系统关键控制技术研究，充分利用直驱泵控系统没有节流损失、高能效的优点，同时针对泵控系统在各个工况下产生的诸如模型非线性、参数不确定性等控制难点，设计基于模型的控制策略以实现泵控直驱电液伺服系统的高性能控制。

本研究在对泵控液压缸系统中存在的非线性进行综合分析的基础上，进行整个系统的有效建模。基于直驱式变转速泵控液压缸的系统，设计ARCB控制器，以解决液压系统的高阶动力学、非线性、不确定性等控制难点[8]。本研究中的ARCB控制器设计由两步组成，包括运动轨迹跟踪环、压力流量环，以此来完成高阶系统的控制器设计。反演控制器的每一环节中都有自适应鲁棒控制设计。此外，基于变转速泵控系统的流量偏移问题，提出一种非线性泵流量映射方案来处理特定的泵流量偏差。基于先验数据对泵的流量模型进行映射，使得映射的数据模型可以准确描述变转速泵在不同转速、压强下的流量非线性；同时，将映射数据模型与基于压力的实时自适应泄漏参数相结合，使得流量模型在控制器设计中兼具自适应性，可以在实时系统实现更好的模型补偿。试验表明，本研究提出的控制策略可有效解决泵的流量偏差问题，在液压缸执行器不同速度下均可实现理想的轨迹跟踪精度。

1 动力学建模与流量映射策略

本研究的液压系统为典型的开式回路伺服直驱系统[6]，液压缸执行器由变转速定量泵直接驱动，由电磁换向阀来改变液压缸活塞的运动方向。

液压缸的的动力学方程：

(1)

式中，m—— 惯性负载质量

xL—— 液压缸位移

b—— 黏性摩擦系数[9]

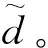
液压系统的压力流量动力学方程[10]：

(2)

(3)

式中，βe—— 有效弹性模量

Ci—— 液压缸内泄漏系数

Q1,Q2—— 分别为液压缸两腔流量(流速)

V1，V2液压缸两腔容积，可被表示为：

V1=V01+A1xL

(4)

V2=V02-A2xL

(5)

式中，V01，V02—— 分别为两腔初始容积

电机的转速动力学可描述为：

(6)

式中，J—— 电机转子转动惯量

T，TL—— 分别为输入扭矩和负载扭矩

bf—— 电机摩擦系数

由于在变转速伺服泵控液压系统中，伺服电机的动态性能较好，响应速度快，其闭环频宽通常远大于液压系统的其他环节。所以将电机转速动力学视为高频动力学，原公式即可简化为静态方程：

ω=kmu

其中，km为伺服电机速度模式下的输入系数。

变转速泵的流量很容易受到压力变化的影响，变得非线性，因此，提出了一种描述泵流量非线性特性的映射方法。为了使流量映射准确、实用，让泵在可变的速度和压力下工作，以收集丰富的数据，包括泵出口压力ps、输入电压u(与转速成比例)和泵流量Qp，并对得到的数据进行曲线拟合。为了正确拟合映射，并且抑制无效数据和噪声干扰的影响，采用薄板样条插值法对泵流量映射进行拟合，从而得到精确的泵源流量数据模型f(QLd,ps)，实现了泵控液压源的精确流量模型的建立。

不同于传统的完全基于先验数据的流量映射方法[11-12]，本研究将得到的非线性映射模型与基于压力的可被实时自适应的参数化模型相结合，使得流量模型在控制器设计中兼具自适应性，可以在实时系统根据实际工况改变，实现更好的模型补偿。同时，流量模型连续，也弥补了分段式模型补偿的缺点。最终，变转速定量泵的流量模型如下所示：

Qp=f(QLd,ps)+Ce(ps-pr)

(7)

流量模型中，f(QLd,ps)为基于实验数据建立的三维非线性映射，映射如图1所示；Ce(ps-pr)为线性流量误差映射，以此补偿先验非线性流量映射的误差；Ce为线性建模误差补偿系数；pr为油箱压力。

2 ARCB控制策略

基于直驱式变转速泵控液压缸的系统，设计ARCB控制器，以解决液压系统的高阶动力学、非线性、不确定性等控制难点。ARCB控制器由2个部分组成，包括运动轨迹跟踪环与压力流量控制环，以此来完成高阶系统的控制器设计。对反演控制器的每一环节进行了自适应鲁棒控制(Adaptive Robust Controller，ARC)设计[13]，如图2所示。

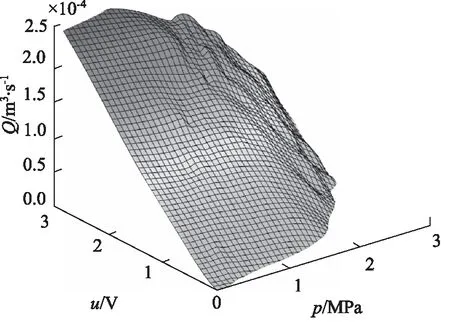
图1 泵流量三维映射

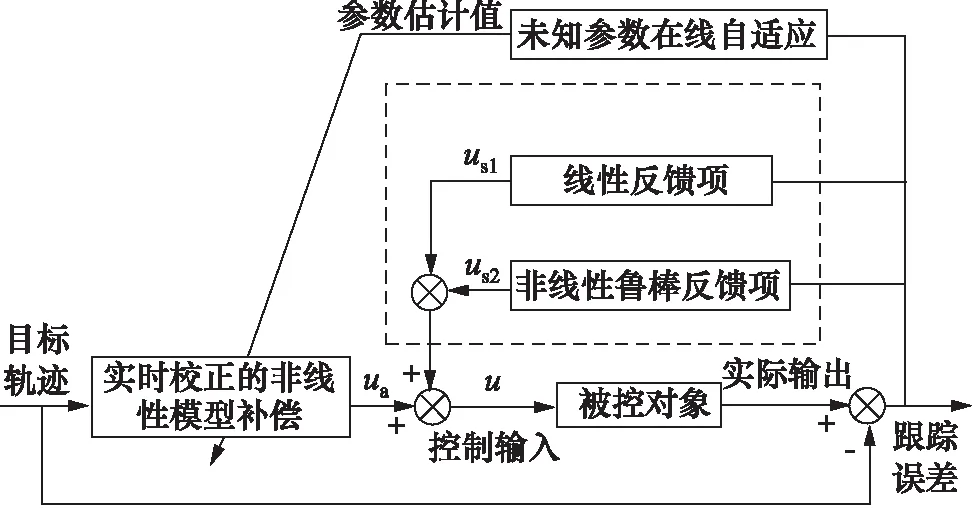
图2 ARC框图

2.1 不确定参数自适应率设计

充分考虑液压系统的模型参数不确定性，包括负载质量m、摩擦系数b、有效弹性模量βe、泄漏系数Ci，Ce，以及不确定干扰分量dn。定义不确定参数集合为θ=[θ1,θ2,θ3,θ4,θ5,θ6]T，其中θ1=1/m,θ2=b/m,θ3=dn/m,θ4=βe,θ5=βeCi,θ6=βeCe。

设计投影式自适应律为：

(8)

其中，θimax与θimin分别为自适应参数的上界与下界；Γ为正定自适应矩阵；τ为自适应函数，将给出其具体设计。

式(8)中，参数自适应率可对不确定参数在线自适应，使得模型补偿更加有效缩小跟踪误差，实现精确轨迹跟踪[10]。

2.2 ARCB控制器设计

1) 步骤一

定义轨迹跟踪误差为z1=x1-xd(t)，以及类滑模变量z2如下：

(9)

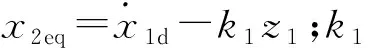
由于G(s)=z1(s)/z2(s)=1/(s+k1)为稳定的传递函数，所以当z2很小或者趋于0时，z1也就会很小或者趋于0。因此，控制器设计目标为使z2尽可能趋近于0。

定义执行器推力FL=p1A1-p2A2为第一步的虚拟输入，设计自适应鲁棒控制器，推导出理想负载力FLd实现精确轨迹位置跟踪(即xd→xL)。

误差动力学可描述为：

(10)

根据误差动力学中的参数不确定性与模型非线性，设计自适应鲁棒控制输入FLd为：

FLd=FLda+FLds

(11)

(12)

(13)

其中，FLda为模型补偿项；FLds为鲁棒反馈项，k2>0为线性反馈增益，FLds2为非线性反馈项，满足以下2个条件：

(14)

其中，ε2>0，是一个任意小的参数。

步骤一的自适应函数与回归量设计如下：

(15)

2) 步骤二

定义z3=FL-FLd为第一步的输入误差，定义泵的有效流量Qd为第二步的虚拟输入，设计自适应鲁棒控制输入QLd使得z3趋近于0或极小值。误差z3的动力学可描述为：

(16)

其中，

(17)

(18)

根据步骤二中误差动力学的参数不确定性与模型非线性，设计自适应鲁棒控制输入QLd为：

(19)

(20)

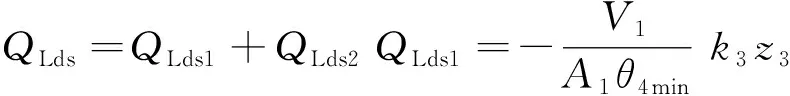
(21)

其中，QLda为模型补偿项，QLds为鲁棒反馈项，k3>0为线性反馈增益，QLds2为非线性反馈项，满足以下条件：

(22)

其中，ε3>0，是1个任意小的参数。

步骤二的自适应函数设计如下：

τ3=τ2+φ3z3

(23)

(24)

基于以上2个步骤得到的理想泵控流量QLd以及通过对式(7)泵流量映射函数反算与根据实时泵出口压力ps反馈，可以得到泵的电信号输入为:

u=f-1(QLd,ps)

(25)

3 试验结果与分析

本研究搭建变转速伺服泵控液压缸系统试验台，对提出的控制策略进行试验验证。

试验台液压站主要由PGF3内啮合齿轮泵与永磁同步交流伺服电机ISMG1组成。液压缸活塞两端直径分别50 mm, 36 mm，并连接280 kg惯性负载。为验证提出控制策略的有效性与适用性，试验分别对2个理想轨迹进行跟踪，分别为慢加速轨迹C1(t)以及快加速轨迹C2(t)，参考轨迹具体参数如表1所示。

两组参考轨迹均为高阶曲线，轨迹曲线如图3所示。

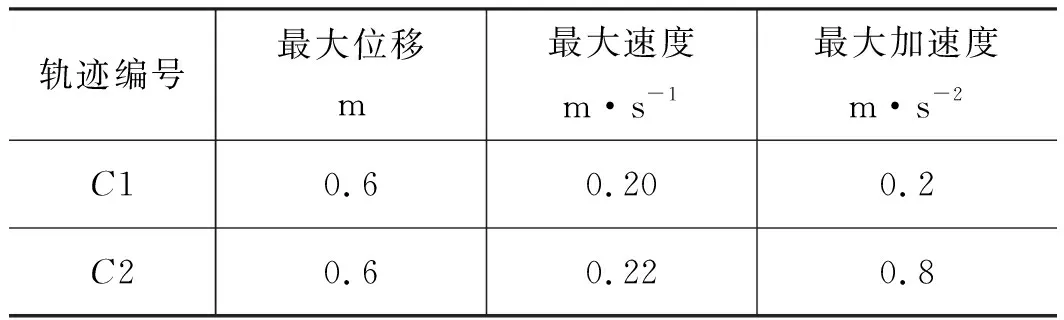
表1 参考轨迹参数

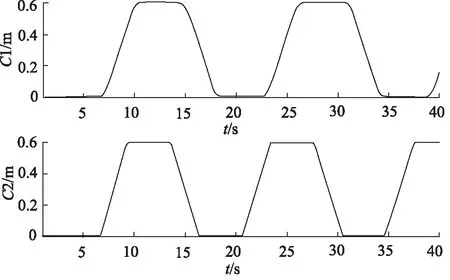
图3 参考轨迹

轨迹误差如图4所示。从图中可得，本研究所提出的控制策略可实现精确的轨迹跟踪精度。不管是慢加速轨迹C1跟踪，还是快加速轨迹C2跟踪，控制器都实现了理想的较小跟踪误差，表明本研究所提出的控制策略可以很好地处理液压系统的高阶动力学、模型非线性与参数不确定性。所提出的变转速定量泵出口流量映射模型可以精确描述实际流量非线性，从而实现精确液压源的流量输出。伺服泵的电信号控制输入(与转速成比例)如图5所示，其中4个不确定模型参数的物理意义分别为θ1=1/m,θ2=b/m,θ3=dn/m,θ6=βeCe。自适应率根据每个步骤的实时误差来改变不确定参数的估计值，并带入模型补偿，使其更加精确有效，以此使得误差收敛至最小值。

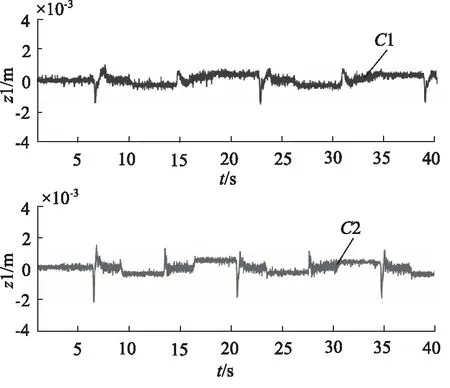
图4 轨迹跟踪误差

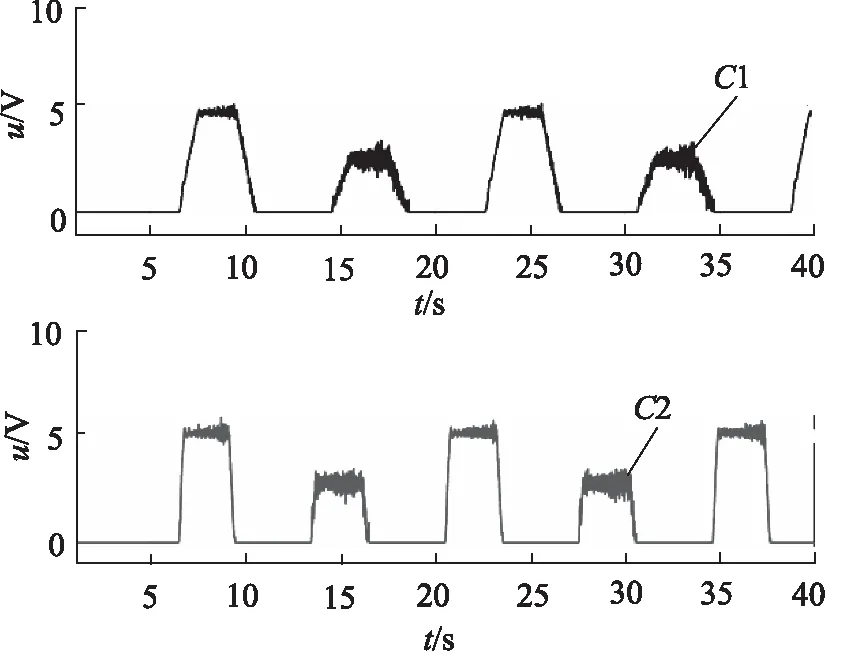
图5 控制输入信号

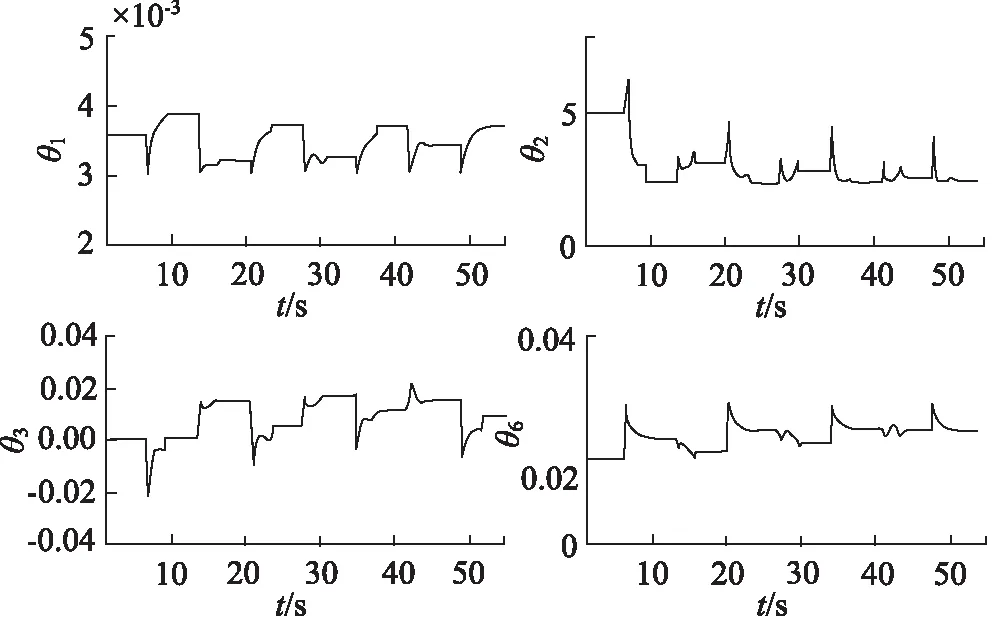
图6 参数自适应曲线

本研究提出的自适应鲁棒反演控制器对泵控液压系统高阶动力学中的不确定参数进行实时参数自适应，C1轨迹跟踪得到关键参数的自适应曲线如图6所示。自适应率根据每个步骤的实时误差来改变不确定参数的估计值，并带入模型补偿，使得模型补偿更加精确有效，以此使得误差收敛至最小值。

4 结论

本研究为实现直驱伺服泵控电液系统精确轨迹跟踪，基于非线性动力学和不确定参数提出了一种自适应鲁棒反演控制策略，同时通过试验拟合了泵的非线性流量特性，并将非线性映射模型与基于压力的可被实时自适应的参数化模型相结合，保证了在定排量泵在实时工况下的精确流量输出。试验结果表明，本研究提出的控制策略可实现液压缸精确轨迹跟踪。