含缺陷空间变异性岩体裂纹扩展的近场动力学模拟*

仉文岗 孟凡胜 卢志堂 何昌杰 李建新 文海家

(①重庆大学土木工程学院， 重庆 400045， 中国)(②重庆大学山地城镇建设与新技术教育部重点实验室， 重庆 400045， 中国)(③重庆大学库区环境地质灾害防治国家地方联合工程研究中心， 重庆 400045， 中国)(④合肥工业大学资源与环境工程学院， 合肥 230009， 中国)(⑤中国建筑第五工程局有限公司， 长沙 410004， 中国)(⑥中建五局第三建设有限公司， 长沙 410004， 中国)

0 引 言

三峡库区分布着大量的岩质边坡，边坡岩体结构复杂，内部含有裂纹孔隙等原始缺陷(王成等， 2004； 汤明高等， 2019； 周家文等， 2019)。岩体结构面作为岩体的重要组成部分，其存在不仅破坏了岩体完整性，而且对岩体的强度和变形破坏具有很大影响(兰恒星等， 2019； 赵海军等， 2019； Chen et al.，2020)。岩体破坏的外因是外部荷载扰动导致岩体屈服，内因则是内部裂纹的萌生、扩展、贯通导致岩体承载力下降。因此对于含缺陷岩体的裂纹发展过程，从细观力学角度对其受力变形和损伤演化过程进行研究，将其与岩石宏观断裂力学机制联系起来，是当今岩石力学与工程领域的重点问题，对于库岸岩体边坡稳定分析也具有十分重要的现实意义(赵程等， 2015)。

长期以来，许多学者对含缺陷岩体的损伤破坏进行了研究，其中包括理论分析，模型试验，数值模拟等方法。目前理论发展尚不完全成熟，模型试验成本较高且含缺陷试样制作复杂，因此数值模拟方法得到了更广泛的应用(蒋明镜等， 2014； 王洪建等， 2015； 陈鹏宇， 2018)。而在数值模拟方法中，有限元法会遇到裂纹尖端奇异性的问题，扩展有限元法在模拟不连续变形时需要引入外部准则，离散元法在模拟连续区域时不能反映连续变化的特点。由于含缺陷岩体材料兼有连续区域与非连续区域，使得大多数数值模拟方法难以满足要求。Silling教授提出的近场动力学方法(Peridynamics， PD)较好地解决了这个问题(Silling， 2000)。近场动力学理论基于非局部作用思想，采用空间积分进行物质内部作用的描述。它兼有无网格方法和分子动力学的优点，相比其他方法，该方法对于微观与宏观、连续与非连续的力学行为具有统一的表述，在数值方面具有无网格属性和不连续求解功能。因此对于兼有连续性与非连续性的含缺陷岩体材料，该方法具有很大的适用性。Yang et al. (2020)利用基于状态的近场动力学模型研究了含非直线预制裂隙的红砂岩试样在不同裂隙角下的断裂行为。马鹏飞等(2019)基于改进的近场动力学模型，对含单裂缝试样在拉伸荷载条件下的裂纹发展过程进行了模拟。李铮等(2019)通过5个不同的数值算例说明了近场动力学算法在处理脆性岩体材料断裂问题方面的有效性和准确性。卢志堂等(2016)提出了近场动力学和有限差分的联合算法，并通过对比证明了该方法在模拟岩体层裂破坏的优越性。然而在利用近场动力学方法模拟岩体裂纹发展的文献中，考虑岩体材料空间变异性的还几乎没有。

岩土体在形成的历史过程中由于地质环境及物理化学作用的不同，在不同的空间位置处会表现出空间变异性。大量研究表明岩土体空间变异性对边坡，基坑，隧道等各类建筑物的稳定性有重大影响。如Liu et al. (2019)采用蒙特卡洛模拟结合极限平衡法和材料点法研究了岩土体空间变异性边坡变形过程中多种破坏模式的发生和演化过程，并且强调了真实岩土体空间变异性数据的价值。黄广龙等(2010)研究发现采用可靠度指标评价基坑整体稳定性比安全系数更为合理，并且可靠度指标受黏聚力、内摩擦角及支护桩嵌固深度变异性的影响较大。王长虹等(2018)将随机场理论引入盾构隧道地表沉降的可靠度指标分析中，发现与随机变量模型相比，基于随机场理论的模型可以得到更精确的可靠指标以优化隧道设计。最近也有学者开始考虑空间变异性对岩体自身变形损伤方面的影响，提出了一种结合随机场理论和离散元方法的概率随机离散元分析(RDEA)方法，研究单轴压缩下岩石碎裂的机理(Zhao et al.， 2020)。但总体来说，考虑空间变异性对岩体失效及裂纹发展影响的研究还很少。

本文采用了一种随机近场动力学方法(RPD)来模拟单轴压缩下含缺陷岩体裂纹的发展。用近场动力学方法模拟岩体裂纹发展过程，随机场方法表征岩体材料的空间变异性。以二维含预制单裂缝矩形岩体试样为例，对计算程序进行了准确性验证，并比较了不同预制裂缝角度后续裂纹的发展情况。最后通过随机场统计参数的变化，重点研究了空间变异性对后续裂纹发展的影响，所得结论可为库区裂隙岩体稳定性分析提供一定参考价值。

1 理论方法及程序验证

1.1 近场动力学理论

1.1.1 基本理论概述

2000年，由美国Sandia实验室的Silling教授提出了近场动力学方法的基本思想。近场动力学经过多年的发展已形成以键为基础、普通状态为基础与非普通状态为基础等多种分支(朱其志等， 2016)，本文仅考虑以键为基础的近场动力学。如图1所示，某物体占据空间域R，假设某一时刻t，空间内任一物质点x与其周围空间一定半径范围内的其他物质点x′之间存在着相互作用，这种相互作用称为键，即质点之间的力通过键传递，若相互作用力为f，则

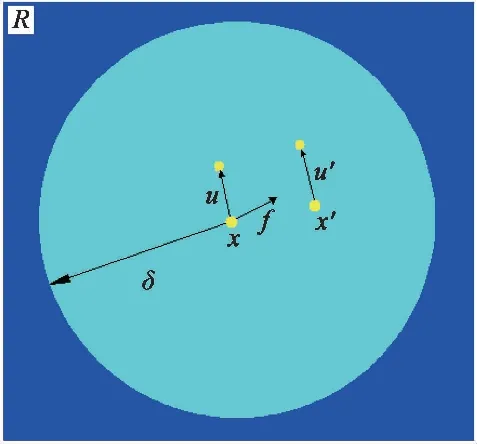
图1 物质点间相互作用

f=f(x，x′，u(x，t)，u(x′，t)t)

(1)

式中：u为物质点位移。

一个物质点的运动状态是外力和其近场范围内所有物质点共同作用的结果，则根据牛顿第二定律可得到质点x的运动方程为

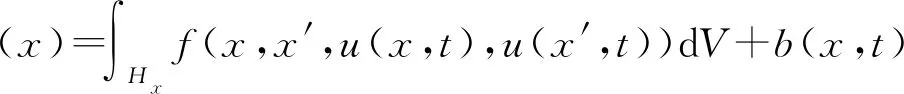
(2)

式中：ρ为物质密度；b为单位体积物质所受的外载荷；Hx为质点x的近场域范围，可用下式表示：

Hx=H(x，δ)={x′-x≤δ|x′∈δ}

(3)

式中：δ为近场域半径。

质点的位置矢量为：

ξ=x′-x

(4)

t时刻质点的位移矢量为：

η=u′(x′，t)-u(x，t)

(5)

则质点之间力的表达式可简化为：

f=f(x，x′，u(x，t)，u(x′，t)，t)=f(η，ξ)

(6)

为了区分力的方向并且将其推广到物体内的任意质点，可定义质点间的力为：

(7)

对于线弹性材料，f(η，ξ)为键的微观弹性应变能密度ω对该键相对位移矢量η的导数：

(8)

键的微观弹性应变能密度为：

(9)

键的伸长率为：

(10)

所以可得基于键的近场动力学模型的本构函数：

(11)

式中：c为微观模量；μ为表征键的连接状态的特征函数； |η+ξ|与|ξ|分别为键变形后的长度与初始长度。

1.1.2 本构关系

与传统理论类似，PD 本构关系也是物质力的状态和变形状态之间的关系，并且PD本构关系中材料参数可以由传统本构关系中材料参数推导得出。在二维平面应力问题中，PD本构函数中微观模量c与传统本构函数中杨氏模量E存在关系式：

(12)

需要注意的是在PD中，材料的泊松比被限定为ν=1/3(Huang et al.，2015)。

在传统本构模型中，对于弹脆性材料，当应力到达峰值时材料突然破坏，因此可将PD本构函数中的特征函数μ定义为：

(13)

式中：s0为极限伸长率，即键断裂的临界变形值，当键的变形超过临界变形值，键断裂且不再传递荷载。

对于二维平面应力问题，键的极限伸长率为：

(14)

式中：G0为物质点的能量释放率。

因此通过键的断裂情形，可以定义物质点的非局部损伤参数，即表征物质点的损伤情况：

(15)

可见近场动力学方法本身就存在破坏准则，不需要再引入其他准则来判断材料是否发生破坏。

1.2 随机场理论

Vanmarcke(1997)率先将随机场方法引入岩土工程可靠度领域。随机场是一个描述空间变异性的概率模型，可以用均值、标准差、自相关函数和波动范围等予以描述。大量研究表明，空间任意两点岩土体间存在着自相关性和变异性。由于岩土工程中现场试验数据的有限性，基于这些数据难以建立起表征岩土体参数自相关性的自相关函数，因此一般选择采用理论自相关函数来近似代替真实自相关函数。另一方面，岩土体参数大多数遵循非高斯分布，并且基于乔列斯基分解的中点法在模拟非高斯随机场中易于理解，便于编程实现。

因此本文采用基于乔列斯基分解的中点法模拟相关非高斯随机场(蒋水华等， 2014)，对数正态变量m的随机场，表达式如下所示：

Rm(x，y)=exp[μlnm+σlnm·Gm(x，y)]

(16)

式中：μlnm和σlnm分别为变量lnm的均值和标准差；Gm(x，y)为正态分布随机场，可通过下式实现：

(17)

式中：n为参数随机场数目；Zk为独立标准正态随机样本矩阵；L为乔列斯基分解计算的三角矩阵，如下所示：

L×LT=C

(18)

(19)

式中：C为相关矩阵，τxij=|xi-yj| 和τyij=|yi-yj|分别为空间任意两点间的水平和垂直方向相对距离。

采用的二维指数型自相关函数，表达式如下所示：

(20)

式中：δh和δv分别为水平和竖直方向的波动范围，波动范围越大，表示参数的空间自相关程度越强。由式(20)可知自相关函数ρ(τx，τy)只与空间两点间的相对距离有关，与两点绝对位置无关。

1.3 程序验证

本文利用MATLAB进行编程，对Wang et al. (2017)中含单裂缝模型在单轴压缩条件下的裂纹扩展过程进行了模拟。如图2所示，矩形试样高150mm，宽75mm，试样中心包含一长为12.7mm，宽为1.27mm的缺陷，缺陷是通过删除该处材料点来实现的。将模型简化为二维平面应力问题，并进行离散化处理。离散近场动力学材料点间距为dx=0.83mm，影响域半径为3.015dx，在试样上下端部设置限制侧向位移的端部约束条件，然后施加速度边界条件，通过改变最外层物质点的速度，将边界条件通过键的作用逐渐传递给材料区域内的所有物质点，采用自适应动态松弛方法进行时间积分，从而实现单轴压缩的模拟过程。假定岩体试样为弹脆性材料，各参数取表1材料均值，当预制裂缝倾角为45°时，模拟结果如图3所示。首先在预制裂缝尖端出现损伤，然后裂纹朝向两端发展，而由于在上下端部存在约束，使得裂纹最终没有朝向最大压应力方向扩展，但总体来说模拟结果与原文献基本一致，包括起裂角度，初始扩展路径等。因此认为本文采用的近场动力学计算程序在模拟岩体裂纹发展方面是适用的。

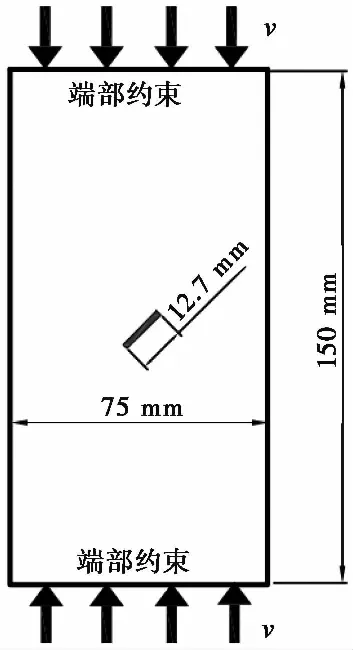
图2 单轴压缩下含单一缺陷岩体试样

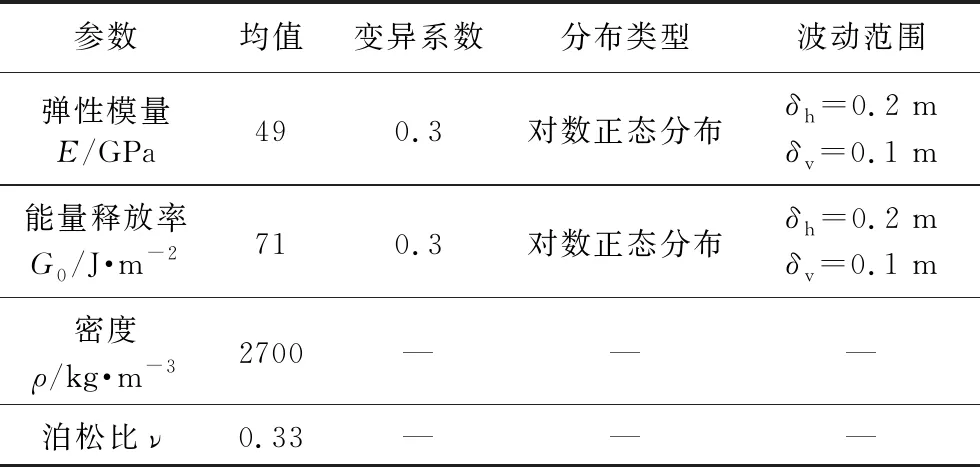
表1 岩体试样力学参数

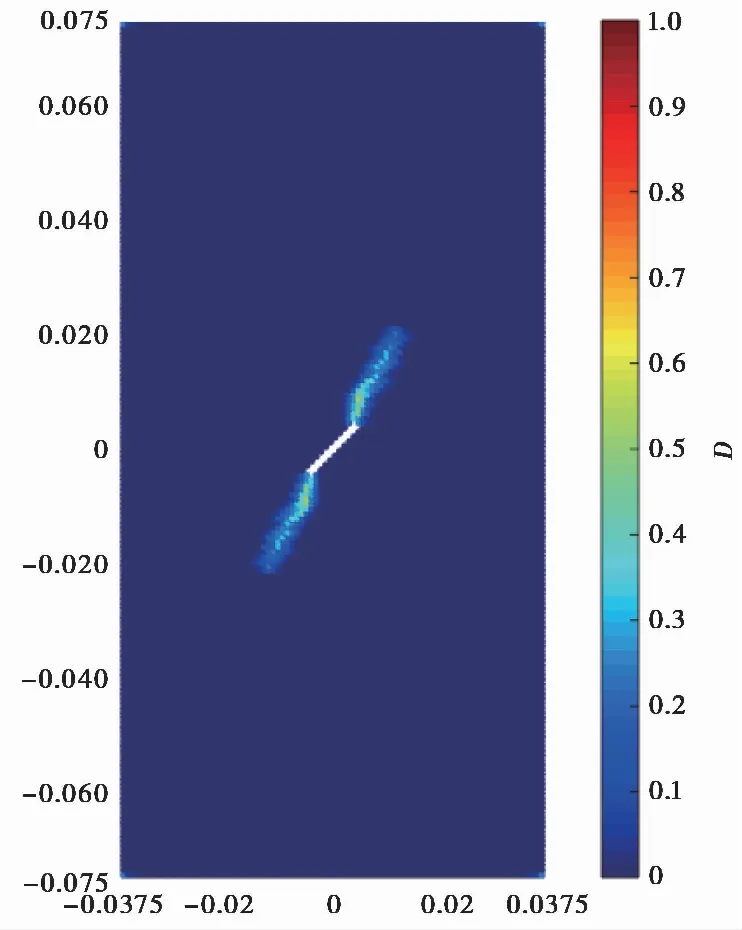
图3 近场动力学模拟结果

为了模拟岩体试件的空间变异性，基于随机场理论，利用MATLAB编程，将弹性模量E和能量释放率G0定义为随机场变量，统计特性参数如表1所示。当水平波动范围δh分别为0.10m和1.00m时，弹性模量E的随机场分布如图4所示，可见本文所用随机场程序可以较好实现岩体试样的空间变异性。

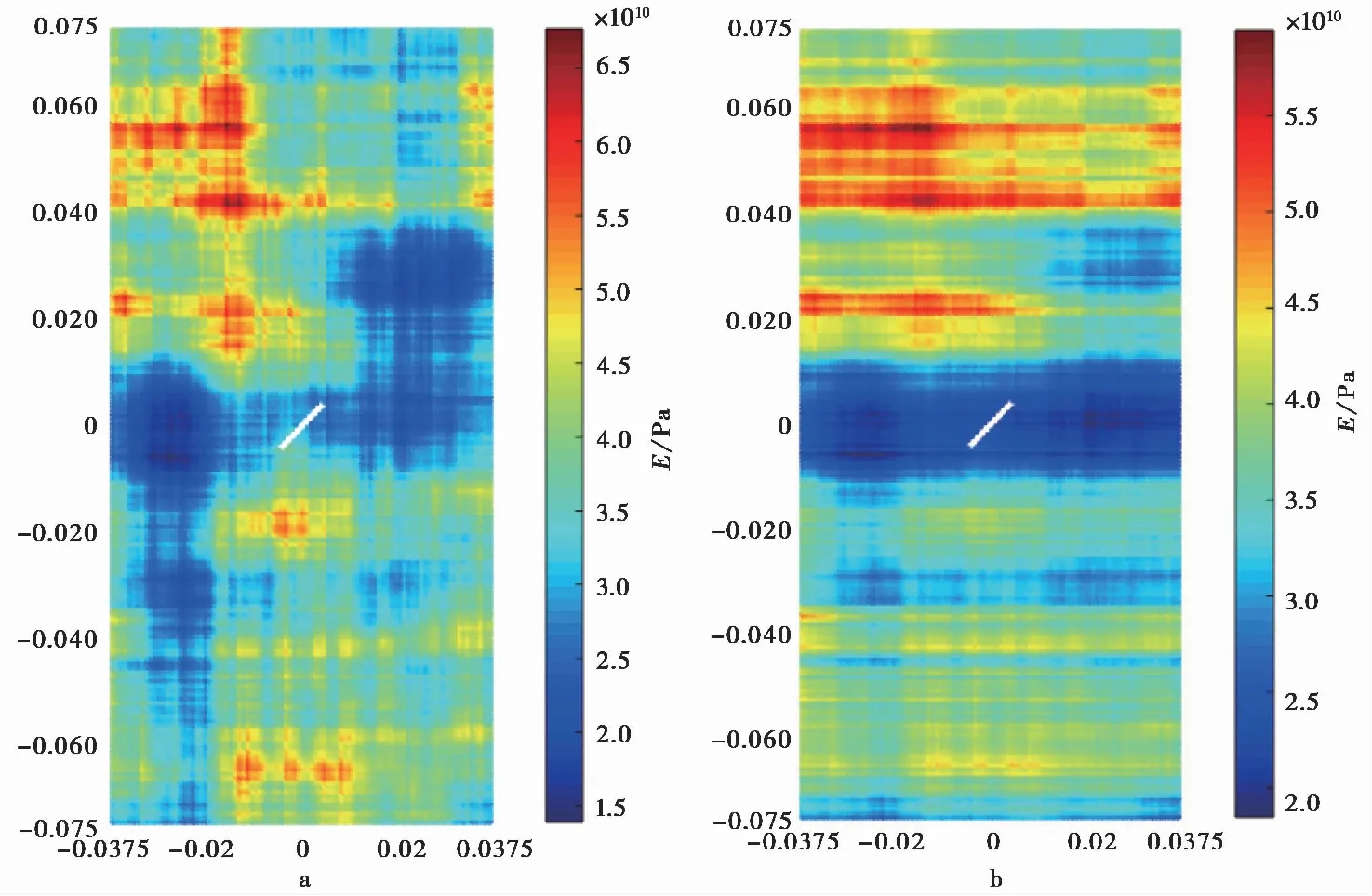
图4 不同水平波动范围下E的随机场分布

1.4 计算流程

考虑空间变异性存在时岩体损伤情况计算流程如下，做出程序计算流程图如图5所示：

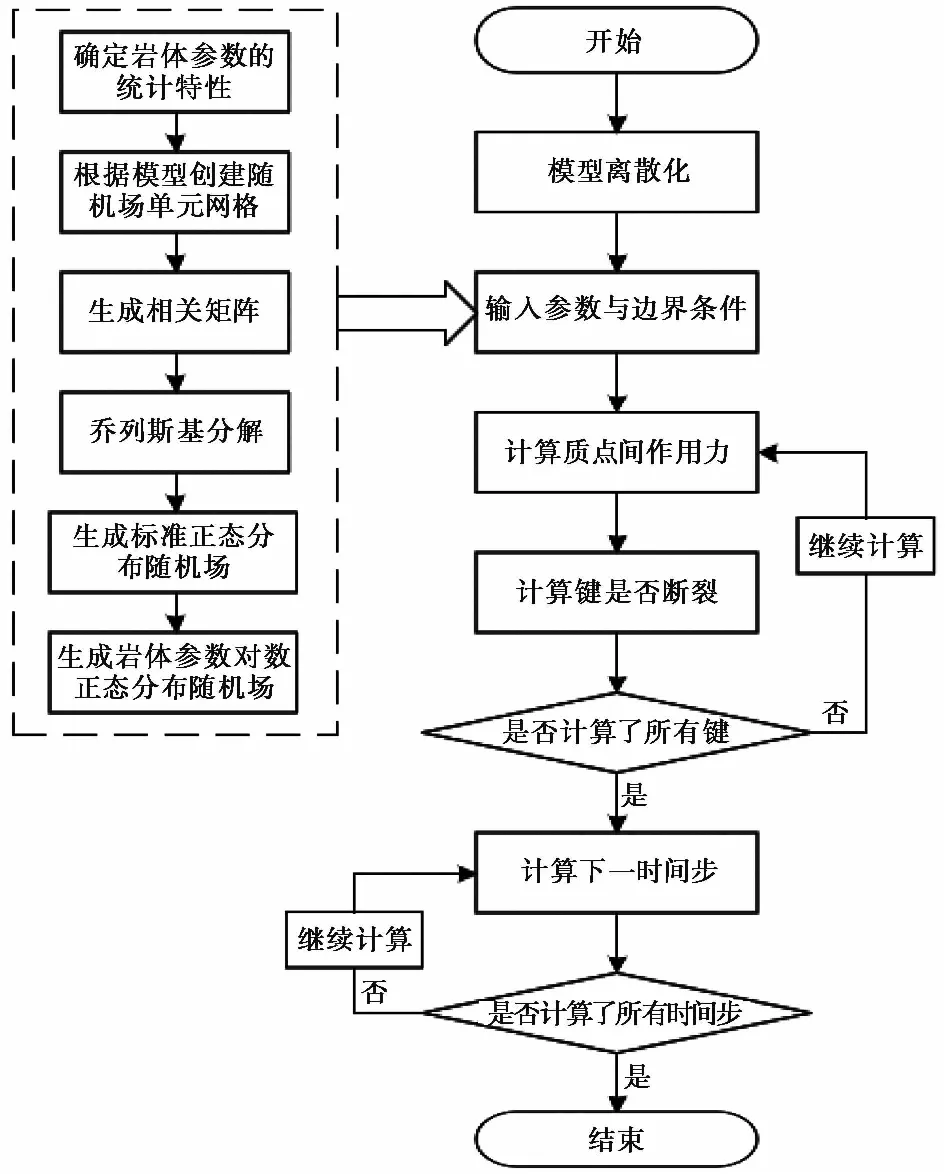
图5 程序计算流程图

(1)确定物质点间距dx与近场范围δ，模型离散化处理，确定岩体参数统计特性；

(2)根据离散化模型，创建随机场单元网格；

(3)生成不同统计参数下的岩体参数的对数正态分布随机场；

(4)将生成的随机场作为部分输入参数导入PD计算程序，确定边界条件；

(5)计算粒子间作用力，判断键是否断裂；

(6)计算每时步的所有粒子间作用力，计算所有时步，得出结果。

2 结果讨论

2.1 预制裂缝倾角的影响

为了比较不同预制裂缝倾角下后续裂纹的发展情况，选择预制裂缝倾角为30°， 45°， 60°时，分别对考虑随机场存在与不存在的情况进行了模拟，随机场参数如表1所示。不同角度下均质岩体裂纹发展图像如图6所示，考虑空间变异性时裂纹发展图像如图7所示。选择预制裂缝尖端一侧相邻3行3列共9个物质点，监测各物质点在各时步下的位移，做出9个物质点的位移均值与时步关系曲线如图8所示，通过位移时程曲线的比较说明不同情况下的裂纹发展速度。结合图6与图7对比发现考虑空间变异性时两侧裂纹发展不再完全对称且模型整体破坏更为严重。图8则表明不管是否考虑岩体的空间变异性，都是预制裂缝倾角为45°时后续裂纹发展略大于预制裂缝倾角为60°时，当预制裂缝为30°时后续裂纹发展则相对较慢。当然上述裂纹发展模拟结果除了与岩体参数有关，也会受端部约束等设置因素的影响。并且通过对比可以发现空间变异性的存在会减弱预制裂缝倾角的影响，空间变异性存在时不同预制裂缝角度下监测点最终位移差比不考虑空间变异性时更小。图8结果也表明，不管预制裂缝角度如何变化，考虑空间变异性的存在时后续裂纹的发展都更快，说明若把岩体当做均质材料时将低估岩体的受损伤程度。

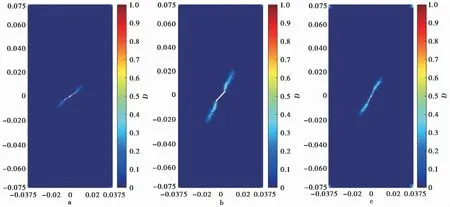
图6 均质下不同角度预制裂缝模型裂纹发展

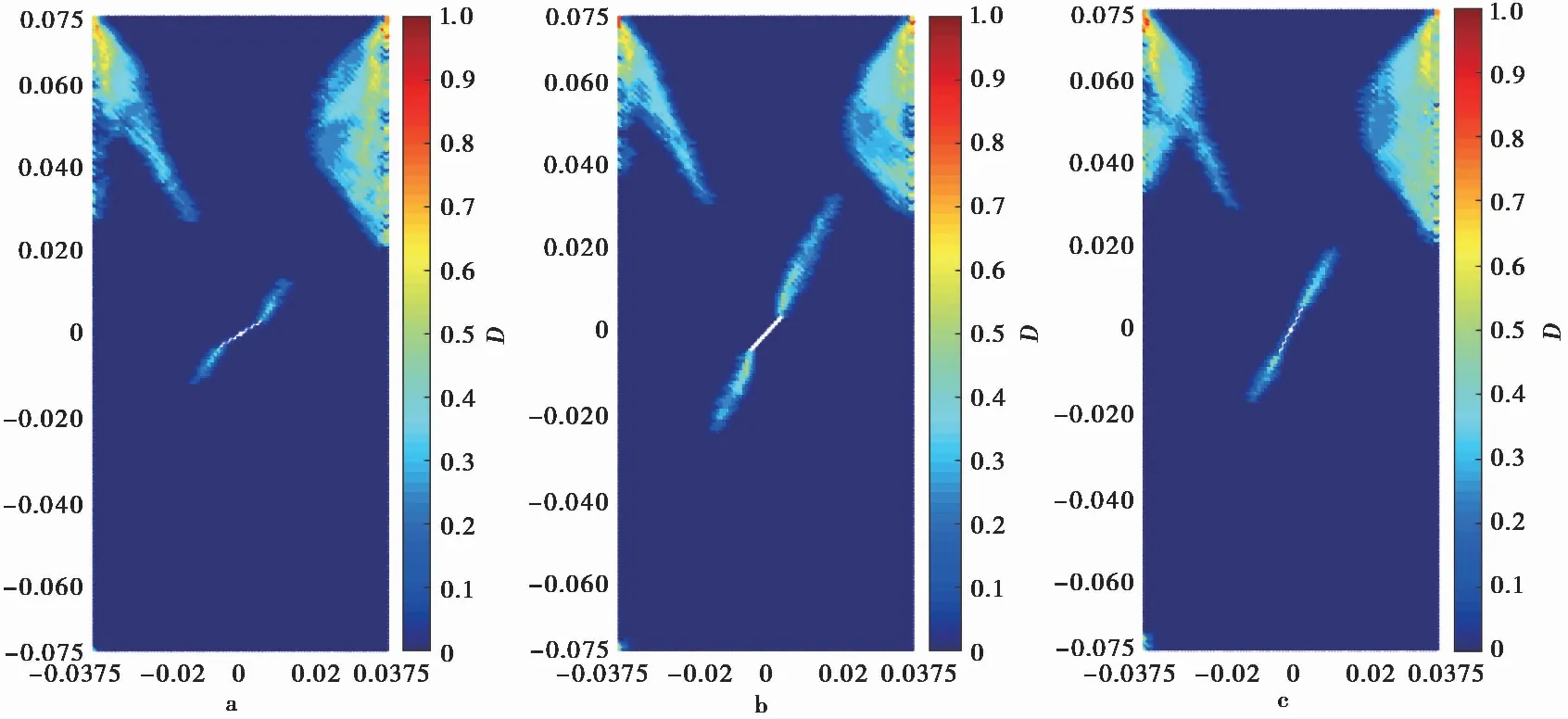
图7 空间变异性下不同角度预制裂缝模型裂纹发展

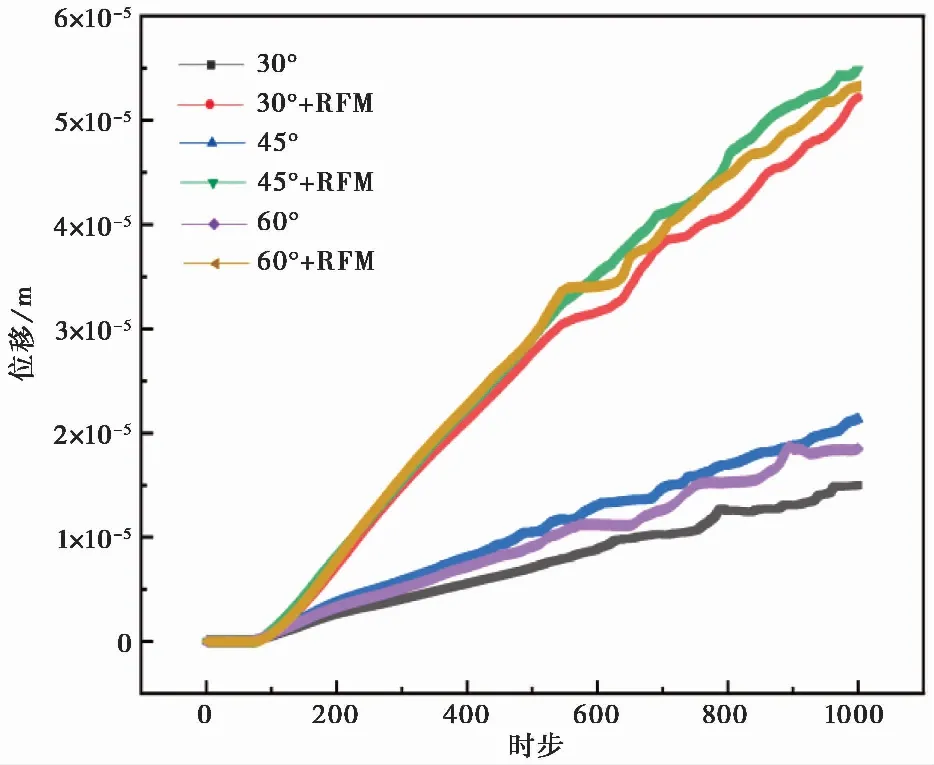
图8 预制裂缝倾角对裂纹发展的影响

2.2 变异系数的影响

为了考虑E和G0的变异程度对后续裂纹发展的影响，在随机场模型中将E和G0的变异系数COV分别设置为0.1， 0.2， 0.3， 0.4， 0.5，水平波动范围δh和竖向波动范围δv分别取0.20m和0.10m，预制裂缝倾角选择45°，预制裂缝尖端附近物质点的位移时程曲线如图9所示。结果表明E和G0的变异系数对后续裂纹的发展速率有显著影响，变异系数越高，预制裂缝尖端附近物质点位移越大，即后续裂纹发展更快。因为随着变异系数的增大，参数变异性增强，同时岩体更多部分会表现出参数E和G0数值较小的情况，因此随着变异系数的增大，裂纹发展速度明显提高。由图9可知1000时步时COV为0.5时比COV为0.1时物质点位移增长了92.796%。

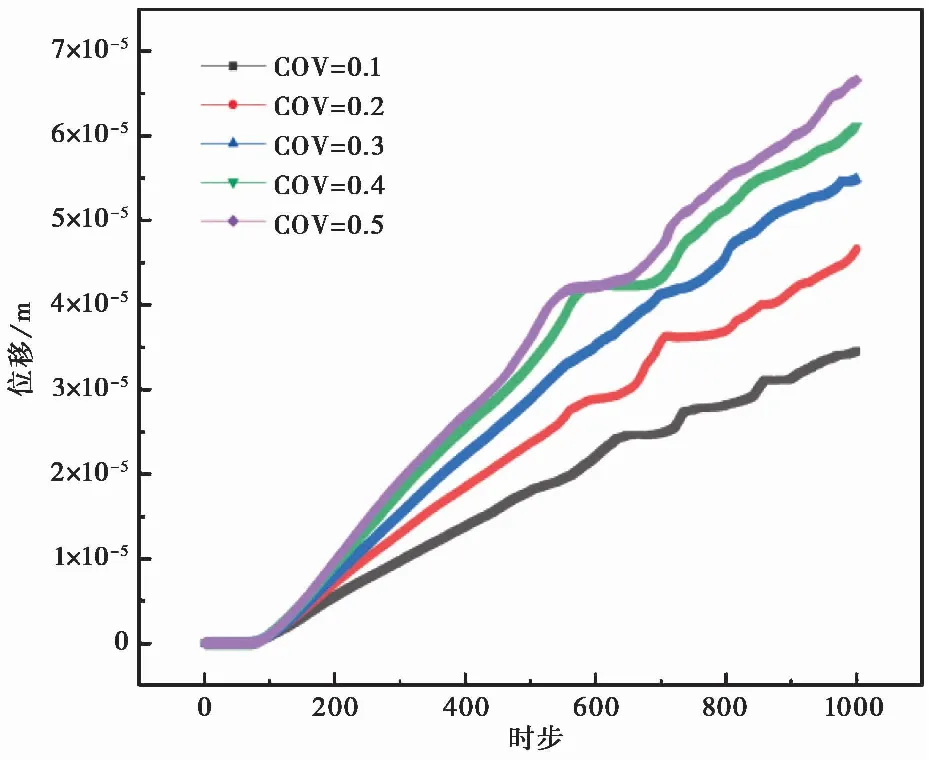
图9 变异系数对裂纹发展的影响

2.3 水平波动范围的影响

图10所示为随机场水平波动范围δh对后续裂纹发展的影响。Ching et al.(2013)研究表明，对于指数型自相关函数，随机场单元尺寸小于0.018～0.054倍的波动范围时模拟效果较好。考虑到随机场单元及模型整体尺寸，水平波动范围δh分别选择0.10m， 0.15m， 0.20m， 0.60m， 1.00m进行模拟，E和G0的变异系数取0.3，竖向波动范围δv取0.10m，预制裂缝倾角为45°，物质点位移时程曲线结果表明：整体来看，随着水平波动范围δh的增大，后续裂纹发展更快，原因归结为当δv一定时，δh越大，越接近为软硬交互的水平层状岩体，层理弱面相对而言刚度小、变形大，加载方向与层理弱面垂直，此时层理弱面对轴向压缩变形影响较大，因此随着δh的增大裂纹发展更快，这与邓华锋等(2020)的研究结果是一致的。但是δh从0.10m增长到0.20m的影响要大于从0.20m增长到1.00m的影响，原因则可能是囿于模型尺寸的限制，δh较大时对随机场模型影响已不明显。

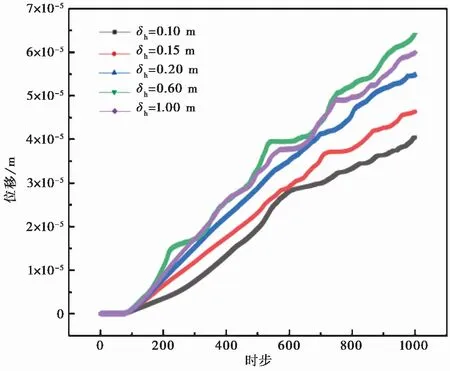
图10 水平波动范围对裂纹发展的影响

2.4 竖向波动范围的影响

图11所示为随机场竖向波动范围δv对后续裂纹发展的影响。同样基于随机场单元及模型整体尺寸的考虑，竖向波动范围δv分别选取0.05m， 0.08m， 0.10m， 0.3m， 0.5m，E和G0的变异系数为0.3，水平波动范围δh取0.2m，在预制裂缝倾角为45°模型中，位移时程曲线结果表明：整体来看随着δv的增大后续裂纹发展稍快，但是在不同δv下物质点位移区别并不大，δv对后续裂纹发展影响有限。原因一方面是模型尺寸的影响，另一方面则是δh一定时，δv越大越接近为垂直层理岩体，加载方向与层理弱面平行，层理弱面分布对轴向变形影响较小，因此表现为在不同δv下，裂纹发展速度区别不大。

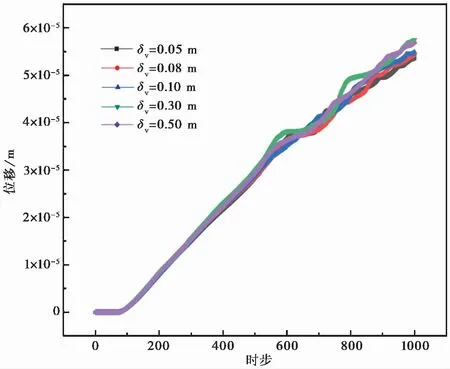
图11 竖向波动范围对裂纹发展的影响

3 结 论

本文采用了一种新的随机近场动力学方法(RPD)模拟研究了单轴压缩下含缺陷岩体的损伤情况。用近场动力学方法(PD)模拟岩体材料受压损伤过程中裂纹发展过程，用随机场方法(RFM)表征岩体材料弹性模量E和能量释放率G0的空间变异性，并利用已有模型验证了计算程序的准确性，得出主要结论如下：

(1)近场动力学方法可以有效模拟岩体材料损伤及裂纹发展问题，当考虑岩体材料弹性模量E和能量释放率G0的空间变异性时，裂纹发展速度明显加快。

(2)预制裂缝倾角对岩体损伤有较大影响，在任何预制裂缝角度下考虑空间变异性存在时，后续裂纹发展都更迅速，并且当预制裂缝为45°时，岩体最容易受压破坏。

(3)随机场参数中，E和G0的变异系数和水平波动范围δh都对裂纹发展速度有明显影响。随着变异系数的增大，水平波动范围的增大，后续裂纹发展速度都有明显提高，而在不同竖向波动范围δv下，裂纹发展速度没有太大区别。因此确定合理的随机场参数值特别是变异系数及水平波动范围，对确定单轴压缩下岩体强度及损伤至关重要。