海上风电窄深式三筒导管架偏心承载特性分析
2021-07-19杨德胡雪扬
杨德 胡雪扬
(1 福州海峡发电有限公司 福建福州 350207 2 福建省水利水电勘测设计研究院 福建福州 350001)
0 引言
随着能源结构的调整,清洁能源所占的比重逐年增长。而在清洁能源中,风能以其含量大、分布广、无污染等优势,具有广阔的发展前景。相比于陆上风能,海上风能密度更大、稳定性更高、且受地形的影响更小。因此,近年来海上风电十分迅猛,由近岸地区逐渐向深海发展[1-2]。
海上风电基础结构形式多样,对于30 m 水深以上的海域,多筒导管架结构具有很强的适用性[3-4]。海上风电基础的特点是高耸的上部结构承受的水平荷载较大,底部基础既要承受弯矩荷载也要承受水平荷载,而传统多筒导管架基础主腿底部往往位于筒顶盖的形心处,通过腹板及肋板等附属构件构成的加强段与筒体相连,而对其偏心情况下的承载力变化情况还不清楚[5-8]。本文在筒间距及筒基尺寸固定不变的前提下,针对窄深式三筒导管架基础,考虑了5 种不同主腿—筒体相对位置,调整了相应的加强段结构,分析了偏心对窄深式三筒导管架水平承载力、土压力分布规律以及旋转中心位置的影响。
1 有限元模型
为比较不同主腿位置对三筒导管架基础承载性能的影响,本节共建立5 个有限元模型,其中基础A1、A2、A、A3、A4主腿间距分别为31 m、32.5 m、34 m、35.5 m、37 m,筒高均为20 m,筒直径均为10 m,筒间距均为34 m。基础顶法兰盘距筒顶盖高度均为65.6 m,基于福建长乐海域应用的三筒结构如图1(a)所示,图1(b)为基础A 和基础A1 的有限元模型示意图。三筒导管架基础为钢结构,导管架通过加强段与筒基相连,筒顶加强段模型见图2,主要由中心筒以及8 块T 型肋板组成,两者通过顶部的钻石顶板连接固定。在ABAQUS 中采用壳单元对结构进行建模。定义材料为理想弹塑性模型,弹性模量E=206 GPa,泊松比v=0.3,屈服强度fy=345 MPa。
土体参数采用Mohr-Colunm 模型,参考某海域砂土,饱和容重为19 kN/m3,弹性模量为30 MPa,内摩擦角为30°,粘聚力为2.6 kPa。为消除边界效应对计算结果造成的影响,模型中土体长与宽均为170 m,高85 m,土体底面为固定约束,侧面采用水平约束[9]。土体采用C3D8RD 单元,网格如图3 所示。

图3 土体网格示意图
2 偏心对水平承载力及旋转中心分析
在对筒型基础的承载特性进行研究时,位移控制法与荷载控制法是两种常见的荷载施加方法。相对于荷载控制法,位移控制法能够更直观地找出基础的荷载极值,因此本文选用位移加载方法,在基础顶部法兰盘位置施加一固定大小及方向的位移,对基础的承载特性进行研究[10]。
基础A1、A2、A、A3、A4的水平荷载—位移曲线如图4 所示。各曲线荷载与位移在加载初期基本呈线性关系,随着水平位移的增加,曲线出现了“拐点”,曲线的斜率逐渐变缓,说明基础土体发生了塑性变形,较小荷载也能够使基础产生较大位移。目前通过有限元计算得到的荷载-位移曲线有陡变型和缓变型2 种情况。前者曲线存在明显的拐点,可将该拐点对应的荷载作为极限承载力,而后者曲线并没有明显拐点,可采用“双切线法”确定地基极限承载力[11]。
图4 中基础A1、A2、A、A3的荷载—位移曲线为陡变型,基础A4 的荷载位移曲线为缓变型,按照相应方法找出各基础对应的水平极限承载力分别为16.35 MN、17.90 MN、19.35 MN、21.78 MN、22.65 MN,可见在筒间距及筒径固定的前提下,主腿位置对基础的水平承载力有着显著影响,在筒顶圆心与多筒导管架基础形心的连线上,主腿底部距离基础形心越远,基础的水平极限承载力值越大。由图5 可知,各基础的水平承载力随主腿间距的增大几乎线性增加。

图4 不同主腿位置三筒导管架基础水平荷载-位移曲线(S/D=0.5)

图5 各基础水平极限承载力
图6 为水平加载过程中三筒导管架基础的旋转中心,其中绿色散点为空间点在XZ 轴上的投影。基础旋转中心的计算示意图见图7,具体计算公式如式(1)~(2):
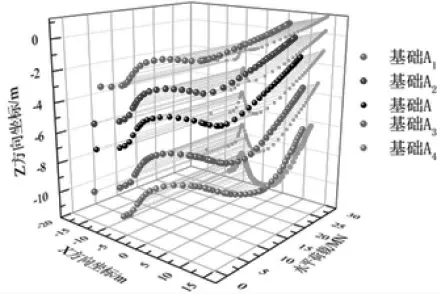
图6 水平加载过程各基础旋转中心

图7 旋转中心计算简图

式中:X0是指旋转中心到基础形心的距离(负号表示背离加载方向);Z0是指旋转中心距离泥面的距离(泥面以下为负值);Z1与Z2分别为上拔筒与下压筒的竖向位移;X1为参考点水平位移;X2为1# 筒水平位移;h0为参考点距筒顶的竖向距离;Lu为上拔筒距基础形心沿X 方向的距离;Ld为下压筒距基础形心沿X 方向的距离。
由图6 易知三筒导管架基础在水平受荷过程中,其旋转中心在水平方向上由背离加载方向一侧逐渐向受压筒处移动;而在竖向旋转中心位置呈现先接近泥面、后远离泥面、最后再接近泥面的特点,在极限承载状态时基础A 旋转中心的坐标为(-2.8 m,-6.3 m),该点即为加载过程中基础A 旋转中心位置变化的拐点。在此之前,随着水平荷载的增大旋转中心的位置在Z 方向上逐渐远离泥面,在此之后随着水平荷载的增大旋转中心的位置在Z 方向上逐渐又逐渐靠近泥面。
各基础在水平加载过程中旋转中心的变化趋势是一致的,在水平方向上由背载侧逐渐向临载侧筒基移动,在竖向先接近泥面后远离泥面,在荷载大于极限承载力之后旋转中心又向泥面处移动,基础A1、A2、A、A3、A4在极限承载状态下的旋转中心见表1,可见极限荷载下基础的旋转中心坐标在X 方向始终位于基础中轴线附近,而在Z 方向随着主腿间距的增大旋转中心逐渐向筒端移动,且各基础的旋转中心始终处于泥面以下。

表1 水平极限承载状态下旋转中心
3 偏心对土压力的影响分析
三筒基础编号及P1、P2 位置如图8 所示,2# 筒临载侧筒壁土压力沿深度方向分布如图9(b)所示,不难看出随深度不断增加筒壁所受土压力值也不断增大。对比各条曲线可知,深度在-17.5 m 以内各基础筒壁土压力值相差较小;深度超过-17.5 m 时土压力差异逐渐明显,并在筒端部达到最大值,该位置处基础A1、A2、A、A3、A4土压力分别为100.02 kPa、125.16 kPa、157.11 kPa、203.83 kPa、191.18 kPa。不难看出随着主腿间距的不断增大,上拔筒临载侧筒端土压力也随之增大。对比图9(b)与图9(d),发现1# 筒与2# 筒临载侧土压力沿深度方向的分布形式一致,但1# 筒在数值上明显大于2# 筒;观察图9(a)发现各基础上拔筒背载侧土体沿深度方向分布为波浪性,在埋深为3L/4 处土压力达到最大值,且最值同样随着主腿间距的增大而增大。

图8 三筒基础编号示意图
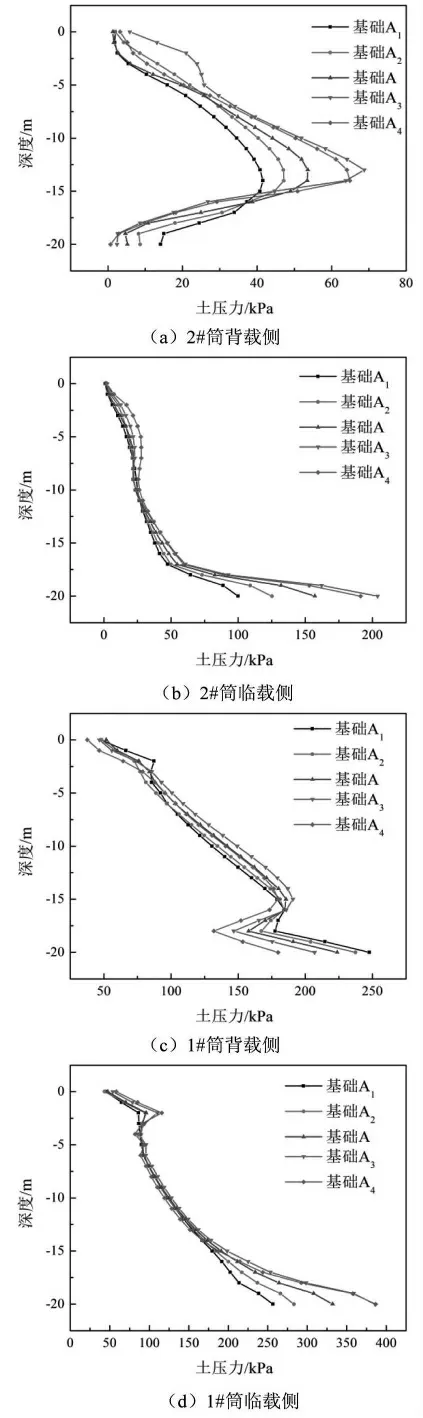
图9 不同位置筒内壁土压力沿深度方向分布
不同位置筒外壁土压力沿深度方向分布如图10 所示。结合图9,各筒壁外侧土压力沿深度方向分布与筒内土压力分布规律刚好相反:背载侧各筒土压力随埋深深度增加不断变大,而临载侧筒壁土压力沿深度呈现波浪型变化趋势,且峰值出现在埋深约为-7.5 m 的位置。通过对比分析可知,在基础埋深较浅处土抗力主要来源于筒壁沿加载方向一侧土体,而在基础埋深较深处土抗力主要来源于筒壁背离加载方向一侧土体。由图10(a)及图10(c)可知各基础2# 筒外背载侧土压力沿深度分布的差异主要体现在筒端部的位置,主腿间距越大,筒端部土压力值相应也越大;而由图10(b)及图10(d)可知筒外临载侧土压力峰值同样随主腿间距的增大而变大。

图10 不同位置筒外壁土压力沿深度方向分布
不同埋深各基础1# 筒内土压力沿环向分布如图11 所示。从图中可以看出1# 筒内外各深度土压力沿深度方向均为沿X 轴对称分布。在埋深10 m 处,1# 筒内土压力沿环向分布随主腿位置变化的差异主要体现在背载侧,主腿间距越大背载侧土压力值随之增大;而在埋深19 m 处,1# 筒内背载侧(图中角度90°到270°范围内)土压力值随主腿位置逐渐向X 轴正向移动而减小,而临载侧与之刚好相反。图12为1# 筒外不同深度土压力沿环向分布图,可知在埋深较浅处主腿间距的变化对土压力影响不大,埋深10 m 处临载侧土压力值较大而在埋深为19 m 处背载侧半边土压力值较大。

图11 不同埋深各基础1# 筒内土压力沿环向分布
图13 与图14 为2# 筒内外不同深度处土压力沿环向分布,可见2# 筒土压力并非沿X 轴对称分布,其对称轴约为165°~345°连线,从图中还能够看出筒内外土压力沿环向分布的最值也出现在对称轴处,同样地,主腿间距越大,在各位置处土压力的最值也随之增大。

图13 不同埋深各基础2# 筒内土压力沿环向分布
4 结论
本文基于海上风电三筒导管架基础,采用有限元软件ABAQUS进行数值模拟,考虑了导管架主腿与筒形基础间偏心对水平承载力的影响,结果表明:
(1)不同主腿位置对三筒导管架基础水平承载力有显著影响。随主腿位置远离基础中轴线基础的水平承载力呈线性增长,在今后的结构设计中可以结合施工工艺难度对基础筒基与导管架的相对位置进行优化,最大限度地发挥筒型基础的承载性能。
(2)水平荷载作用下,基础发生平动与转动,但以转动为主,基础的旋转中心随在水平向随水平荷载的增大逐渐由背载侧向临载侧筒体移动,随着主腿位置不断远离基础中轴线,基础旋转中心在竖向逐渐向筒端部移动。
(3)随着主腿间距的不断增大,上拔筒临载侧筒端土压力也随之增大。各基础上拔筒背载侧土体沿深度方向分布为波浪性,在埋深为3L/4 处土压力达到最大值,且最值同样随着主腿间距的增大而增大。筒内外土压力沿环向分布的极值也出现在对称轴处,同样地,主腿间距越大,在各位置处土压力的极值也随之增大。
