基于组合赋权法的建筑结构安全评价
2021-07-19蓝智川覃天乔
江 杰,汤 娟,甘 雨,蓝智川,覃天乔
(1.广西大学土木建筑工程学院, 南宁 530004;2.广西大学工程防灾与结构安全教育部重点试验室, 南宁 530004;3.广西大学防灾减灾与工程安全重点试验室, 南宁 530004;4.广西南宁市住房和城乡建设局房屋安全鉴定所,南宁 530004)
房屋的安全性关系到人民群众的生命财产安全和社会的长远发展,是目前政府部门高度重视的民生问题之一[1]。近年来,越来越多的安全问题在既有建筑物使用过程中逐渐显露出来,例如建筑物使用功能以及周围环境的改变,致使建筑物结构性能逐渐降低乃至丧失。因此,采取合理的科学方法对房屋安全现状进行评估,及时发现潜在的不安全因素,采取正确的措施对建筑物进行维修加固,不仅可以延长房屋的使用寿命,更重要的是避免房屋事故的发生,还能提高房屋的使用安全性。
目前,其他领域的风险评估方法相对成熟,但关于建筑物结构进行安全评价方面的研究较少。赵挺生等[2]基于高速公路施工临近房屋安全风险评估模型提出熵权法和控制区间与记忆模型对公路施工引起临近建筑物风险进行评价。郭小东等[3]首先运用层次分析对木结构古建筑进行各指标因素的权重,在采用灰色白化权函数聚类法进行聚类分析,按灰色聚类系数最大值原则对木结构古建筑进行安全性评价。秦本东等[4]采用层次分析法与模糊数学相结合的方法对古建筑的安全状态进行评估。田宇等[5]基于系统科学的层次分析法,对各因素进行指标权重的计算,建立装配式住宅建筑的安全评价体系,并用实例论进行论证。王思莹[6]利用层次分析法确定各级评价指标的权重,再通过物元可拓模型对砖木结构古建筑进行综合评价。由上述文献可知,目前主要采用层次分析法对房屋建筑安全性进行评价,这种评价方法主要依赖于专家工程经验,缺乏理论依据并且存在较大的主观性,而各因素指标间的不确定性以及差异性还需进一步探讨。
鉴于此,基于多层次房屋安全评估模型提出主客观耦合赋权法的模糊综合评价方法及《危险房屋鉴定标准》(JGJ 125—2016)[7],现以房屋安全状况的初步调查和房屋日常安全检查、检测结果为依据,总结出破坏房屋结构构件的主要影响因素,建立房屋安全性评价体系,采用最小离差法计算指标的组合赋权值,并选取岭型分布函数计算评价指标的隶属度,通过定性、定量相结合的方式对房屋的状态进行安全评估,并通过工程实例来验证其准确性。
1 建立房屋建筑安全评价体系
采用多层次指标来建立房屋建筑安全评价体系。在建立合适的房屋安全评价体系过程中,可以使用现有的规范和标准,为了提高房屋安全评价的准确性,建立的评价指标都需要反映房屋建筑某一部分的安全性能。针对房屋建筑破坏的特点,将影响房屋建筑的安全因素划分为六大类:地基基础、承重梁、承重柱、墙体、楼板层和围护系统,在影响自身性能的六大类安全因素的基础上建立更加全面的分项评价指标。所建立的房屋建筑安全性评价指标体系如图1所示。

图1 房屋建筑安全性评价指标体系
2 建立多层次模糊综合评价模型
2.1 建立房屋安全建筑评价模糊集合
房屋建筑安全性评价模糊集合是由房屋安全的关键因素来确定,将房屋安全状态划分为安全v1、较安全v2、较危险v3和危险v44个状态,V={Vk}={v1、v2、v3、v4},所对应的房屋安全等级分布为A级、B级、C级和D级。
2.2 权重确定
目前来说,主观赋权和客观赋权是确定指标权重的两大类常见方法:其中专家经验是决定各项指标优先程度的主观赋权法,该方法太过依赖专家的实际经验进行主观臆断;根据收集客观信息计算得出各项指标重要程度的客观赋权法,虽然克服人为因素的影响,但赋权结果往往和实际存在一定偏差。因此,采用区间层次分析法与熵权法相结合的方式代替层次分析法确定指标的基础权重,再利用最小离差法确定指标的综合权重,从而提高了评判结果的精度,使评价结果更贴合实际情况。
2.2.1 区间层次分析法求权重
区间层次分析法(interval analytic hierarchy process,IAHP)[8]是将区间算法和传统层次分析法相融合的分析算法,它以区间数替代点值来构成判断矩阵,解决同层指标在相互比较时出现的不确定问题,采用区间层次分析法更符合实际情况。采用该方法计算主观权重主要步骤如下。


表1 1~9标度法判断标准

w1=αw-,w2=βw+
(1)
(2)
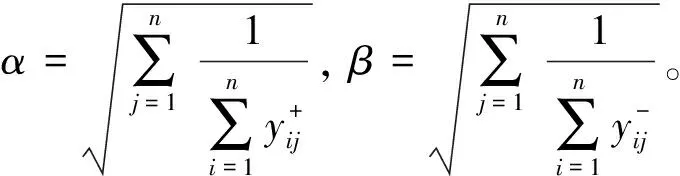
(3)计算主观区间最终权重wj′。
(3)
(4)一致性检验。
(4)
2.2.2 熵权法求权重
熵权法(the entropy weight method,EWM)[12]是根据指标差异程度来计算各项指标所占基础权重的客观赋权方法,一般而言,若某个指标的熵值越小,在综合评价中起的作用越大,其权重也就越高。熵权重计算步骤如下。
(1)构建原始数据矩阵。数据包括m个样本,n个指标,形成原始数据矩阵X=(xij)nm,i=1,2,…,n;j=1,2,…,m。
(2)归一化矩阵。为了消除各指标间量纲上的差异,对原始数据进行无量纲处理,各指标间贴近度用规范化后的指标值来确定,并得到各指标归一化矩阵P=(pij)为
(5)
(3)计算信息熵和差异系数。
(6)
式(6)中:k=1/lnm,信息熵ej=1时,这项指标的权重为零,对整体评估无影响;当同一指标的hj越大,ej就越小[13],权重就越大,说明该项指标对整体评估有着重要影响。
(4)计算熵权w″j。
(7)
2.2.3 组合赋权
综合权重是采用最小离差法对前文获得的主、客观基础权重进行耦合优化。令α和β分别表示w′和w″的所占综合权重的重要程度,即
wj=αwj′+βwj″
(8)
设α2+β2=1,构造目标模型为
(9)
利用Lagrange条件极值原理,分别计算出主、客观基础权重在综合权重中所占比例,并计算每个指标对应的权重值,公式为
(10)
wj=α*wj′+β*wj″
(11)
为了阐明IAHP-EWM的综合权重的计算过程,以地基基础的综合权重计算过程为例。
0.96;
1.03;
同理,根据以上公式计算得到其他评价指标的综合权重,计算结果如表2所示。
利用IAHP与EWM耦合优化的方式,得到各评价指标综合权重,从表2结果看出,地基基础在评价指标中占的比重较大,承重柱的影响作用大于承重梁,影响作用最小的是围护系统,从建筑结构设计角度出发,所得因素集综合权重符合构造原则。

表2 EWM-IAHP指标权重
2.3 建立房屋建筑安全评价指标评判标准
根据影响因素的特征分别建立定量和定性两种评价指标的标准。利用定量的方法对墙体稳定性、变形、构件承载力等进行评价;利用定性的方法对构件的连接、损坏以及墙体的隔音防火等性能进行评价。建立构件表观类和承载力评判标准[14]如表3所示,其余评判标准均借鉴相关规范建立。

表3 承载力及表观类评定指标标准
2.4 建立合适的隶属函数
考虑到评价指标的特点,采用岭型分布函数[15]。建立隶属函数进行定量评价时考虑到两种类型的岭型分布函数如图2所示。图2(a)是适用于承载力这类“越大越有利”型的隶属函数,图2(b)是适用于变形、裂缝等外观类“越小越有利”型的隶属函数。

图2 两类隶属函数
2.4.1 “越大越有利”型评价指标的隶属函数
承载能力越大,建筑结构构件的安全性就越高,这类评价指标应选用“越大越有利”型建立隶属函数。以地基等构件的承载力为例,建立四等级岭型隶属函数评判标准为
(12)
(13)
(14)
(15)
2.4.2 “越大越有利”型评价指标的隶属函数
影响房屋建筑表观的安全因素,其构件的裂缝宽度和变形量越小,结构性能就越高,应选用“越小越有利”型建立隶属函数。以混凝土柱弯曲变形评价指标,建立四等级岭型隶属函数评判标准为
(16)
(17)
(18)
(19)
从房屋建筑安全角度出发,在建立四等级岭型隶属函数过程中,应将房屋其他安全等级区间划分得比较危险状态区间范围稍小一些。从概率学角度来讲,让房屋建筑出现较危险状态的概率比其他安全等级的概率稍大一些,使房屋建筑的安全具有足够储备能力。
2.5 建立因素集对应的评价矩阵
根据各个因素的特点,选用合适的隶属函数,根据所建立的评判因素集ui和与之对应的评价集V,建立模糊评价的单因素评价矩阵。
(20)
式(20)中:Ri为单因素评判矩阵;rijk为第i个因素中第j个子集因素uij在评价集V上对应的等级k的隶属度。
2.6 模糊综合评价
按照模糊综合评价中权重集与单因素评价矩阵的合成法则,从底层评价指标逐步向上进行合成,逐步完成整个目标的模糊综合评价,具体步骤按照式(21)和式(22)进行计算。
Bi=Wi∘Ri=[Bi1Bi2…Bij]
(21)
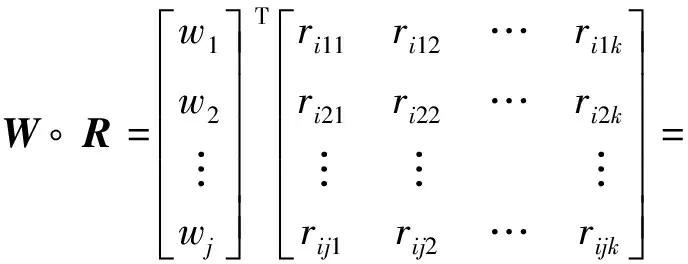
(b1,b2,…,bk)
(22)
式中:B为评价集上的等级模糊子集;“∘”为模糊算子采用加权平均型求解模型,计算模型考虑了每个评价指标对房屋建筑影响的情况,并按照模糊识别原理,从综合评价结果向量B中选择最大隶属度的bi所对应的房屋安全等级vi作为最终的评价结果,使得最终的评价结果更加真实和准确。
3 工程算例
3.1 工程概况
该楼房位于南宁市兴宁区望州路南二里86号,建于1996年,功能为住宅楼,为五层砖混结构,其中一层3.3 m,其余层3.0 m,建筑总高度为15.3 m。该楼总建筑面积为244.8 m2,按7度地震烈度设防,建筑耐火等级为二级。
3.2 评价矩阵的确定
(1)地基基础。通过现场查勘,该住宅楼所建位置较为平坦,土质较软且地表不存在裂缝;该建筑基础型式为钢筋混凝土独立桩基础,地基基础完好,经检测得地基不均匀沉降量0.001 1 mm,地基的不均匀沉降并未导致上部结构发生墙体裂缝;对住宅楼检测数据进行整理,地基承载力为1.37,基础的承载力为0.99,则地基基础的评价矩阵R1为
(23)
(2)承重梁。根据现场的检测数据显示,1/5的承重梁的承载能力为1.335,4/5的承重梁的承载能力为1.29,加权平均则承重梁的承载力为1.299。少部分的梁体变形为4.995 mm,大多数的梁体变形为5.535 mm,此处按最大变形值取5.535 mm,该楼的梁端连接局部有轻微的缺陷,但不影响构件,个别梁体存在微小的裂缝,检测到梁体最大裂缝宽度为0.13 mm,则住宅楼承重梁的评价矩阵R2为
(24)
(3)承重柱。通过收集现场的检测数据可知,50%的柱体承载力为1.056,50%的柱体承载力为0.96,为了安全起见考虑取最小值0.96;70%的柱体变形为9.35 mm,30%的柱体变形为10.18 mm,此处利用加权平均法取柱体变形为9.599 mm;该楼的柱端连接方式正确,构造符合国家标准规范的要求,仅有局部的表面出现缺陷,但对构件无影响,则住宅楼承重柱的评价矩阵R3为
(25)
(4)墙体。经现场检测,外围护墙的整体性远小于A级限值,该楼的顶点侧向最大位移为3.672 mm,最大的层间位移为1.89 mm,大部分墙体无明显的裂缝损伤,少部分墙体局部表面存在缺陷,根据资料显示该住宅楼为二级耐火等级的建筑,墙体的隔音、保温、防水火功能良好,并且房屋未出现漏水火灾等现象,则住宅楼墙体的评价矩阵R4为
(26)
(6)楼板层。现场采用电镐对混凝土楼板进行局部开洞测量,经检测结果可得,板厚跨比值均大于1/30,测得楼板层构件最大变形为9.35 mm;楼板层并无明显的裂缝及损伤,并未发生火灾,则楼板层的评价矩阵R5为
(27)
(7)围护系统。经现场调查,该住宅楼每层都设有窗户,采光能力良好,楼梯基本无变形,但楼梯扶手局部有细微的破损现象;门窗强度较高,少数窗框抹灰出现局部脱落;屋盖构件整体连接正确,并且防水性能良好,围护系统的评价矩阵R6为
(28)
3.3 模糊综合评价
根据式(21)和式(22)对住宅楼安全性进行模糊综合评价,计算结果为
(29)
根据模糊综合评价的计算结果可知,其中最大评价值为0.604,按照最大隶属度原则可知,则该住宅楼的安全评价等级为B级,处于较安全的状态,但个别构件存在安全问题,需要对其采取针对性的修缮加固处理。
建立的房屋安全评估模型同专业鉴定人员根据现行标准规范对该住宅楼进行安全评价结果相比,利用所提出的评价方法更接近于实际情况。
4 结论
运用区间层次分析法、熵权法和模糊数学理论,结合现有标准和规范建立房屋建筑安全性评价体系,并利用工程实例对所建模型的可行性进行验证,得到如下结论。
(1)利用最小离差法对区间层次分析法与熵权法进行耦合赋权,确定各指标的综合权重,消除各指标间的差异性;同时引入了岭型隶属度函数,定量、定性地对建筑房屋安全状态进行综合评价,能较全面、准确地反映房屋结构各方面情况,且具有可操作性。
(2)构建了符合房屋结构损坏特点的岭型分布隶属函数,且房屋建筑较危险状态比其他状态的区间取值范围稍广,确保了房屋建筑有一定的安全储备能力。
(3)基于房屋安全评估模型提出的评价方法对南宁市某住宅楼进行安全评估,得出该住宅楼处于较安全状态,但根据各构件评价结果显示,个别部位存在安全隐患,在后期修缮过程中需要进行针对性加固措施。该工程实例得到的评价结果与鉴定人员根据现行规范所得情况一致,验证本文方法是切实可行的。
