基于特征模型的力矩受限卫星姿态抗饱和设计

郭瑞科，胡 军，李毛毛，张 涛

（北京控制工程研究所，北京 100190）

0 引言

航天器技术的发展和航天任务复杂度的提高对控制能力提出了更高的要求，然而航天器姿态控制中执行器所能输出的控制力矩存在一定限制，也就是存在饱和非线性。如果设计控制器不考虑执行器存在饱和非线性，当执行器发生饱和时，控制器的输出和被控对象的输入值不相等，可能会导致航天器姿态控制精度变差或闭环系统不稳定。通过设计抗饱和补偿器恢复闭环系统性能或者稳定性，是解决执行器饱和影响控制性能或闭环系统稳定性的一种途径［1］。

目前，航天器姿态控制抗饱和研究取得一些进展［2-8］。MARCO 等［9］提出了基于线性矩阵不等式（LMI）的线性离散系统抗饱和设计方法，给出了静态和动态抗饱和补偿器的构造算法，尤其是对于静态或者被控对象同阶的抗饱和补偿器构造条件可以转化为凸约束的LMI 条件。于海祥等［10］针对大角度姿态机动卫星存在控制输入饱和问题，在建立被控对象特征模型的基础上，设计了基于特征模型的低增益反馈控制器，使得复杂被控对象也可以用低增益的设计方法解决控制输入饱和问题。王明钊等［11］将LQG 控制方法和基于LMI 抗饱和补偿器相结合，保证了控制输入受限航天器闭环稳定，且满足最优的L2 指标。李德婷等［12］针对单框架控制力矩陀螺的力矩输出具有奇异饱和性能的特点，设计了基于平坦微分理论的快速参考轨迹规划方法和滑模控制器相结合的控制方法，避免出现奇异饱和失效现象。文献［13］考虑了一类具有状态独立的输入饱和非线性系统，提出了新的控制策略，设计的非线性控制器使得系统是局部渐近稳定的。WADA 等［14］对使用模型预测控制器的线性离散系统设计抗饱和补偿器，将抗饱和补偿器的求解转化为LMI 优化问题，保证了存在输入饱和时的系统稳定性并改善了瞬态响应。然而这些方法都只适用于定常线性离散系统，对于非线性系统或者系统参数不确定时，该方法应用受到限制。

吴宏鑫等［15］提出了根据对象动力学特性、环境特征和控制性能要求相结合来建模的特征建模思想，以期在满足性能指标的情况下设计出简单低阶控制器。一般情况下，特征模型用慢时变低阶差分方程描述，工程和应用研究中使用最广泛的是二阶差分特征模型。基于特征建模的黄金分割控制能保证参数未知定常系统在过渡阶段，参数估计未收敛情况下闭环稳定，设计简单，参数鲁棒性好。但基于特征模型的黄金分割控制器所针对的对象模型还没有考虑过执行器存在饱和的情况。当不考虑执行器饱和现象，常规设计的控制器在执行器发生饱和时将不能保证控制性能或者闭环系统的稳定性。

本文提出将黄金分割控制器和基于LMI 抗饱和设计相结合的控制方法，针对存在控制力矩饱和约束的卫星姿态跟踪控制问题，首先设计不考虑输入饱和的定常黄金分割控制器；其次用特征模型取代原被控对象求解抗饱和补偿器，将求解抗饱和补偿器的约束条件转化为凸约束的LMI 条件，设计过程保证了整个闭环系统的稳定性。数值仿真验证了所提出方法对控制力矩受限卫星姿态跟踪控制的有效性和鲁棒性。

1 问题描述

1.1 挠性卫星动力学系统描述

挠性卫星俯仰轴动力学的简化模型可以写成如下形式：

式中：J为卫星转动惯量；ω为俯仰角速度；T为控制力矩；G=[g1g2]T为挠性模态与卫星俯仰运动的耦合系数矩阵；q=[q1q2]T为模态坐标；Λ=diag(Λ1Λ2)为约束模态频率。

参考文献［10］，上述挠性卫星俯仰轴动力学模型的特征模型可以用如下形式的二阶差分方程表示：

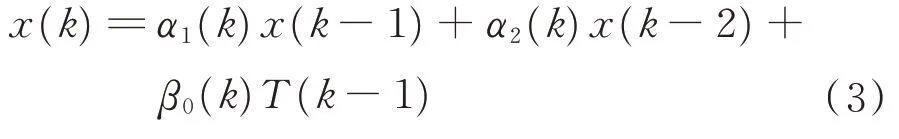
式中：α1(k)、α2(k)、β0(k) 未知，但在已知闭凸集之内［15］。

参考文献［15］中定理5.1，对式（3）中α1(k)、α2(k)、β0(k)取稳态值，得到

对式（4）设计定常黄金分割控制器，作为系统控制输入未受限时的标称控制器，可以保证闭环系统稳定并满足性能，即

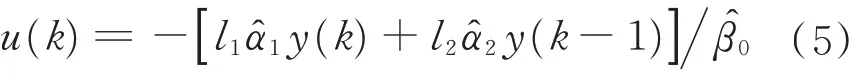
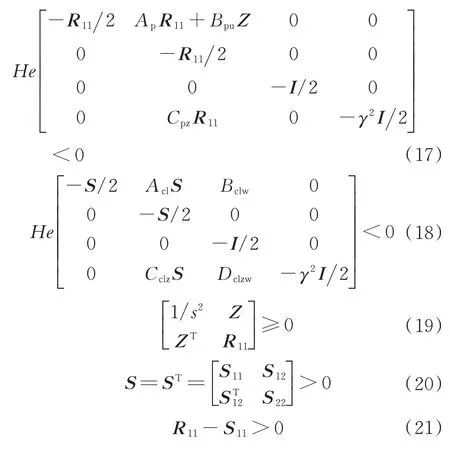
式中：l1=0.382；l2=0.618；为特征模型辨识参数，此处取稳态值。

当被控对象的控制输入存在饱和非线性时，也就是控制输入满足

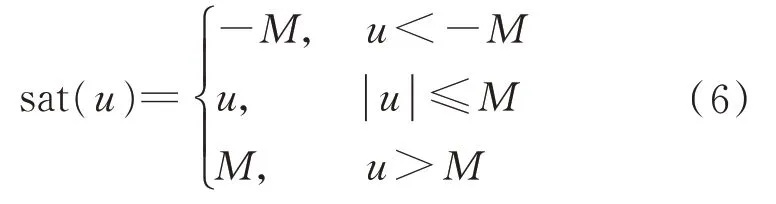
需要设计线性抗饱和补偿器，保证参考输入w和输出性能z之间l2增益满足控制要求。假设设计naw阶的抗饱和补偿器，naw≥0，定 义q=u−sat(u)，

由被控对象、黄金分割控制器、抗饱和补偿器组成的闭环系统示意图如图1 所示。

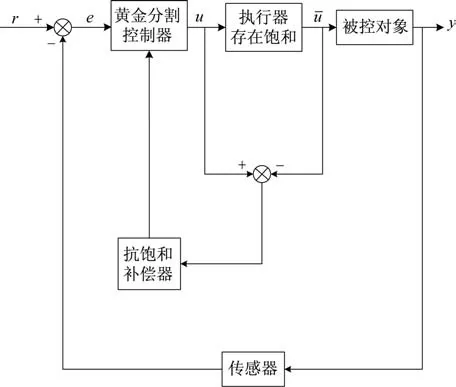
图1 抗饱和闭环系统Fig.1 Anti⁃windup closed⁃loop system

1.2 控制律变换

为了便于设计抗饱和补偿器，需要将定常黄金分割控制律写成状态空间形式。基于误差的黄金分割控制律为

若被控对象存在控制输入饱和，加入抗饱和补偿器输出的控制律为

1.3 闭环系统

为便于求解抗饱和补偿器，将式（4）写成状态空间形式，得

2 抗饱和补偿器构造

2.1 抗饱和补偿器存在性线性矩阵不等式条件

定理1给定被控对象（15）、控制器（13），当且仅当存在正定对称的矩阵R11、S，矩阵Z，正数γ，使得下述线性矩阵不等式可行时，被控对象（15）、控制器（13）组成的闭环系统在控制输入满足式（7）饱和非线性约束时，使闭环系统适定且保证局部二次型l2性能的抗饱和补偿器（7）存在［8］。

下文中对矩阵X，He(X)=X+XT，

2.2 抗饱和补偿器的构造方法

前述定理给出了与被控对象同阶的抗饱和补偿器可行性线性矩阵不等式条件。然而在抗饱和设计中，需要求解出抗饱和补偿器的系数矩阵，因而下面给出具体的构造方法［16］：

3 实验仿真

考虑文献［10］中的对象，对称挠性帆板卫星的俯仰轴动力学，采样时间Ts=0.1 s，模型参数如下：

控制输入u限制为±30，可以设计被控对象同阶的抗饱和补偿器，通过固定参考输入yr的l2增益s，求得最优γ，以实现闭环稳定和局部的性能指标。

抗饱和补偿器与被控对象同阶（naw=2），取s=0.29，可求得γ=349.06，抗饱和补偿器系数矩阵为

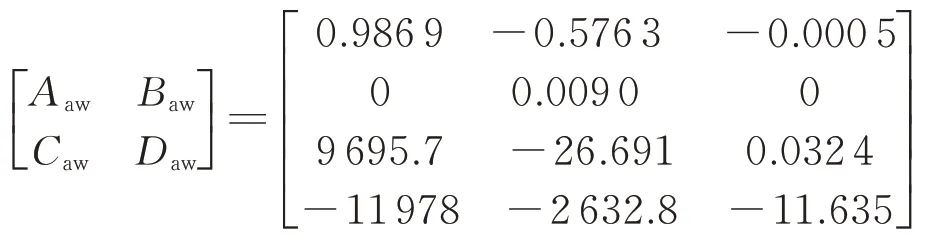
控制输入未受限时，所设计的控制律可以很好地跟踪参考输入，控制量最大值为978.9。当控制输入的幅值限值在±30 时，闭环系统受到饱和影响，可以看到控制性能明显变差，输出难以跟踪参考输入，控制输入在±30 多次振荡，如图2 和图3所示。

图2 不存在与存在输入饱和时的闭环响应Fig.2 Closed-loop responses without and with input saturation

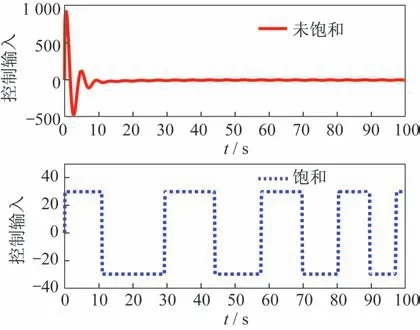
图3 不存在与存在输入饱和时的控制量Fig.3 Control inputs without and with input saturation

3.1 被控对象同阶抗饱和补偿器(naw=np=2)

根据2.2 节步骤设计的被控对象同阶抗饱和补偿器控制结果如图4 所示。图中可见，采用被控对象同阶抗饱和补偿器之后，闭环系统的输出能较好地跟踪参考输入，相比较与饱和系统控制效果有明显提升。通过图5 所示的几拍bang-bang 控制能够很快地恢复不受限的闭环响应，说明这种动态抗饱和补偿器是有效的。需要注意的是，在初始跟踪阶段，跟踪性能还是有较小的损失，这也是抗饱和补偿器在保证饱和性能同时，不可避免地损失小信号时的闭环响应性能。

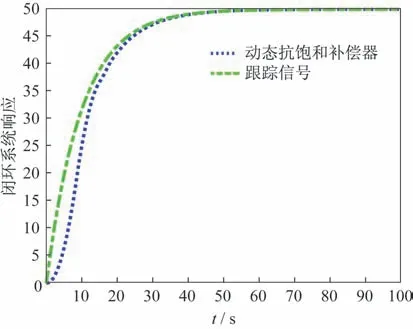
图4 采用动态抗饱和补偿器的闭环响应Fig.4 Closed-loop responses with dynamic anti-windup compensator

图5 采用动态抗饱和补偿器时的控制量Fig.5 Control input with dynamic anti-windup compensator

3.2 黄金分割控制器与低增益饱和控制器对比仿真

此处进一步对比了定常黄金分割控制律和文献［10］中所采用低增益控制律时，闭环系统响应和控制量的不同。如图6 所示，控制输入受限时，采用两种控制器的闭环系统都在瞬态响应有轻微的性能损失，但采用动态抗饱和补偿器的黄金分割控制相比低增益饱和控制器能更好地跟踪参考信号，同时采用定常黄金分割控制的控制量只有较少的振荡，变化较平滑，如图7 所示。

图6 采用动态抗饱和补偿器和低增益控制器的闭环响应Fig.6 Closed-loop responses with dynamic anti-windup compensator and low-gain controller

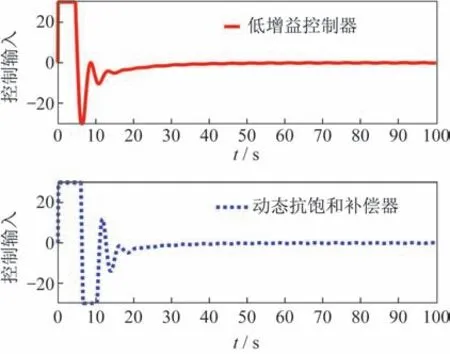
图7 采用动态抗饱和补偿器和低增益控制器的控制量Fig.7 Control input with dynamic anti-windup compensator and low-gain controller

4 结束语

本文将黄金分割控制器和基于LMI 抗饱和设计相结合，首先设计不考虑输入饱和的定常黄金分割控制器；其次用特征模型取代原被控对象来求解抗饱和补偿器，将求解抗饱和补偿器的约束条件转化为凸约束的LMI 条件。设计过程保证了整个闭环系统的稳定性，解决了存在控制力矩饱和约束的卫星姿态跟踪控制问题。数值仿真验证了所提出方法对控制力矩受限卫星姿态跟踪控制的有效性和鲁棒性。