四维黎曼时空下脉冲星导航模型精度分析
2021-07-18王龙奇马家辰
姜 宇,陈 晓,王龙奇,金 晶,马家辰
(1.哈尔滨工业大学 航天学院,黑龙江 哈尔滨 150001;2.上海卫星工程研究所,上海 201109)
0 引言
脉冲星是一种高速自转的强磁化中子星,具有自转周期稳定、辐射光子能量集中的特点。它能够为近地轨道、深空和星际空间飞行的航天器提供位置、速度、时间和姿态等导航信息,实现对长时间在轨航天器的高精度自主导航与控制,具有广阔的工程应用前景[1-2]。
脉冲星的自转轴与磁轴存在固定夹角,又因为脉冲星的自转周期非常稳定,航天器接收到周期性的光子信号。
记录航天器单位时间内接收的光子数可以获得脉冲星观测轮廓,对比脉冲星的观测轮廓和太阳系质心(Solar System Barycenter,SSB)的标准轮廓可以得到光子到达航天器与SSB 的时间差。把时间差作为观测量建立三维观测模型,结合轨道动力学模型,利用相关滤波算法可以得到航天器的位置和速度信息[3-7]。
随着空间探测向大尺度时空发展,计时精度向纳秒量级提高,三维欧式空间下的脉冲星光子传播模型已经不能满足精度要求。光子在传播过程中,不仅需要考虑其周年视差效应、多普勒频移以及等离子体的色散延缓,还要考虑太阳系引力的弯曲效应[8-10]。
文献[11]基于DSX 体系下的后牛顿近似方法,将SSB 坐标系作为航天器导航的参考系,推导了1PN、2PN 度规下的高精度观测模型,可以满足纳秒量级的时间测量精度。
文献[12-13]提出在四维光坐标框架下讨论脉冲星光子传播问题,将4 个脉冲星的固有时作为四维平直时空的光坐标,可以为太阳系内的任意观测者导航,由此建立相对论定位系统理论框架。
文献[14]在四维黎曼时空中引入相对论定位系统,建立四维观测模型,与传统的三维观测模型相比引入时间状态量,提高了时间估计的准确性,且不必推算标准轮廓的相位,减小了标准轮廓的拟合误差。
X 射线脉冲星自主导航依赖于精确的时间测量,航天器时钟记录的固有时与SSB 坐标系下的坐标时不同步,在500 s 的观测窗口下,固有时和坐标时会产生微妙量级的误差,代入迭代过程会导致滤波器发散,所以需要引入时间转换模型。利用光子运动的四维时空间隔为零,可以得到固有时与坐标时的基本关系。
文献[15-16]研究环火星探测器星载时钟在1PN 度规下的时间转换关系,通过数值分析得出时间不同步主要受太阳引力和航天器速度影响,可达亚秒/年量级。上述关系式以坐标时作为自变量进行积分运算,并且积分式中涉及航天器的位置、速度信息,很难实现从固有时到坐标时的转换。
文献[17]根据广义相对论的后牛顿近似理论,在忽略太阳系天体自转和扁率的情况下,利用能量守恒定律推导出航天器绕飞的时间转换模型,模型精度在纳秒量级。文献[18]针对航天器绕地变轨时可能做抛物线或双曲线运动推导了更加全面的时间转换模型,对文献[19]进行了补充分析。
本文基于绕飞轨道研究高精度脉冲星导航模型,为脉冲星导航的深空探测提供理论基础,所做工作集中在以下两方面:在四维黎曼时空下建立脉冲星导航系统状态模型和四维观测模型,并基于无迹卡尔曼滤波(UKF)方法设计脉冲星导航算法;对引入的四维观测模型和时间转换模型进行误差分析,研究影响导航精度的主要因素。
1 四维黎曼时空下的X 射线脉冲星导航模型
1.1 航天器轨道力学模型
选取太阳系质心天球参考系(Barycentric Celestial Reference System,BCRS)的时空度规,建立带有时间转换项的航天器轨道运动学模型。X 射线脉冲星导航原理图如图1 所示。
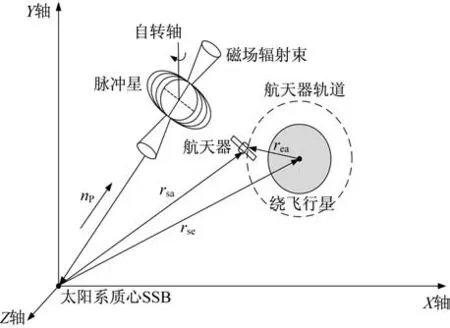
图1 X 射线脉冲星导航原理图Fig.1 Schematic diagram of X ray pulsar-based navigation
四维黎曼时空下航天器的状态x定义为

式中:t为航天器的坐标时;rsa=rse+rea、vsa=vse+vea分别为航天器相对于SSB 的位置和速度矢量;rse、vse分别为绕飞行星相对于SSB 的位置和速度矢量 ;rea=[rea,x rea,y rea,z]T、vea=[vea,x vea,y vea,z]T分别为航天器相对于行星的位置和速度矢量。
相对绕飞行星建立航天器轨道运动学方程为[5]
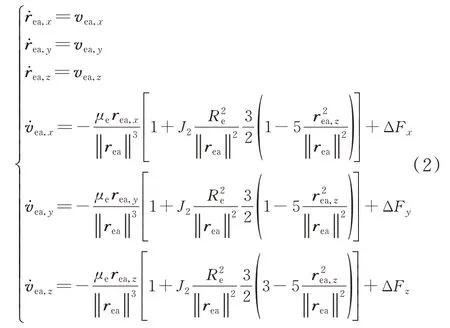
式中:Re为绕飞行星的半径;μe为绕飞行星的引力常数;J2为摄动项系数;ΔF=[ΔFx,ΔFy,ΔFz]T为摄动项矩阵,指的是包括月球引力摄动、潮汐摄动在内的其他摄动力影响。将式(2)简写为

在四维黎曼时空下,航天器的坐标时可由时钟记录的固有时转换得到。在1PN 度规下,忽略星体的自转、扁率以及太阳与SSB 间距,可得到从航天器固有时至SSB 满足纳秒量级精度的时间转换模型[16]:
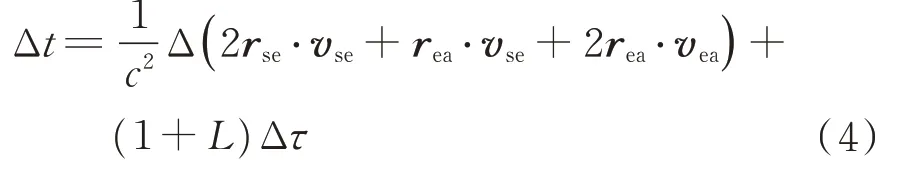
式中:Δτ为星载时钟走过的固有时;Δt为Δτ时间内时钟经历的坐标时;c为光速;等号后的第1 项为Δt时间内运动产生的综合时延;为引力修正因子;μs为太阳引力常数;μe为行星的引力常数;ase为行星绕太阳作椭圆运动的长半轴;aea为航天器绕行星运动的长半轴。
将式(4)简写为
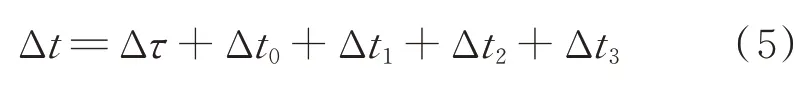
式中:Δt0=LΔτ包含了行星引力产生的频移,称为引力时延;包含了航天器运动以及行星绕太阳运动偏离圆轨道所产生的频移,称为偏轨时延;包含了航天器轨道曲率变化所产生的频移,称为航天器曲率时延;包含了行星轨道曲率变化所产生的频移,称为行星曲率时延;Δt0为长期影响项;Δt1、Δt2、Δt3为周期影响项。
根据式(1)~式(4),航天器的状态模型最终描述为

式中:f(x,τ)=;τ为星载时钟的固有时刻,这是实际飞行任务中可获取的时间状态量;w(τ)为系统的传递噪声矩阵。
1.2 四维观测模型
通常意义下的时间概念是太阳系质心坐标系下的航天器坐标时,而实际中可获取的时间变量是星载时钟原子时,它们之间存在一种转换关系。在高精度要求的情况下,坐标时成为了一个关于航天器状态和原子时变化的新观测量,同时单颗脉冲星仅可以在组合导航中应用,或者作投影方向上的导航算法精度验证,不能实现自主导航。因此,需要引入四维观测模型。
根据相对论定位系统的基本思想和后牛顿引力理论,将脉冲星P(P=1,2,3,4)走过的固有时TP作为直接观测量[13],建立四维观测模型如下:

根据式(7)和式(8),脉冲星导航的四维观测模型简写为

四维观测模型相比传统的三维观测模型,引入了时间状态量,且不必推算标准轮廓的相位,具有更精确的时间估计,更小的相位拟合误差。
2 基于UKF 的脉冲星导航算法
根据式(6)和式(9)得到脉冲星导航系统的离散模型为

式中:wk、vk的协方差矩阵分别为Qk和Rk,且满足
利用UKF 算法进行脉冲星导航滤波的步骤如下:
步骤1时间转换。上一时刻到当前时刻走过的固有时为Δτk−1,根据式(4)可将航天器记录的固有时转换为坐标时,即

步骤2构造采样点。卡尔曼滤波传递状态量的一阶矩和二阶矩信息,对于状态均值及其协方差矩阵Pk−1,选取比例对称采样策略对其进行采样,但在采样前需要保证算法的稳定性。由于协方差矩阵Pk−1存在时间项的极小对角值,在迭代过程中不能保证其对称半正定,需对Pk−1作对称正定化处理:


式中:α为比例缩放因子,可通过调整α取值来调节采样点与中心点的距离;β为函数f(⋅)的高阶项参数;κ涉及高 阶矩的选取,一般 取为0 或3−n,但应确保协方差矩阵传递的半正定性。

式中:(·)i算子为取矩阵的第i列信息。
将采样点展开为

步骤3预测。利用状态模型对每个采样点进行预测,得到

计算状态均值及其协方差矩阵为

计算观测量及其均值为

步骤4更新。观测量与状态量之间的预测协方差阵分别为

滤波器增益为

更新时刻的状态均值及其协方差矩阵为

3 仿真分析
3.1 仿真条件
仿真采用DE405 星历,初始时间为1990 年7 月7 日12 时0 分0 秒,时长为35 d,观测时间间隔为500 s。
本文的导航模型适用于太阳系任一行星的绕飞轨道,这里以绕飞地球高轨为例,其轨道参数见表1。

表1 轨道参数Tab.1 Orbit parameters
选用Arecibo 天文台长期观测的4 颗毫秒级脉冲星,其参数见表2。

表2 脉冲星参数Tab.2 Pulsar parameters
计算机仿真环境为CPU 4 核2.5 GHz,内存8 GB,Matlab 2012b。初始状态误差δx0、初始协方差阵P0、系统噪声协方差阵Qk、观测噪声协方差阵Rk设置如下:
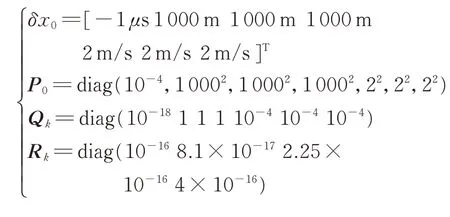
3.2 仿真结果
UKF 滤波后的导航结果如图2所示,导航的位置误差稳定在10 m 量级,时间误差稳定在nm 量级,速度误差稳定在0.01 m/s 量级。下面分别讨论时间转换模型和四维观测模型中的时延项对导航精度的影响。

图2 四维黎曼时空下脉冲星导航模型的估计误差Fig.2 Estimation errors of the pulsar-based navigation model in 4D Riemann space-time
3.2.1 时间转换模型精度分析
时间转换模型的各个时延项在迭代中所占的比重如图3 所示。其中,引力时延Δt0数值最大,达10−5s 量级;偏轨时延Δt1、行星曲率时延Δt3比重相对较小,为10−7s 量级;航天器曲率时延Δt2数值最小,为10−10s 量级。忽略时间转换模型中的任一时延项进行导航,结果如图4 所示。可以看出,忽略Δt0对导航精度的影响最大,达105m 量级;忽略Δt1、Δt3对导航精度的影响相对较小,为103m 量级;忽略Δt2对导航精度的影响最小,为10 m 量级。这表明在时间转换过程中,引力时延、航天器偏轨时延以及绕飞行星曲率时延等因素对导航精度的影响较大,航天器绕行星飞行的曲率变化对导航精度的影响较小。上述分析验证了引入时间转换模型的必要性。

图3 时间转换模型中的时延项比重Fig.3 Proportion of delay items in the time transformation model

图4 忽略时间转换模型时延项的导航定位误差Fig.4 Positioning errors without a time transformation term
3.2.2 四维观测模型精度分析
四维观测模型中的各个时延项在迭代中所占比重如图5 所示。图5 中,引力时延ρ3(r)数值较大,达10−4s 量级,周年视差时延ρ1(r)数值较小,达10−7s量级,脉冲星自行时延ρ2(r)总体上呈增长趋势,在仿真时间内与ρ1(r)达到同一量级。若忽略其中一项进行导航,结果如图6 所示。

图6 忽略四维观测模型时延项的导航定位误差Fig.6 Positioning errors without a time delay term of the 4D observation model
可以看出,忽略ρ3(r)对导航精度的影响很大,达104m 量级;忽略ρ1(r)、ρ2(r)对导航精度的影响较小,为103m级,并且由于脉冲星自行时延有累积增长趋势;忽略ρ2(r)引起的误差按其趋势增长,与图5的结果吻合。上述分析表明,在量测过程中太阳系的引力远大于周年视差效应、脉冲星自行对导航精度的影响。
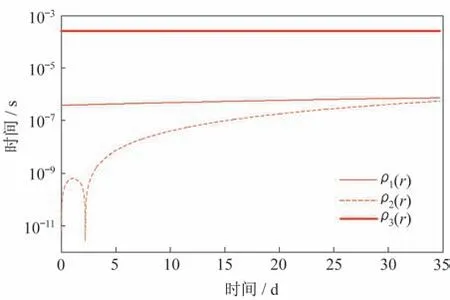
图5 四维观测模型中时延项比重Fig.5 Proportions of delay items in the 4D observation model
4 结束语
本文建立的导航模型考虑了广义相对论的影响,通过引入时间转换模型可适应ns 量级的计时精度,在此基础上分析了导航模型的精度影响因素,为深空探测的工程应用提供了理论参考。同时使用本文建立的导航模型可以简化脉冲星信号处理过程,为脉冲星导航算法提供更精准的模型基础。
