孤岛微电网下的单相H桥并网逆变器系统稳定性分析∗

宗海焕，孙 帅，喻 宙，宗海迥

(1.郑州电力高等专科学校，河南 郑州 450000；2.国家电网有限公司交流建设分公司，北京 100052)

科技社会的发展离不开能源的支撑，在当今能源短缺的时代，电能是一种清洁、便利的能源之一，在当今社会是不可或缺的部分。为了获取电能，能够最大效率地利用现有的能源制造出更多的电能，专家学者已经开发了以太阳能、风能、核能等新能源的能源结构[1－3]。

微电网是由清洁能源、并网逆变器、负载、整体控制系统以及储能设备的总称。在国家电网的大环境中，微电网充当着分支的角色，既能够并网发电，也可以孤岛运行[4]。在进行微电网并入大电网时，一般采用下垂控制对多台逆变器进行控制[5－7]。在下垂控制的基础上，单台逆变器通常采用电压电流双闭环的模式进行控制，给定电压参考值，通过电压外环得到电流内环的给定，再通过电流内环得到与载波比较的调制波[8]。针对并网逆变器的稳定性分析这一问题，有很多专家学者已经做了很多的研究，比如输入－输出稳定性判据[9]、李雅普诺夫稳定性判据[10]、多变量奈奎斯特稳定性判据[11]、无源稳定性判据[12]、阻抗稳定性判据[13]、Bode 稳定性判据(对数判据)等[14]。

本文基于单相并网逆变器的阻抗模型，进而采用电压电流双闭环策略对系统进行控制。通过Bode 图的形式，对如何选择控制器参数进行了分析，用Bode稳定性判据对本文所选择的参数进行验证，同时也用实验波形对并网的电压电流波形进行分析。

1 阻抗模型

微电网分布式发电中，不同单元的并网逆变器的控制一般采用下垂控制进行并联，因而可以等效成一个带有电压源的阻抗模型。

本文以单相H 桥逆变电路作为例子进行说明，如图1 所示为单相H 桥逆变器的拓扑结构图，直流侧的储能设备电压为Udc，其并联电容Cf是DC 侧的滤波器，H 桥逆变器每个开关器件单元采用的是IGBT 反并联二极管结构，交流侧为LC滤波，逆变器的交流输出为Ui，逆变器负载等效为ZL，其电压为uo。

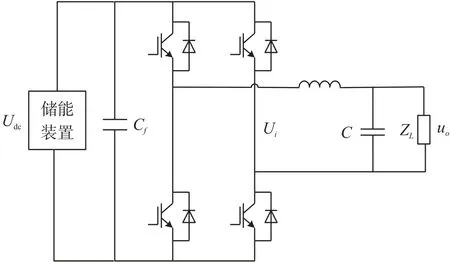
图1 单相H 桥逆变器拓扑

对于图1 中的拓扑电路，一般采用简单的SPWM 调制策略，一般情况下，将调制策略等效为一个简单的线性环节进行分析。众所周知，我国交流电的基波频率为50 Hz，因此调制策略中的调制波频率fr也是50 Hz。当载波频率fs远远大于fr时，对于交流侧的电流而言，逆变电路可以等效为一个线性环节，式(1)为其传递函数:

式中:Uc为三角载波幅值，ur为调制波幅值。

单相H 桥逆变电路的交流侧数学模型为:

将式(2)转换到s域内可以得到式(3)。

由式(3)可以得到单相H 桥逆变电路的开关控制框图如图2 所示。

图2 开环控制框图

采用下垂控制的各种逆变器的控制基本上可以包括:功率控制、电流控制、电压控制，可以得到其控制框图如图3 所示。

图3 控制框图

在图3 中，采样负载电压uo以及电流io，采用虚拟正交矢量法得到输出的功率，进而通过下垂控制获取电压电流双闭环控制策略的参考电压uref，通过闭环控制得到对应的50 Hz 调制波，经过与载波比较得到每个开关器件的控制信号。其中，电压电流双环中的电压环采用PR 控制器，电流环采用PI控制器

式(4)为功率下垂控制方法的下垂曲线公式。

式中:m、n分别为有功与无功下垂系数，f∗和U∗分别为空载电压的频率和幅值。

如图4 所示为电压电流双闭环的具体控制框图，其中，Gv(s)为电压环传递函数，Gi(s)为电流环传递函数，kpwm为调制模块的传递函数。其中Gv(s)和Gi(s)在式(5)和式(6)中给出。式中:kvp为比例系数，kvi为谐振系数，ω0为谐振频率，ωc为控制器带宽，k为电流环比例系数。

图4 电压电流双环控制框图

根据图4 的电压电流双闭环控制框图能够得到uref到uo的闭环传递函数以及等效输出阻抗传递函数Zov(s):

由式(7)和式(8)可以得到相应的戴维南等效模型如式(9)所示，并且基于式(9)可以得到电路如图5 所示。

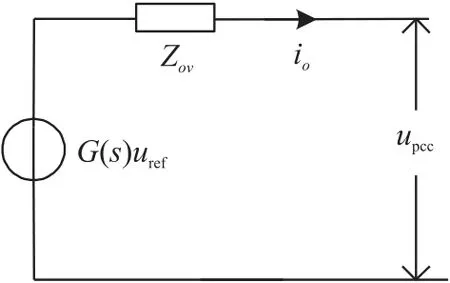
图5 下垂控制逆变器等效电路模型

式中:uref(s)表示参考电压在s域的值，uov(s)表示输出电压在s域的值。

2 控制参数对稳定性影响分析

为了验证控制参数对系统稳定性的影响，本文采用如表1 所示的参数进行了验证。

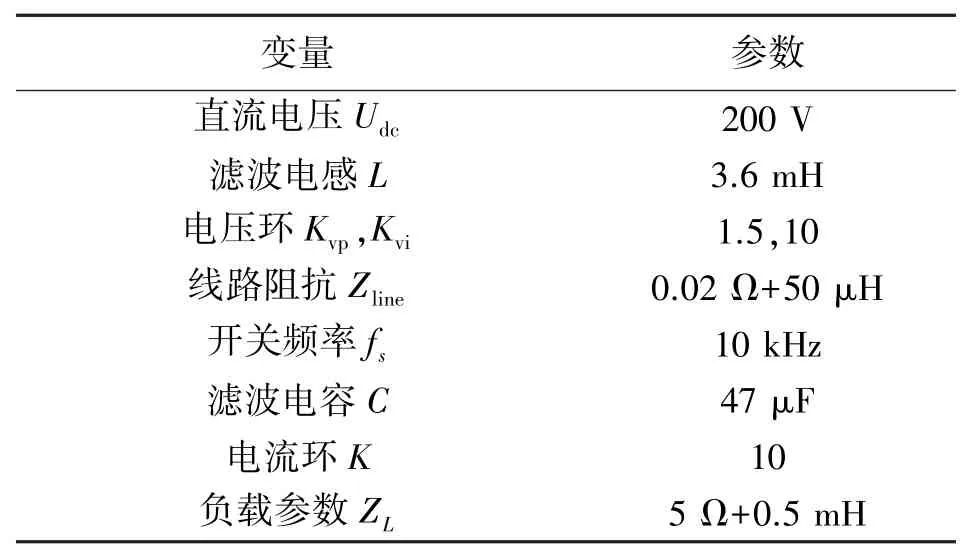
表1 参数

2.1 电压环控制参数对输出阻抗的影响

电压电流双闭环中的电压外环采用PR 控制器，设计参数主要包括比例系数Kvp和谐振系数Kvi，本文将利用逆变器的输出阻抗的Bode 图进行分析参数对系统稳定性的影响。

如图6 所示为比例系数从0.5 增长至2 时的输出阻抗的Bode 图。

图6 Kvp变化时输出阻抗的伯德图

图6 显示，频率较低时，输出阻抗幅值会伴随Kvp的增大而减小，但是相位裕度恰好相反；在中频率时，Kvp的作用主要体现在谐振峰，随着Kvp的减小，谐振峰随之变高，所以需要选取合适的Kvp值避免过高的谐振峰，本文选择1.5。

如图7 所示为谐振系数从1 增长至30 时的输出阻抗的Bode 图。

图7 Kvi变化时输出阻抗的伯德图

图7 显示，Kvi的作用主要体现在50 Hz 处输出阻抗的幅值裕度，其值越大，幅值裕度越大，同时会影响50 Hz 处的带宽，其值越大，跟踪精度越高，因此不能选择过小的Kvi值，本文选择1.5。

2.2 电流环控制参数对输出阻抗的影响

电压电流双闭环中的电流内环采用PI 控制器，设计参数主要包括比例系数Kvp和谐振系数Kvi，本文将利用逆变器的输出阻抗的Bode 图分析参数对系统稳定性的影响。

如图8 所示为比例系数从5 增长至20 时的输出阻抗的Bode 图。

图8 显示，K的作用主要体现在频率较高时输出阻抗的幅值和相位。特别是在50 Hz 附近时，较小的K值会导致较大的谐振峰。所以选择K值时不能过小，本文选择的K值为10。

图8 K 变化时输出阻抗的伯德图

2.3 系统稳定性分析

通过上述的参数选择，通过图4 可以得到式(10)所示的开环传递函数。

利用MATLAB 软件的s-function 功能对其进行Bode 图的绘制，可以得到系统的开环传递函数以及闭环传递函数的Bode 图如图9 和图10 所示。

图9 开环传递函数的伯德图

图9 显示，选择了表1 中的参数之后，系统的开环传递函数的相角裕度是37°，并且具有较高的幅值裕度，这说明系统稳定性较好。图10 显示，系统在50 Hz 的基频附近具备良好的动态跟踪能力。因此说明本文选取的参数比较合适。

图10 闭环传递函数的伯德图

3 实验结果

如图11 所示为系统控制框图，在此基础上使用了硬件平台对上文所述进行验证，H 桥硬件电路如图12 所示。

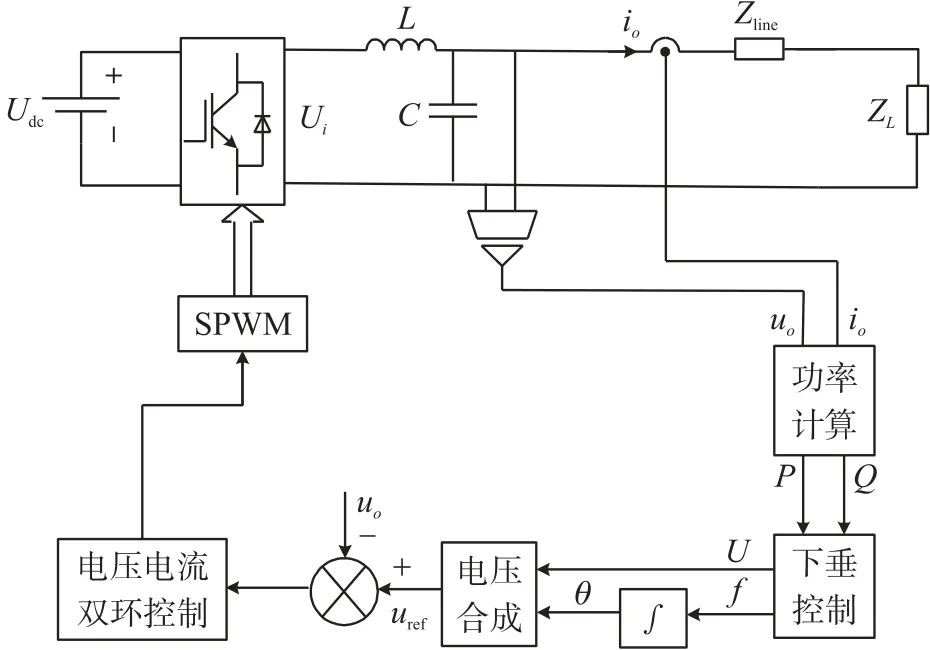
图11 系统控制框图

图12 H 桥硬件电路

如图13 所示为交流侧电压电流波形及其谐波分析实验图。从图中可以看出，电压电流同相位，满足单位功率因数要求，同时电流波形正弦度良好，电流THD 为3.57%，满足国家并网标准。

图13 输出电压电流波形及分析

4 结语

本文针对单台H 桥逆变器并网系统，设计电压电流双闭环控制器，分析参数对系统的稳定性影响，通过Bode 图的方式验证了选择的参数是符合稳定性要求的，实验波形可以证明设计的单相H 桥逆变器符合并网需求。