基于CTA影像数据的迂曲冠状动脉血液两相非牛顿血液动力学分析

王东侠 江 洁 刘 鹤 尹燕伟 胡明成▲

1.北京市丰台中西医结合医院放射科，北京 100072；2.黑龙江省牡丹江林业中心医院感染科，黑龙江牡丹江 157011；3.牡丹江医学院附属红旗医院磁共振科，黑龙江牡丹江 157011

动脉粥样硬化是严重的心血管系统疾病，冠状动脉粥样硬化在心血管系统疾病占很大比例，冠状动脉粥样硬化的形成、发展机制是当前生物力学与医学工程领域的研究热点。血流动力学因素在冠状动脉的形成发展中的作用被越来越多的研究证实[1]。一些学者采用理想的冠状动脉迂曲模型运用单相、多相血流模式研究弯曲动脉的血流动力学指标。相关研究基于理想冠状动脉模型研究发现弯曲部位内侧存在较低的壁面剪切应力分布[2]；有研究通过单相血流模式研究发现在模型最大弯曲处的内侧存在着较高的壁面切应力，与临床观测结果相反[3]。有学者通过螺旋弯曲理想血管模型研究发现血管下底面处红细胞存在聚集的现象有利于促进血栓的形成[4]。理想模型的血流动力学研究存在一定的不足之处，未将真实的血液流动性质完全考虑进去，血液中包括红细胞、白细胞、血小板等微小颗粒，在血液流动中，这些微小血液颗粒容易在血管的弯曲、分叉等部位形成浓度极化现象，红细胞的聚集是动脉粥样硬化的原因之一，红细胞在白细胞对内皮细胞层的附着能力具有显著的促进作用[5-8]；此外真实的冠状动脉模型的结构特性比理想模型更复杂，基于理想模型的血流模拟无法反映冠状动脉的血流真实情况[9]。不仅如此，通过单相血流动力学分析无法实现对红细胞等微小颗粒的运动规律进行观察。血液黏度的流变在血液流动中也具有重要作用，血液黏度分布对红细胞颗粒的运动有着巨大的影响。因此在多相流运动中，血液的非牛顿流体特性应当给予考虑。利用冠状动脉粥样硬化的数值模拟方法分析血流动力学因素，探讨壁切应力等血流动力学指标对冠状动脉动脉粥样硬化的关系。

本文利用真实患者迂曲冠状动脉CTA影像数据进行三维重建，结合计算流体力学与血流动力学理论，考虑血液多相流与血液黏度的非牛顿特性的影响进行迂曲冠状动脉的血流动力学参数分析，分析结果为冠状动脉的动脉粥样硬化形成、发展机制提供参考，为临床治疗提供借鉴。

1 资料与方法

1.1 资料搜集

搜集牡丹江医学院附属红旗医院影像科冠状动脉CTA检查影像数据并以DICOM格式保存，患者性别男，52岁，检查结果为冠状动脉迂曲。患者知情同意并签署知情同意书，经红旗医院医学伦理检查委员会批准同意。

1.2 三维模型重建

将迂曲冠状动脉CTA数据导入MIMICS 21.0（Materialise公司，比利时）软件基于阈值和手动微调完成图像分割，以获得迂曲的三维结构模型。经重建之后的三维模型导入3-Matic 15.0（Materialise公司，比利时）软件中进行三角面片网格优化、光滑、包裹、切除多余枝节和出入口面组，最终获取可以进行有限元网格划分的STL格式模型。见图1。

图1 迂曲冠状动脉三维重建模型

1.3 有限元模型网格划分

迂曲冠状动脉有限元网格采用六面体核心的多面体网格，多面体网格具有计算精度高、与相邻网格之间的连接性非常好的优点。为保证计算精度，边界层为5层加密，增长率1.15。网格划分采用Fluent Meshing软件划分。见图2。

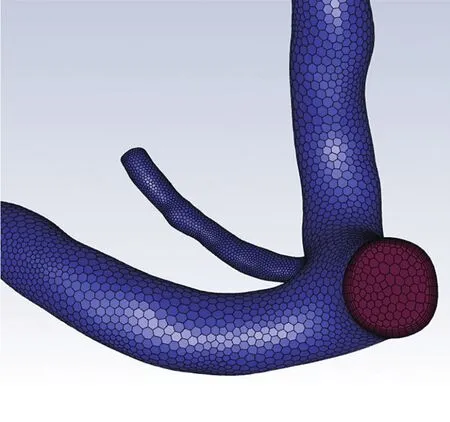
图2 迂曲冠状动脉有限元网格

1.4 血液模型计算设置

血流采用ANSYS Fluent 2019R1软件数值模拟，两种血液模型均采用Carreau-Yasuda剪切变稀的黏度模型，其模型表达式为：

其中， μ为动力学黏度，低剪切黏度μ0和高剪切黏度μ∞分别为0.022 Pa·s和0.0022 Pa·s，时间常数λ为0.110 s，指数z和n分别为0.644和0.392，γ为剪切应变率。

①多相流非牛顿血流模型：采用欧拉模型，主相为血浆，次相为红细胞，血浆密度为1000 kg/m3，黏度为0.0035 Pa·s；红细胞密度为1178 kg/m3，黏度由Carreau-Yasuda模型得到[4]；②单相非牛顿血流模型：血液密度为加权平均得到混合密度1080 kg/m3，黏度由 Carreau-Yasuda模型得到[5]。

两种血流模型数值模拟入口边界条件取正常人的心动周期T为0.8 s，步长为0.01，采用Nichols等通过实验测得的冠状动脉血流速度作为血液入口速度[7]，见图3。血浆和红细胞采用相同的入口速度，设置出口相对压力为零[8]。假设血管壁面刚性无滑移，忽略血管壁的影响，血流控制方程续的三维非定常流动的Navier-Stokes方程。其中在多相血流动力学模拟中，红细胞和血浆采用相同的速度波形[8]。红细胞血液主要由血浆与血细胞组成，其中约95%血细胞为红细胞。动脉血流中红细胞形态大小各异，其中以球形红细胞居多，呈双凹圆盘状。本文的红细胞模型采用双凹圆盘状球形红细胞模型，取最小直径为6 μm，最大直径8 μm，平均直径8 μm[10-16]。为了使流场充分发展，得到稳定的模拟数据，采用第3个周期的计算结果进行讨论分析。

图3 入口速度曲线

2 结果

2.1 多相流非牛顿血流红细胞体积分数分布

图4为多相流模型的红细胞体积分数分布云图（0.12 s）。图中所见红细胞在迂曲冠状动脉分叉部位底壁面处存在明显的浓度极化现象，图5为多相流红细胞体积分数切面分布云图。由图可知，红细胞流动分布集中于管壁分叉区域、管壁外侧，与血流速度分布相反，红细胞在分叉处的聚集现象与分叉处好发动脉粥样硬化、动脉瘤这一现象完全符合，红细胞在分叉处的聚集容易造成血管内皮细胞缺氧，诱导内膜组织增生，血流中血小板发生凝聚并形成血栓斑块，进而导致血液运输通道狭窄，最终形成病变。

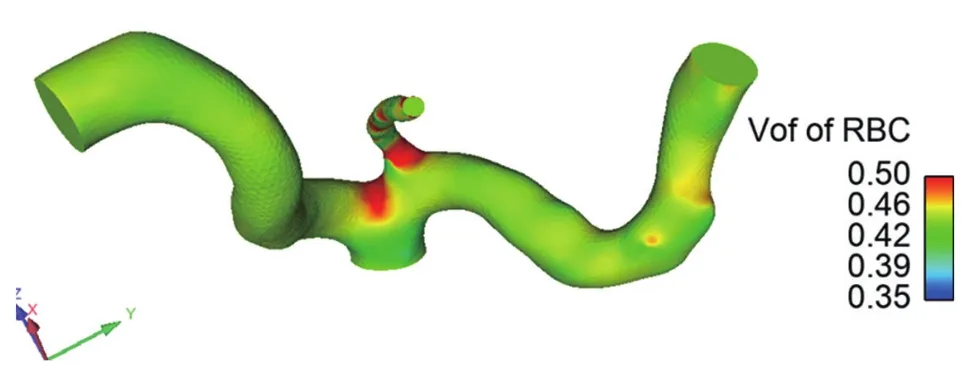
图4 多相流红细胞体积分数分布

图5 多相流红细胞体积分数切面分布

表1为不同典型特征时刻红细胞体积分数的最大值，收缩期红细胞体积分数是初始时刻红细胞体积分数的1.26倍，而舒张期红细胞体积分数是初始时刻红细胞体积分数的1.28倍。

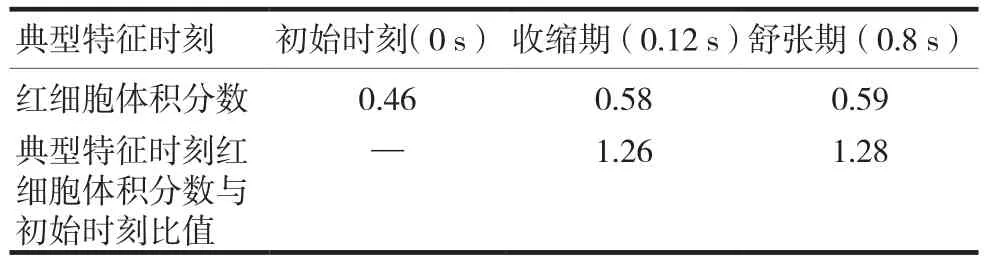
表1 不同典型特征时刻红细胞体积分数的最大值

2.2 冠状动脉壁切应力分布

图6为冠状动脉壁切应力分布（2.4 s），在动脉分叉区域的壁面切应力数值较低，低壁切应力数值为38.7 Pa，红细胞体积分数为0.59，由此可见迂曲冠状动脉的分叉部位红细胞聚集区域呈现低壁切应力分布。

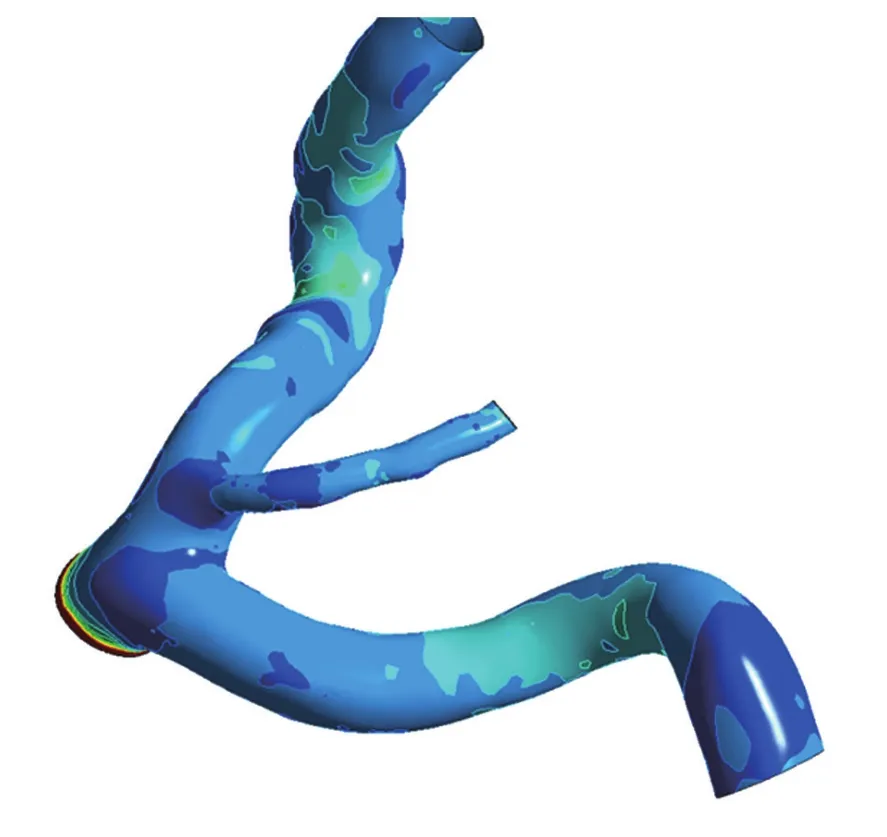
图6 迂曲冠状动脉壁切应力分布

2.3 迂曲冠状动脉单相非牛顿血液流动与多相非牛顿血液流动的速度分析

图7所示位置切面。与多相流血流模型相比，单相流速度都比多相流的速度略快（图8），这种情况在整个血流运动中都存在。而在迂曲冠状动脉多相流运动中，红细胞的血流速度明显比血浆的速度低，越靠近管壁中心线越明显，这种情况和红细胞的颗粒固体流动性质有关，红细胞颗粒在流动过程中，不完全充分流动，具有一定的沉积作用；而血浆的血流速度与单相流速度分布趋呈现出中间速度快，环壁周围速度较慢，速度分布趋于一致。

图7 速度观察直线位置

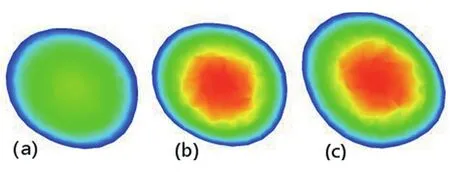
图8 红细胞、血浆、单向流体血流速度分布云图[（a）为红细胞、（b）为血浆、（c）为单项流]

3 讨论

本研究采用1例真实患者迂曲冠状动脉CTA影像数据进行三维重建，在此基础上进行有限元网格划分，应用非牛顿、两相流的数值模拟方法仿真模拟。不足之处在于，研究样本量较少，未考虑重力影响和血管壁运动对血流的影响，也未考虑血液多组分结构的运动特性，在后续的研究中应加大样本量，采用双向流固耦合分析，并结合微观流体的血液多组分成分进行仿真计算。研究结果发现，与单相流相比，多相流可考察红细胞运动的特性及其对脂质浓度极化的血流动力学因素的作用。结果显示红细胞在迂曲冠状动脉分叉部位底壁面处存在明显的浓度极化现象，红细胞的浓度极化现象导致血管内皮细胞缺氧，诱导内膜组织增生，血流中血小板发生凝聚并形成血栓斑块，进而导致血液运输通道狭窄，最终形成病变，这一点符合以前相关研究的结论：动脉粥样硬化好发于弯曲部位。而红细胞聚集区域的壁面剪切应力分布又较低，在此条件下，红细胞聚集更加严重，更易导致病变发生。红细胞的聚集与冠状动脉迂曲的几何特征有密切的关系，在血液流动过程中，在接近管壁外侧，单向流速度要比多相流速度略快，这种情况可能跟红细胞的流动特性关系密切，红细胞运动呈现沉积。多相流的红细胞速度这种特殊现象可能也与冠状动脉迂曲这一特殊结构有直接关系。

综上所述，本研究通过多相流、单向流非牛顿流体的分析，对迂曲冠状动脉的血流动力学指标进行了分析，研究考虑血液黏度非牛顿特性条件下的红细胞运动特性。本研究不足之处在于选取的研究对象只有一个，后续研究应当进行扩展多病例的统计学分析。