水泵全特性曲线的预测及对数值分析的影响
2021-07-16黄亚周建旭
黄亚,周建旭
(河海大学水利水电学院,江苏 南京 210098)
水泵全特性曲线完整地体现了水泵在任意可能运行条件下的流量特性和能量特性,包括可能出现的水轮机工况、泵制动工况、泵工况和反转制动工况的运行特性和过渡特性,是数值模拟分析水泵系统水力过渡过程所必需的重要边界条件[1],即水泵全特性曲线为水泵系统水力过渡过程分析、泵站设计和停泵水锤的计算分析提供了重要的数据支撑,其精度直接影响模拟与分析管路水力瞬变现象,对供水系统的稳定与安全具有重要意义[2-5].通常,水泵全特性曲线由水泵生产厂家提供,生产厂家又是从模型试验得到,利用相似律,将模型试验数据按相似率换算为真机数据,得到水泵的全特性曲线[6].由于水泵全特性曲线试验条件极为复杂,全特性数据难以获取,故利用已有的水泵全特性曲线数据,通过拟合分析来获取某一型号水泵的全特性数据,具有重要的现实意义[7].
目前国内外对水泵全特性曲线的预测方法基本上都是基于Suter曲线的预测分析.预测方法可以分为2类:一是在二维坐标下采用数学变换进行处理;二是在三维空间下利用曲面拟合进行处理.刘竹溪等[8]由实测的水泵全面性能曲线提出了利用三次多项式的拟合建立通用模型.朱满林等[7]、邵卫云等[9]用最小二乘法建立了离心泵全特性曲线二元线性回归预测模型,该预测模型可认为是在二维坐标下的数学变换.刘光临等[10]运用BP神经网络法预测了水泵全特性曲线.胡晓阳等[11]利用Matlab建立三维模型预测水泵全特性曲线.随着计算流体动力学技术的快速发展,也有很多学者开始采用CFD数值分析方法对水泵性能进行研究.欧鸣雄等[12]基于Realizablek-ε湍流模型预测射流泵性能曲线,但是这些方法都过于复杂.文中采用牛顿插值方法,利用现有的水泵资料预测任意比转数水泵的全特性曲线,方法简单,便于数值计算.同时,考虑到一般水泵厂家会提供水泵基本特性数据,在采用比转数作为自变量来预测水泵全特性曲线的基础上,充分利用水泵的基本特性数据来修正水泵全特性曲线,以进一步提高水泵全特性预测分析和泵系统过渡过程计算分析的精度.
1 水泵全特性曲线预测
水泵全特性曲线为水泵机组在任意可能的运行工况下,结合水泵扬程H、流量Q、转速n等参数,绘制出的水泵实际运行工况中各参数的变化规律,包括水泵工况、水泵制动工况、水轮机工况、水轮机制动工况.当水泵正常工作时,水泵扬程、流量、转速、功率都取为正值,即为水泵工况.
水泵全特性曲线是在流量和转速的坐标系中表示出水泵所有的运行工况和可能的过渡工况,以及这些工况下各工作参数关系的曲线,并绘出水泵扬程等值线和力矩等值线.水泵全特性曲线可直接应用于水锤的图解计算分析,比较直观、简便,但是由于这种水泵全特性曲线涉及的参量较多,曲线复杂,难以用数学式解析表达,不能直接应用于水泵过渡过程的数值计算分析.1965年,MARCHAL等[13]根据泵的相似原理,通过数值换算的方法提出新坐标体系,将水泵四象限特性在[0,2π]区间内变换为2条无因次曲线,该方法物理意义明确且利于数学描述,即将水泵参数全部换算为量纲为一的参数.
(1)
式中:T为水泵的转矩;下标R表示额定工况下的参数.
基于上述参数,提出新的坐标系为
(2)
采用新的坐标系,水泵全特性曲线转化成便于水泵系统过渡过程计算分析的表达形式,在保证数值计算精度的前提下,MARCHAL将Suter曲线离散分成88段,共89个数据点,作为反映水泵流量特性和能量特性的离散数据,应用于水泵系统过渡过程的数值计算分析,确定水泵的瞬态参数时采用直线代替两点之间的全特性曲线进行插值计算.
1.1 全特性曲线预测方法
预测不同比转数水泵全特性曲线的数值方法和数学模型较多,最常用的水泵全特性曲线的预测拟合方法是采用拉格朗日方法或者多项式拟合.当插值节点增减时拟合计算全部要重新进行,特别是当前期插值的水泵全特性曲线初始数据比较多,后期又加入一些基础数据时,采用上述拟合方法则需要重新计算,计算量大且不方便.因此文中采用牛顿插值多项式来推求不同比转数下的水泵全特性曲线,当后期加入拟合分析的基础数据时,根据牛顿插值方法的特性,不用重新拟合计算,可直接计算均差,修正预测值,减少计算量.
1.1.1 牛顿插值方法
牛顿插值多项式中包含了函数的均差.定义函数f(x)的k阶均差为
f[x0,x1, …,xk]=

(3)
均差有如下的基本性质
1)k阶均差可表示为函数值f(x0),f(x1),…,f(xk)的线性组合,即
(4)

这个性质可以表明,均差与节点的排列次序无关,称为均差的对称性,即
f[x0,x1, …,xk]=f[x1,x0,x2, …,xk]=
…=f[x1,…,xk,x0].
(5)
2)由均差定义和性质(1)可以得到
f[x0,x1, …,xk]=

(6)
为了便于计算节点的均差,可以采用表1的均差表.

表1 均差表
当n=1时,记此时线性插值多项式为P1(x),它满足条件P1(x0)=f(x0),P1(x1)=f(x1),则P1(x)可以表示为
(7)
可认为零次插值P0(x0)=f(x0),同时联立式(3)和式(7),则n=1情况下的插值多项式可表示为
P1(x)=P0(x)+f[x0,x1](x-x0)=
f(x0)+f[x0,x1](x-x0).
(8)
同理可得n=2情况下的二次多项式为
P2(x)=P1(x)+f[x0,x1,x2](x-x0)(x-x1)=
f(x0)+f[x0,x1](x-x0)+
f[x0,x1,x2](x-x0)(x-x1).
(9)
根据均差定义节点x0,x1,…,xk∈[a,b],将x看成[a,b]上一点,可得
f(x)=f(x0)+f[x,x0](x-x0),
f[x,x0]=f[x0,x1]+f[x,x0,x1](x-x1),
⋮
f[x,x0,…,xn-1]=f[x0,x1,…,xn]+f[x,x0,…,xn](x-xn),
(10)
将式(10)中后式依此代入前式就可以得到
f(x)=f(x0)+f[x0,x1](x-x0)+f[x0,x1,x2]·
(x-x0)(x-x1)+…+f[x0,x1,…,xn]·
(x-x0)(x-x1)…(x-xn-1)+f[x,x0,x1,…,xn]ωn+1(x)=Pn(x)+Rn(x),
(11)
式中:
Pn(x)=f(x0)+f[x0,x1](x-x0)+f[x0,x1,x2]·
(x-x0)(x-x1)+…+f[x0,x1,…,xn]·
(x-x0)(x-x1)…(x-xn-1),
(12)
Rn(x)=f[x,x0,x1,…,xn]ωn+1(x),
(13)
称Pn(x)为牛顿均差插值多项式.
1.1.2 牛顿插值法预测水泵全特性曲线
基于实测的对应特征比转数的水泵全特性曲线,利用牛顿均差插值多项式就可以来推求任意比转数的水泵全特性曲线.目前已知的实测的水泵全特性曲线由霍兰特试验得到的比转数为25,147,261的Suter曲线[14],转换为国家标准比转数表达式,则比转数分别为91.25,536.55,952.65,如图1所示.

图1 实测3种比转数的水泵全特性曲线
利用这3条实测的全特性曲线就可以计算其比转数的一阶、二阶均差,从而可以用牛顿插值方法预测出其他比转数的水泵Suter曲线.为了方便计算,可列计算表如表2所示.

表2 WH曲线插值均差表
通过表中数据就可以得到水泵比转数为NS的全特性WH曲线值为
WH(x)=WH1(x)+f[NS1,NS2](NS-NS1)+
f[NS1,NS2,NS3](NS-NS1)(NS-NS2),
(14)
同理可得全特性WB曲线为
WB(x)=WB1(x)+f[NS1,NS2](NS-NS1)+
f[NS1,NS2,NS3](NS-NS1)(NS-NS2).
(15)
考虑到后期增加不同特征比转数水泵全特性曲线数据的可能性,假定预测样本数据增加1条比转数为NS4的全特性曲线,根据式(14)和式(15)可得精度更高的WH*,WB*曲线,如下式所示.
WH*(x)=WH(x)+f[NS1,NS2,NS3,NS4](NS-NS1)(NS-NS2)(NS-NS3),
(16)
WB*(x)=WB(x)+f[NS1,NS2,NS3,NS4](NS-NS1)(NS-NS2)(NS-NS3).
(17)
1.2 全特性曲线的修正

由水泵铭牌可知水泵的额定流量QR,额定水头HR,额定效率ηR和额定转速NR.根据试验获取基本特性曲线的前提条件,水泵转速N=NR,由式(1)可得水泵Suter曲线中量纲为一的转速α=1,则式(2)中Suter曲线坐标系变成式(18)
(18)

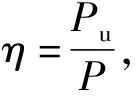
(19)
从而得到Suter曲线量纲为一的转矩为
(20)
经过算例分析表明,水泵基本特性曲线中流量与效率Q-η曲线中第1个点(Q1,η1)为原点,即Q1=0,η1=0,不能直接代入式(20).因此需要转化式(20),将轴功率P=Tω代入式(20)中可得
(21)
通过读取水泵基本特性流量与轴功率Q-P曲线中Q=0时的P值,代入式(21)中就可以反演计算得到Suter曲线中的第1个数据点,或者将反演计算得到的Suter曲线作图延伸出第1个点.
由于式(21)中读取P值时,水泵基本特性流量与轴功率Q-P曲线中P值绝对值较大,网格刻度相对较大,容易给读数带来较大的误差,因此除了第1个点推荐使用式(21),计算Suter曲线上其他数据点时,用式(20)相对比较精确.因为水泵基本特性曲线是厂家针对某一特定型号的水泵通过试验获得的,相对于预测的同一轮系比转数相等的Suter曲线而言,反演计算并且修正得到的Suter曲线更精确,能够准确地揭示水泵正常运行工况下的水力特性.
2 算例验证分析
某一泵系统工程中,管路净扬程为45 m,总长为28.6 km.管道糙率为0.012,水泵的比转数为219,水泵额定流量为15 m3/s,额定扬程为60 m,额定转速为333 r/min.系统布置简图见图2.

图2 泵系统布置简图
结合图2所示的泵系统工程,计算分析工况包括:
1)正常运行工况.
2)抽水断电工况.水泵额定转速下正常运行,突然事故断电停机.
2.1 牛顿插值结果分析
分别采用拉格朗日插值和牛顿插值方法拟合计算得到水泵Suter曲线,如图3所示,分别采用相应的水泵全特性拟合曲线作为水泵边界条件计算分析泵系统的水力过渡过程.
图4为正常运行工况下从取水口到出口水库的管道测压管水头线,图中NL为位置编号.图5给出了抽水断电工况下水泵出口测压管水头和流量的变化曲线.
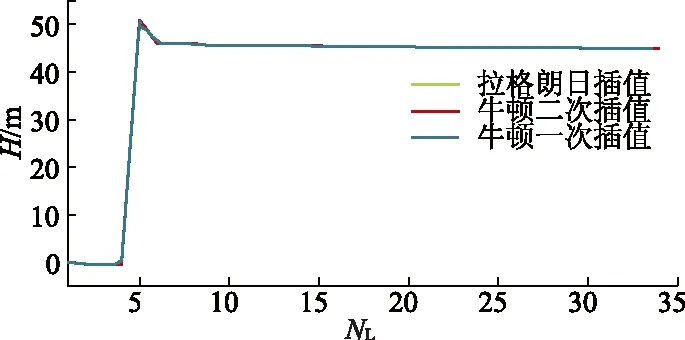
图4 水泵工况正常运行时管线测压管水头
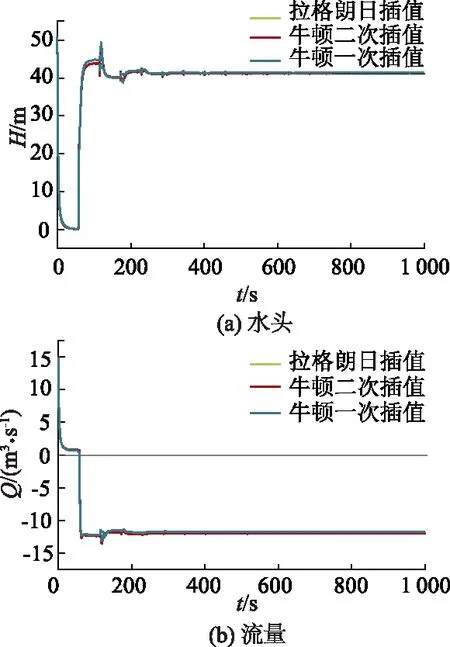
图5 事故掉电工况水泵出口测压管水头和流量
图3分析表明:基于考虑二阶均差的牛顿二次插值的水泵全特性曲线与拉格朗日插值得到的曲线一致,而仅考虑一阶均差的牛顿一次插值曲线局部存在较小的偏差.
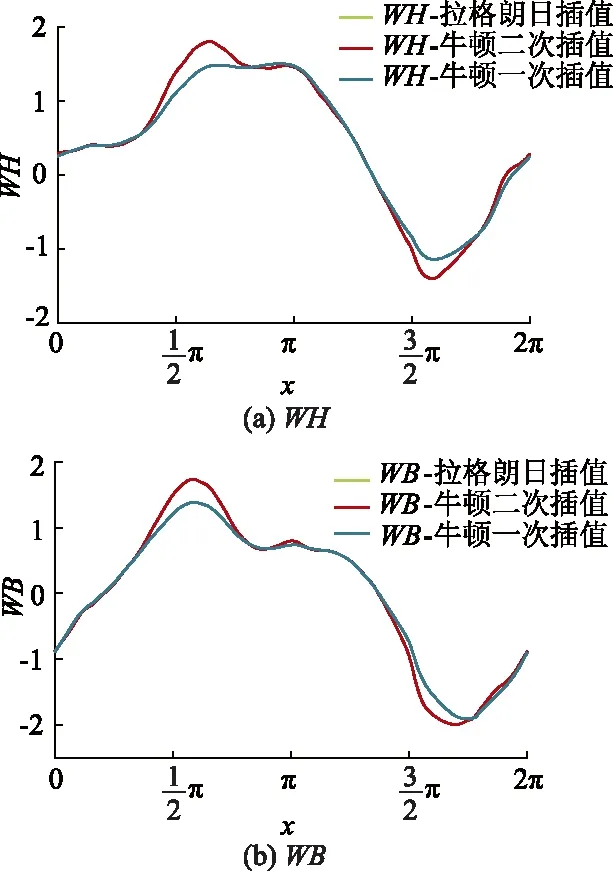
图3 不同插值方法下的水泵Suter预测曲线
由图4,5可看出:水泵在正常运行和事故掉电2种工况下,不同方法计算得到的管道沿程测压管水头线几乎重合,水泵出口测压管水头和抽水流量的动态过程线规律一致,偏差很小.其中拉格朗日插值方法与运用二阶均差的牛顿二次插值方法得到的结果一致,与运用一阶均差的牛顿一次插值方法得到的稳态沿程水头相差最大为0.09 m,瞬态水泵出口水头相差最大不超过1.94 m,流量相差最大为0.38 m3/s.由于目前大多数泵系统工程在计算水力过渡过程中所使用的水泵Suter曲线都是通过拉格朗日方法得到,因此对比图3,4中的基于拉格朗日算法的分析表明,基于牛顿插值算法得到的水泵全特性数据是可靠的.因在牛顿插值算法中,均差与节点的排列次序无关,可认为牛顿插值方法具有承袭性,随着预测的数据资料的增加,可在原来计算的基础上依次加上均差多项式,不用重新计算.相对于拉格朗日算法,牛顿插值算法得到的水泵全特性Suter曲线的修正更加方便,数据的计算量更少.
2.2 基于牛顿插值的反演修正结果分析
利用水泵已有的基本特性曲线反演计算得到的Suter曲线中水泵正常运行工况下的数据点,替换相应工况区原拟合数据,得到图6所示的水泵Suter曲线.

图6 插值预测与局部修正后的水泵Suter曲线
在水泵基本特性曲线上绘制供水工程管路特性曲线得到水泵的工作点,如图7a所示,分别考虑修正后和修正前的水泵Suter曲线作为边界条件,采用一维特征线法计算分析泵系统正常运行时水泵的参数,包括水泵的抽水流量和抽水扬程,在图上标示如图7b所示.
通过分析图6和图7表明:根据水泵基本特性曲线修正后的Suter曲线,在正常水泵工况区间的数据与用牛顿插值得到的拟合值存在一定的偏差.由于水泵基本特性曲线通过试验获取,经过数值变换修正后的水泵Suter曲线数据较修正前更准确地模拟水泵的实际特性.图7b可以清晰地表明,分别考虑修正前后的水泵Suter曲线,数值计算水泵稳态时得到的工作点,对应的运行参数存在明显的偏差.
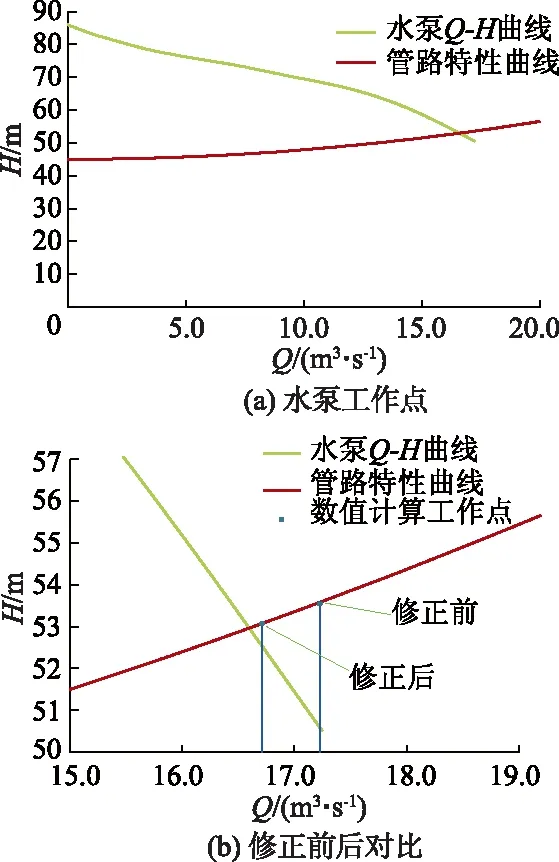
图7 基于修正前/后Suter曲线的水泵工作点图解分析
3 结 论
1)基于考虑二阶均差的牛顿插值算法预测水泵Suter曲线与拉格朗日插值结果一致,表明基于牛顿插值算法的水泵全特性曲线预测方法是合理可靠的,而且牛顿插值算法的特性便于后续增加样本曲线的修正.
2)依据试验获得的水泵基本特性曲线,进一步反演修正水泵Suter曲线中水泵工况区的水力特性,以更准确地模拟水泵的实际特性.利用修正后的水泵Suter曲线进行水泵工况的稳态数值计算,更接近于水泵基本特性曲线图解法得到的结果.
3)考虑牛顿插值算法的水泵全特性曲线预测方法,并利用水泵基本特性曲线来修正水泵全特性曲线的水泵工况区数据,可以提高泵系统水泵稳态计算工作点精度,并较准确地反映水泵全工况的流量特性和能量特性,提高泵系统过渡过程计算分析的精度.
