低温等离子体增强催化氨合成机理的 一维流体动力学模型
2021-07-15刘红梅庄池杰
陈 赦 刘红梅 吴 婷 汪 沨 庄池杰
(1. 湖南大学电气与信息工程学院 长沙 410082 2. 电力系统及大型发电设备安全控制和仿真国家重点实验室(清华大学电机系) 北京 100084)
0 引言
氨是目前对世界经济有着重大影响意义的第二大工业生产化合物。由于氨具有较高的氢密度,且易于液化,它有潜力成为一种安全储存和运输氢能的介质。工业上采用哈伯工艺法生产氨气[1]。这个过程需要400~600℃的高温来激活催化剂,使氮氮三键断裂,并且采用20~50MPa的高气压使得平衡向有利于氨生成的正反应方向进行[2]。此外,它每年还会消耗掉全球2%的能源,并且排放超过3亿t的CO2[3]。因此,研究者们一直在试图寻找创新性替代方法,包括生化方法[4]、催化热解[5-6]和等离子体催化[7-8]。其中,等离子体催化合成氨在能源、化工等领域显示出广阔的应用前景[9-11]。
低温等离子体中含有分子、原子、带电粒子、处于激发态和亚稳态的活性粒子等。这些粒子有利于克服关键反应的能量障碍,在等离子体增强催化氨合成方面发挥着重要作用。等离子体与催化剂之间的相互作用受很多参数的影响。文献[12-14]在探寻具有等离子体协同作用的高效催化剂以及优化参数和反应器设计方面做了大量的实验。文献[7, 15-18]分别采用类似羊毛状的铜电极,α-Al2O3、钌、膜状氧化铝管等作为催化剂,使得氨产量提高。实验结果显示,电子密度、电子温度和电场强度等属于放电过程中的关键参数[19]。然而,很难通过实验直接测量这些参数[20-22]。
为了深入揭示等离子体催化的机理,有必要通过数值模拟来进一步研究等离子体协同催化剂合成氨的机理。零维等离子体动力学模型是化学反应路径和粒子数值模拟的有力工具,有利于揭示关键反应和粒子的微观演化机理[23-24]。P. Mehta等[25]建立了一个基于密度泛函理论的微观动力学模型。分析得到氮气的分解是速率控制步骤。G. Akay等[26]提出一些反应过程中的关键粒子,包括H、H2、N(4S,2D,2P)和N2(A3Σu+),它们促进了氨的合成。E. Carrasco等[27]建立了低压(0.8~8Pa)下的零维动力学模型来研究中性粒子和离子的演化情况。金属壁上的NH3主要是由原子N和含氮自由基的连续加氢反应产生。J. Shah等[28]也建立了一个低压(34.66Pa)射频等离子体中氨合成的零维动力学模型,指出速率控制步骤是在催化剂表面NH2(S)的生成。J. Hong等[29]利用大气压下的零维动力学模型研究等离子体催化合成氨的反应。结果表明,高反应性的N(S)和H(S)主要是由分子的分解吸附产生。
以往的研究大多是采用零维等离子体动力学模型,研究者主要是研究放电等离子体中影响氨合成的关键化学反应步骤及重要粒子数的演化特性。如电场强度和电子密度在仿真中作为输入参数[29]。本文建立了一维等离子体流体动力学模型。可以显示等离子体反应器中电场、电子温度和电子密度的空间分布。此外,还分析了外加电压、初始氮气与氢气比例和催化剂表面活性位点数目对氨合成的影响。本文将详细解释在不同条件下等离子体微观参数的变化,即电场、电子温度和电子密度的变化。这些微观参数对研究等离子体促进NH3合成的最佳反应条件具有重要意义。
1 模型介绍
1.1 模型反应粒子体系
该模型考虑了47种不同的粒子和379种反应[29]。模型中考虑的气相和表面粒子见表1,包括电子,基态分子和原子,处于振动激发态和电子激发态的分子,正负离子和表面吸附粒子N(S), H(S), NH(S), NH2(S)。假设NH3(S)在表面生成后会立即脱附形成NH3。

表1 模型中考虑的气相和表面粒子Tab.1 Gas phase and surface species in the model
综合文献[27-31]模型中的反应类型,本文模型 的气相反应包括:①电子的碰撞激发和电离反应;②振动激发和去激发反应;③不同激发态分子之间的振动-平动能转化或振动-振动反应;④电子激发和振动激发的N2或H2分子与反应器壁之间的弛豫反应;⑤电子激发与振动激发分子间的转化反应;⑥分子间的分解电离反应;⑦离子与分子之间的反应;⑧电子与离子之间的复合反应;⑨3个气相粒子之间的三体反应;⑩H-离子的产生与损失反应。
表面反应包括:①原子和NHx自由基在催化剂或壁表面的直接吸附,在不同催化剂表面具有不同的吸附系数;②表面吸附粒子与气相原子或分子间的雷迪尔(Eley-Rideal, E-R)反应;③两个表面吸附粒子之间的朗格缪尔-欣谢尔伍德(Langmuir- Hinshelwood, L-H)反应;④基态或激发态分子的分解吸附;⑤解吸。整个反应过程中,壁或表面的温度被假定与气体温度相等。
1.2 等离子体流体动力学模型
等离子体流体动力学模型耦合了电场的泊松方程、中性和带电粒子的连续性方程和平均电子能量密度方程。为了简化计算,假设电子能量服从麦克斯韦分布,利用截面数据计算电子碰撞反应的速率系数。通过求解迁移扩散方程得到电子密度和平均能量。
低温等离子体中电子的连续性方程为
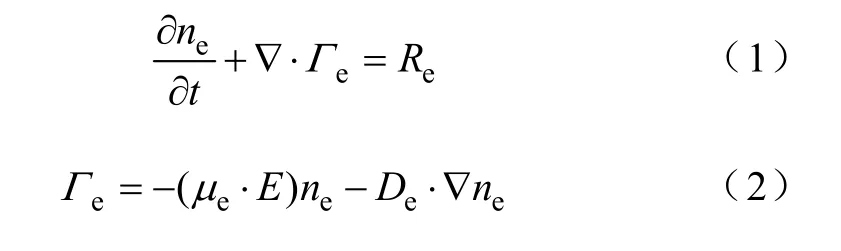
式中,ne、eΓ分别为电子密度和电子通量;eμ为电子的迁移率;E为电场强度;eD为电子的扩散系数;eR为电子的源项,也就是等离子体化学中电子产生率与损失率的总和,可表示为

式中,cj为反应式中对应粒子的化学计量系数;kj为反应j的速率系数;Nm为总的中性粒子数密度。
其他粒子的连续性方程可表示为
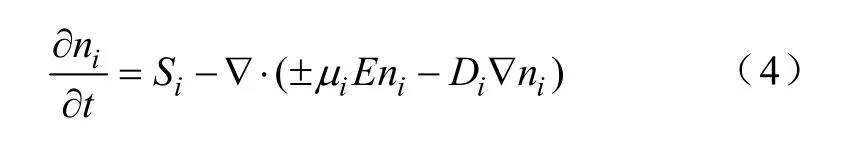
式中,ni为其他正负离子的数密度;iμ和Di分别为迁移和扩散系数;Si为对应粒子的源项,它与不同的反应系数和反应途径(电离、吸附、电子与正离子的复合以及负离子与正离子的复合等)有关。
低温等离子体中的平均电子能量密度方程可以表示为
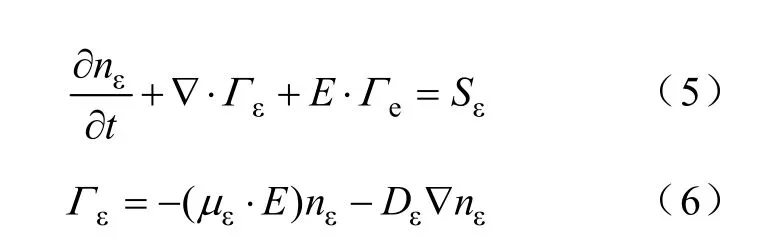
式中,nε为电子能量密度;Гε为电子能量通量;Sε为电子能量的源项,它是由于非弹性碰撞导致能量的增加或损失。
最后,利用泊松方程[32-33]计算等离子体内的电场分布,有
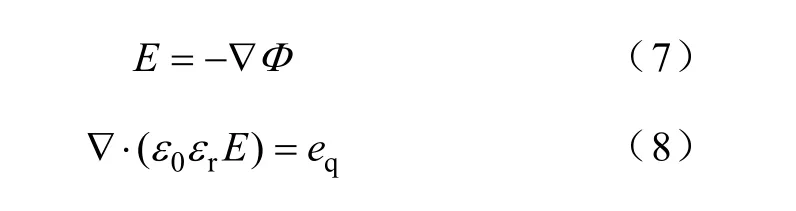
式中,qe为电荷密度,可以通过每个粒子的化学反 应方程式来计算;0ε为真空的介电常数;rε为物质或气体的介电常数;Φ为静电势。
一维仿真模型示意图如图1所示,利用一维模型来模拟大气压下反应器中两个极板之间放电等离子体中发生的化学反应。表面反应假定发生在上下的两个平行板电极上,以模拟催化剂的作用。其中,两侧的两个端点代表两平行板电极,上极板端点1的边界条件为接负的电压,下极板端点2的边界条件为电势为0,上下极板之间的距离为放电间隙长度5mm,回路电源串入镇流电阻,反应腔内的气体温度固定为400K。
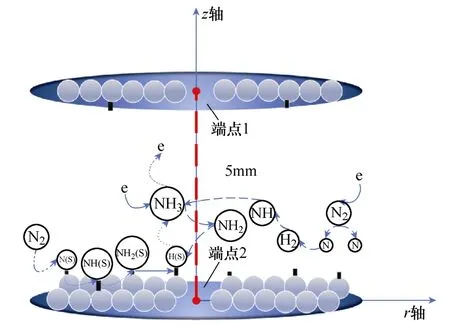
图1 一维仿真模型示意图Fig.1 Schematic diagram of 1D simulation model
通过一维模型可以直观地显示电场强度、电子能量等其他微观参数的空间分布情况,便于更好地观测等离子体特性和揭示低温等离子体增强氨合成机制。值得注意的是,在典型的填充床式介质阻挡放电(Dielectric Barrier Discharge, DBD)反应器中,催化剂填充在整个反应器的放电空间。由于一维模型无法等效填充催化剂的影响,本文模型假设在两个平行板上发生催化表面反应,即金属电极同时发挥催化剂的作用[7-8]。同时,为了模拟较大表面积的催化剂的影响,在3.3节中增大了活性位点密度,等效于增大了催化剂的表面积。但一维仿真模型与真实等离子体反应器催化表面仍存在差异。二维模型或三维模型更有利于研究等离子体与催化表面间的耦合作用,但这些模型非常复杂。本文通过简化几何结构以减小计算量,尽管一维模型有一定的局限性,但仍然可以较好地探究等离子体催化氨合成过程中气相和表面反应的机理。
2 仿真结果
典型仿真条件为一个大气压,温度为400K,初始电子密度为1.1×1014m-3,N2∶H2=1∶2,采用Fe催化剂,施加8.2kV的负直流电压,考虑了合成氨的所有等离子体气相和催化表面反应。多相反应中NH3的产生和损失速率如图2所示。图2a和图2b显示了沿放电间隙对称轴上的氨气的产生与损失速率随时间的变化规律。仿真发现,产生氨的最重要的表面反应机制是表面吸附氢H(S)与吸附的自由基NH2(S)之间的L-H反应,其次是NH2和H(S)的E-R反应。在气相反应中,NH自由基,H2与另一个H2或N2之间的三体反应对氨合成的贡献较大。气相反应和表面反应共同促进了氨气产量的提高。NH3分子损失的主要机理是:与电子碰撞分解产生NH2自由基、H原子以及NH自由基和H2分子,其次是NH3与H原子的反应。这些中间的NHx自由基通过表面或气相反应再次循环参与氨的合成。NH2(S)是氨合成的最重要的表面吸附粒子。从图3a和图3b中可以看出,NH2(S)主要是由NH(S)与H(S)之间的L-H相互作用产生,其次是NH与H(S)之间的E-R相互作用。NH2(S)的主要损失路径是与H(S)或H原子反应生成NH3。
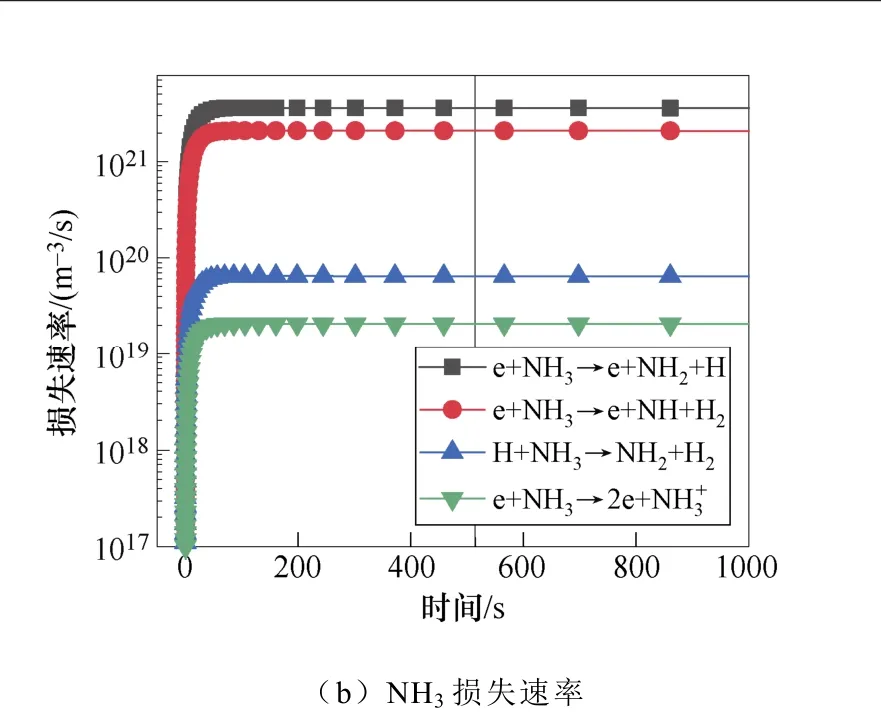
图2 多相反应中NH3的产生和损失速率Fig.2 The production and loss rate of NH3 in heterogeneous reaction
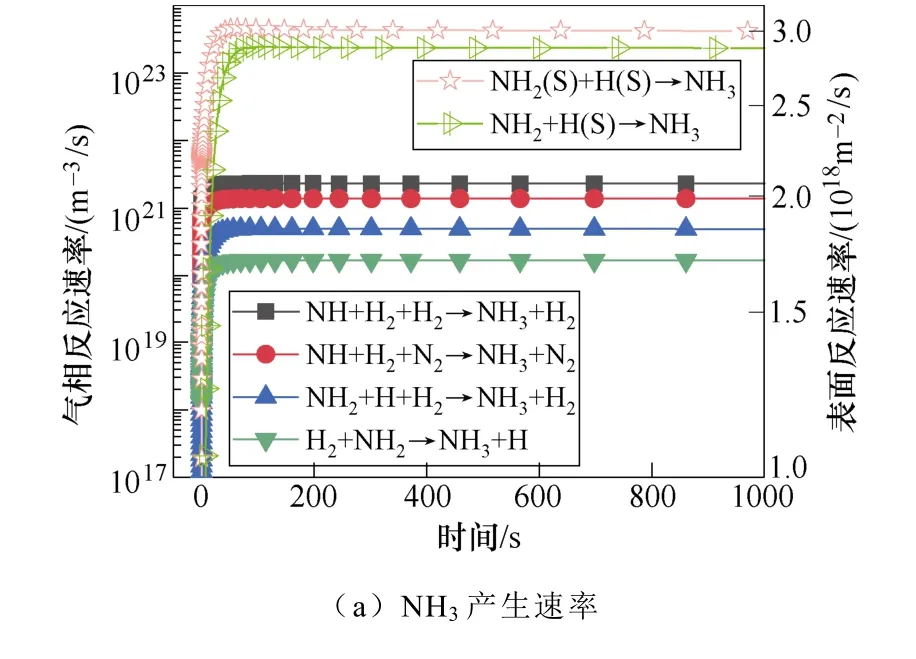
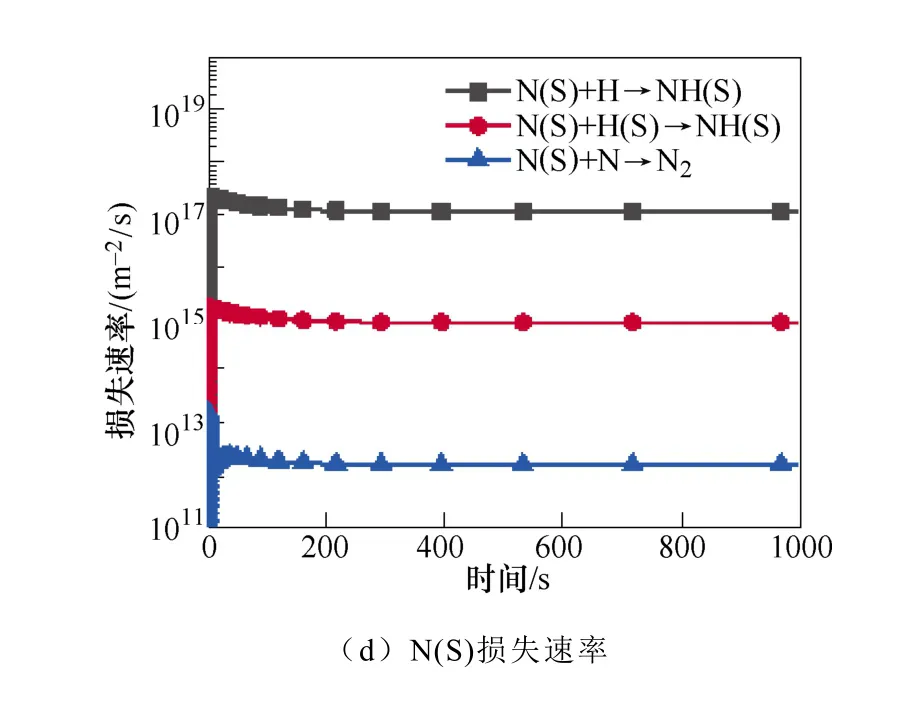
图3 表面反应中NH2(S)和N(S)的主要产生和损失速率Fig.3 The main production and loss rate of NH2(S) and N(S) in surface reaction

N(S)是限制氨合成的关键粒子NH(S)生成的重要粒子,进而限制了氨的合成。如图3c和3d所示,N(S)主要是由基态或振动激发态的N2分子的分解吸附产生。在低温等离子体环境中,有大量的振动激发态N2分子。然后N(S)与H原子反应生成NH(S)。
基于1维流体动力学模型的仿真结果,等离子体催化氨合成的主要反应总结如下:

合成氨的关键反应示意图如图4所示,NH为关键的气相粒子,它与H2以及另一个中性粒子间的三体反应,对合成氨的贡献率达到62.9%,而激发态的H2*与N的反应对NH有70.7%的生成贡献。在表面催化反应中,NH2(S)与H(S)之间的反应对氨生成的贡献较大,达到10.7%。而NH2(S)主要是在NH(S)的参与下反应生成,而N(S)通过与H反应促进粒子NH(S)生成,其贡献率高达98.1%。N(S)主要由基态N2的分解吸附产生,此外,振动激发态N2(v)的分解吸附是N(S)生成的额外途径,贡献率为8.4%。在NH3的损失反应中,有62.3%主要是和电子碰撞分解生成了NH2。

图4 合成氨的关键反应示意图Fig.4 The key reaction mechanism of ammonia synthesis
3 讨论
3.1 外加电压对氨合成的影响
如图5所示为外加电压对NH3数密度的影响。当电压从6.8kV增加到7.7kV时,氨气产量从9.6× 1014cm-3增大到7.1×1016cm-3。当电压超过7.7kV时,氨气产量开始下降。在J. Hong等[13]的实验中,随着电压从12kV增大至14kV,氨气的产量从2.5× 1016cm-3增大到1.1×1017cm-3。在本文仿真模型中,在6.8~7.7kV的电压下,氨气产量随着电压的升高逐渐增加。仿真与实验的结果对比都表明,增大外加电压,增加了反应器中反应电子的密度和能量,有利于氨气的产生。
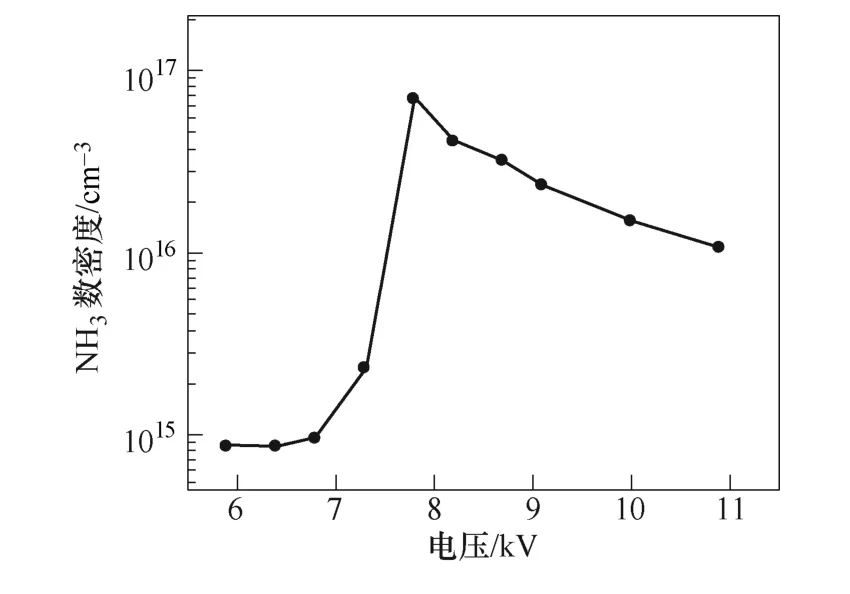
图5 外加电压对NH3数密度的影响Fig.5 Concentration of NH3 as function of applied voltage
不同电压下的氨的产生和损失速率如图6所示,为了方便比较,将气相反应和表面反应分别乘以反应的体积和面积,统一为单位时间内产生的氨气量。从图6a和图6b可以看出,当施加电压从6.8kV增加到7.7kV的过程中,气相和表面反应中氨气的产生速率均迅速增加,而图6c中氨气分解的速率相对较低。因此,氨的净产量增加。然而当外加电压从7.7kV增加到10.9kV时,氨气的产生速率增加了一个数量级,而氨气的损失速率增加了大约3个数量级。随着电子能量的增加,电子碰撞NH3分子导致其分解的速率也随之增大,主要是分解为NH2和H(e+NH3→e+NH2+H),以及分解为NH和H2(e+NH3→e+NH+H2)。因此,在较高的电压条件下氨气的产量反而降低。
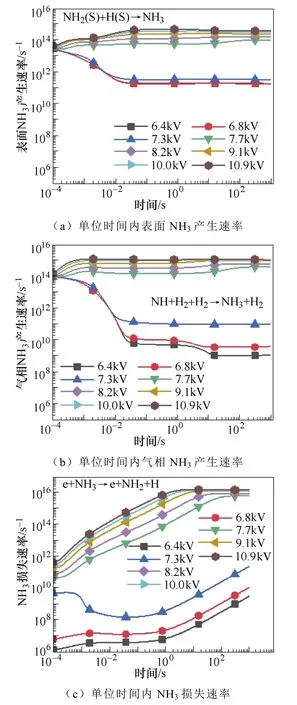
图6 电压对单位时间内表面和气相NH3产生速率 以及损失速率的影响Fig.6 The influence of the voltage on the surface and gas-phase production and loss rate of ammonia per unit time
施加电压对电场和电子温度及电子密度的空间 分布的影响如图7所示。图7a为施加电压对等离子体中电场的空间分布的影响。当施加电压为7.7kV时,放电间隙中的场强范围在80~84Td之间。A. Bogaerts等[31]分析了在不同约化电场下的N2分子在激发、电离和分解等过程中所消耗的电子能量的占比。文献揭示了当约化电场分布在30~85Td之间时,N2分子的振动激发是电子碰撞主要的能量去向。文中的80~84Td处于文献的电场范围内,因而有利于产生大量的振动激发态N2分子。振动激发态的N2分子有利于克服反应的能量势垒进而形成N(S)[25]。N(S)主要由基态或振动激发态的N2分子的 分解吸附产生。N(S)可以连续与H原子反应形成NHx,有助于促进NH3的合成。
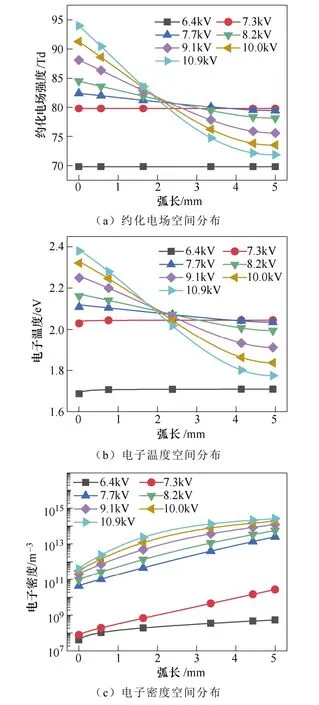
图7 施加电压对电场和电子温度及电子密度的 空间分布的影响Fig.7 The influence of voltage on the distribution of the electric field, electron temperature and electron density
当氨的浓度达到最大值时,反应器中的电场强度分布在79.4~82.4Td之间,电子温度分布在2.03~ 2.10eV之间,电子密度分布在4.3×1010~2.5×1013m-3之间。在上面所列的这些条件下,对于氨的合成来说是最有效的。
3.2 初始氮气和氢气比例对氨合成的影响
初始氮气和氢气比例对NH3数密度的影响如图8所示。从图8可以看出,随着N2∶H2比例的降低,氨气产量逐渐增加。当N2∶H2=1∶2时,氨气可获得最高产量,为4.2×1022m-3,随后氨气产量开始下降。J. Hong等[13]实验结果表明,当氢气比例为0.66时,氨气的产量达到最高,为2.2×1023m-3。尽管仿真与实验的反应条件设置上有所区别,但都是在N2:H2=1:2的时候获得最高的氨气产量,一定程度上验证了模型的有效性。
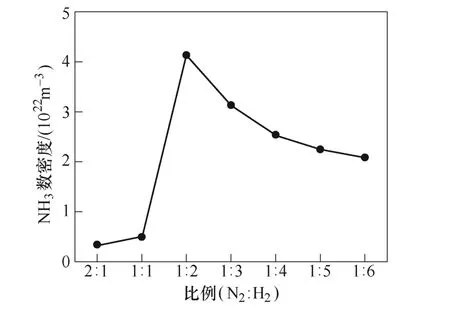
图8 初始氮气和氢气比例对NH3数密度的影响Fig.8 Concentration of NH3 as function of initial gas composition
图9为初始氮气与氢气比例对NH3产生和损失速率的影响。如图9a和图9b所示,NH3的产生速率逐渐增加且远大于图9c中的NH3的损失速率。这就导致了氨气产量的积累,当N2∶H2不满足化学计量比而是1∶2时,氨的产量最高。
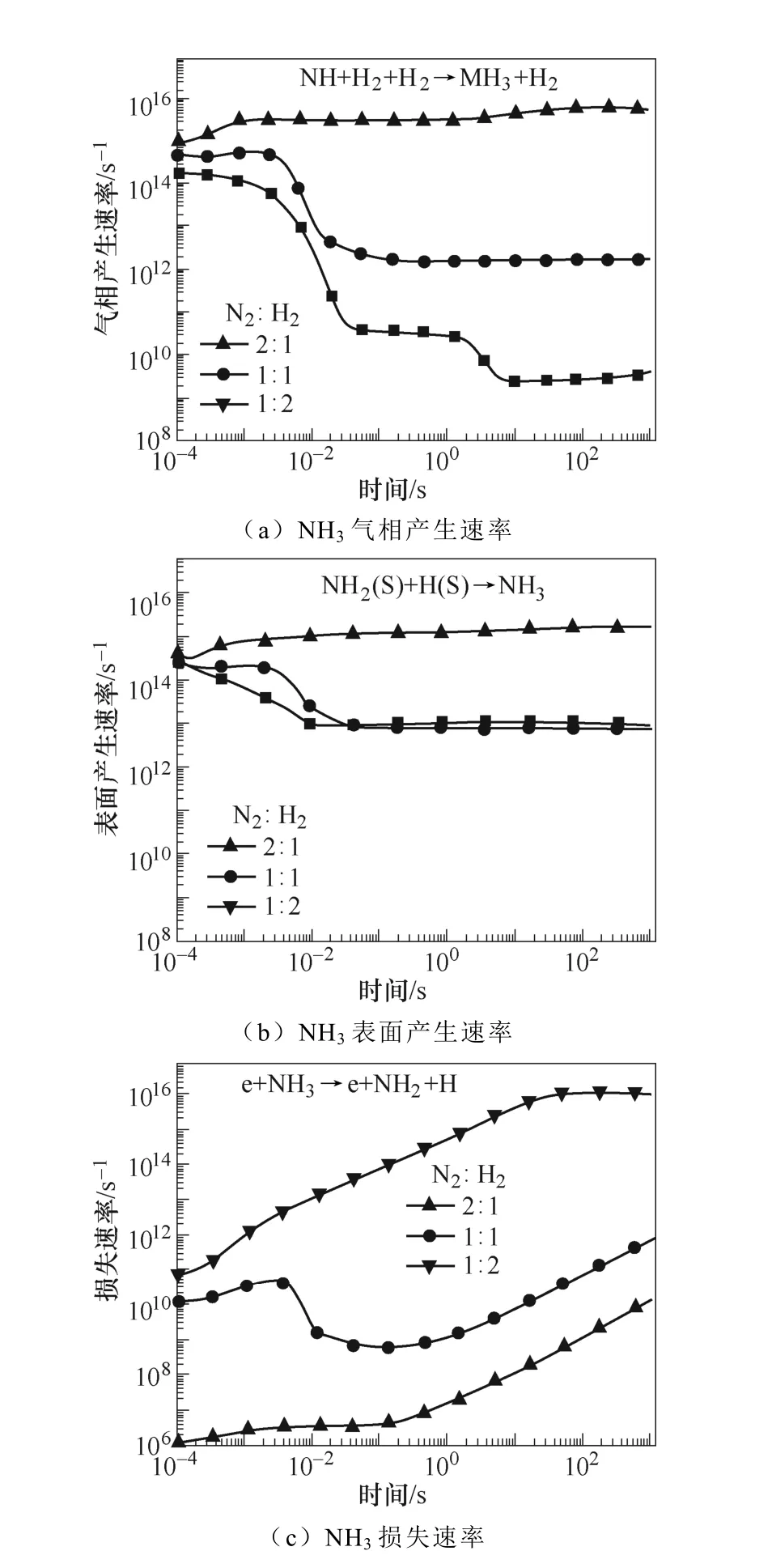
图9 初始氮气和氢气比例对NH3产生和 损失速率的影响Fig.9 The influence of initial ratio between N2 and H2 on the ammonia production and loss rate
图10展示了不同N2与H2比例下,不同电子碰撞反应过程中所消耗的电子能量的占比,包括N2和H2分子的电子激发、振动激发和电离。这项结果是通过BOLSIG+求解器计算得到。当N2∶H2的比例超过1∶2时,振动激发态的N2分子略有减少,振动激发态N2分子有助于关键粒子N(S)的形成,而N(S)的减少导致氨产量的降低。

图10 不同反应通道下的电子能量损失占比Fig.10 Electron energy loss fraction of different channels
图11显示了不同H2浓度下电子密度和电子温度的变化。初始H2的比例越高,空间分布中的电子密度越高。从图11b可以看出,当电子温度在2.0~ 2.17eV范围内,氨气浓度达到了最大值。这表明电子能量主要是用于N2分子的电子和振动激发,这有利于氨的合成。
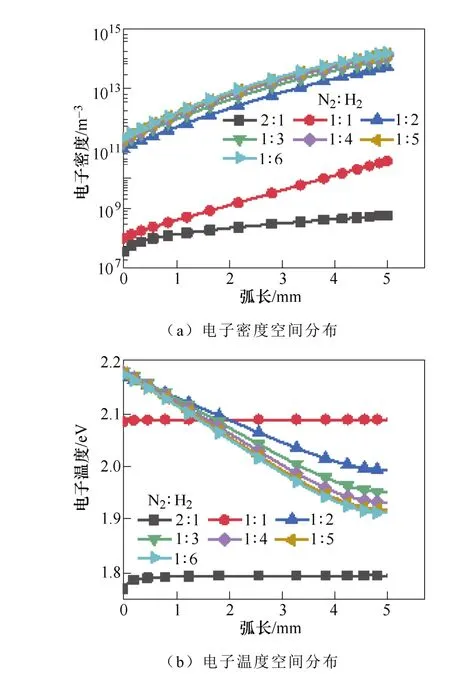
图11 初始氮气和氢气比例对电子密度和 电子温度的影响Fig.11 The influence of N2∶H2 ratio on electron density and electron temperature
3.3 催化剂材料表面总活性位点数对氨密度的影响
图12显示了催化剂表面总活性位点数目对NH3数密度的影响。以往的仿真中,总表面活性位点数采用一个固定值1015cm-2。在本文的一维模型中,假设催化反应发生在电极表面,且电极表面有限,而在真实等离子体反应器中,各粒子是在反应器空间内的催化剂表面发生化学反应,其表面积比平行板电极表面大得多,因此在这里讨论增大总表面活性位点数是有意义的。随着表面总活性位点数由1014cm-2增加到1018cm-2,氨气产量略有增加,增加幅度为9.89%。

图12 总表面活性位点数对NH3数密度的影响Fig.12 Concentration of NH3 as function of total free surface sites
这一结论似乎与催化剂表面有大量的自由活性位点,将极大地提高氨的产量的物理直觉不符。为了解释这种现象,进一步探究了反应过程中的不同表面粒子的数密度。不同总表面位点下表面粒子数密度的比较如图13所示,催化剂表面H(S)的密度比 N(S)的密度高了大约3个数量级。表面主要被H(S) 占据,限制了N(S)的吸附过程,这说明单纯增加总表面活性位点数对于氨气产量的提高是有限的。而采取其他方法增加表面吸附粒子N(S)的比例将有利于提高氨气的产量。

图13 不同总表面位点下表面粒子数密度的比较Fig.13 Comparison of surface-adsorbed species at different total surface sites
4 结论
本文建立了大气压下低温等离子体催化合成氨的一维流体动力学模型,研究了等离子体催化氨合成的物理机制。结论如下:
当电压增大到一定值时氨气产量反而下降,说明存在最佳反应电压条件。当N2/H2的比例不满足化学计量比,而是在1∶2时最有利于氨的合成。随着催化剂上自由位点密度增大4个数量级,氨气产量增加了9.89%。此外,该模型可以清晰地显示等离子体反应器中的电场强度、电子温度和电子密度的空间分布情况。当反应过程处在这些条件下,也就是电场的分布在79.4~82.4Td范围内,电子温度处在2.0~2.17eV之间,电子密度在4.3×1010~2.5× 1013m-3范围内,对氨的合成是最有效率的。
未来将进一步建立带有填充催化剂的DBD等离子体介质阻挡放电的二维模型,深入探究催化剂与等离子体相互作用对氨合成的影响。
