Spatial pattern dynamics among co-dominant populations in early secondary forests in Southwest China

Yuanfa Li·Minghui Li·Angang Ming·Hongxiang Wang·Sufang Yu·Shaoming Ye,2

Abstract The canopy of subtropical natural forests usually consists of several co-dominant populations (CDPs),which play a crucial role in forest structure,formation of the forest environment,and ecological function.However,little attention has been given to changes in spatial patterns in CDPs during natural succession.Cyclobalanopsis glauca (Thunb.)Oerst.,Quercus variabilis Blume,and Pinus yunnanensis var.tenuifolia W.C.Cheng &Y.W.Law are canopy species that form CDPs in zonal forests along the Nanpan River in southwest China.We used the g(r) function and its bivariate distribution model,g 12 (r),which is based on distances between pairs of points,to explore the dynamics of the three CDP species with respect to distribution patterns and spatial correlations in two secondary forests (one 30-year-old forest [30-YF] and one 57-year-old forest [57-YF]).The following key results were obtained:(1) there was a clumped pattern in the 30-YF,but the intensity of aggregation varied among populations and life stages.The distribution pattern gradually shifted to become random with longer succession time (i.e.,30-YF vs.57-YF),expansion of the observation scale (r =0–20 m),and at later life stages.(2) Aside from the mid-sized C.glauca trees and large P.yunnanensis trees,the trees repulsed each other at certain scales (r =0–2,5–6,11–12,14–16 m) in the 30-YF.Almost all of the life stages in the CDPs were independently correlated.This independent correlation was exacerbated by a longer succession time.(3) An increase in life stages and longer succession also promoted independent changes in intraspecific correlations.(4) Intraspecific correlations were stronger than interspecific correlations.Our results showed that reducing exclusive competition is essential to coexistence in CDPs.Inter-and intra-specific repulsion may occur at the same time,but intraspecific repulsion was the main driving force behind the random distributions and independent correlations.

Keywords Co-dominant populations·Competition·Secondary forest·Spatial correlations·Distribution patterns

Introduction

The patterns and processes underlying distribution are important components of the spatial dynamics of tree species in stable forests.These concepts have mostly been explored through the lenses of patch structure and natural disturbance (e.g.,competition,demographics,dispersal,mortality,and regeneration) (Getzin et al.2008;Li et al.2019),which,together,comprise patch dynamics (Eddy 1996).Distribution patterns have both spatial and temporal aspects (Schröder and Seppelt 2006).Processes are often difficult to directly observe and measure,but they influence several aspects of the forest ecosystem,including biomass,snag abundance and decomposition,carbon storage,species diversity,and neighborhood relationships,among others.Distribution patterns and processes interact with one another (Watt 1947;Schröder and Seppelt 2006;Forrester 2019);The distribution patterns can be thought of as the“footprints”left by processes,which then synthetically feedback via interactions among neighbors as well as adaptation and changes in tree species in response to abiotic conditions(Getzin et al.2008;Miao et al.2018;Omelko et al.2018).In other words,we can infer underlying processes by studying the characteristics of distribution patterns,to better understand natural phenomena and the complexity and long-term dynamics of forests (Cutler et al.2008).

The spatial distribution of plants can be assessed using mapped occurrences (Muvengwi et al.2018).In the last half century,analysis methods have been refined or replaced with updated methods.Spatial statistics,such as Ripley’s K function and improved models (e.g.,g(r),L(r)),have addressed some of the difficulties associated with scale-dependency while also effectively identifying interactions (i.e.,secondorder effects) using heterogeneity models or other tests rooted in ecological theory (Getzin et al.2008 ;Bagchi et al.2011;Wiegand and Moloney 2014;Nguyen et al.2018).Many studies of spatial patterns in forests (i.e.,distribution patterns and spatial correlations) have been conducted in tropical (e.g.,Condit et al.2000;Zhu et al.2015;Miao et al.2018;Muvengwi et al.2018;Nguyen et al.2018) and temperate regions (e.g.,Aldrich et al.2003;Getzin et al.2006,2008;Piao et al.2013;Omelko et al.2018 ;Liu et al.2020).Due to the short timeframe (＜ 35 years) since the establishment of most permanent fixed monitoring quadrats,and the slow rate of change in forest spatial patterns,such datasets consist of data from only one or a few time points.To date,very few studies have analyzed the spatial dynamics of tree populations over different successional stages using pointpattern analysis (Zhang et al.2012).

Natural forests are abundant in subtropical regions.Due to their proximity to large populations and human dependence on forest ecosystem services,most subtropical forests have been subjected to different types and intensities of human disturbance (e.g.,clear cutting,selective harvest,burning,pilfering,and grazing) over different timescales,after which forests regenerate naturally.This has resulted in an abundance of secondary forests that are managed under a variety of local government protection strategies,including closures to facilitate afforestation,returning farmland to forests,and rural migrants (Wang 1987;Li et al.2019).These secondary forests are now at the early stages of succession(Li et al.2019,2020).The canopy usually contains several co-dominant populations (CDPs),which have an obvious controlling effect on the forest structure and the surrounding environment.Together they comprise the skeleton and determine the appearance and type of forest (Li et al.2010).These CDPs are generally pioneer tree species,and differ greatly from non-pioneer tree species in various habitats(Clark et al.1993).Due to the limited availability of spatial data (Lin et al.2011;Bagchi et al.2011),few studies have examined the spatial patterns of tree populations in secondary forests,though some studies are available,for example,on evergreen broad-leaved forests (Li et al.2010;Zhu et al.2010;Luo et al.2012),mixed evergreen and deciduous forests (Guo et al.2015;Li et al.2017,2019),and deciduous broad-leaved forests (Li and Zhang 2015).However,there have been no previous studies on spatial patterns in CDPs over time in subtropical regions.

In the absence of long-term datasets,most studies of spatial patterns divided study populations into different life stages based on tree diameter,height,or age,and analyzed structural characteristics within these stages (e.g.,Hao et al.2007;Wang et al.2017;Muvengwi et al.2018;Omelko et al.2018).It is widely believed that competition,particularly intraspecific competition,is the main driver of differentiation in tree size,and it decreases individual abundance and aggregation intensity (Adler et al.2018;Pommerening and Meador 2018;Liu et al.2020).If negative density mortality occurs,the population will tend toward a regular distribution pattern (Getzin et al.2006;Lutz et al.2014;Muvengwi et al.2018).This trend has been observed in natural pure (e.g.,Kenkel 1988;Newton and Jolliffe 1998;Wang et al.2017)and mixed forests (e.g.,Getzin et al.2006;Luo et al.2012;Piao et al.2013,2014;Zhu et al.2010,2015) with uneven age distributions.Another way of assessing spatial patterns is to directly compare patterns in different-aged stands within the same forest type.This approach may contribute to a more detailed understanding of successional processes;however,such studies are rare in natural forests,perhaps largely because of insufficient sampling.We expect that with the increased age and a later life stage:(1) aggregation in CDPs will decrease;(2) intra-and inter-specific associations will weaken and become increasingly independent;and (3)intra-and inter-specific competition will both be present,but the role of intraspecific competition will be more significant due to the effect of similar niche requirements.We tested these hypotheses at the stand level using two standard fixed plots established in two stands of different ages in a zonal forest in the Nanpan River Basin in southwest China.

Materials and methods

Study site

Sampling was conducted in pine-oak mixed forests located at the Langquan and Yigou conservation stations in the Guangxi Yachang Orchid National Nature Reserve,Leye County,China (Fig.1).The two sites are in close proximity and share the same dominant vegetation types historically(Wang 1987).The Langquan forest originated from aPinus yunnanensisvar.tenuifoliaW.C.Cheng &Y.W.Law (hereafterP.yunnanensis) forest that burned in a wildfire in 1987(106° 19′ 4.2″ N,24° 51′ 15.9″ E).The Yigou site is also a secondary forest (106° 14′ 14.6″ N,24° 47′ 25.4″ E),but was formed from a clear-cut area of original forest during the era of“big steel”(1958–1960) (Li et al.2017,2019,2020).They represent the typical coniferous and broad-mixed secondary vegetation in the Nanpan River basin,with both being well-developed and having a high degree of naturalness.Overstory species composition was similar between sites and was dominated by the strongly shade-intolerantP.yunnanensisalong with two shade-tolerant species,Cyclobalanopsis glauca(Thunb.) Oerst.andQuercus variabilisBlume (Table 1,in dark grey).Other common species in both forests includeAlbizia kalkoraRoxb.) Prain,EuryadistichophyllaHemsl.,Keteleeria davidiana(Bertr.) Beissn.,Rhus chinensisMill.,Schima wallichii(DC.) Choisy,andWendlandia uvariifoliaHance (Table 1,in light grey).The Yigou forest may be considered a potential successional endpoint of the Langquan forest.More information about pine-oak mixed forests in the region can be found in Li et al.(2017,2019,2020).

Plot establishment

In 2016–2017,we established square plots (100 m × 100 m in the 30-year-old forest [30-YF];80 m × 80 m in the 57-year-old forest [57-YF]) at the two conservation stations(Fig.1 a and b).First,a target forest stand was identified using a typical sampling method,and then a total station instrument (model NTS-372R10;Southern Mapping Company) was used to locate the first boundary of the sample along the horizontal slope.The remaining three sides were then measured clockwise,and the closure difference was controlled to within 1/200.Each plot was then divided into several 20 m × 20 m sub-plots,and three-dimensional coordinates (x,y,z) were collected for each tree using the total station instrument.Plastic tubes (ø=6 cm) were fixed at each intersection to mark sub-plots.Each tree with a diameter at breast height (DBH) ≥ 5 cm was tagged.Species name,health status,and regeneration status were recorded,and the DBH,height,and crown diameter were assessed for each tree or shrub.A total of 2391 live individuals,comprising 16 tree species and two shrub species,were detected in the 30-YF.In the 57-YF,we documented 1019 live individuals from 13 tree species and four shrub species.Combined,C.glauca,Q.variabilis,andP.yunnanensisaccounted for 49.0% and 67.5% of the abundance as well as 73.2% and 87.4% of the basal area in both forest stands,and thus merit CDP status (Table 1).

Fig.1 Pine-oak mixed forests are the zonal vegetation along Nanpan river China PR.Our forest stands are located at the up slope of two huge mountains situated at Langquan and Yigou conservation stations,Leye,Guangxi (top row).The point patterns of the CDPs C.glauca,Q.variabilis and P.yunnanensis are marked by solid circle,hollow triangle and annulus,respectively.The residuals tree species are represented by the grey dots.The background colors represent the intensity of points and the white lines are contours

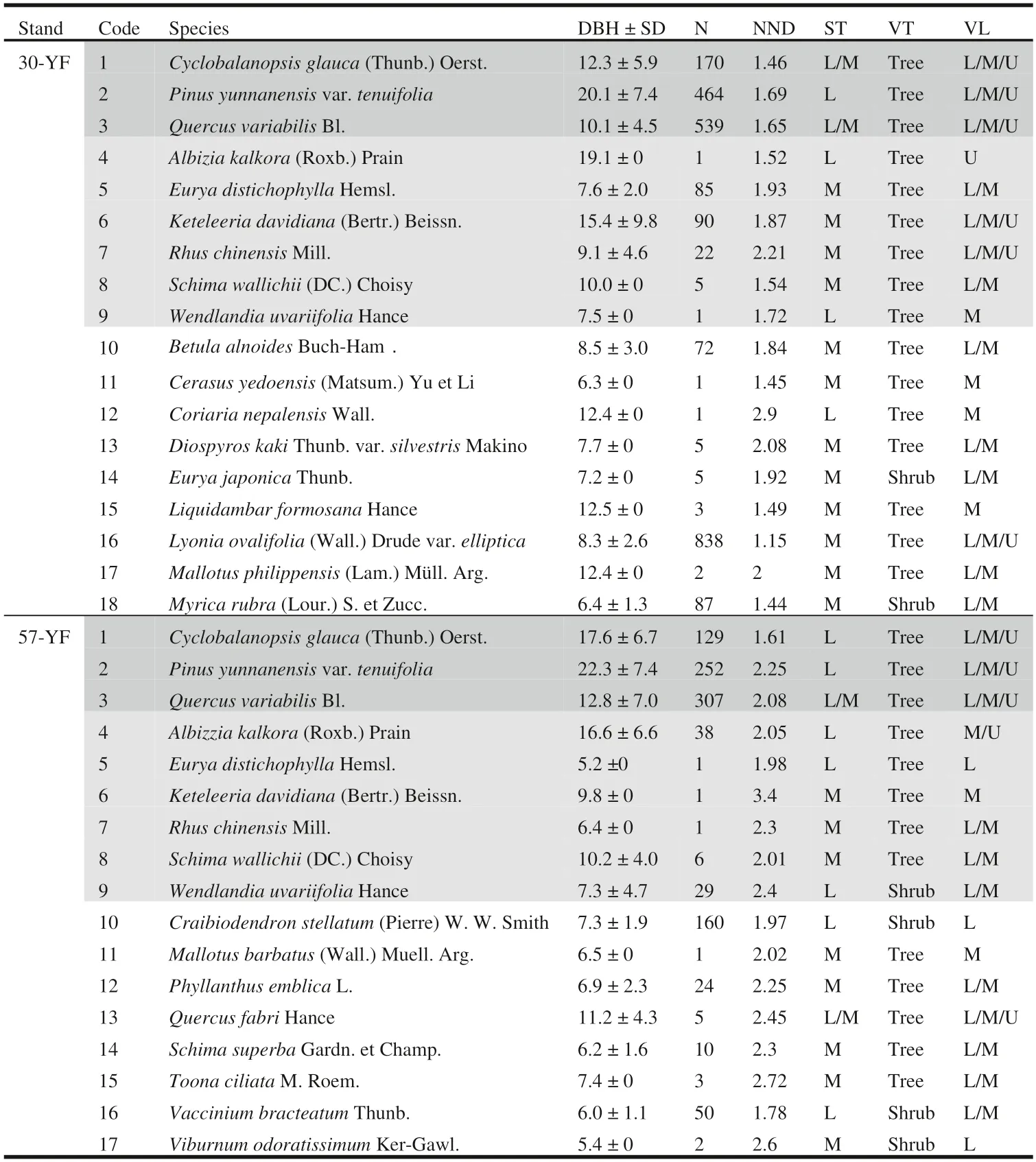
Table 1 Quantitative characteristics of populations in pine-oak mixed forest along the Nanpan River,P.R.China

Spatial pattern analysis

Changes in spatial pattern with scale are an important feature of a natural forest.Ripley’sK(r) function (Eq.1),which is based on the distance between a pair of points,calculates the number of trees in a certain circular area based on a reference tree (Zhu et al.2010;Wiegand and Moloney 2014).The square of theK(r) function is theL(r) function (Eq.2).TheL(r) function is not sensitive to the distribution pattern changes caused by adjacent trees at small scales,and is therefore highly suitable for the detection of heterogeneity in habitats.Another improvement toK(r) functions is the pair correlation function (Eq.3),which substitutes the circle used inK(r) function analysis with a ring,eliminates the cumulative effect,is highly sensitive to changes in distribution pattern at small scales,and is more intuitive (Getzin et al.2006;Wiegand and Moloney 2014;Li et al.2019).The univariate distribution model,g(r),is suitable for the analysis of distribution patterns,while the bivariate distribution model,g12(r),is suitable for the analysis of inter-and intraspecific correlations (Getzin et al.2006,2008;Wiegand and Moloney 2014;Li et al.2019).The distribution pattern of,and spatial correlation among trees are determined by comparing the observed values to expected values under a Poisson distribution;g(r)=1 suggests a random distribution,whileg(r) ＞ 1 implies an aggregated distribution.The distribution pattern is regular ifg(r) ＜ 1.Similarly,there are no correlations among or within species ifg12(r)=1.Ifg12(r) ≥ 1,there is an inter-or intra-specific attraction,whereasg12(r) ＜ 1 indicates inter-or intra-specific repulsion (Getzin et al.2006,2008;Lutz et al.2014;Nguyen et al.2018).

whereA=area;N=number of trees;r=the observation scale (0,1,2… 20 m);λ=density;andw ijis the weight.

Statistical analyses

Habitat heterogeneity (i.e.,a first-order effect) influences the interactions between neighbors (Getzin et al.2008;Zhu et al.2010).It is generally believed that the growth of large trees is determined less by neighboring trees than by the spatial heterogeneity of the habitat (e.g.,water,topography,and nutrition).Some studies use large trees to test whether the stand is heterogeneous (e.g.,Piao et al.2013;Wiegand and Moloney 2014;Li et al.2019).In this study,we assumed that no heterogeneity existed in each stand,i.e.,that the distribution pattern of the large trees (DBH ≥ 25 cm) satisfied the Poisson homogeneity test.We usedg(r) andL(r) to analyze the distribution pattern of large trees,at relatively large scales of up to 40 m,based on the null model of complete spatial randomness (CSR).It was found that all the observed values of the two methods fell into the upper and lower 95%confidence intervals of a Monte Carlo test,indicating no clear habitat heterogeneity in the stands (Appendix Fig.S1).Therefore,any influence of heterogeneity on the spatial patterns of the tree populations was discounted.

We then divided trees in each population into three groups with DBH:5–15 cm (small),15–25 cm (medium),and ＞ 25 cm (large),representing three life stages,i.e.,juvenile,mature,and old-growth.At both sites,Q.variabilisandC.glaucapopulations were represented by two life stages,whereas theP.yunnanensispopulation was represented by all three stages.Only populations/life stages comprising ≥ 30 individuals were included in the analysis.Considering stand age and tree size,we analyzed the distribution patterns of the three populations and their life stages at a scale of one quarter of the distance of the short edge of the quadrat(r=0–20 m),usingg(r) based on the null model.Twelve pairs of interspecific correlations and 28 pairs of interspecific correlations were analyzed at different life stages usingg12(r) based on a null model of the independence of components,and 10 pairs of intraspecific correlations were analyzed usingg12(r) based on a null model of random labeling.The Monte Carlo method was used to simulate the observed values 199 times at each scale,and the maximum 2.5% and minimum 2.5% of the values of the simulated dataset were used to draw the envelope.Significance was determined by a two-sided test and the edge correction of the plots was used to choose the best model.To avoid Type I error inflation,we used a goodness-of-fit test to evaluate the significance of the observed patterns (Wiegand and Moloney 2014;Baddeley et al.2015).Observed values falling outside the envelope suggested significant differences;otherwise,the distribution was assumed to be random,i.e.,no significant relationship.Analyses were conducted using the“spatstat”package (Baddeley et al.2015) in R (R Core Team 2019).

Results

Distribution patterns in the CDPs

At all observation scales,theC.glaucapopulation and its small-and medium-sized trees showed complete deviation from the 95% Monte Carlo simulation interval in the 30-YF,and were in an aggregated state (Fig.2 a).Although they were strongly aggregated at very small scales (r=0–2 m)in the 57-YF,they approached or showed a random distribution at the other scales (r=3–20 m) (Fig.2 d).The same trend was also apparent in theQ.variabilisandP.yunnanensispopulations,i.e.,their distribution pattern in the 30-YF was more clustered than in the 57-YF,but the difference was minor.Among them,theQ.variabilispopulation had a random pattern only at a small scale (r=2–3,and 7–8 m)in the 30-YF (Fig.2 b),while it had a random pattern at most scales (r=0–1,and 8–20 m) in the 57-YF (Fig.2 e).The small-sized trees ofQ.variabiliswere almost all clustered in the 30-YF (Fig.2 b),but they became random whenr≥ 8 m in the 57-YF (Fig.2 e).The distribution pattern of the medium-sizedQ.variabiliswas also transformed into a random distribution asr=0–17 m becamer=0–20 m,with an increase in forest age (Fig.2 b and e).TheP.yunnanensispopulation and its small-and medium-sized trees deviated from a random distribution at all scales (r=0–20 m) in the 30-YF (Fig.2 c),but in the 57-YF,only the population deviated slightly from a random distribution at a few scales(r=8–9 m),while its small-,medium-and large-sized trees were randomly distributed at all scales (Fig.2 f).

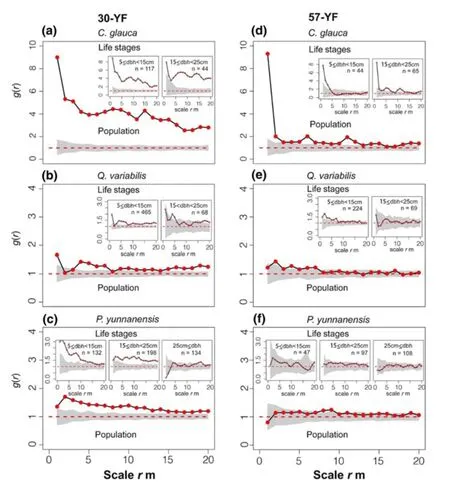
Fig.2 Distribution patterns of the three co-dominant populations and their life stages based on the null model of complete spatial randomness.In each plot,the red dashed line stands for the value of expectation under Poisson distribution,the solid black line with red circles represents observed value and the grey area dominates 95% Monte Carlo simulation envelope.n is the number of individuals

Interspecific correlations in the CDPs

In the 30-YF,the spatial correlations betweenQ.variabilisandC.glauca,andQ.variabilisandP.yunnanensis,were independent at each scale (Fig.3 a,b,e,f);these relationships were similar in the 57-YF (Fig.3 g,h,k,l).Spatial correlations betweenP.yunnanensisandC.glaucavaried between repulsion and independence.They repulsed each other atr=0–2,7–14,4–8 and 11–12 m,but were independent atr=2–7,14–20,0–4,8–11 and 12–20 m in the 30-YF(Fig.3 c and d).By contrast,they were independently correlated at all scales (r=0–20 m) in the 57-YF (Fig.3 i and j).The spatial horizontal relationships of the point patterns of any two populations also directly reflected their spatial correlation (Fig.1 a and b).

Fig.3 Spatial correlations of the three co-dominant populations based on the null model of the independence of components.The g12(r) and g21(r) functions are simultaneously used to detect the spatial correlations which show a close similarity.The red dashed lines represent the value of expectation under Poisson distribution,the solid black lines with red circles represent observed values and the grey areas dominate 95% Monte Carlo simulation envelope

Interspecific correlations in the CDPs at different life stages

Aside from a slight exclusion of small individuals ofC.glaucaand small and medium individuals ofQ.variabilisin the 57-YF (Fig.4 e1 and f1),there were no correlations among life stages ofC.glaucaandQ.variabilis(Fig.4 al–d1,g1,h1).In the 30-YF,the medium-sizedC.glaucaand largesizedP.yunnanensisrepulsed each other atr=0–2,5–6,11–12,and 14–16 m (Fig.4 f2),while most of the residual life stages were independently correlated (Fig.4 a2–e2).Spatial correlations among life stages ofC.glaucaandP.yunnanensisbecame completely independent as forest age increased (Fig.4 g2–l2).Aside from a select few scales,the different life stages ofQ.variabilisandP.yunnanensishad almost no correlations with each other (Fig.4 a3–l3).

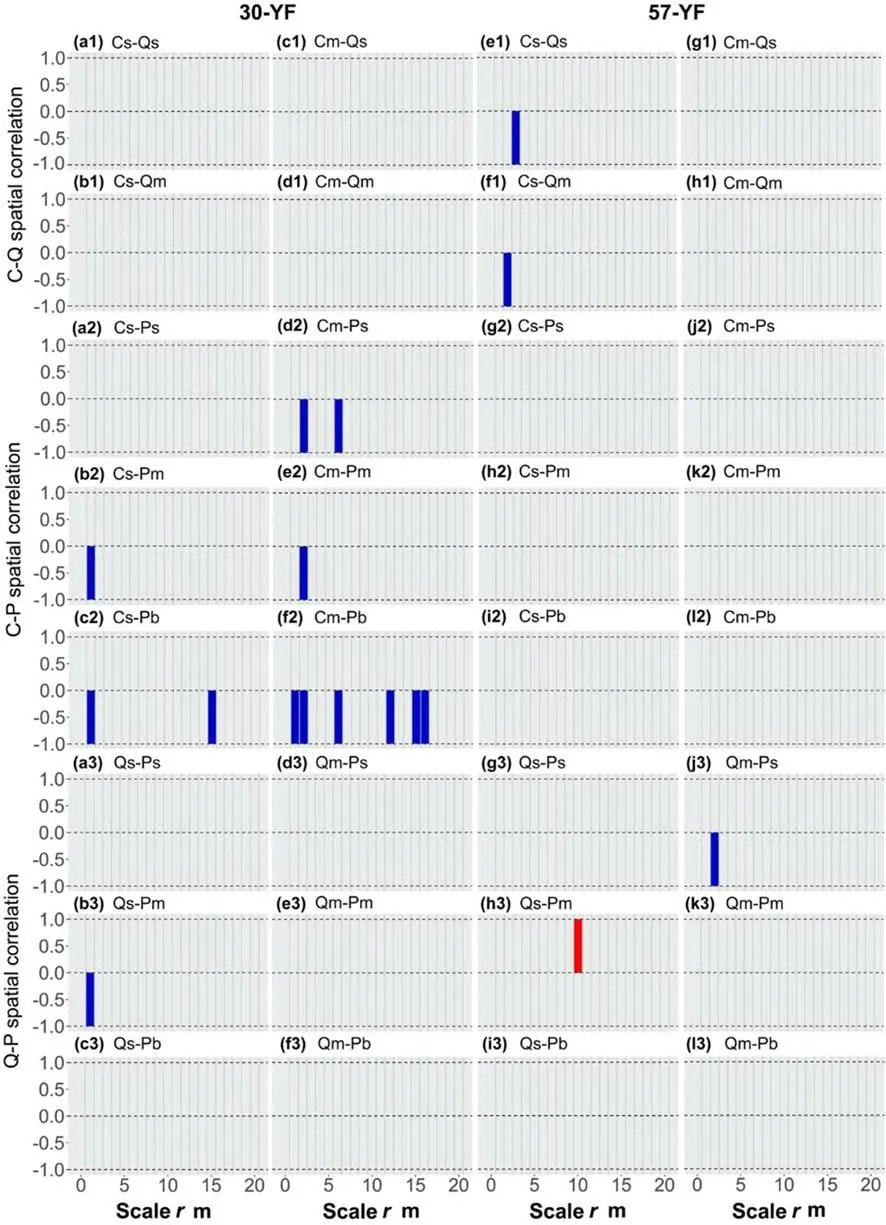
Fig.4 Interspecific correlation of the three co-dominant populations at different life stages based on the null model of the independence of components.The sub-graphs show tree species by size:capital letters represent tree species and lower case letters denote tree sizes.The letters s,m,and b indicate small-,medium-,and large-sized trees,while P,Q and C represented P.yunnannesis,Q.variabilis and C.glauca population,respectively.The colored stripes indicate spatial correlations between a pair of populations in a given life stage.The blue,gray,and red colors indicate repulsion,randomness,and attraction,respectively

Intraspecific correlations in the CDPs at different life stages

In the 30-YF,small-and medium-sizedC.glaucaandP.yunnanensisdisplayed a mutual attraction at most scales(r=0–19 m andr=0–12,14–16 m,respectively) (Fig.5 a and c),but the degree of attraction in the 57-YF was significantly lower,only occurring on the scales ofr=0–2,4–6,and 19–20 m,andr=8–10,14–15,and 19–20 m,respectively (Fig.5 fand h).The small-and large-sizedP.yunnanensiswere mutually repulsed at a few scales (r=8–9,14–16 m),while they were independent at the residual scales in the 30-YF (Fig.5 d).These independent relationships were seen at all scales in the 57-YF (Fig.5 i).The relationship between medium and largeP.yunnanensiswas almost independent in both stands (Figs.5 e and j).In the 30-YF,the small and mediumQ.variabilisrepelled each other on small scales (r=2–3,11–12 and 13–14 m),while they were an independently correlated at most of the other scales(Fig.5 b).Except for attraction at the scale ofr=18–19 m,they also displayed an independent correlation at most scales in the 57-YF (Fig.5 g).

Fig.5 Interspecific correlation of the three co-dominant populations at different life stages based on the null model of random labeling.The colored stripes indicate spatial correlations between a pair of populations in a given life stage.The blue,gray,and red colors indicate repulsion,randomness,and attraction,respectively

Discussion

Spatial dynamics in CDPs

After controlling for habitat heterogeneity (Appendix Fig.S1),we found that the distribution patterns in the CDPs shifted from aggregated to random with increasing age in pine-oak mixed forests (Fig.2 a–f).One possible explanation for this is that a large number of cones,large seeds,and stumps in the CDPs were left behind after harvesting and burning resulted the complete destruction of the original forests.Shade-intolerant species subsequently established in these areas,resulting in a clustered pattern (Li et al.2019).The spatial requirements of trees increase as they grow larger,resulting in heightened competition among neighbors,which in turn leads to decreased growth or death,ultimately leading to decreased aggregation at the stand scale (Getzin et al.2006;Li et al.2012;Bieng et al.2013;Miao et al.2018;Pommerening and Meador 2018).The relationship between intraspecific life stages and distribution patterns has been widely reported in oak forests (e.g.,Wang et al.2014;Piao et al.2014;Petritan et al.2014;Li et al.2019),other natural forest types (e.g.,Ward et al.1996;Condit et al.2000;Boyden et al.2005;Lin and Augspurger 2008;Zhu et al.2010;Torimaru et al.2013;Omelko et al.2018),and in vertical forest stratifications (e.g.,Hoshino et al.2001;Hao et al.2007;Getzin et al.2011;Li et al.2019);this relationship is considered a basic rule in population dynamics.Another explanatory mechanism for aggregated distribution patterns is that some individuals ofC.glaucaandQ.variabilishad reached physiological maturity and were producing seeds (Li et al.2019),thus promoting highly aggregated groups of seedlings;conversely,P.yunnanensisdoes not regenerate or grow well under dense canopy cover.We did not find any regeneration or saplings (DBH ＜ 5 cm) in the 30-YF and found only a few recruits in large gaps in the 57-YF.Some studies have reported that conifers and hardwoods in pine-oak mixed forests adopt different strategies for regeneration and growth (Hao et al.2007),which may promote long-term coexistence in CDPs and contribute to the patterns we observed.

Spatial dynamics in the CDPs in forest stands

Forest age substantially influences the spatial distribution in stands (Li et al.2107).Tree number and aggregation in the CDPs decreased at later successional stages (Fig.2 a–f),which highlights the importance of process and indicates that clump mortality caused by asymmetric competition is likely to occur at all life stages (Franklin et al.1987;Hurst et al.2012;Pommerening and Meador 2018).This phenomenon has been widely documented in other forests,particularly those at early successional stages (Lutz and Halpern,2006;Wang et al.2017),and among young and small trees in older forests (e.g.,Kubota et al.2007;Lin and Augspurger 2008;Piao et al.2013).When the same species are present as pioneer species,they are more likely to have a higher mortality rate due to self-thinning (He and Duncan 2000).Moreover,the time required to form random distribution patterns in CDPs can differ (Fig.2).This may be related to environmental conditions (e.g.,light,nutrition,and water),the developmental stage,or biological characteristics (Watt 1947;Kubota et al.2007;Nguyen et al.2018).Some studies have noted that the formation of random patterns in tree populations is a long process,and some populations cannot ultimately deviate from an aggregation state to assume a regular distribution at a small scale (Getzin et al.2006;Omelko et al.2018).Changes in the distribution patterns in the CDPs at our study sites were thus consistent with the results of long-term monitoring of other forests (e.g.,Ward et al.1996;Aldrich et al.2003).

Dynamics of interspecific correlations

Spatial correlations betweenQ.variabilisand populations of the other two species (Fig.3 a–b,e–f,g–h,k–l),and across life stages (Fig.4 a1–h1,a3–l3),indicate that independence occurred early (＜ 30 years) and persisted thereafter.This relationship is likely attributable to the life characteristics,spatial distribution,and morphology of the three species.Cyclobalanopsis glaucais an evergreen,whereasQ.variabilisis a deciduous broadleaf species;this distinction may reduce direct competition between the two species.In addition,theC.glaucapopulation in the 30-YF was mainly concentrated in up-slope areas (Fig.1 a),and trees in the 57-YF mostly regenerated from stumps (Fig.1 b),whereas theQ.variabilispopulation was more evenly distributed across both stands (Fig.1 a and b).This spatial isolation may serve to further reduce competition (Li et al.2019).Pinus yunnanensisandQ.variabilisalso differ in their life characteristics;furthermore,the former has a narrower crown and grows taller.These differences in morphology,growth rate,and light dependence serve to eliminate competitive interactions between the two species (Li et al.2019).By contrast,C.glaucaandP.yunnanensisrepelled each other slightly in the 30-YF (Fig.3 c and d),but their spatial correlations were independent in the 57-YF (Fig.4 f2 vs.l2),suggesting that spatial correlations between these species are affected by the developmental stage (Condit et al.2000).Early CDPs in Korean pine mixed forests and pine-oak mixed forests in the Qinling Mountains exhibited similar competitive behaviors(Zhang et al.2015;Kang et al.2017).It is believed that independent correlations strongly dominate interspecific relationships in certain subtropical and tropical natural forests;this is further supported by the unified neutral theory(Nguyen et al.2018).

Dynamics of intraspecific correlations

Intraspecific correlations tend to become increasingly independent as succession advances (Fig.5).They are also more variable than interspecific correlations (hypothesis 3),as is consistent with their distribution patterns.Numerous studies of different forests suggest that the negative density effect is an important driver of intraspecific distributions and associations (e.g.,Getzin et al.2008;Bagchi et al.2011;Zhu et al.2010,2015;Luo et al.2012;Piao et al.2013,2014;Petritan et al.2014).This effect may also occur among the life stages ofP.yunnanensis(Fig.5 c–e,h–j),but other studies have suggested that the autotoxicity of pine may result in intraspecific repulsion (Fernandez et al.2008;Li et al.2019).We only observed one interspecific correlation,betweenC.glaucaandQ.variabilis,and it is impossible to determine whether or not a negative density effect was present;with the increase of forest age,however,spatial correlations between populations and among life stages shifted to become independent (Figs.3 and 5),implying the occurrence of intraspecific competition.A recent meta-analysis reported that 67% of terrestrial plants experience intra-and intra-specific competition (Adler et al.2018);intraspecific competition was found to be 4–5 times stronger than interspecific competition,and it promotes the stable coexistence of species at local scales (Adler et al.2018).Zhang et al.(1999) drew similar conclusions based on succession in several zonal forests,and further noted that the intra-and inter-specific relationships in CDPs were independent,with most CDPs having a very weak influence on one another.These studies generally agree with our results.

Conclusion

In the absence of obvious human interference and habitat heterogeneity,interactions between neighboring trees may play a central role in the successional process in CDPs.Most studies of CDPs have analyzed spatial patterns by combining datasets obtained from a single plot at one time with theoretical conjectures regarding the ecological processes controlling past succession.Here,we used a space-for-time approach to explore the dynamics of the spatial patterns ofC.glauca,Q.variabilis,andP.yunnanensisacross different life stages in the oak-pine mixed forests in the Nanpan River Basin.We found that distribution patterns and spatial correlations in CDPs became increasingly random and independent with increasing life stage,but the effects varied among populations.We also found that forest age had a significant effect on the number of individuals,distribution patterns,and inter-and intra-specific correlations in CDPs.In other words,with increasing age,the number of individuals within any given diameter class decreases,distribution patterns become increasingly random,and spatial correlations become increasingly independent.These trends suggest that a reduction in competitive exclusion promotes coexistence in CDPs.However,inter-and intra-specific competition may be present and promote the formation of stable spatial patterns in CDPs in the early stages of succession.Intraspecific competition,however,is stronger than interspecific competition,and was the main driver in the development of the CDPs.Our findings contribute to a better understanding of the structural status of forest stands and the mechanisms underlying species coexistence for the conservation of subtropical forests.

AcknowledgementsWe thank Guangxi Yachang National Orchids Natural Reserve Bureau and Guangxi Yachang State-owned Forest Farm for providing comprehensive field services.