岩质水工边坡力学参数概率分布研究及可靠度分析

潘海军，蒋强强

(安庆市水利水电规划设计院，安徽 安庆 246000)

1 工程概况

某水库是以防洪为主的综合利用水利枢纽，位于安徽省太湖县境内。根据大坝建设需求，需对右岸(坝)的边坡进行开挖处理，由于右岸存在断层F1，其岩性为炭质页岩结构较散，同时F1上部岩体受到断层影响，岩体风化严重使得岩体稳定性较差，因此开挖后的边坡稳定性极为重要；根据经验选取右岸边坡中一个典型剖面进行计算分析，见图1。

地质勘测表明该区域主要存在三种不同岩体以及断层F1，但由于长期的地质活动以及自然环境的影响，各岩体的力学性质变得非常复杂；如此使得各岩体的力学参数具有一定的不确定性，如表1所示各岩石力学性质并不是唯一确定值。

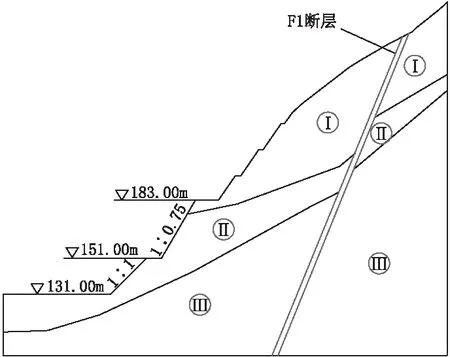
图1 开挖边坡剖面图

表1 岩石力学参数

对于边坡的稳定性分析，这些不确定性对分析结果存在巨大的影响，从而影响边坡安全；故在分析边坡稳定性前，需对不同岩体的各种特征参数进行研究。

2 计算参数及原理

2.1 岩石参数研究

根据数理统计理论以及地勘采样试验实际出发，对于岩石参数试验数据样本数量n可分为：小样本情况(n<30)、较大样本情况(3050)。对于小样本情况，目前多采用曲线拟合法、有限比较法、Bayes法等；较大样本与大样本情况所服从的概率模型分布，首先假定样本服从某一概率分布，然后采用K-S或χ2检验其是否服从假定的模型[1]。

根据地勘的岩石力学参数试验提供的样本数量n<30，为小样本情况，故采用曲线拟合法。从文献[2]可知，岩石的各力学参数近似服从于正态分布。根据地勘采样试验得到的样本，采用正态分布拟合[3]得到各岩石参数统计模型见表2。

表2 岩石力学参数概率模型

根据文献[4]中的研究可知，容重r、弹模E、泊松比v的变异性对边坡安全系数影响较小，故计算时考虑粘聚力c、内摩擦角φ的变异性影响，计算分析时对虑粘聚力c、内摩擦角φ按照其概率密度函数随机抽样，并进行正交数值实验分析。计算流程如下：(1)随机抽取n个粘聚力c的值为样本序列c[n]，以及n个内摩擦角φ的值为样本序列φ[n]；(2)依次在以上两个样本序列中选取ci与φi作为一组计算参数，并进行边坡稳定性分析；(3)重复步骤(2)，直至所有样本抽取完毕。上述过程中坡稳定性分析采用有限元强度折减法来计算。

2.2 基于强度折减法的边坡可靠度计算方法

(1)有限元强度折减法

计算边坡安全系数的强度折减法[5]，是在计算过程中不断折减抗剪强度参数(c、φ)，使其强度逐渐降低直至破坏，此时的折减系数即为安全系数F，表达式为：

(1)

式中：cf、φf分别为临界破坏时的粘聚力与内摩擦角。计算分析可采用ABAQUS软件，通常判别边坡失稳破坏的方法有三种：①边坡顶点位移突变；②强度折减区域出现塑性贯通区；③有限元迭代计算不收敛。鉴于塑性贯通区为边坡失稳的必要但非充分条件，迭代计算不收敛也受到求解参数设置的影响，故选用边坡顶点位移突变作为失稳判据。

(2)边坡结构可靠度计算方法[6]

可靠性是指在规定的时间内，结构在特定的工作条件下完成预定功能的能力。由于边坡岩石参数具有不确定性，故边坡的稳定性也是不确定的，因此计算边坡稳定时需考虑边坡可靠度。

对于c、φ为随机变量时可建立以下功能函数Z=g(c，φ)表示结构的状态：

Z=g(c，φ)=F(c，φ)-1

(2)

当Z>0时边坡为可靠状态，Z<0时边坡为失效状态，Z=0时为临界状态。假定Z服从正态分布，则可以得到边坡失效概率为：

(3)

其中，fz(z)为Z的概率密度函数：

(4)

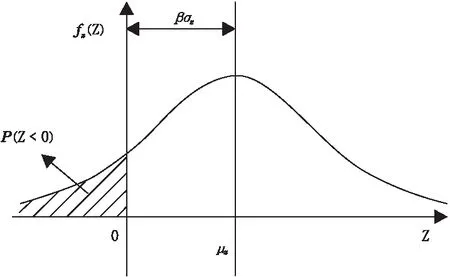
图2 失效概率与可靠度关系

可以用σz标准差度量原点O到均值μz的距离，定义有β=μz/σz，β则称为结构可靠度指标。

3 边坡稳定性分析

(1)计算模型

根据边坡剖面图，在ABAQUS中建立有限元模型，采用M-C模型进行随机抽样强度折减分析。分析时仅考虑自重荷载；对各材料的c、φ按照表2取其概率为0.2、0.4、0.6、0.8、1.0时对应的值(例如：当概率为0.2时，即表2中c对应的概率密度函数值为0.2；可以通过查寻正态分布表得到密度函数中x的值，即c的概率为0.2时c的值)进行正交数值实验组合分析边坡安全系数；其他材料属性采用均值。上述抽样中c、φ的值各5个，正交分析取二者的值两两组合，共5×5=25个样本，根据式(1)对材料参数进行强度折减，通过有限元计算得到每个样本的安全系数Fi。采用式(2)得到各样本的Zi，形成Zi的样本序列Z[25]；再根据式(3)、式(4)计算处理得到fz(z)。有限元模型见图3，沿X方向取380 m，Y方向200 m；模型一共2071个CPE4R单元，2142个节点；底面约束Y方向，两侧约束X方向；以断层外露顶点作为参考点。

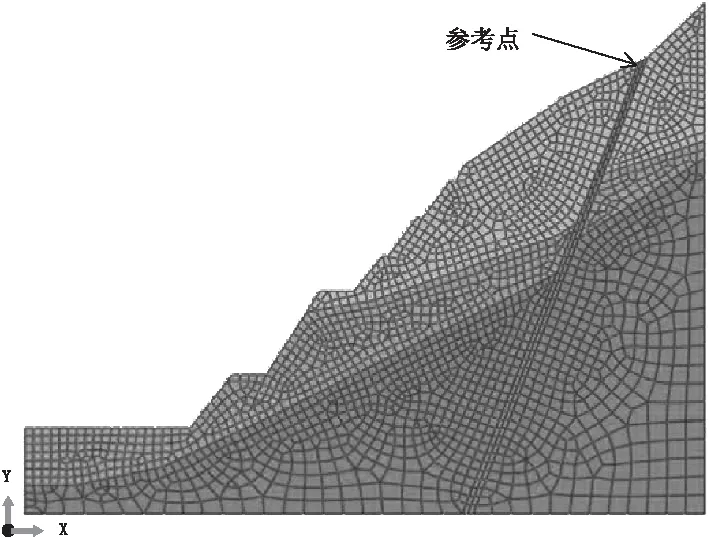
图3 边坡有限元模型

(2)结算结果及分析

计算中按照取c、φ正交实验组合值进行随机取样计算，计算25种情况下的安全系数，选取断层外露顶点作为参考点，得到不同c、φ值下的安全系数与位移关系，位移突变处(位移绝对值突然增大)即为安全系数；同时由计算模型可知在强度折减的过程中边坡会向左下方滑动失稳，故根据计算模型中所示的坐标系，水平位移向左为负值，竖向位移为负值，计算结果见图4。

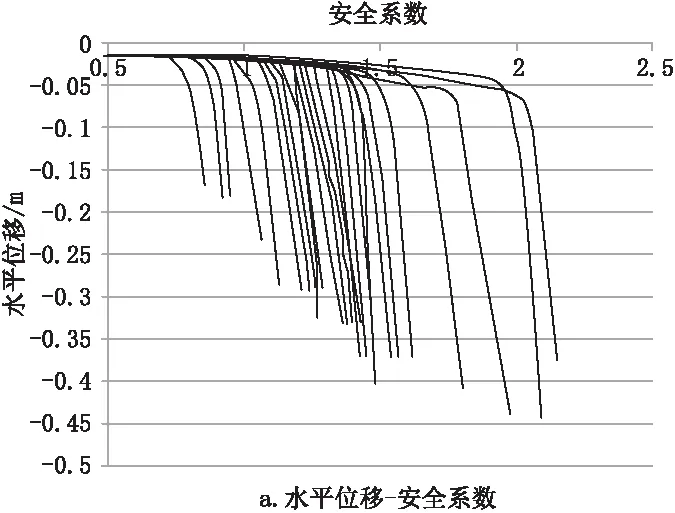
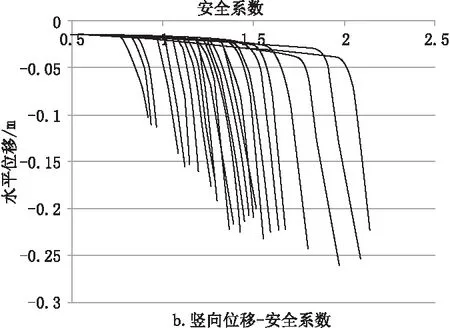
图4 参考点位移与安全系数关系

计算得到安全系数在0.63～2.05之间，从图中可以看出，安全系数密度在0.5～1.0之间较小，1.0～1.5之间较大，1.5～2.5也较小。根据得到的Fi序列(安全系数序列)按照式(2)计算得到Zi，对Zi序列进行分区处理，并计算Zi序列各区域的概率分布，见表3。

表3 Zi序列概率

对Zi进行正态分布拟合得到：

(5)

fz(z)的概率分布见图5。

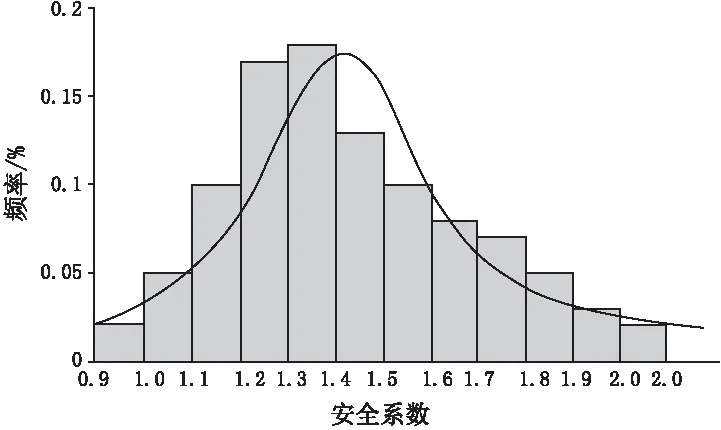
图5 安全系数概率分布

根据fz(z)可知安全系数期望值为1.28根据概率统计理论可用Φ(-β)≈P(z<1)查寻正太分布表求得可靠度β=1.84。

4 结论

通过对岩石参数进行正态拟合，得到了c、φ的概率密度函数，将其考虑成随机变量，通过正交实验得到了期望安全系数以及边坡可靠度，可得到以下结论：

(1)对于地勘提供的岩石力学实验参数，采用正态拟合简便可行，能够较准确的得到计算参数；

(2)利用ABAQUS对边坡进行强度折减分析，并对c、φ进行正交实验，能够更为准确的得到边坡安全系数以及可靠度，增加了计算结果的可信度；

(3)文中提出的边坡稳定性分析方法简便可行，可为后期边坡加固提供参考，也可为类似工程提供借鉴。