基于遗传算法的城市雨水排水管网改造优化

郑旭强

(重庆市勘测院，重庆 401123)

1 引言

城市排水网络能在雨季中引导城市雨水排出，并在一定程度上防止城市洪水事件[1]。这种网络的级别由其返回周期决定，网络的设计回报期越高，有形(经济)和无形(主要是社会方面)的损失就会越少，但同时会导致更大的投资[2]。许多国家雨水排放网络存在不能满足现状排水的需求，气候变化是其主要原因[3]。虽然气候变化在许多地区的影响是导致全年降雨量减少，但同时降雨强度也明显增加，无法及时排水将导致洪水问题发生。

在气候变化的背景下，现有的一些技术可以解决或减轻城市过度积水的问题。传统方法是通过增加全部或部分网络的容量来解决的。本文提出了另一种解决方案，即将管道改造与可持续城市排水系统技术相结合。具体地说，这项工作的重点是在部分改造排水管网和安装蓄水池的基础上，制定一套全面的雨水排水管网修复方法。本文采用了多目标遗传模型NSGA-II[4]，基于整个网络的水力要素进行建模，将城市排水优化视为一个多目标问题[5]，将水力分析与优化模型相结合，从而获得不同最优解的帕累托前沿，以实现减少项目最终预算为目的。

2 研究区概况

沙坪坝区位于重庆市主城区的西部，东隔嘉陵江与渝北区、江北区相望，南接九龙坡区，东南紧邻渝中区，北与北碚区相连，西依缙云山与壁山区毗邻。占重庆市总面积的0.48%，约为395.8 km2。沙坪坝区最南端在歌乐山镇山洞村，位于北纬29°27′13″，南北相距29.0 km；最北端在中梁镇新发村，位于北纬29°46′36″；最西端在曾家镇西部的青木关林区，位于东经106°14′36″；最东端在滴水岩，位于东经106°31′35″，东西相距24.3 km。本文以歌乐山街道中的一段排水管网为例，对其进行城市雨水排水管网改造优化研究。

3 方法

本文的主要目标是开发一种方法，通过将数学优化和雨水排放网络的水力分析相结合，找到最合适的管网修复解决方案。使用与不同预测结果相对应、基于气候变化研究的降雨情景，有潜在危险的场景需要被列入考虑范围。此外，必须对降雨-径流转换进行初步研究，以便水力模型将流量数据直接提供给模型的输入节点。换句话说，降雨径流转化的研究是独立于水工模型进行的，应该以网络的校准数学模型为起点，每个场景的分析都必须准确。选择SWMM5模型作为水力模型的模拟器。所选用的数学模型应尽可能简单、使优化过程的速度合理。

优化问题的解可以用成本来表示。在优化问题的第一个公式中，第一步将是找到转换以成本表示的水力变量值的函数。从这些假设出发，综合考虑对蓄水池的投资和对管道的改造，以及与排水管道水位超标的不同处罚函数。研究目标通过优化问题的目标函数表示，如式(1)所示：

(1)

在式(1)中，第一项反映了对应于系统N个节点中每一个的淹没体积VI(i)的成本。这个总节点数是结点数和蓄水池数之和。第二项是建造或扩大最终安装在系统上每个蓄水池的体积VDR(i)相关的投资成本，这些蓄水池要么是现有的，要么是即将安装的新池子。第三项是在修复中M管线过程中的预算。第四项是模型中M个管线中每个管线内的最大水量之和，将网络的持水量水平作为列入考虑的主要目标之。在式(1)中，每一项都有一个拉格朗日乘数λi。这决定在每个修复过程中使用的目标函数项。

通过结合蓄水池和管道改造来修复排水网络的方法基于以下阶段：建立网络的数学模型；定义潜在的决策变量(DV)；定义(1)中每个元素的成本函数。这样的过程可以提供网络的最终设计方案。优化过程中考虑的决策变量如下：与蓄水池有关的变量。如果初始模型包括一个蓄水池，则优化其横截面。其等效横截面S根据以下表达式(2)进行建模：

S=AZB+C

(2)

式中：A、B和C是调整截面以适应不同表达式的特征系数；z是水箱中的水位。如果储罐有一个恒定截面，则参数A代表该截面，B和C为0。

与节点相关的变量：该过程需要选择几个节点，以便考虑是否安装蓄水池。这些节点都具有与在该点安装蓄水池的横截面S相关联的决策变量，故该部分也由式(2)表示。

与导管相关的变量：该过程需要选择一些直导管，用以研究另一条不同维度的导管代替它们产生的效果，因此有一个决策变量与导管的直径相关联。需要修复的蓄水池和导管的数量将与决策变量一样多。

3.1 成本函数

公式(1)中定义的运营成本包含四个罚函数，分别代表每个决策变量成本与修复过程中限制相关的处罚。与决策变量相关的成本是蓄水池和管道的成本，而与修复过程相关的成本是排洪成本和管网蓄水成本。

3.2 投资成本函数

主要投资成本与建造蓄水池有关。蓄水池建造成本取决于许多因素：其横截面和尺寸；其类型(如由混凝土构成)，在蓄水池顶部承载的载荷；正常运行所需的辅助元件；清洗和维护蓄水池所需的成本等。对于本文所考虑的优化问题，作为主要因素，只考虑了成本和蓄水池容积之间的关系。可以用式(3)表示：

(3)

式中：C(VDR)是建造容积为VDR蓄水池的成本；其中τA、τB和τC是调整系数。网络修复预算中的另一项是用新管道替换某些旧管道。

为了评估安装新管道的成本，给出了一种以管道直径表示成本的函数：

(4)

公式(3)和(4)的参数值取决于所研究区域的价格数据库。为了确定参数，对成都市和重庆市的价格进行了研究。参数情况见表1。

表1蓄水池和导管成本参数的设定值

3.3 排洪成本函数

在目标函数中，还必须包括考虑排洪成本函数。定义了两种表示这种成本的方式：与每个节点的洪泛量成比例或与总洪泛水平成比例。在成本与洪水量成比例的情况下，可以简化为一个更简单的模型，其中收取的成本与模型每个节点中流出的水量成比例。相反，在费用与洪水水位相关的情况下，必须预先定义每个节点中的洪水区域。从洪水水位出发，需要定义一个函数，该函数将排洪成本与排水管网外的水达到的最高水位联系起来。

排洪成本的研究建立在易损性曲线的基础上，该曲线确定了达到水位的函数中的损害百分比。这条曲线与每平方米的土地使用成本相交。结果给出了一组不同的成本曲线(图1)，每条曲线都由特定的用途(商业或工业)或区域定义。

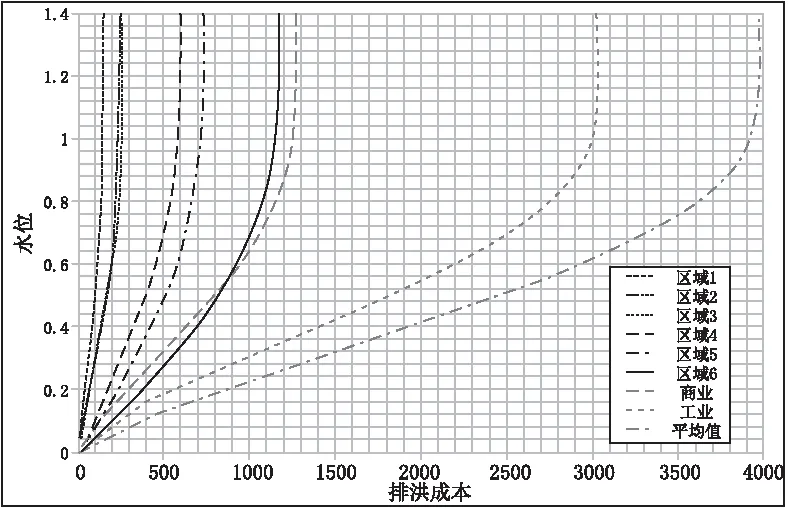
图1 不同区域与用途的排洪成本

为了总结图1中定义的成本函数规律，给出了一个数学表达式：

(5)

式中：Cmax反映了当洪水水位达到ymax时的最大成本；y是洪水水位；λ、b是调整系数，其最符合图1结果的参数是λ=4.88，b=0.65。

该参数代表了基于土地使用的单位面积最大成本，见表2。

表2 不同情况下的的Cmax系数取值

4 案例研究

为了证明给出方法的有效性，将其应用于歌乐山街道中的一段排水管网的修复中。该网络的简图见图2。

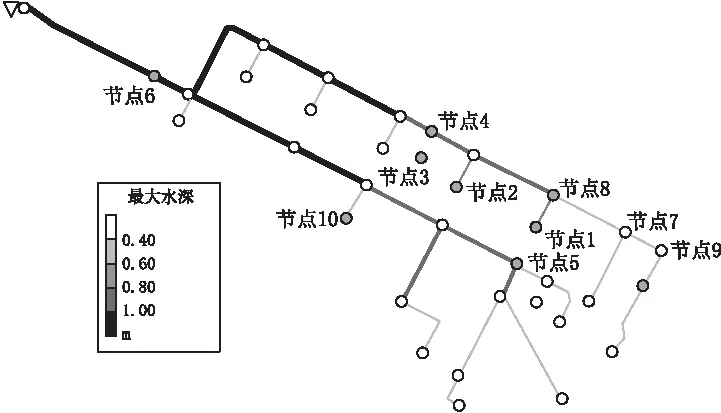
图2 网络的简图

在对网络优化之前，进行了初步分析，以了解网络状态及其对设计降雨的响应。使用SWMM模型进行水力网络分析，检测一些节点(图2的红色节点)中的洪水。表3中给出了不同节点的泛洪结果。在表3中，观察到排水系统的总洪量约为3761 m3，占设计暴雨产生所有径流的16%。

表3 节点泛洪的结果

对网络的初步分析表明，它不足以排出设计洪量。因此应用优化算法，考虑了以下场景：

场景1，网络修复基于更改网络导管并将其替换为不同的直径。此方案有35个决策变量，即直径未知的管道。场景2，仅安装蓄水池的网络修复。该方案也具有35个决策变量，对应于可以安装蓄水池的35个节点。方案3，结合安装管道和蓄水池的网络修复。决策变量的数量为70个。

表4给出了每种情况下的成本情况，包括：目标函数、排洪成本、管道和蓄水池成本以及蓄水池和管道数量。可以看出，联合实施管道修复和修建蓄水池是结果更好的解决方案。

在图3中，给出了场景3中要安装的蓄水池和要更换的管道情况，在该场景下，需要更换的管线数量为2，要安装的需水量数量为5，其中S代表蓄水池的底面积，Φ代表了管道尺寸的变更情况。

表4 每种情况下的成本和蓄水池及管道数量汇总

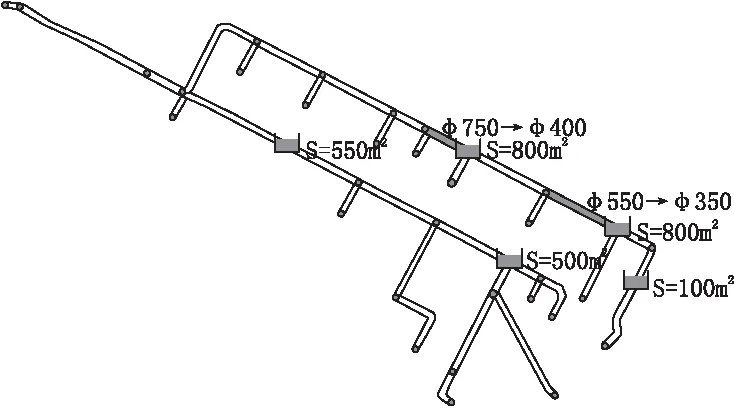
图3 优化结果(场景3)，新建的蓄水池和管道更换的方案

5 结论

本文给出了一系列排水管道网络的修复方案，并分析了它们在具体案例中的应用后，得出以下结论：使用实际雨水管网的原型作为起点，建立了包括惩罚成本函数、投资成本函数与排洪成本函数的模型，通过SWMM模型对管网进行水力分析，给出了十个节点洪泛的结果。设置了仅改造管网、仅新建蓄水池和改造管网和蓄水池同时修建的三种场景，采用遗传算法对不同场景进行寻优计算，结果表明，场景3无论是从排洪成本、管道、蓄水池成本以及蓄水池和管道数量来看，都表现出了节约工程量以及经济的优点，故联合实施管道修复和修建蓄水池是本问题最优的解决方案。