库威水文站河流糙率分析及应用

徐 伟

(新疆阿勒泰水文勘测局，新疆 阿勒泰 836500)

1 问题的提出

河流糙率是反映河段形态、河床面粗糙程度影响水流流态的阻力系数，对于天然河段而言无均匀流条件，所以糙率分析通常以天然河道单一形态河段为基本点。一般水文站河段因近似满足均匀流公式，所计算出的单断面糙率结果精度较差，不具代表性。根据相关研究，由于不同河段实际条件并不相同，在分析和计算天然河道河段糙率时，必须将河道平面形态、断面几何形式等均考虑其中。就断面几何形态这个因素而言，其不只作用于一个断面，而是在一个相当长的河段内影响河道糙率。与此同时，从单河段出发对所确定的断面流速不均匀系数及局部损失系数进行比较，也表明在天然河道沿程损失规律分析的过程中必须要考虑河道平面形态和断面几何形式等因素。此外，采用曼宁公式进行分析时，其中的水力半径R(通常用平均水深代替)、河道比降I、断面水流流速V等参数的变化不仅受河床粗糙程度的影响，还与河道平面形态、断面几何形式等有关。据此，在进行天然河道糙率确定时必须全面定义，通过探求河道糙率变动趋势规律选择适应的糙率计算公式，以增强糙率取值的代表性和应用方面的精度价值。

额尔齐斯河河源区卡依尔特斯河流域位于额尔齐斯河正源以西，为额河一级支流，流域在阿尔泰山中段以南，且呈南低北高态势，流域海拔最高3851.2m，最低为1416.8m，流域集水面积2534.6km2。卡依尔特斯河流主要为沙壤土质，土壤层分布较浅，且地表植被覆盖率较高，阳坡主要为灌木丛和草地，阴坡则为森林。流域内冬季最低温度可低至-49.5℃，且11月-次年4月期间流域为雪季，历年最大积雪深度可达1.2m及以上。流域内洪水过程通常出现在5-7月，其中6月径流量最大；10月-次年4月期间流域主要处于枯水期。近年来，在全球气候变暖、人类活动等因素的综合影响下，流域内冰川积雪消融过程明显提前，尤其是5月份径流量呈明显增大趋势。卡依尔特斯河流域库威国家基本水文站是中科院寒区旱区与工程研究所于2011年8月所建立的积雪-冻土-水文综合观测场站，主要观测项目包括温湿度、风速、风向、降水等，其完善的水文要素观测体系为文章分析提供了充足的数据资料。

2 糙率计算方法

水力学将水流分为稳定流和不稳定流等情况，稳定流又包括均匀流和非均匀流两种。结合库威水文站历年水文观测资料，其历年洪峰峰顶水位-流量关系呈现出明显的单一曲线形态，故可将其洪峰峰顶持续时间内水位近似视为平稳状态，即为稳定流，从而进行流域均匀流和非均匀流两种流态下河道断面糙率的分析。

河道单断面糙率值按下式确定：

(1)

不考虑局部损失的河段糙率值按下式确定：

(2)

考虑局部损失的河段糙率值按下式确定：

(3)

3 糙率规律及精度分析

河段及断面糙率是比降-面积法推流过程中结果精确度的控制性参数，在具体分析中，糙率取值之差往往会引起4.0%甚至更大的误差，而无法达到实际应用过程中对糙率精度的要求，为保证糙率取值的精确度，文章必须进行河段糙率变动趋势规律的分析。通过对库威水文站2011年8月建站观测以来-2020年年底水文资料的分析，糙率均受到河床粗糙程度、河道平面形态、岸壁特性、断面几何形式等多因素的综合作用，且对于不同河道和断面各类因素主次作用不同，文章取测次较多的单河段水文资料并采用式(1)-(3)进行河段水深均值、宽深比、比降、糙率等的计算(结果见表1)，并根据计算结果进行上述因素影响河段糙率程度的分析。

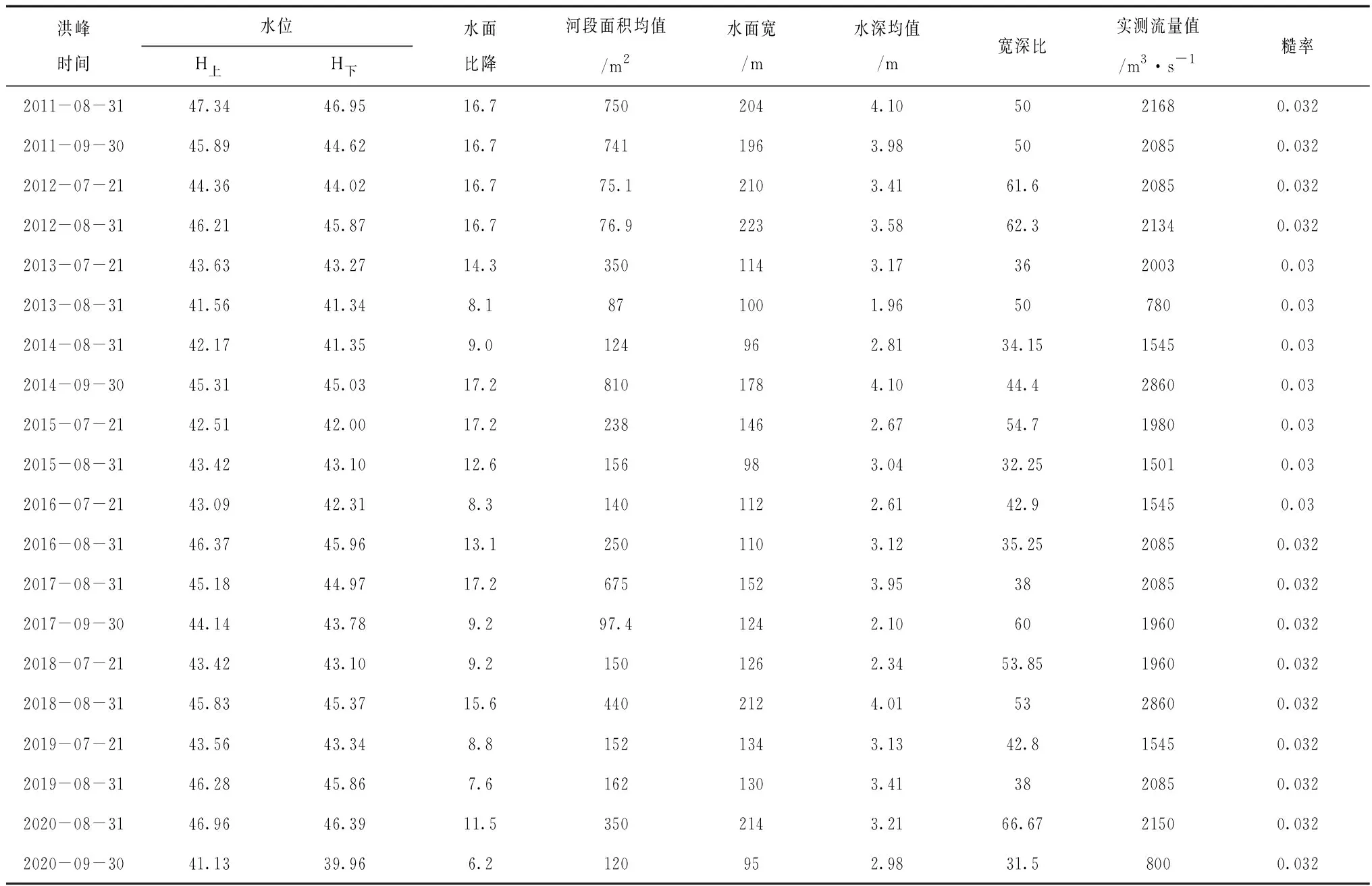
表1 库威水文站测次较多的单河段糙率计算结果

表2 库威水文站定线法对比误差

根据以上分析，单断面糙率和根据河段特性所求得的糙率存在一定程度的误差，且单断面计算仅适用于分析河段为均匀流的情况，对于非均匀流河段则无法通过单断面结果予以反映，应根据河段特性进行糙率计算。可见，水文计算中常采用的单断面糙率值的计算精度有待商榷，对于顺直且无明显流态变化的天然河段是否考虑局部损失的糙率值并无多大差异，其局部损失可以忽略不计，但是，对于因弯道、深潭等较多、局部损失较大的河段，必须考虑局部损失。

4 各参算要素测验误差的消除及新糙率推求

4.1 水面比降测验误差的定线消除

对于边界条件稳定的天然河道同水位的水面比降为常数，但因实测比降资料缺乏精度，其点据分布往往较为散乱，为此，文章点绘水位-比降关系曲线(见图1)并通过常规方法定线以消除比降观测结果的随机误差，并用消除测验误差后的水面比降(表3)替代实测比降值，避免糙率计算过程中比降资料误差的传递[2]。

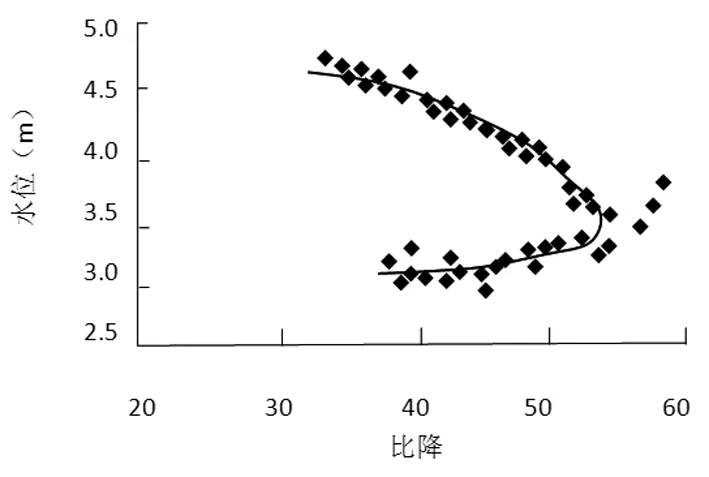
图1 库威水文站实测水位-比降关系曲线

4.2 流速、面积及水面宽测验误差的定线消除

根据相关结果，天然河道具有较好的水位-流速关系，考虑到库威水文站河床稳定性好，历年水文资料所显示的冲淤变化并不大，根据所点绘的水位-面积、水位-水面宽等关系曲线(图2-图4)发现，其线性关系较好。同样采用常规方法定线以消除观测结果随机误差后的流速、面积、水面宽值见表3。

图2 库威水文站实测水位-面积关系曲线

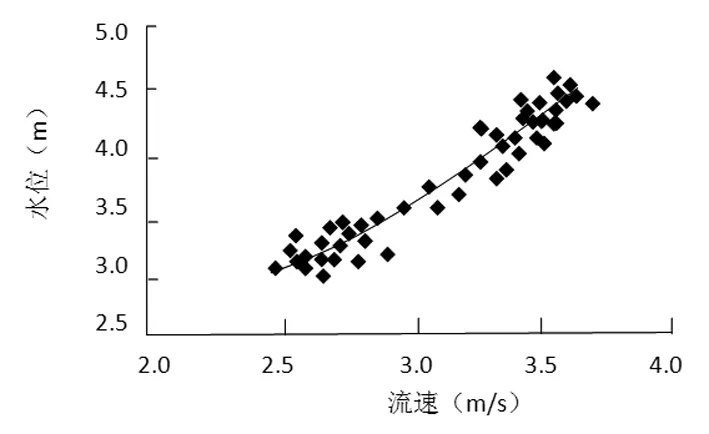
图3 库威水文站实测水位-流速关系曲线

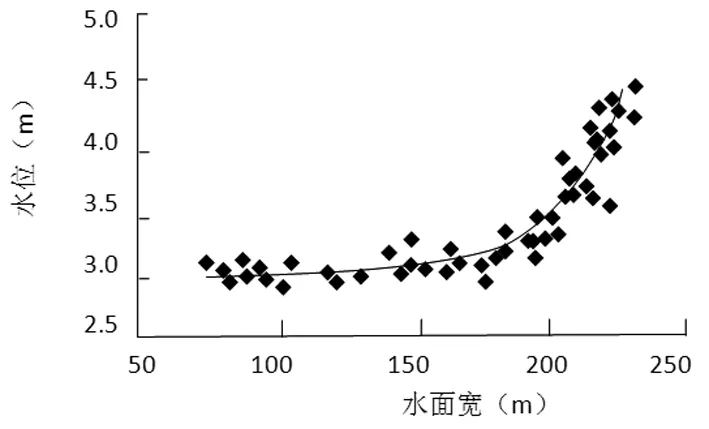
图4 库威水文站实测水位-水面宽关系曲线

4.3 新糙率的推求

将通过常规方法定线以消除随机测验误差后的各参算要素取值带入曼宁公式可求得消除测验误差后的新糙率，结果见表3，新糙率取值与原糙率误差完全满足水文规范中比降-面积法所推算糙率精度要求[3]。

表3 各参算要素测验误差的消除及新糙率推求

5 结 论

由文章分析结果表明，在诸多客观因素的影响下，天然河流比降观测结果精度不高且不具代表性，主要原因在于一般水文站河段比降段长度不够，影响比降精度，且在非稳定流情况下进行比降观测，会因观测时间和方法方面的差异而引发比降观测结果的较大误差。基于此文章通过常规方法定线进行了各参算要素测验误差的消除及新糙率推求，结果表明，比降-面积法具有较强的试用价值，且通过文章所提出的消除测验误差的方法能显著提升比降-面积法的应用精度和实用价值。