不同应变模型在沥青混凝土中的适用性研究

2021-07-15刘珊珊

黑龙江水利科技 2021年6期

刘珊珊

(齐齐哈尔市江东灌涝区服务中心，黑龙江齐齐哈尔 161001)

1 绪论

沥青混凝土具有非常好的抗渗性能，作为柔性材质，水工沥青混凝土适应变形的能力很强，目前我国水利工程中沥青混凝土作为防渗体应用广泛。沥青混凝土面板防渗断面形式分为简式和复式，复式断面结构分为封闭层、上防渗层、排水层、下防渗层、整平胶结层共5层结构，简式断面则省略排水层和下防渗层[1]。封闭层的作用是防止上防渗层因空气、水等外界环境的老化作用，一般采用沥青玛蹄脂；上防渗层采用密级配沥青混凝土，作用是阻止入库渗水，整平胶结层是冬雨季节保护碎石垫层，同时作为防渗面板基础层，优化调整下防渗层厚度，确保大坝防渗面板的材料完整性和构造连续性；整平胶结层一般采用粗级配沥青混凝土。

2 弹性模型对应力应变的分析

2.1 完全理想弹塑性模型

塑性力学可将应力应变关系进行曲线简化如下：

应力应变关系符合以下公式：

(1)

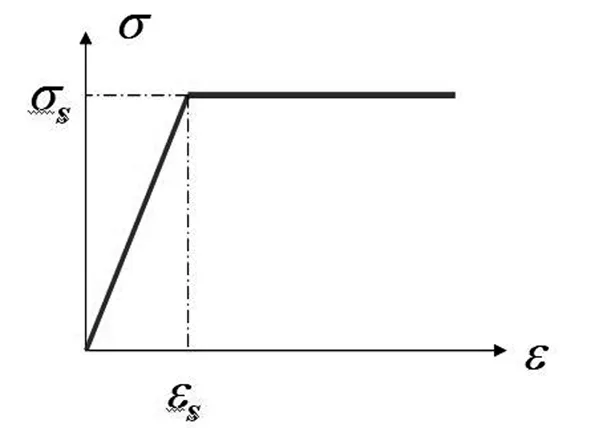
图1 理想弹塑性简化模型

2.2 用完全理想弹塑性分析沥青混凝土拉伸

为使试件性能接近沥青混凝土面板的现场实际碾压性能，采用板式成型方法[2]，将160℃±5℃的热混合料装入模具中，模型尺寸250×125×50mm，混合料插捣均匀铺平后击实，待试件冷却至室温后进行脱模，3个试件为1组，试验前先测定试件孔隙率。

图2 切割后的拉伸试件

本次直接拉伸试验温度为2℃，按加载速率1mm/min进行加载，也就是1%的应变率每分钟。

表1 2℃条件下应变率1%拉伸试验结果

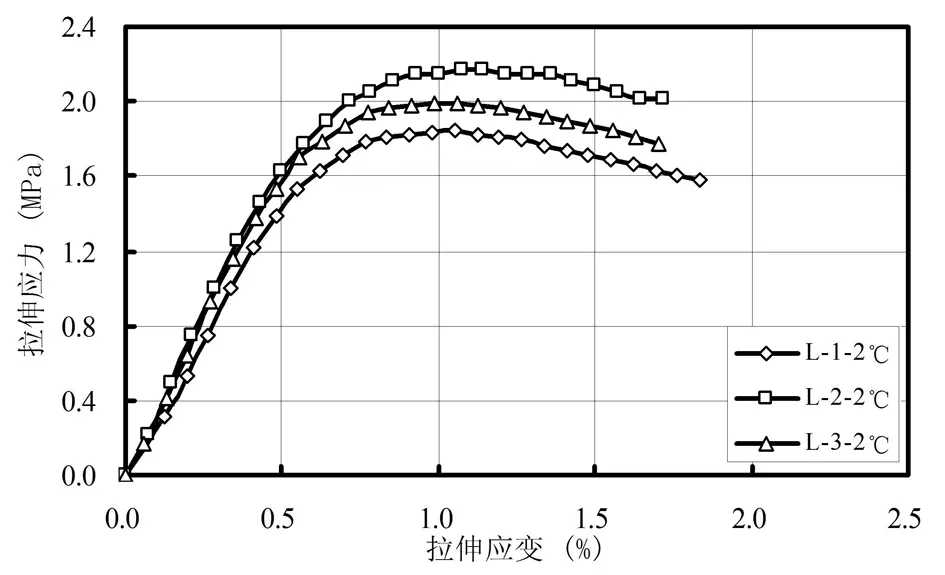
图3 2℃条件下应变率1%实际拉伸试验应力应变曲线

表2 2℃理想弹塑性拟合拉伸试验结果

3 线弹性模型对应力应变的分析

3.1 线弹性应力应变关系

若材料处于线弹性阶段，即σ<σp，则应力应变成比例关系：

σ=Eε

(2)

若材料只受剪切力，在线弹性阶段τ<τp，则剪应力与模量关系式为τ=Gγ,G为剪切弹性模量。平面应力状态表达式为：

(3)

3.2 线弹性分析拉伸

本次直接拉伸试验温度为11℃和25℃，按加载速率1mm/min进行加载，属于一维问题，拉伸应变等于试件伸长位移除以初始长度：

(4)

式中F拉伸荷载；A试件断面面积；σt轴向拉伸应力：

(5)

式中：εt为轴向拉伸应变；s为轴向拉伸变形值；L为轴向量测标距100mm。

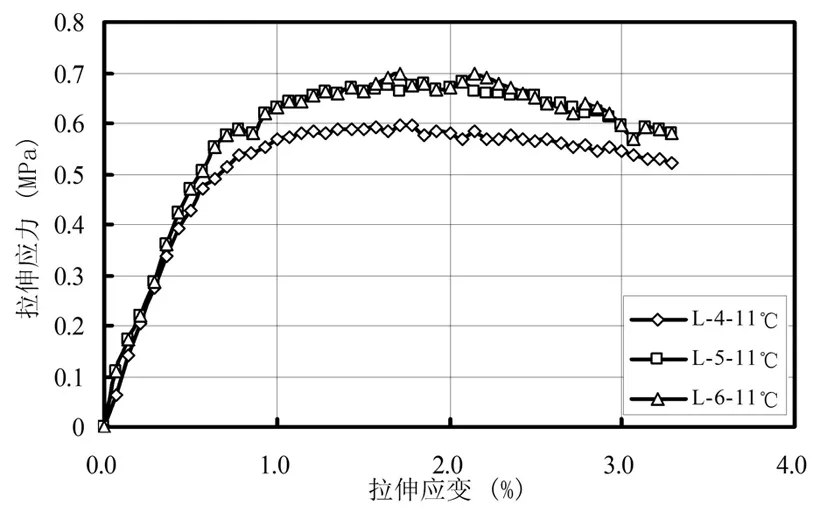
图4 11℃条件下应变率1%的拉伸应变曲线

图5 11℃线弹性性拟合拉伸试验

表3 11℃线弹性性拟合拉伸试验结果

3.4 小梁弯曲试验计算应变的验证

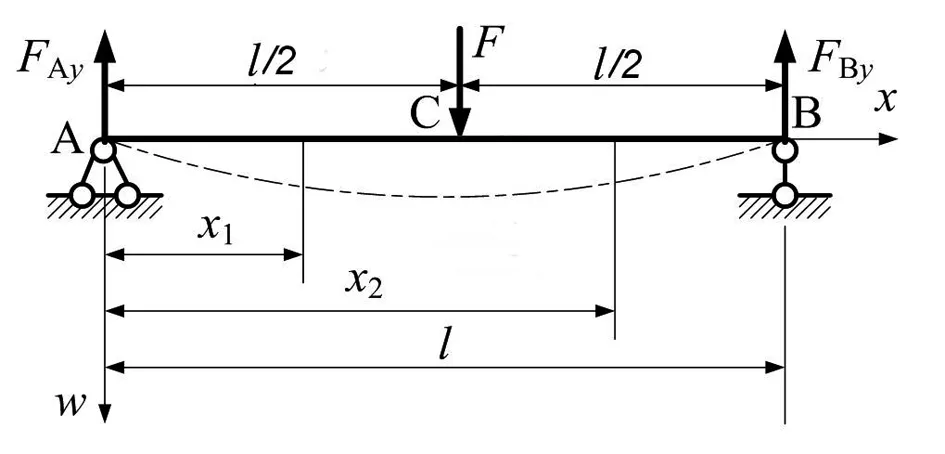
图6 跨中受集中力小梁弯曲示意图

对AC段分析A点的挠度为0，C点的挠度最大为

(6)

则AC段的平均挠度为

(7)

(8)

故AC段的平均挠度为C点挠度的5/8倍，近似应变AC段的平均应变应为C点的应变的5/8倍,由于轴对称，则全梁的下表面平均应变为中点最大应变的5/8倍。在小梁弯曲试件的侧面有效跨径上打上平行线，试验过程中用软钢尺测定梁下表面被拉长的距离，由于原跨径为200mm，记录当采集荷载达到最大值时的小梁有效跨径下表面伸长后的长度，可得实测的下表面变形的平均应变。可判定理论计算应变的准确性和理论计算模型的可行性[3-4]。

图7 弯曲试验后的小梁试件

从表4中可以看出，小梁弯曲试验时，在达到最大荷载时下表面的平均弯拉应变和理论计算的平均弯拉应变基本上是相符的，低温2℃时小梁弯曲的应力应变关系可以用完全理想弹塑性模型来计算，在较高温度像11℃和25℃时其小梁弯曲的应力应变关系用线弹性模型来计算是比较准确的。

表4 三种温度下小梁下表面实测平均应变和计算平均应变

3.5 综合分析结果

从表5可以看出同一温度下，压缩的强度远大于拉伸的强度，说明沥青混凝土是脆性材料，呈现出典型的耐压不耐拉，故而小梁弯曲时，一部分受拉，一部分受压，本质上是弯拉破坏。同一温度下同一应变率下，弯拉的应变大于直接拉伸的，但小于抗压的。当沥青混凝土以面板的形式出现时，要着重考虑其受弯拉时的特点，在同一应变率同一温度下，拉伸和压缩的弹性模量基本是相同的，但在对2度的弹塑性假定下，其弹性模量大于拉伸和压缩的，11度和25度时的弯曲弹性模量和直接拉伸与抗压时的较为接近。从温度方面看，当温度增高时，沥青混凝土强度明显降低，应变明显增大，弹性模量明显降低。