城市公园商品价值定量及影响因素——以南宁市南湖公园为例

杜延培，李在留，郭 松

（1.广西艺术学院，南宁 530007；2.广西大学林学院，南宁 530004）

公园作为城市生态环境建设的重要组成，其价值可分为舒适性的服务价值和商品性的经济价值［1］，从受益对象角度出发，前者称为“愉悦价值”，后者为“商品价值”［2］，相关价值定量已成为当前研究热点。其中，公园因优美的风景和舒适的环境，直接或间接卷入市场交易，带动经济发展，提高周边房地产价格，所形成商品价值无法直观体现，容易低估或忽视，导致城市建设和管理缺乏科学性［3］。基于公园的外部性特点［4］，市场化以外的享乐价格法（Hedonic price method，HPM）［5］为其商品价值评估提供思路。

HPM运行的前提条件是良好且透明度高的房地产市场，评估结果会根据函数模型的选择和分析步骤不同而有所变化，需要大量的数据和专业的数据统计分析以提高准确度，HPM的推广应用还有待进一步研究［6，7］。另外，城市绿地对周边的房地产有明显的增值作用，人们愿意为享受公园景观而支付更高的房屋价格［8-10］。受城市形态变化不一，房产价格受公园增值程度和影响因素不尽相同。目前，相关的研究大多数关注公园对周边房价的增值程度［11-15］，并未基于所得出的增值程度进一步评估公园所蕴含的商品价值。

南湖公园地处南宁市中心城区，总面积200.09 hm2，其中陆地面积93.09 hm2，水体面积107 hm2，是一座融水体景观、亚热带园林风光、市民娱乐休闲于一体的综合性公园，也是重大节日举行游园文化活动的重要场所。南湖公园作为“海绵城市”建设试点公园，政府投资巨大，基础设施完善，养护管理到位，深受游客喜爱，年接待游客达1 700多万人次，居南宁市免费开放型公园之首。因此，本研究选取南宁市南湖公园为研究对象，采集影响公园周边房屋增值情况的变量数据，检验并选取最优HPM分析模型，发掘显著影响公园周边房价的因素，计算公园溢出效应所产生的商品价值，为公园及周边城市规划建设提供科学依据，也为公园商品价值HPM定量研究提供实证。

1 研究内容与方法

1.1 样本采集

南湖公园所处市中心，周边多为老城区，几乎没有新开发的楼盘，因此以二手房为基础，参考前人研究经验［16-19］，选取以南湖公园为中心，2 km范围内300套二手房作研究样本。其中，公园周边1 km范围内为第一层，均匀选取200套二手房；公园周边1～2 km范围内作第二层，因房价受公园的影响较弱，均匀选取100套二手房。

1.2 变量选取

变量选取是HPM分析的关键，研究确定因变量为房屋出售单价，自变量为影响房价格的因素，包括建筑结构、区位特征、邻里环境3类［20，21］；由于地域特征、生活习惯、经济发展水平等差异，不同HPM研究案例选取变量有所不同［18］。本研究从南宁市南湖公园周边的实际情况出发，选取25个变量，其中，建筑结构有房屋建筑面积（S1）、卧室数量（S2）、客厅数量（S3）、卫生间数量（S4）、厨房数量（S5）、阳台数量（S6）、建筑年龄（S7）、总楼层数（S8）、所在楼层层次（S9）、是否带电梯（S10）、房屋朝向（S11）、装修程度（S12）12个变量；区位特征有离朝阳商圈距离（L1）、离南宁火车站距离（L2）、离南宁火车东站距离（L3）、离最近地铁站距离（L4）、离青秀山风景区距离（L5）、离邕江距离（L6）6个变量；邻里环境有离最近综合医院距离（N1）、离最近重点小学距离（N2）、离最近重点中学距离（N3）、离最近高等院校距离（N4）、离南湖公园距离（N5）、离最近其他开放公园距离（N6）、是否可见南湖（N7）7个变量。

1.3 数据获取

25个变量数据获取来源于国内房地产租售平台安居客网站上的二手房挂售信息和ArcMap 10.5软件测算。为保证网站数据的同一市场条件，于2019年11月22日至29日选取挂售时间在11月内的二手房数据信息，所选二手房均有真实照片展示，出售单价接近于小区平均值，价差控制在±10%以内。所选样本的区位特征和邻里环境类变量中，与距离有关的特征变量数据通过ArcMap10.5软件基于Google Earth卫星图测算得来，样本位置均在小区的中心点。其中，房屋样本、火车站、火车东站、地铁站用“点”的形式，朝阳商圈、青秀山风景区、邕江、综合医院、重点小学、重点中学、高等院校、南湖公园、其他开放公园用“面”的形式，通过ArcMap 10.5软件的“近邻分析”获取房屋样本与相关变量的最近距离。

变量数据中不能直接使用的如所在楼层层次（S9）、是否带电梯（S10）、房屋朝向（S11）、装修程度（S12）、是否可见南湖（N9）等需要进行量化赋值处理。其中，所在楼层层次（S9）中，低层为“1”，高层为“2”，中层为“3”；是否带电梯（S10）和是否可见南湖（N9）中，是为“1”，否为“0”；房屋朝向（S11）中，南北朝向为“3”，南朝向为“2”，其他朝向为“1”；装修程度（S12）中，毛坯为“1”，简装为“2”，精装为“3”，豪华为“4”。

从变量设计与统计信息（表1）可知，采集二手房单价均值13 586.78元/m2，较符合南湖公园周边实际行情；其变异系数为0.196，体现公园周边二手房售价存在明显差异。在二手房的建筑结构、区位特征、邻里环境3个变量中，变异系数普遍较大，一方面体现公园周边住宅建筑存在差异，社会资源分配并不均衡；另一方面反映公园周边住宅价格因建筑结构、区位特征、邻里环境等不同而存在差异。

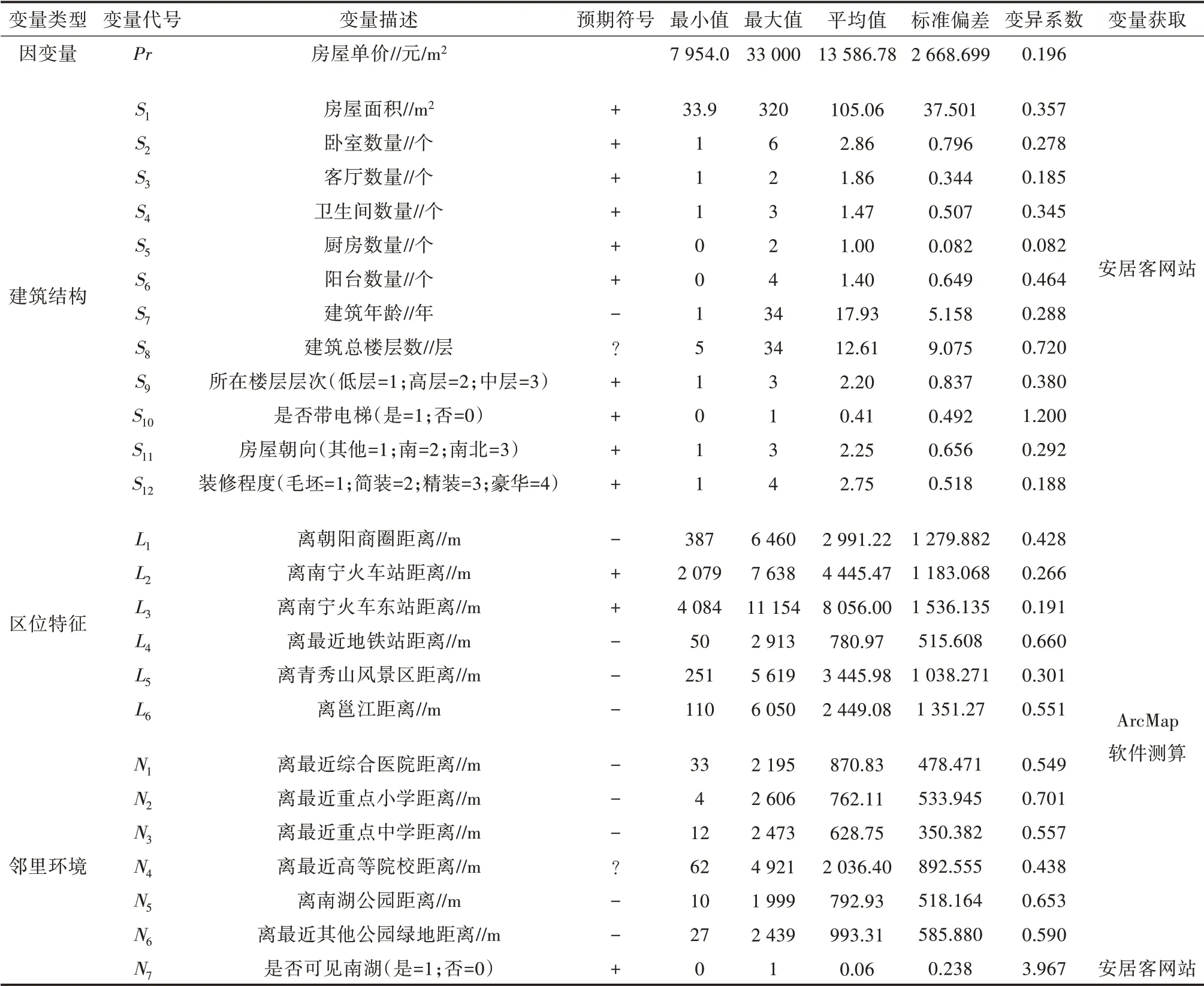
表1 变量设计与描述性统计结果

1.4 模型选择

HPM依靠计量经济学分析，其函数形式有线性模型、半对数模型、对数线性模型、二次模型、指数模型等［22，23］，研究选择在房地产研究中拟合程度较高的线性模型、半对数模型和对数模型进行分析［24］。

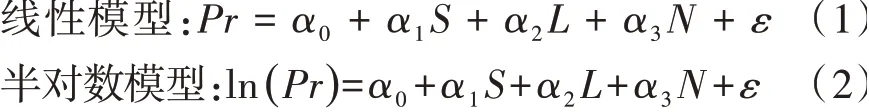
对数线性模型：

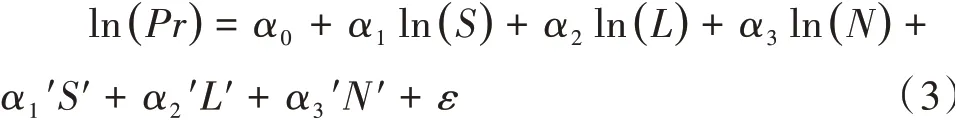
式中，Pr为房屋的单价，S为建筑结构，L为区位特征，N为邻里环境，α1、α2、α3分别为模型系数，α0为常数项，ε为误差项，L′、S′、N′为建筑结构、区位特征、邻里环境中进行量化赋值的变量，α1′、α2′、α3′为模型系数。注：“+”、“-”表示预测各变量对房屋单价的正、负影响，“？”表示预测正负影响不确定

2 模型分析

2.1 模型拟合比较

利用SPSS22.0软件分别对线性模型、半对数模型、对数线性模型采用输入回归的方法进行多元回归分析，3种模型拟合参数比较见表2。通过判定系数R2衡量回归方程的拟合度，R2值越接近1.000，模型拟合程度越好［25］，结果显示半对数模型的拟合程度要好于线性模型和线性对数模型；通过Durbin-Watson（U）值检验残差的自相关，一般认为该值在1.5～2.5，即说明模型残差无自相关现象，且值越接近2.0，模型残差间越相互独立，结果显示3种模型该值都接近于2.0，说明模型残差均无自相关现象；通过F检验模型回归关系的显著性，结果显示3种模型均为0.000，说明模型初步拟合均具极显著线性关系，其中半对数模型的F值为24.544，高于线性模型和线性对数模型；通过T检验3种模型P值均小于设定值0.05，呈显著性变量的半对数模型有15个，拟合精度最高；在共线性统计上，VIF值大于10的变量线性模型和半对数模型均有6个，线性对数模型有4个，说明3种模型中都有严重的多重共线问题，需要对共线变量进行剔除和处理。综合调整R2、F检验P值、F值、T检验P值、共线性VIF值来看，半对数模型的拟合效果最好，因此，选取半对数模型进行回归分析。

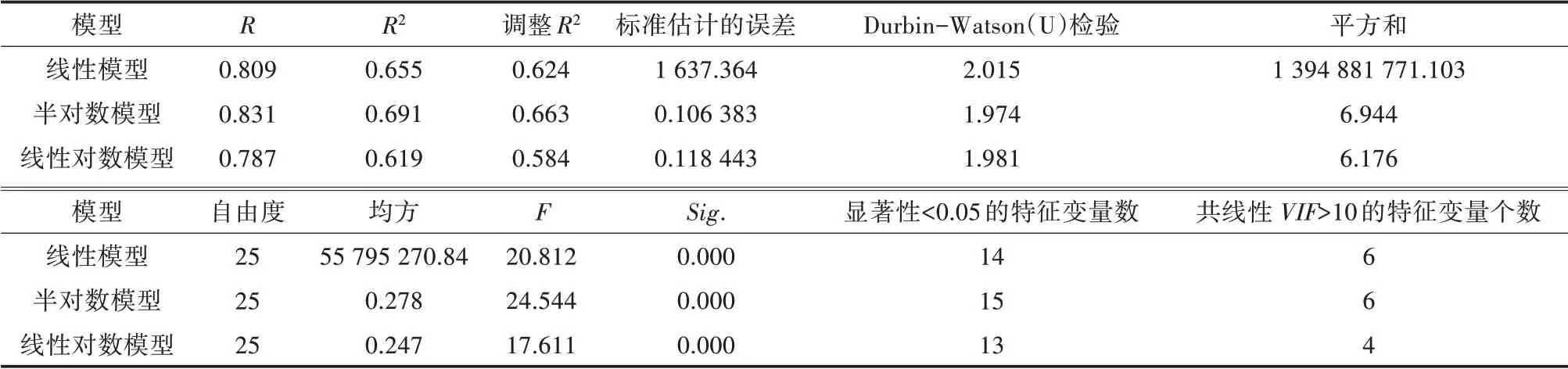
表2 模型拟合参数比较分析

2.2 回归分析与检验

在半对数模型初步回归分析中，存在部分变量相关性不显著（P＞0.05）、多重共线性（相关系数绝对值大于0.8）现象，需将造成多重共线现象的变量进行筛选剔除，再用逐步回归的方法进行多元回归分析。选取最优的回归子集，即显著性小于0.05的变量［26］，将方差膨胀系数VIF值大于10的变量，即离朝阳商圈距离（L1）、离南宁火车站距离（L2）、离南宁火车东站距离（L3）、离青秀山风景区距离（L5）、离邕江距离（L6）、离最近高等院校距离（N6）这6个在控制其他变量下进行偏相关分析，发现离朝阳商圈距离（L1）、离南宁火车东站距离（L3）与其他变量存在严重的多重共线性，剔除掉这2个特征变量再进行逐步回归分析，结果见表3。

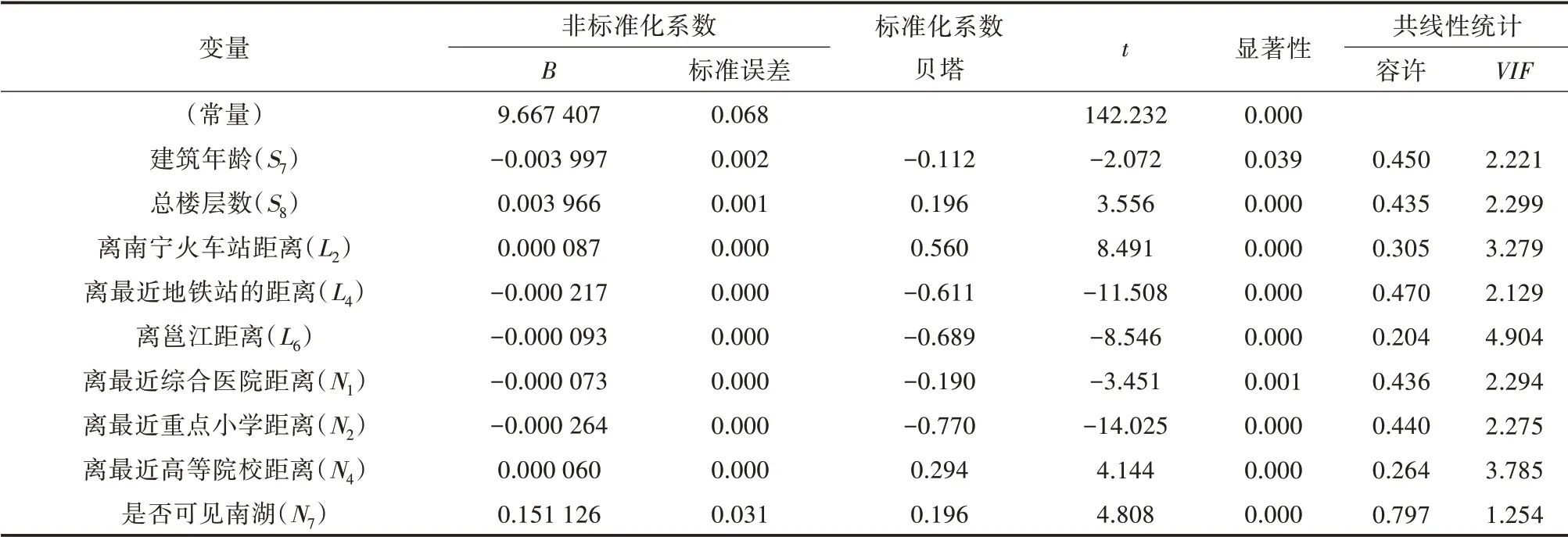
表3 半对数模型逐步回归系数

经拟合度检验，半对数拟合模型复相关系数R=0.784，判定系数R2=0.615，调整后的R2=0.603，说明模型拟合程度较好；经方差分析F检验，该模型显著性为0.000，说明因变量与进入模型中的自变量具有极显著的线性关系；经共线性诊断，最终进入模型的特征变量方差膨胀系数VIF值最大为4.904，在0～10的范围内，说明模型中的特征变量之间不存在多重共线性；经残差统计，标准化残差分布与估计曲线基本吻合（图1），说明了半对数模型逐步回归的标准化残差呈正态分布。以变量DEPENDNT作为X轴，变量ADJPRED作为Y轴，建立因变量与调节预测值的散点图（图2），散点分布基本呈一条直线，说明预测值与观测值很接近，预测效果较好。

图1 逐步回归标准化残差

图2 逐步回归预测值散点分布

3 结果与分析

3.1 影响房屋单价的因素

从表3可知，最终进入半对数模型的最优回归子集的变量有建筑年龄（S7）、总楼层数（S8）、离南宁火车站距离（L2）、离最近地铁站距离（L4）、离邕江距离（L6）、离最近综合医院距离（N1）、离最近重点小学距离（N2）、离最近高等院校距离（N4）、是否可见南湖（N7）9个，最终半对数模型为ln(P)=9.667407-0.003997S7+0.003966S8+0.000 087L2-0.000 217L4-0.000 093L6-0.000 073N1-0.000 264N2+0.000 06N4+0.151126N7。

根据回归系数B值的正负判断：房屋单价（Pr）与建筑年龄（S7）呈显著负相关（P＜0.05），与离最近地铁站距离（L4）、离邕江距离（L6）、离最近综合医院距离（N1）、离最近重点小学距离（N2）呈极显著负相关（P＜0.01），与总楼层数（S8）、离南宁火车站距离（L2）、离最近高等院校距离（N4）、是否可见南湖（N7）均呈极显著正相关（P＜0.01）。

半对数模型中的B值表示变量的绝对变化会引起房屋单价（Pr）的相对变化（变化率），变化率以自然对数e为底数，依据回归系数的反对数进行推导，结果表明，建筑年龄每增加1年，离地铁站口距离、离邕江距离、离综合医院距离、离重点小学距离每增加1 m，房屋单价（Pr）分别下降0.399%、0.022%、0.009%、0.007%、0.026%；建筑总楼层每增加1层，离火车站距离、离高等院校距离每增加1 m，拥有南湖湖景视线，房屋单价（Pr）分别增长0.397%、0.009%、0.006%、16.314%。

3.2 南湖公园商品价值估算

根据HPM的研究结果，是否可见南湖（N7）对房屋单价（Pr）增值16.314%，以计算南湖视线影响下的房屋溢价来估算南湖公园经济价值。具体过程：所选取300套二手房屋平均单价13 586.78元/m2，建筑总楼层数平均13层。根据国家统计局最新统计数据，城镇平均每户家庭人口为3人，人均住房面积39 m2，可计算城镇每户家庭的住房面积约为117 m2，常规房屋开间面宽12 m左右；南湖公园周长为9 378 m，假设周边全部建成平均为13层的商品住宅塔楼，塔楼每层有2套房屋阳台正对南湖，其塔楼的建筑宽度约为24 m；根据《城市居住区规划设计标准》GB50180—2018要求住宅侧面间距不小于13 m，计算得出南湖公园周围可建塔楼253栋；由于公园周边存在植物遮挡视线，植物平均高度按12 m计，4层以上房子的视野可见南湖湖景，可见南湖的房屋有4 554套。最终房屋溢价约为1 181 016 293.54元，即南湖公园商品价值约11.810亿元。

4 讨论与结论

4.1 讨论

1）不同研究对象周边的房产价格影响因素存在异同，南宁市南湖公园周边2 km房产价格的影响因素大部分与前人研究相似［9，10］，但离南湖公园距离因素在研究中并未对房产价格产生显著影响，其原因可能与南湖公园地处老城区，相关公共服务设施配套完善有关，如相邻近的金花茶公园、民歌湖公园、青秀湖公园、邕江滨水公园等弱化了南湖公园的单一影响，使得离南湖公园距离因素对房产价格影响不显著。

2）许多学者基于Hedonic模型的公园周边房产特征价格分析只得出影响因素及影响程度［12-14］，未进行公园的商品价值计算，本研究在前人研究的基础上，基于统计数据及实际情况做出合理假设，提出了计算公园“商品价值”的方法，同时也表明城市公园显著增加了周边房产价值。因此，政府部门应积极探索多样化的公园溢价回收模式。如将公园的溢出效应进行货币化定量，以此作依据，向公园周边地产开发商征收土地资产潜在增值作为公园建设维护的资金来源；此外，政府可与地产开发商联合起来进行公园规划建设，将公园建设融入住宅开发的全过程，达到家住公园的体验。由此，既能在实现房地产开发项目增值的同时为社会创造出可供市民休闲娱乐的公园，也可有效缓解政府的财政压力，实现政府、企业和市民的三方共赢。

4.2 结论

1）南湖公园HPM研究的最优模型为半对数模型，显著影响公园周边房屋单价（Pr）的变量有建筑年龄（S7）、总楼层数（S8）、离南宁火车站距离（L2）、离最近地铁站距离（L4）、离邕江距离（L6）、离最近综合医院距离（N1）、离最近重点小学距离（N2）、离最近高等院校距离（N4）、是否可见南湖（N7）9个。其中，建筑年龄越小、建筑总楼层越高，房屋单价越高；离火车站越远、离地铁站口越近、离邕江越近，房屋单价越高；离综合医院越近、离重点小学越近、离高等院校越远、拥有南湖湖景视线，房屋单价越高。

2）离南湖公园距离（N5）对房屋单价无影响，而是否可见南湖（N7）对公园周边房屋单价增值率为16.314%，基于假设前提下评估南湖公园所产生的经济价值约为11.810亿元，说明公园对周边房产增值溢出效应巨大。