On the crossing periodic orbits of a piecewise linear Liénard-like system with symmetric admissible foci
2021-07-15-,-
-, -
(School of Mathematics, Sichuan University, Chengdu 610064, China)
Abstract: We investigate the crossing periodic orbits of a piecewise linear Liénard-like system with symmetric admissible foci. By reducing this system to a normal form, which has less parameters, and constructing the Poincaré maps of the left and right subsystems, we prove the existence of at least one crossing periodic orbit, give a sufficient condition for the non-existence of crossing periodic orbits, and provide an upper bound for the number of crossing periodic orbits under some conditions.
Keywords: Focus; Normal form; Periodic orbit; Piecewise linear system
1 Introduction
Planar piecewise smooth differential systems are used as mathematical models in many fields such as power electronics[1]and feedback systems in control systems[2]. Because of the non-smoothness of vector fields, the qualitative analysis is much more difficult than smooth systems even for piecewise linear systems with one switching line
(1)
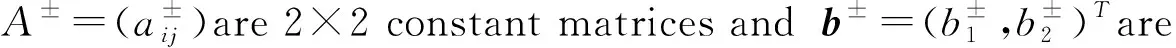

(2)
by
(3)
(4)
It is not hard to check that both equilibria of subsystems in System (4) are foci if and only if
(5)
The focus of the left subsystem is admissible (resp. virtual) if additionallya-<0 (resp.a->0). The focus of the right subsystem is admissible (resp. virtual) if additionallya+>0 (resp.a+<0).
For System (4), the existence of two crossing periodic orbits is proved in Ref.[3] when the two foci are virtual and the existence of three crossing periodic orbits is proved in Ref.[5] when one of these two foci is admissible and the other is virtual.
In this paper, we study the number of crossing periodic orbits for System (4) having two admissible foci. We reduce System (4) to a normal form and state our main result in Section 2 and give the proofs in Section 3.
2 Main results

Theorem2.1System (4) having two foci is equivalently transformed into
(6)
by (x,y,t)→(x/ω-,y,t/ω-),where


(7)
satisfying
αδa≠0,α2-4β<0
(8)
When there are two admissible foci, for System (4) we get an equivalent System (6), which has 6 parametersα,β,ρ,δ,a,b.Thus System (6) is regarded as a normal form of System (4). Observing that System (6) is invariant under the change
(x,y,t,α,β,ρ,δ,a,b)→(x,-y,-t,-α,
β,ρ,-δ,a,-b),
we only considerb≥0 in System (6). In the following, we consider the existence of crossing periodic orbits of System (6).
Theorem2.2Assume that the two foci of System (6) are admissible and symmetric with respect toy-axis. The following statements hold:
(a) For the caseδα<0, System (6) has at least one crossing periodic orbits ifδ2+1-β=b=0;
(b) For the caseδα>0, System (6) has at most two crossing periodic orbits and there existsM>0 such that for all |δ|>MSystem (6) has no crossing periodic orbits.
In Theorem 2.2, for the caseδα<0, we give a sufficient condition for the existence of crossing periodic orbits. However, it is hard to get a condition for the non-existence of crossing periodic orbits as we provide for the caseδα>0.Thus in the end of this paper we give two examples for the caseδα<0 to exemplify the possibility of non-existence of crossing periodic orbits. On the other hand, for the caseδα>0 we provide an upper bound for the number of crossing periodic orbits, but we are not able to judge if it is reachable.
3 The proofs of the main results
ProofofTheorem2.1By transformation (x,y)→(x/ω-,y), System (2) having two foci is transformed into
(9)
Further, by a time rescalingt→t/ω-System (9) is changed into System (6) with new parameters defined in (7). By (5), new parameters in system (6) satisfy (8).
In order to prove Theorem 2.2, we need some preliminaries. For the left subsystem in (6), the solution satisfies (x(0),y(0))=(0,y) is of the form

(10)
where

is the coordinate of the unique equilibrium of the left subsystem. For the right subsystem in (6), the solution satisfying (x(0),y(0))=(0,y0) is of the form
(11)


is the coordinate of the unique equilibrium of the right subsystem.
In the following, we introduce the Poincaré map, which is our main tool in looking for periodic orbits. Clearly, the right subsystem in (6) has a unique tangency point (0,b).Since the foci is admissible, the orbit starting from this tangency point intersectsy-axis for the first time at a point whenA>0.Thus the orbit starting from (0,y0)intersectsy-axis for the first time at (0,y2) fory0≤b.We denote the time bytRand define a right Poincaré mapPRasy2=PR(y0)for ally0≤b.From (11), we obtain a parametric representation of the right Poincaré mapPRas
(12)


(13)


From (12), we get
(14)
(15)
Since
sign(BsinhAtR-AsinBtR)=signA,
it follows from (15) that
(16)




Then
and
(1+e-Aπ/B)(b+2AxR).
Proposition3.2[5]Assume thatxL<0.Then the following statements are true for the left Poincaré mapPL:
(a) Ifδ≠0, thenPLis defined by




We have
Then
e(A/B+δ)π.


(17)


(18)

(19)


-e-Aπ/B+eδπ.

Lemma3.4Whenδ<0,A<0,b=0, System (6) with (8) has no crossing periodic orbits.


(1-μ)yL+μyU,0≤μ≤1},

μyL+(1-μ)yU,0≤μ≤1}.

2δσ-+2Aσ++bh=0
(20)
Since (20) cannot be fulfilled whenδ<0,A<0,b=0, System (6) with (8) has no crossing periodic orbits.
ProofofTheorem2.2The two foci of the left and right subsystems of (6) lie at (xL,yL) and (xR,yR),defined below (10) and (11), respectively. Since the two foci of System (6) is admissible, we geta<0 andρ>0.Note thatβ>0 by (8). Because of the symmetry of these two admissible foci with respect toy-axis, we get
a/(1+δ2)=-ρ/β, 2δa/(1+δ2)=αρ/β+b.
Then
ρ=-βa/(1+δ2),b=(2δ+α)a/(1+δ2)
(21)



which means that system (6) has at least one crossing periodic orbits. (a) holds.
For the caseδα>0,sinceb≥0,we haveδ<0,α<0 by (21). From Lemma 3.4, we know that Ψ(y)≠0 forb=0,so by continuity we get Ψ(y)≠0 for 0 In Theorem 2.2, we prove the existence of at least one crossing periodic orbits for System (6). The non-existence of crossing periodic orbits for some systems is proved for the caseδα>0.In the following, for the caseδα<0 we provide two examples to show that there may be no crossing periodic orbits no matterb=0 or not. Example3.5Letα=1,β=5/16,ρ=5/32,δ=-1,a=-1,b=1/2 in System (6),i.e., (22) It is easy to check that System (22) has two admissible foci at(-1/2,1)and(1/2,1).Sinceδ<0,by Proposition 3.2 (b) we obtain yA=(1+eAπ/B)(b+2AxR)=1+e2π. Hence Ψ(y)>0 and System (22) has no crossing periodic orbits. Example3.6Letα=2,β=10/9,ρ=5/9,δ=-1,a=-1,b=0 in System (6),i.e., Similarly to Example 3.5, we can prove that there is no crossing periodic orbits by similar analysis. Thus we omit its proof here.