深海海底钻机多支腿依次着底碰撞稳定性分析
2021-07-15邓斌刘德顺郭勇金永平王周洋
邓斌,刘德顺,*,郭勇,金永平,王周洋
(1. 湖南科技大学 海洋矿产资源探采装备与安全技术国家地方联合工程实验室,湖南 湘潭 411201;2. 湖南科技大学 先进矿山装备教育部工程研究中心,湖南 湘潭 411201)
深海海底钻机是开展海洋地质及环境科学研究、进行海洋资源勘探和海底工程地质勘察所必备的关键技术装备[1,2].开展海深1 km以上的深海海底钻进时,通过大型自带动力定位的母船搭载深海海底钻机,在指定的钻探点海面利用配套的铠装脐带缆绞车系统将深海海底钻机下放至海底,在钻机临近着底时支撑腿展开,然后钻机下落着底.目前国内对深海海底钻机着底碰撞的相关研究仍处于起步阶段,但哈尔滨工业大学、南京航空航天大学等几家单位针对火箭运载器[3-5]及月球探测器[6-8]着陆过程进行了较丰富的研究,而深海海底钻机与火箭运载器和月球探测器在着陆形式及动力学过程具有较大的相似性,因此火箭运载器和月球探测器着陆动力学相关文献对深海海底钻机着底有一定参考价值.
不同于月球探测器和火箭运载器采用软着陆方式,可以通过缓冲装置减速后安全着陆,深海海底钻机没有配备缓冲装置[9],直接以硬着底方式与海底表面发生碰撞.深海海底钻机与海底表面碰撞过程中,要承受巨大的冲击载荷或碰撞振动,由于冲击加速度过大可能造成钻机框架、传感器和通讯设备等发生结构破坏.凹凸不平的海底底质也可能造成深海海底钻机单组支腿着底或双组支腿着底时发生倾翻.
基于此,建立2-1着底模式下3腿支撑式深海海底钻机着底碰撞动力学模型模拟着底碰撞过程.在动力学模型基础上,确定深海海底钻机着底稳定性的评价标准.通过仿真计算,重点分析钻机初始姿态角和海底底质倾角对钻机着底稳定性的影响,并结合单组支腿着底稳定区间和双组支腿着底稳定区间得出2-1着底模式下深海海底钻机着底稳定域,为深海海底钻机选址和后期调平控制工作提供理论支持和操作参考.

1 深海海底钻机着底动力学建模
1.1 着底过程理论建模
3腿支撑式深海海底钻机按照依次接触海底的支腿数量及接触海底的次数可将着底模式分为1-2模式(1条支腿先着底→其余2条支腿同时着底)、1-1-1模式(1条支腿先着底→与其相邻的第2条支腿着底→最后1条支腿着底)、2-1模式(2条支腿同时着底→最后1条支腿着底)和3支腿同时着底模式.深海海底钻机着底模式如图1所示.
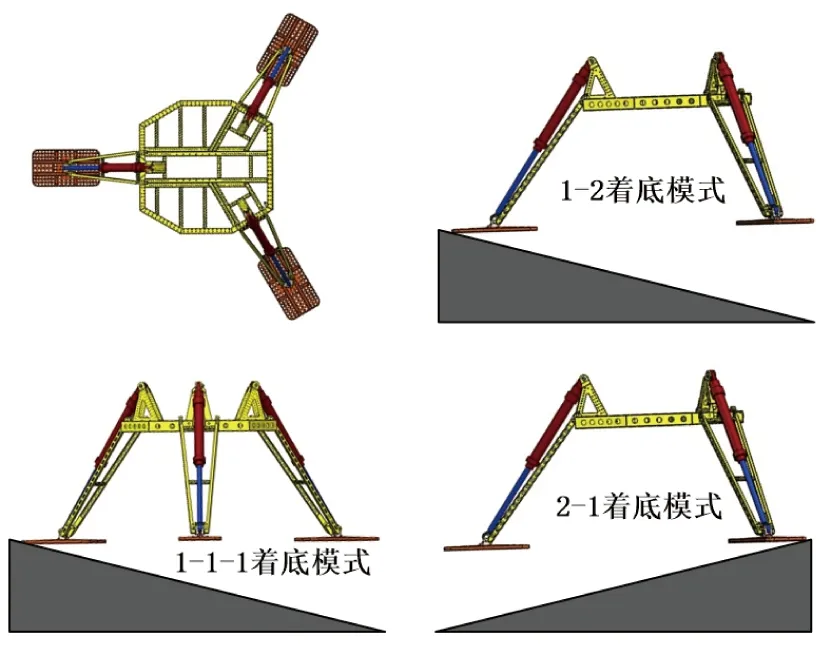
图1 深海海底钻机着底模式
在所有着底模式中,1-1-1模式为三维非对称着底模式,更趋近于实际着底,但由于海底地形地貌随机性大,1-1-1模式动力学建模过程复杂且难度大,因此该模式不具有普遍适应性.1-2模式和2-1模式动力学过程类似,为二维对称着底模式.所谓二维对称着底是指在着底前后深海海底钻机的运动都关于垂直面对称,即钻机的水平速度与垂直速度均在钻机几何对称面内.2-1着底模式作为最典型着底模式,其动力学过程往往具有较高的研究价值.
在2-1着底模式下,深海海底钻机着底过程为首先铠装脐带缆牵引深海海底钻机匀速吊放,然后深海海底钻机选址,最后释放铠装脐带缆,深海海底钻机自由下落.释放铠装脐带缆后的着底过程如图2所示.
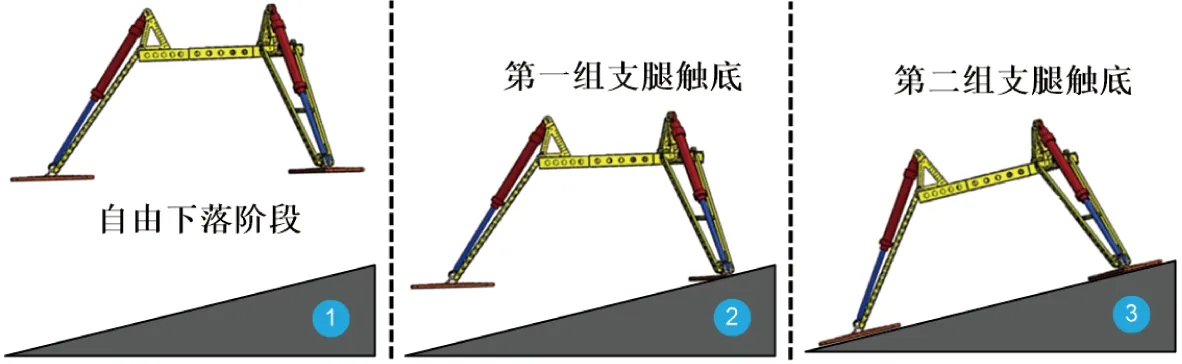
图2 释放铠装脐带缆后着底过程
1.2 深海海底钻机着底稳定性评价
深海海底钻机着底稳定性主要是指钻机与海底底质碰撞后,钻机各组成部件在冲击作用下不产生结构破坏或失效,不发生倾倒和翻滚,最终能够相对海底底质保持稳定状态.为了避免深海海底钻机在与海底表面碰撞过程中发生结构破坏或失效,通常要求冲击加速度不超过允许值.
对于深海海底钻机在着底过程中是否稳定的问题,根据静态稳定性理论分析:当深海海底钻机质心沿中心方向的投影在各支腿碰撞点投影范围边界外(含边界)且有相应的倾覆趋势时,则视为深海海底钻机发生倾翻(不稳定);反之,深海海底钻机稳定着底.建立的2-1着底模式下3腿支撑式深海海底钻机二维动力学模型,可将其着底稳定性判据简化为图3所示.
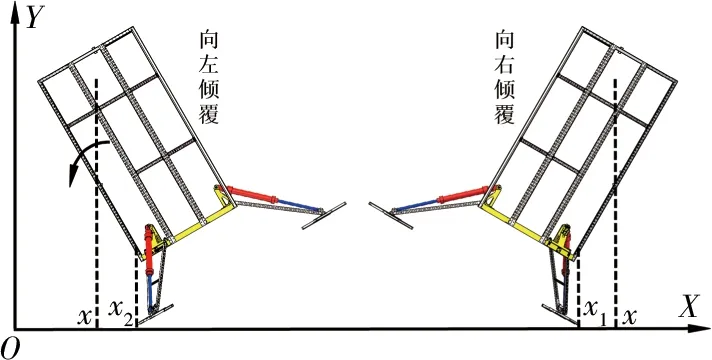
图3 深海海底钻机倾覆方式判断
深海海底钻机稳定着底评价标准可分为结构稳定和支撑稳定,其判据如下:
1)结构稳定判据:(1)结构稳定(深海海底钻机冲击加速度≤10g);(2)结构破坏(深海海底钻机冲击加速度>10g).
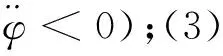
1.3 深海海底钻机自由下落状态动力学方程
深海海底钻机在匀速吊放过程中受海浪、海洋流速的影响姿态会产生一定的偏转,初始偏转姿态角为φ0.由于海洋流速随着海水深度的增大不断减小,随着深海海底钻机逐渐接近海底,海洋流速接近于0.考虑到释放铠装脐带缆后深海海底钻机下落历时很短,实际姿态角变化值很小,因此假设此阶段深海海底钻机以自由下落状态下落,其姿态角不发生变化.仅考虑y方向的海水浮力和海水阻力,此状态的动力学方程式为
(1)
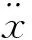
深海海底钻机下落过程中钻机与海水发生流固耦合作用,目前对流固耦合作用问题的力学模型主要有流固耦合模型和附加质量模型.对于流固耦合模型,Motora等[10]进行了大量模型试验和水动力分析,利用Morison方程计算海水阻力;对于附加质量模型,王自力等[11]利用Lagrange有限元法建立了船舶碰撞模型,采用附加质量的方法估算海水阻力,极大程度的节省了模型计算量.
采用附加质量模型,将海水阻力简化为附加质量的形式.通常假定海水的阻力为
(2)
式中:m1为x方向上附加质量,其值通常为钻机质量m的0.02~0.05倍,取m1=0.05m;m2为y方向上附加质量,其值通常为钻机质量m的0.4~1.3倍,取m2=0.4m.
在自由下落状态结束时,其受力分析如图4所示,深海海底钻机有关符号及其含义如表1所示.

表1 深海海底钻机力学模型有关符号及含义
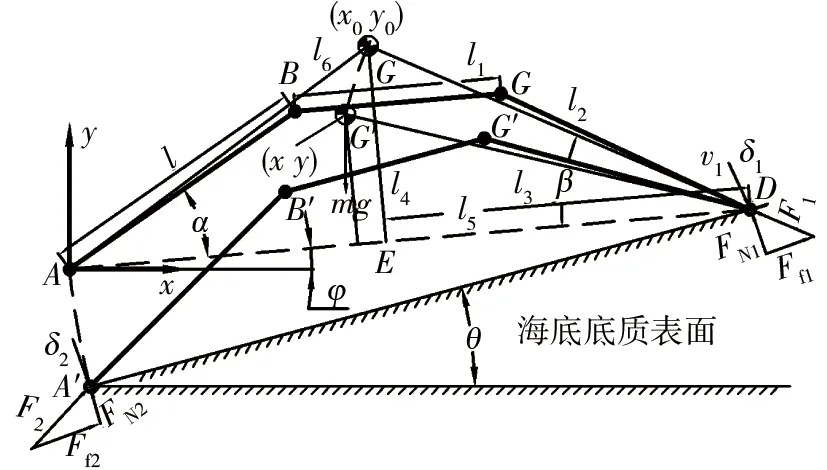
图4 深海海底钻机触底过程受力模型
此时深海海底钻机质心点G的坐标为
(3)
式中:φ0为深海海底钻机的初始姿态角.
当自由下落状态结束时,由能量守恒定律可知此时深海海底钻机的速度v1为
(4)
式中:h为钻机铠装脐带缆的释放高度;t1为钻机从自由下落至着底所需时间.
1.4 深海海底钻机第1组支腿着底状态动力学方程
深海海底钻机自由下落状态结束时,如若钻机姿态角不为0°或海底底质倾角不为0°时,深海海底钻机进入第1组支腿着底状态.此时,第1组支腿受到垂直海底底质表面向上的支持力和海底底质点的摩擦力,而第2组支腿仍处于悬空的状态,直到该支腿脚板接触海底,深海海底钻机进入双组腿着底状态.
第1组支腿着底状态动力学方程为
(5)
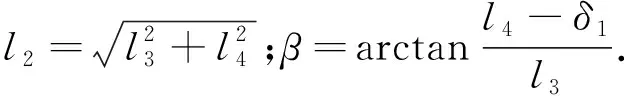
由图4可知,当深海海底钻机质心从G点运动至G′点时,第1组支腿着底状态结束,此时深海海底钻机质心点G′的坐标为
(6)
1.5 深海海底钻机双组支腿着底状态动力学方程
深海海底钻机进入双组支腿着底状态时,2组支腿均会受到支持力和摩擦力,随着深海海底钻机和海底底质之间的碰撞,支持力和摩擦力将会发生变化.此时深海海底钻机的动力学方程为
(7)
此阶段,深海海底钻机与海底底质发生碰撞,海底底质被挤压变形,深海海底钻机侵入海底底质一定深度.此时深海海底钻机质心的坐标为
(8)
深海海底钻机2组支腿水平位置可表示为
(9)
2 着底碰撞模型的建立
2.1 深海海底钻机着底碰撞模型
当深海海底钻机与海底底质发生碰撞时,其碰撞冲击力与碰撞时的相对速度、支腿的材料属性、海底底质的物理力学性能以及海底地形地貌等因素有关,且碰撞瞬间冲击力的变化十分复杂.因此,建立合理的碰撞模型,使之能有效表述深海海底钻机着底过程具有重大工程意义.基于深海海底钻机历次取样作业经验和数据,采用修正后的线性黏弹性碰撞模型(MLV模型),假设碰撞过程中深海海底钻机为刚体.深海海底钻机碰撞模型如图5所示.
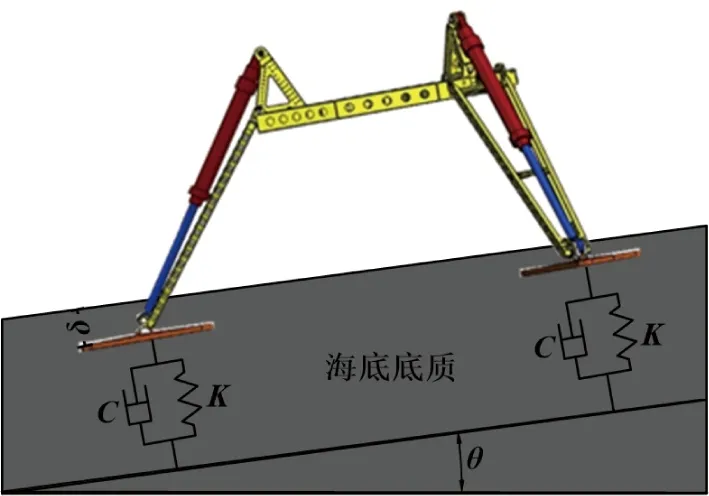
图5 深海海底钻机碰撞模型
深海海底钻机总碰撞冲击力表达式为
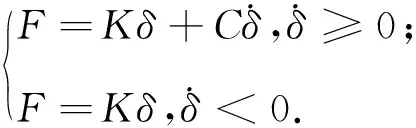
(10)
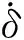
采用MLV模型在确定碰撞参数时,通常通过现场试验测得,结合深海海底钻机历次作业沉陷深度近似取K=2×105N/m,阻尼系数C为
(11)
式中:m1,m2为两碰撞体的质量;ξ为碰撞阻尼比,ξ的表达式为
(12)
式中:e为恢复系数,取e=0.2.
使用MLV模型模拟碰撞过程时,可将其近似为一个单自由度系统,其动力学方程为
(13)
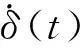
2.2 深海海底钻机各组支腿受力分析
实际碰撞时,深海海底钻机与海底底质碰撞主要发生在腿部,由于钻机初始姿态角和海底底质倾角的存在,钻机2组支腿受到的碰撞力并不相等.为进一步求得各组支腿所受碰撞力的大小,假设深海海底钻机支腿脚板与海底底质发生垂直碰撞.其碰撞过程受力分析如图6所示.
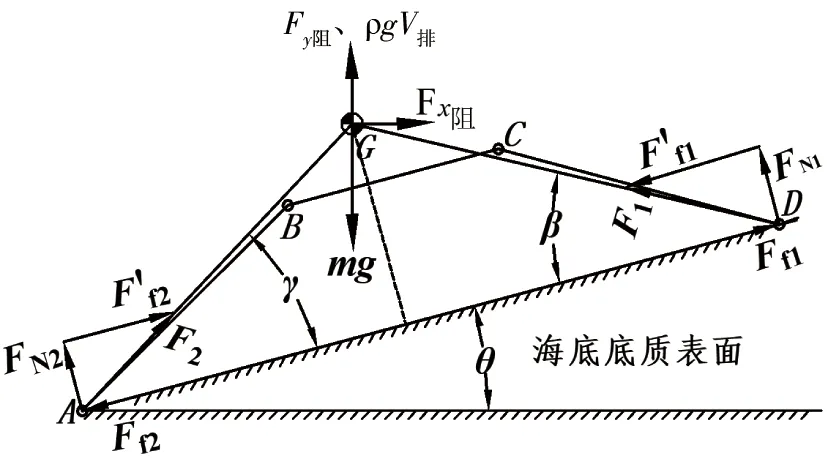
图6 深海海底钻机碰撞受力分析
由图6可知,深海海底钻机碰撞瞬间受力可表示为
(14)
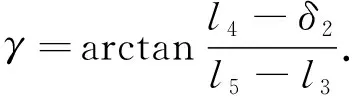
求解式(14)得
(15)
忽略x方向上海底底质的压溃和滑移,对各组支腿进行受力分析可知:
(16)
(17)
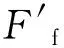
深海海底钻机支腿脚板的摩擦力为
(18)
3 仿真计算及算例
根据已建立的深海海底钻机着底理论模型,建立深海海底钻机着底碰撞模型,利用Matlab软件进行仿真计算,对深海海底钻机着底动力学过程进行仿真模拟与数值求解.针对深海海底钻机着底稳定性控制的相关运动参数,根据姿态角和底质倾角的组合,进行深海海底钻机着底稳定性搜索,得出深海海底钻机的稳定区域.
深海海底钻机稳定域数值计算工况规定如下:确定下落高度h为3 m;底质倾角θ从0°~30°内变化,每次变化间隔为10°;姿态角φ从-40°~40°内变化,每次变化间隔为5°.仿真计算时规定:深海海底钻机姿态角的方向以过质心的垂直轴为基准,顺时针区域为正,逆时针区域为负;海底底质倾角的方向以水平轴为基准,顺时针区域为负,逆时针区域为正.
深海海底钻机动力学仿真参数:转动惯量J为26 800 kg·m2;水下总质量m为8 000 kg;支腿与脚板平面的夹角α为30°;下落高度h为3 m;支腿长度l为2.8 m;两组支腿铰接点(BC)间的距离l1为2.2 m;点E到第1组支腿碰撞点D的距离l3为2.4 m;质心G到AD面的距离l4为2 m;两组支腿碰撞点(AD)之间的距离l5为5 m.
仿真所用的深海海底钻机结构参数数值由本实验室“海牛号”海底多用途钻机测得,其余参数根据深海海底钻机历次实际采样取近似数值.同时,结合宋连清[12]调查所得的海底底质土工资料,选取摩擦因素为0.1,进行稳定域的搜索计算.深海海底钻机着底动力学计算流程如图7所示.
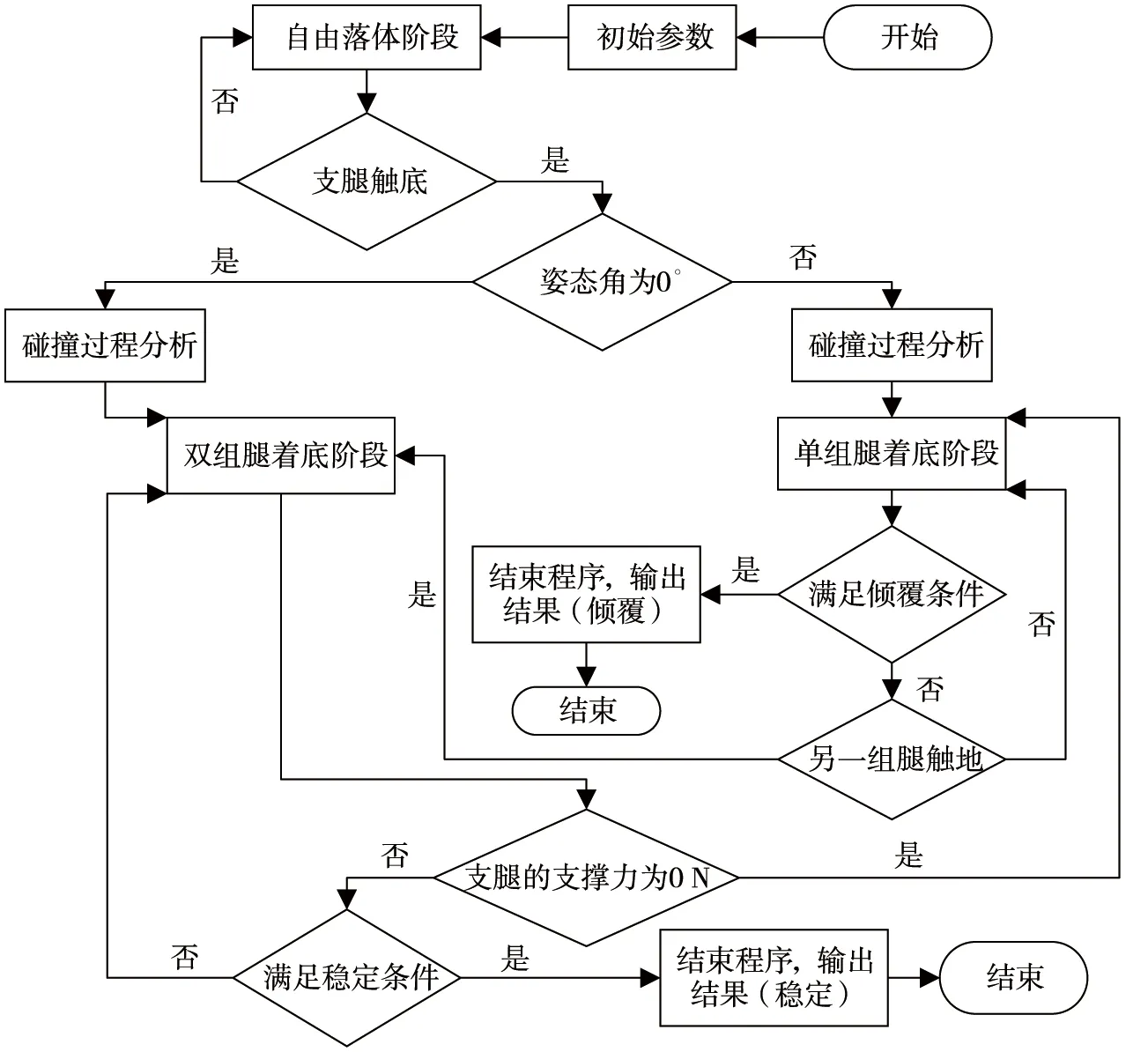
图7 深海海底钻机着底过程动力学流程
现针对深海海底钻机有关初始运动参数,搜索深海海底钻机着底的稳定区域.由于海底洋流速度很小,对深海海底钻机姿态角的影响也很小,因此在搜索稳定域时,只考虑深海海底钻机初始姿态角和海底底质倾角对着底稳定性的影响,不考虑自由落体阶段深海海底钻机姿态角的变化.
以深海海底钻机2-1着底模式为例,对初始姿态角范围(-40°~40°)和海底底质范围(0°~30°)进行着底稳定性搜索,得出如图8所示稳定域图.
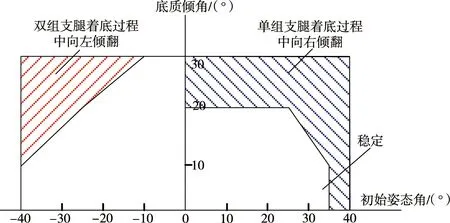
图8 深海海底钻机着底稳定域
由图8可知,2-1着底模式下初始姿态角和海底底质倾角对深海海底钻机着底稳定性都有一定的影响.深海海底钻机在经历单组支腿着底过程时,由于着底支腿数量少、位置分布不均匀等原因更容易发生倾翻,随着海底底质倾角从0°变化至30°、初始姿态角从0°变化至40°过程中,钻机将趋于不稳定,最终向右倾覆;当深海海底钻机单组支腿稳定着底后,钻机将进入双组支腿着底过程,此过程由于着底支腿数量多且支撑面积较大等原因较不易发生倾覆,但随着海底底质倾角从0°变化至30°、初始姿态角从0°变化至-40°过程中,钻机会由于转动角加速度过大而向左倾覆.2-1着底模式下钻机初始姿态角为正值时的稳定范围小于初始姿态角为负值时的稳定范围,为了保证深海海底钻机着底全过程不发生倾覆,建议深海海底钻机着底时初始姿态角不超过±25°,海底底质倾角不超过20°.
为了说明不同初始参数下深海海底钻机着底过程的冲击加速度和稳定性判据随时间的变化规律,对图8中3种典型的着底工况进行动力学分析.
1)仿真算例1.设置深海海底钻机着底动力学过程初始条件:初始姿态角10°,海底底质倾角15°.在此初始着底条件下,深海海底钻机将稳定着底,深海海底钻机着底过程质心加速度和稳定性判据分别如图9和图10所示.
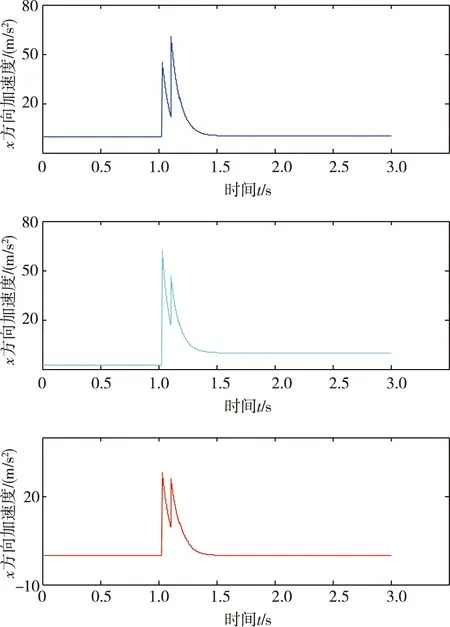
图9 着底过程质心加速度变化
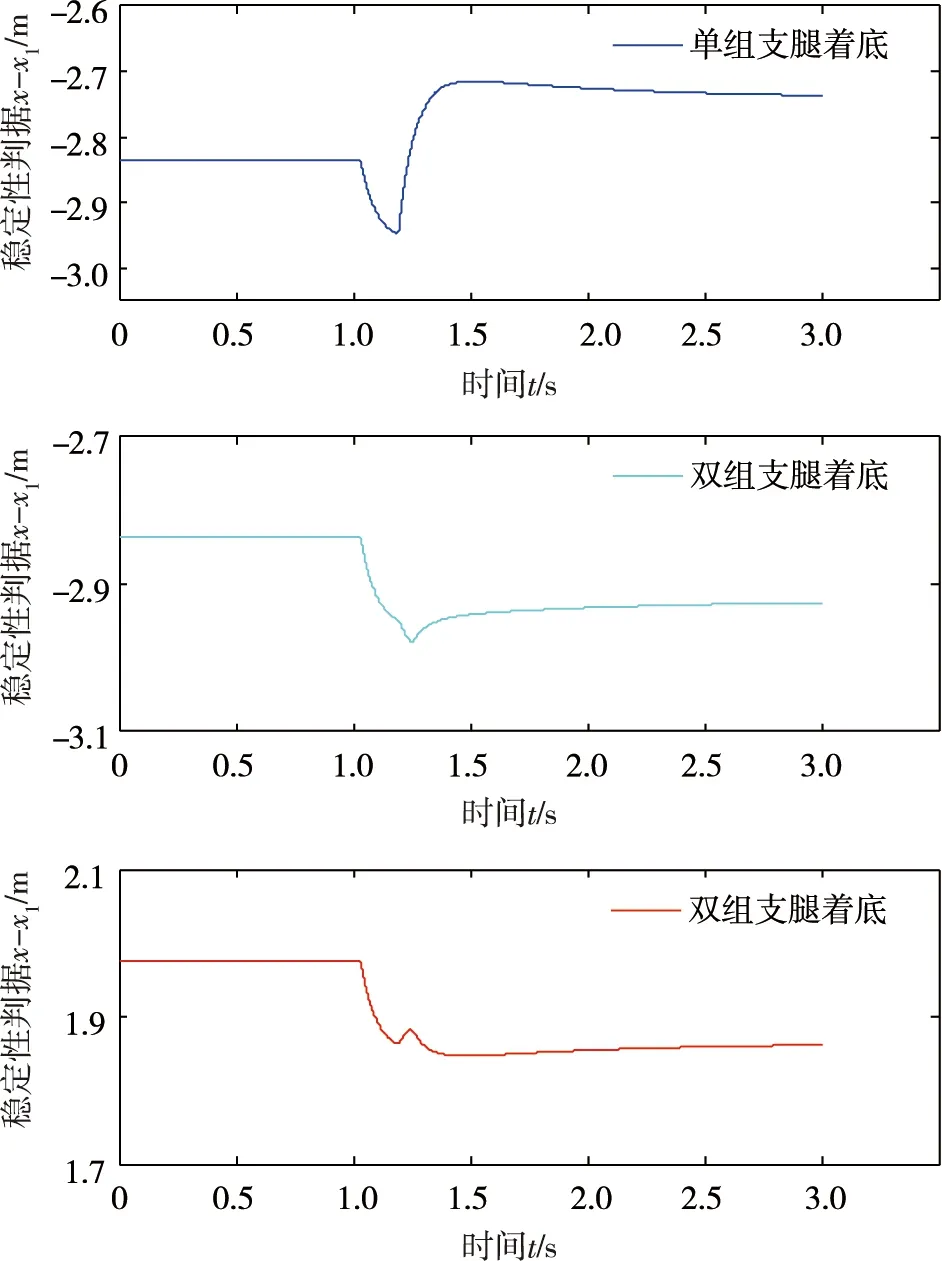
图10 着底过程稳定性判据变化
由图9可知,此工况下深海海底钻机的最大冲击加速度发生在第1组支腿与海底底质在y方向上碰撞时,其值约为6.2g,小于要求值10g,钻机不会发生结构破坏,1.5 s后钻机转动角加速度为0.由图10可知,深海海底钻机单组支腿着底时x-x1<0,双组支腿着底时x-x1<0且x-x2>0,说明在单组支腿着底过程和双组支腿着底过程中深海海底钻机都能保持稳定,不会倾翻.
2)仿真算例2.设置深海海底钻机着底动力学过程初始条件:初始姿态角-30°,海底底质倾角20°.在此初始着底条件下,深海海底钻机将向左倾翻,深海海底钻机着底过程质心加速度和稳定性判据分别如图11和图12所示.
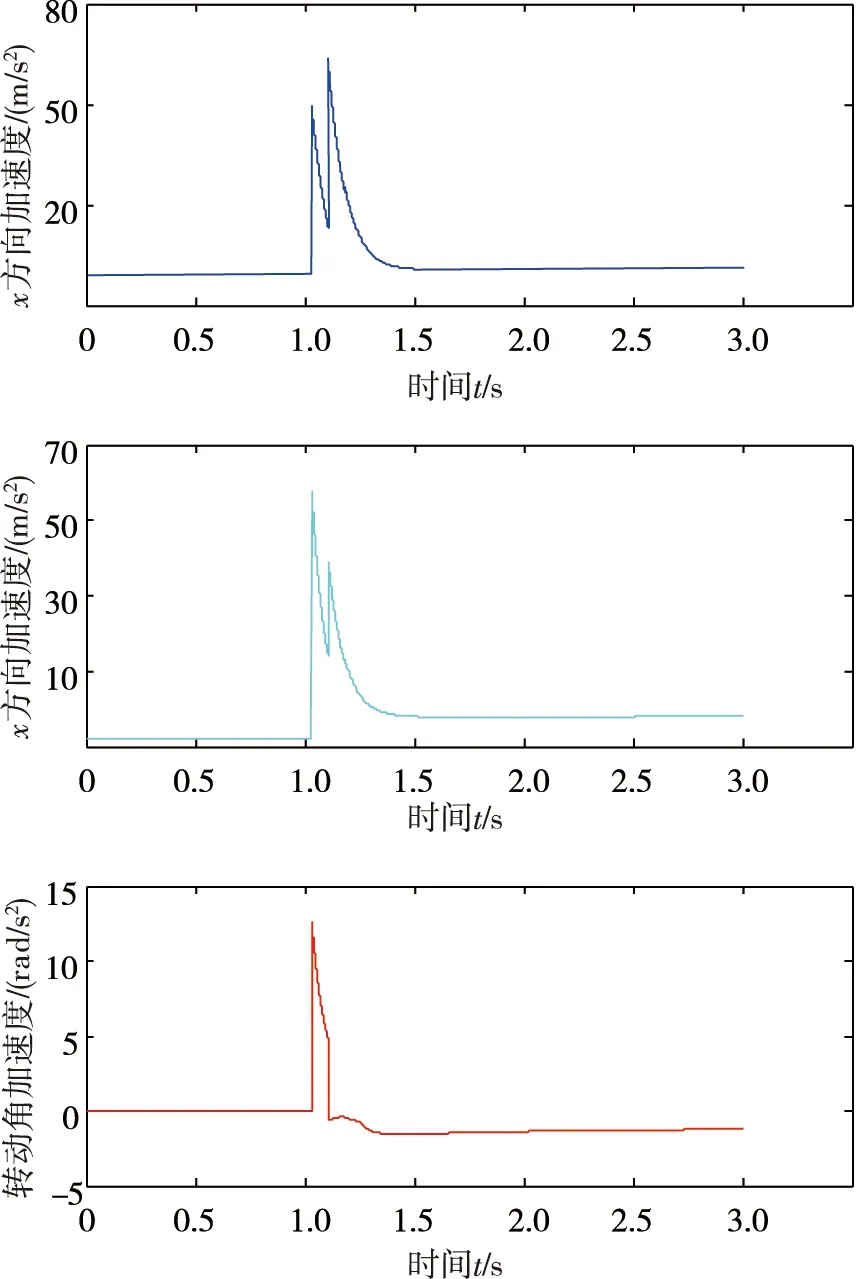
图11 着底过程质心加速度变化
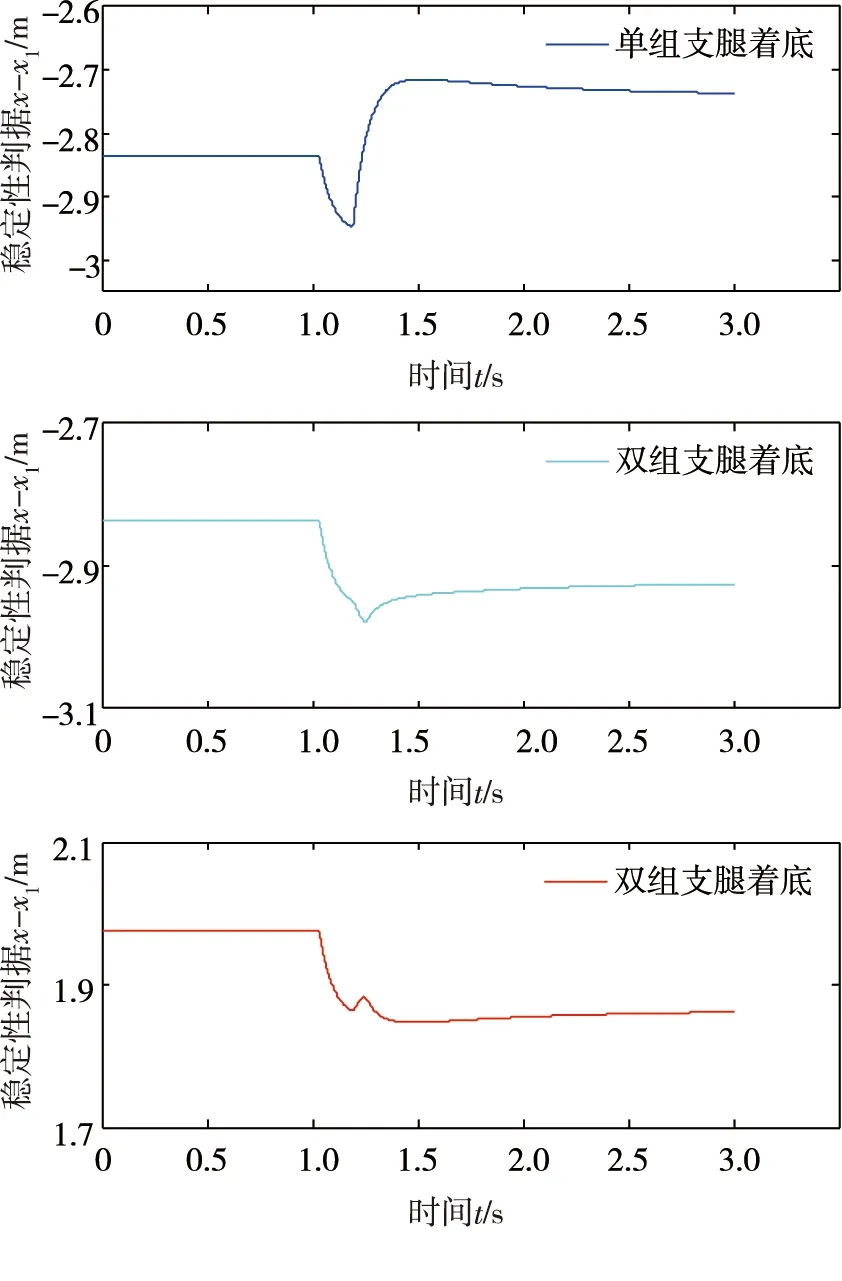
图12 着底过程稳定性判据变化
由图11可知,此工况下深海海底钻机的最大冲击加速度发生在第2组支腿与海底底质在x方向上碰撞时,其值约为6.3g,小于要求值10g,钻机不会发生结构破坏,但由于1.5 s后钻机角加速度仍小于0,此时钻机将继续转动.由图12可知,深海海底钻机单组支腿着底时x-x1<0,双组支腿着底时x-x1<0且x-x2<0,说明在单组支腿着底过程中深海海底钻机能保持稳定;但进入双组支腿着底过程后深海海底钻机不满足支撑稳定性判据,将向左倾翻.
3)仿真算例3.设置深海海底钻机着底动力学过程初始条件:初始姿态角35°,海底底质倾角20°.在此初始着底条件下,深海海底钻机将向右倾翻,深海海底钻机着底过程质心加速度和稳定性判据分别如图13和图14所示.
由图13可知,此工况下深海海底钻机的最大冲击加速度发生在第1组支腿与海底底质在y方向上碰撞时,其值约为5.7g,小于要求值10g,钻机不会发生结构破坏,但由于1.5 s后钻机角加速度仍大于0,此时钻机将继续转动.由图14可知,深海海底钻机单组支腿着底时x-x1<0,说明在单组支腿着底过程中深海海底钻机即将发生向右倾翻,而不会进入双组支腿着底过程,后续双组腿着底过程分析实际上已不存在价值.
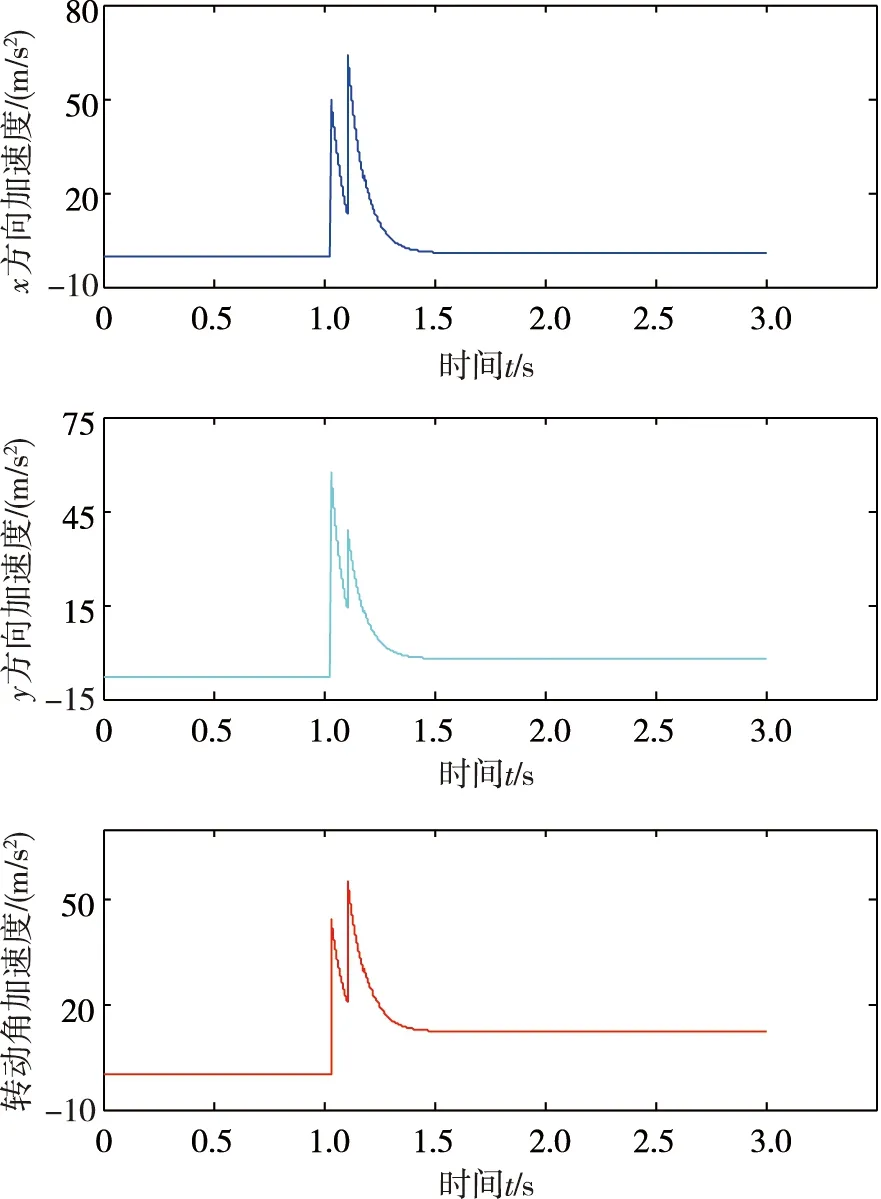
图13 着底过程质心加速度变化
4 结论
1)当着底时初始姿态角不超过±25°、海底底质倾角不超过20°时,3腿支撑式深海海底钻机具有较好的稳定性,不会发生倾覆.
2)当离底下放高度为3 m时,深海海底钻机着底过程中产生的冲击加速度小于10g,能保证深海海底钻机以硬着底方式进行着底而不发生结构损伤和破坏.
