基于温度-渗流-应力耦合作用下地下采空区损伤岩体受力分析

李嘉豪,陈延可,文金萍,夏常宇

(江西工业工程职业技术学院 岩土工程应用技术研究中心,江西 萍乡 337000;江西工业工程职业技术学院 能源工程学院,江西 萍乡 337000)

深部围岩的受力由于受到地应力、温度、地下水渗透及岩石本身损伤等多种因素的影响,比浅部岩体的受力情况要复杂得多,因此,对深部围岩的力学分析和控制技术是近年来研究的热门领域.随着我国的采矿行业发展,越来越多的矿井进入深部开采阶段,随之引起了各种地质灾害,以江西省为例[1],据不完全统计,江西省采空区面积达267.52 km2,形成采空区塌陷面积199.46 km2.因此,如何评价采空区围岩的力学特性是解决空区围岩稳定性的核心问题.

耦合是指2个或2个以上的体系或2种运动形式间通过相互作用而彼此影响以至联合起来的现象.多场耦合作用存在于煤岩体成岩和改造的整个过程,随着煤矿开采深度的增加,地温也将随之增加,煤岩体将受到温度和压力的耦合作用,即热-力耦合作用.而空区内的围岩,受到采动的影响,已经处于损伤状态,不能用原来的岩石力学参数来描述已损伤岩石的力学特性,即呈现出损伤-力耦合的特性.同时,地下采空区多含有积水,水的渗流和渗透将会改变围岩的力学性能,此时的围岩也将受到流-力耦合作用.现实的工程实际中,围岩的力学特性往往受到多个物理场的叠加,如应力场、损伤场、温度场、渗流场、化学场等,而这些物理场之间有时候又是相互影响的.因此我们在分析采空区围岩的力学特性时,不得不面对多场耦合的问题.现在也有越来越多的学者在进行这方面的研究,并取得了一定的成果,如孟宪波,徐佑德等[2],研究了多场耦合作用下储层地应力场的变化规律;柴军瑞,仵彦卿[3]建立了岩体渗流场与应力场耦合作用的多重裂隙网络模型.官兵,李士斌等[4]分析了油气开采过程中水平井压裂的多场耦合应力场.但这些研究大多是基于2场或3场的不完全耦合分析[5-10],并未对模型的数值求解过程进行严密的论证,这对于解决现场复杂的岩体受力显然还不够.本文拟从损伤岩体的角度来分析在温度、渗流和应力耦合下的地下采矿区围岩的力学特征,并建立基于损伤的岩石热-流-应力耦合模型,为解决这类问题提供理论参考和数值模拟依据.

1 深部采空区岩体的受力特征及耦合关系分析

工程实践当中,深部采空区围岩受力是处于多场全耦合的作用下.从温度场角度来讲,温度场对应力场的影响主要表现为岩体内部温度变化时会改变岩石的物理力学性质,某些岩石随温度的升高弹性模量和强度出现衰减,并使其塑性表现得更加明显,同时温度变化会产生热应力作用,使得原应力场发生改变.应力场对温度场的影响主要表现为应力改变岩体结构,进而改变岩体的导热性能.渗流对温度场的影响主要表现为渗流会改变热传导的方式和效率,能促使岩体内热能以对流的方式发生转移,改变其温度场的分布,同时岩体温度的变化,会改变岩石和流体的热物理性能和结构特征,从而影响岩石的渗透性,使得渗流场发生改变.岩体中渗流对应力的耦合作用主要通过地下水的流动来实现,当岩体中有渗流发生时,会引起渗流作用力,其中包括静水压力和动水压力,将改变岩体中原来的应力场分布,岩体中应力的改变,又将影响岩体的结构,从而改变岩体的渗透性能,主要表现为改变渗透系数[8-10].

岩体损伤和各场的耦合作用主要表现[11,12]:损伤岩体的力学参数将被劣化,进而影响岩体的力学特征和内应力场的分布;损伤将使岩体的孔隙率增加,进而影响流体的渗透率,同时通过流体的渗透改变热传导的方式,提高了耦合介质的热传导率;其次,岩体损伤过程中有部分机械能会转化为热能,引起温度的局部增高.而同时应力场、渗流场和温度场又会影响岩体的断裂形式和裂纹分布,渗透压力和温度应力将进一步引起岩石的损伤.

若考虑煤矿深部采空区岩体内还积聚着各类有毒有害气体,则采空区岩体还存在着气-固耦合关系.在采用灌浆处理过的采空区内,还会存在着化学场的耦合作用.但在研究各场耦合的过程中,有些耦合作用比较明显,并且对应力场的分布和研究的目标产生较大的影响,我们称之为强耦合作用,如温度的升高会产生膨胀应力,渗流过程中有渗透压力等,这些耦合会较大程度引起应力场的变化.而岩体破裂虽然会引起温度的局部升高,但温度局部升高对应力场、温度场和渗流场的影响都不明显,为弱耦合作用.

2 岩体热-水-力-损伤(THMD)耦合数值模型的建立

2.1 耦合机制模型

根据上述分析,采空区岩体事实上处在温度-渗流-损伤-应力的(THDM)全耦合作用下.在这些耦合作用当中有强有弱,根据本研究的对象和目的,也为了研究的可行性,本文忽略某些弱耦合作用以及其他诸如气-固耦合、化学场耦合等对地下采空区围岩影响不太明显的因素,建立一种基于THDM的非全耦合的作用机制,以此建立各物理场的控制方程.所考虑的耦合关系如图1所示,图1中实线表示考虑的强耦合作用,虚线为不考虑的弱耦合作用.

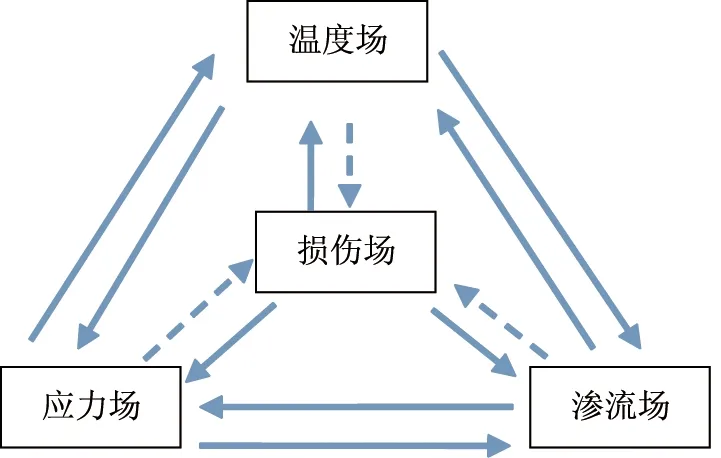
图1 THMD耦合作用机制

2.2 力学模型

根据图1的耦合作用模型,建立各场控制方程.

2.2.1 应力场控制方程

控制方程是耦合模型的关键,各场控制方程都应考虑其与物理场的耦合影响,才能体现出耦合的作用.根据上述的耦合机制模型,并考虑孔隙渗透水压力、温度应力、损伤后岩石力学参数弱化的影响,在文献[5]的基础上,建立本构方程为

(1)

其中，

(2)

(3)

(4)

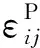
2.2.2 应力场平衡方程

考虑到耦合过程是一个复杂的动态平衡过程,因此采用弹性力学平衡方程中的运动微分方程:

(5)

式中:σij,j为总应力在i方向上的分量;ρ为多项耦合的围岩密度,kg/m3;Fi为岩石介质的体积力分量;vi为i方向上的速度;t为时间.当围岩处于静力平衡时,式(5)右边等于0.

根据式(1)和式(5),平衡方程可改写为

(6)

2.2.3 基于应力-渗流-温度相互耦合的温度场控制方程

根据第一部分的分析,考虑损伤对温度场影响,在文献[6-8]的基础上,本文提出的温度场控制方程可表述为

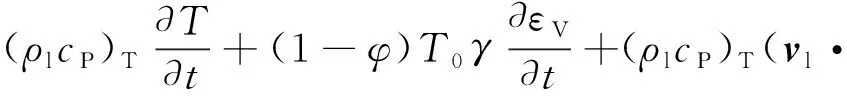
(7)

εV=εx+εy+εz；

(8)

γ=(2μτ+3λ)β1.

(9)

式中:ρl为流体密度,kg/m3;cP为岩体比热容,J/(kg·℃);(ρlcP)T为等效比热容,J/(m3·℃);φ为岩石的孔隙率,是损伤变量D的函数,%;γ为线性膨胀系数;εx,εy,εz分别为x,y,z方向上的应变;vl为流体速度矢量,m/s;KT为充满流体的多孔介质的热传导系数,为损伤变量D的函数,W/(m3·℃);qT为体积热源强度,W/m3;μτ为岩体的拉梅第二系数,J/m3;β1为各向同性固体热膨胀系数,℃-1;.

2.2.4 基于应力-温度-渗流的渗流场控制方程

假设固体基质和孔隙流体处于热平衡状态,根据流体的质量守恒方程和Darcy定律有[9]

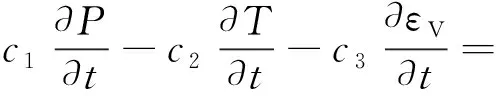
(10)

(11)

(12)

(13)

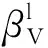
3 岩体损伤对各物理场的影响

损伤岩体在受到力学、温度和渗流作用的影响下,会使得岩体本身和地下水的各项物理力学性质发生变化,其中主要影响岩体的渗透率、孔隙度、压缩系数、地下水密度、运动黏性系数、弹性模量等一系列指标,文献[10]中对他们之间的变化关系做了相关的研究,本文不再论述.

3.1 损伤对渗流场和应力场的影响

损伤对渗流及应力的影响主要表现为对渗透率和孔隙率的影响,损伤会使岩体的渗透率和孔隙率发生明显的改变,而这种影响又和应力形成耦合关系,孔隙率和应力的关系可表述为[11]

(14)

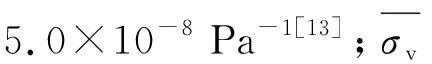
(15)

式中:σ1，σ2，σ3为3个主应力,MPa;α为Biot系数.

渗透率和孔隙率之间的关系可认为满足关系:

(16)

式中:η0为无应力状态下的渗透率,mD.

当岩石损伤后,损伤和岩石的孔隙率和渗透率是相互耦合的,其演化规律相当复杂,本文基于损伤力学和相关研究成果[9,10,13],认为损伤对渗透率的影响关系为

η=(η/η0)3exp(αηD).

(17)

式中:αη为损伤对渗透率的影响系数,取αη=5.0.

3.2 损伤对温度场的影响

损伤对于温度场的影响主要表现为对热传导系数和热容的影响,目前还未见有统一的认识,但损伤必然会引起岩体介质的热导系数升高,基于对模型数值计算时的闭合性考虑,本文假定损伤对热传导系数产生的影响满足指数关系[9]:

KT=KT0exp(D/αk).

(18)

式中:KT0为多孔介质相同温度下受损前的热传导系数;αk为损伤对热导系数的影响系数,可通过实验求得或取经验值.

3.3 损伤对岩石弹性模量和剪切模量的影响

基于采空区岩石已受过采动影响,并且经历过了一次应力释放的过程,故视采空区岩石为弹性体,按照弹性损伤理论,单元体的弹性模量及剪切模量表示为

E=(1-D)E0;

(19)

G=E/[2(1+υ1)]=(1-D)E0/[2(1+υ1)].

(20)

式中:E为弹性模量,MPa;υ1为岩体泊松比;E0为未损伤时的弹性模量,MPa;.

3.4 损伤变量的求取

目前对损伤变量D的求取有多种方法,其中比较被接受的方法有基于连续因子求取、基于应变等效原理求取和基于统计损伤理论求取[11,12,14],也有学者[15]取他们的加权平均值进行计算.

基于连续因子和应变等效原理定义的损伤变量D1可表示为[15]

(21)

式中:σ为作用在损伤材料上的名义应力,MPa;σ′为作用在无损材料上的有效应力,MPa;σ″为作用在损伤材料上的有效应力,MPa.

若微元体未损伤部分服从广义胡克定律,且在只产生轴向损伤的前提下,其损伤模型可表示为[16]

σ1=E0ε(1-D1)+[σr-υ0(σ2+σ3)]D1+υ0(σ2+σ3).

(22)

式中:ε为轴向应变;σr为岩体的残余强度,MPa;υ0为岩体的无损泊松比.

由式(22)整理得

(23)

基于统计损伤理论定义的损伤变量D2目前被大多数学者所认同,其表达式为[17]

(24)

式中:m,ω分别为Weibull分布的形状参数和尺度[18].

本文基于地下采空区岩体的特征,拟采用D1,D2的加权平均值作为损伤变量,则有

(25)

4 基于损伤岩体的温度-渗流-应力耦合方程

根据上述分析,可得在图1的耦合作用机制下,耦合的控制方程组为

(26)

将式(14),式(17),式(18),式(25)分别代入相应的控制方程中,并对方程中的其他参数通过经验或实验进行赋值,就可对方程组进行求解.

5 结论

1)深部矿井采空区岩体的受力是处在多场耦合的作用机制中,不能忽视渗流、温度及损伤对应力场的影响.

2)分析讨论了损伤对各场的影响,并给出了具体表达式,为分析和研究损伤问题提供了理论参考.

3)考虑了损伤场的影响,给出了基于损伤的4场耦合表达式,为数值模型的实现奠定了基础.