大型有限元模型频响快速修正方法
2021-07-14范新亮张丽君夏遵平
范新亮, 王 彤, 张丽君, 夏遵平
(1. 南京航空航天大学 机械结构力学及控制国家重点实验室, 南京 210016;2. 中车唐山机车车辆有限公司, 唐山 063000)
有限元模型修正首先在航空航天领域提出,发展至今日已形成了一个庞大的理论体系,并且在运载火箭、卫星、航天飞机、飞机和直升机结构的响应与载荷预示、颤振分析、振动控制均得到了广泛的应用[1]。模型修正方法按用以修正的试验数据不同可分为基于模态参数的方法[2-6]和基于频响函数的方法[7-9]。Modak等[10-11]通过数值仿真详细对比了两种方法的差异及收敛性。基于模态参数的方法易受模态识别的影响而引入了误差及不确定性;而基于频响函数的方法则避免了提取模态参数带来的误差,且具有大量数据,对于解决待修正参数众多的问题具有优势。然而,在大噪声干扰下和初始频响残差较大时收敛困难、规模庞大的有限元模型修正效率低下等问题均制约着基于频响函数的模型修正方法的进一步发展。
为了提高频域修正方法的收敛性,Pascual等[12-13]基于频响相关性准则,提出一种移频方法,并利用分析和测试频响相匹配的频率点对应数据进行修正,提高了参数的收敛速度及范围。Gang等[14]在该方法基础上引入伪自由度的概念解决测试频响信息不足而导致收敛困难的问题。为了解决自由度数目庞大的有限元模型修正问题,常常需要引入模型缩聚方法将有限元自由度缩聚至测试自由度。而利用模型缩聚难以避免引入较大的近似误差,Li等[15]通过迭代过程更新缩聚矩阵来减小缩聚引起的误差。模型缩聚方法仅可利用测试自由度上的频响信息的特点不利于收敛,Gang等提出将有限元模型缩聚到实测和用户选择的伪自由度上,从而增加了用于修正的频响的自由度数目。但是利用模型缩聚的坐标缩减方法引起的误差依旧较大,且形成缩聚矩阵本身计算量也较大。因此又有学者研究了采用子结构综合技术对系统的自由度缩减后进行模型修正的方法。Papadimitriou等[16]在贝叶斯模型修正技术的基础上,利用模态综合技术得到缩减的系统,并计算相应的灵敏度,减小了修正的计算规模。王陶等[17]提出了基于改进自由界面子结构模态综合法的结构模型修正方法,通过子结构综合技术得到由摄动量表示的综合系统方程和灵敏度方程,仅需对综合方程进行修正。然而对于频响函数在综合坐标下的灵敏度以及如何对频域的系统缩减后进行模型修正的方法尚少有研究。
为此,本文提出一种基于缩减基的有限元模型频响修正方法,将系统的位移表示为模态综合缩减基或模态振型缩减基的线性叠加,从而将自然坐标映射至缩减坐标下,得到了缩减坐标下的频响函数残差的灵敏度矩阵,使得修正过程均在缩减坐标上进行,相比利用模型缩聚将总体自由度映射至测试自由度上的方法,在计算效率及精度上均有所提高。同时引入移频方法以增加收敛性,由原先的基于测试频响的频率点处的频响残差最小化改进为基于所匹配的频率点处的频响残差最小化;并基于模态展开式推导了精度较高的分段频响扩充方法,减小扩充误差对修正过程的影响。仿真算例和试验验证均表明该方法对于规模巨大的有限元模型能高效地得到稳健的修正结果。
1 理论背景
1.1 模态综合方法
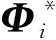

图1 薄板模型子结构划分
(1)
根据界面协调条件可得到系统自然坐标下的总体位移向量u为
(2)
其中Bs为子结构的约束模态集及主模态集所组成的Φ经坐标变换矩阵T、S作用后的综合基
Bs=TΦS
(3)
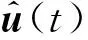
(4)
式中,M、K、C、f分别为质量矩阵、刚度矩阵、阻尼矩阵、载荷向量。式(2)代入式(4)推导得到系统在模态综合坐标下的运动方程为
(5)
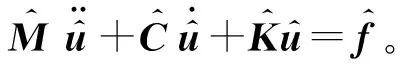
1.2 基于模态综合缩减基的修正方法
假设系统的真实参数为p*,对应系统矩阵分别为MT、KT、CT,由式(5)在综合坐标下有频域公式
(6)

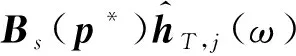
类似地,假设有限元模型的初始参数为p,有:
(7)
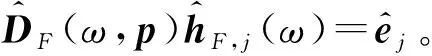
(8)
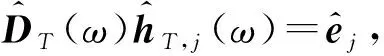
(9)
取DT=DF+ΔD代入式(8),其中ΔD为动刚度矩阵的修正量可得到
(10)
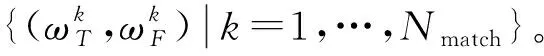
与文献[14]类似,可推导得到进行频率点匹配后的迭代修正方程

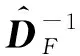
(11)

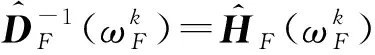
(12)
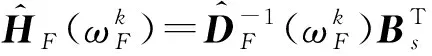
(13)

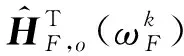
(14)
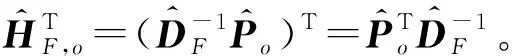
假设有限元模型按材料参数分为Np个组,则可以将ΔD(ω)表示为
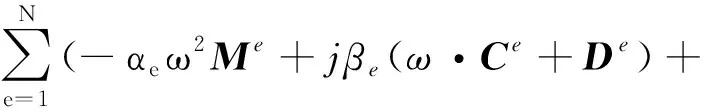
γeKe)
其中:Me、Ke为单元质量、刚度矩阵,αe、γe为单元质量、刚度矩阵修正系数增量;Ce、De为单元阻尼矩阵,βe为单元阻尼矩阵修正系数。将该式代入式(14)可得到系统参数识别方程
(15)
其中θ为αe、βe、γe组成的待识别的修正参数增量,系数矩阵S为
(16)


(17)
式(15)即为利用模态综合缩减基转换至模态综合坐标下的频域模型修正公式。

1.3 基于模态振型缩减基的修正方法
由频响模态展开式
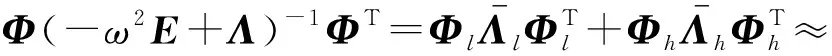
(18)
式中:Φ为系统的模态振型;Λ为系统特征值;E为单位矩阵;下标l与h分别代表系统的低阶模态与高阶模态。将式(18)右乘ej并展开得到
(19)
由式(19)知任意一列频响可通过系统的模态振型叠加而得。即测试频响可以用实际系统的完备低阶模态作为基底进行表示。而实际系统的完备低阶模态无法得到,因此以有限元模型的完备低阶模态进行代替。由式(19),取拟合式
(20)
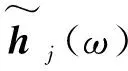
(21)
其中上标*表示测试自由度对应分量,由式(20)、(21)得到扩充后测试频响
(22)
与式(19)类似,取测试频响及有限元频响为
(23)

自然坐标下基于移频的频响直接矩阵方法的公式为
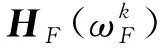
(24)
式(23)代入式(24)简化得到

(25)

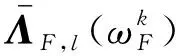
(26)

式(26)即为利用模态振型缩减基转换至模态坐标下的频域模型修正公式,与式(14)形式一致,通过1.2节类似推导可得其迭代方程。将基于模态综合缩减基或模态振型缩减基的方法统称为缩减基方法。
1.4 算法实现相关问题
1.4.1 缩减基与模型缩聚的对比
应用最广泛的IRS缩聚(improved reduced system)方法,其缩聚矩阵为[18]
(27)

对于1.3节中转换至模态坐标下和通过模型缩聚转换至测试坐标下的修正方法,可以分别理解为以有限元模型的低阶模态矩阵ΦF,l和特定的缩聚方法得到的基Td代替式(2)中的模态综合基矩阵Bs,而后进行与1.2节相同的推导得到与式(15)形式完全相同的修正公式,即
(28)
(29)

值得注意的是,三种方法无一例外需要以有限元模型的基矩阵代替相应真实系统的基矩阵,带来了近似误差,因此三种基矩阵在近似误差的差异上的比较也成为判断其优劣的标准。虽在数学上难以证明,但在实际应用中发现多数情形下基于模态综合缩减基或模态振型缩减基的方法的近似误差要小于模型缩聚方法,尤其当测点较少时,模型缩聚方法的误差会急剧增加。以某模型为例,图2表示分别以三种有限元基矩阵代替真实系统的基矩阵所形成的坐标下动刚度矩阵求解的频响与真实系统的理论频响的幅值相关性。可见相同情况下,基于缩减基的方法的近似误差要远小于模型缩聚方法。
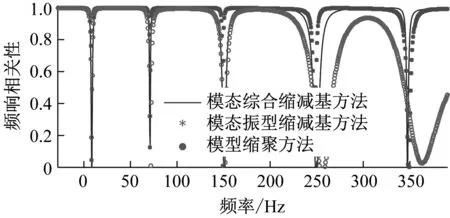
图2 三种方法所计算频响与理论频响幅值相关性对比
1.4.2 基矩阵的迭代更新
subject topL≤p≤pU
(30)

根据上一小节的分析,以有限元模型的基矩阵代替真实系统的基矩阵将带来近似误差。文献[15]通过迭代中不断更新缩聚矩阵Td的方法减小了模型缩聚方法中该误差对待修正参数识别的影响。因此本文方法中每一个迭代步以上一步修正后的有限元模型更新的缩减基矩阵来代替真实系统的基矩阵,随着有限元模型参数逼近真实参数时,该近似误差得以消除。
1.4.3 宽频带频响扩充方法
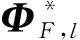
如图3所示,通过选择模态指示函数的半功率带宽内的频率点可以得到测试频响函数的分段:

图3 测试频响函数分段
(31)
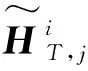
(32)
2 算例分析
2.1 仿真算例
采用Garteur飞机仿真模型验证本文方法的收敛性及迭代速度。有限元模型划分为5个区域,如图4所示。每个区域的弹性模量、密度及阻尼系数作为待修正参数,共计15个参数。分别在无噪声和20%噪声水平下采用本文方法进行修正。有限元模型划分为3个子结构进行模态综合。自然坐标下模型的自由度为99 798,模态综合坐标下模型自由度仅为582,有效减小了修正过程的矩阵运算规模。
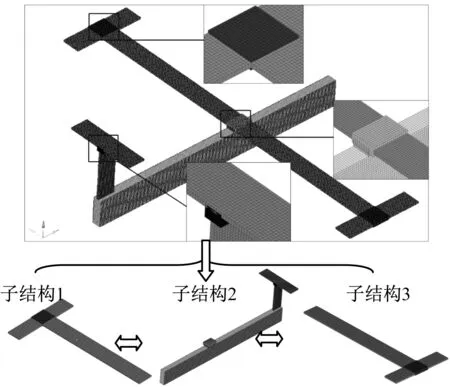
图4 Garteur飞机有限元模型子结构划分
2.1.1 无噪声下频响修正
将待修正参数向量的某组数值作为真实参数值,计算其有限元模型频响作为仿真测试频响;取上下界为真实参数值70%~130%的变化范围对该组数值进行摄动得到有限元模型修正前的初始参数,计算其频响得到初始分析频响。初始分析频响与仿真测试频响对比如图5所示,其相关性较小,残差较大。
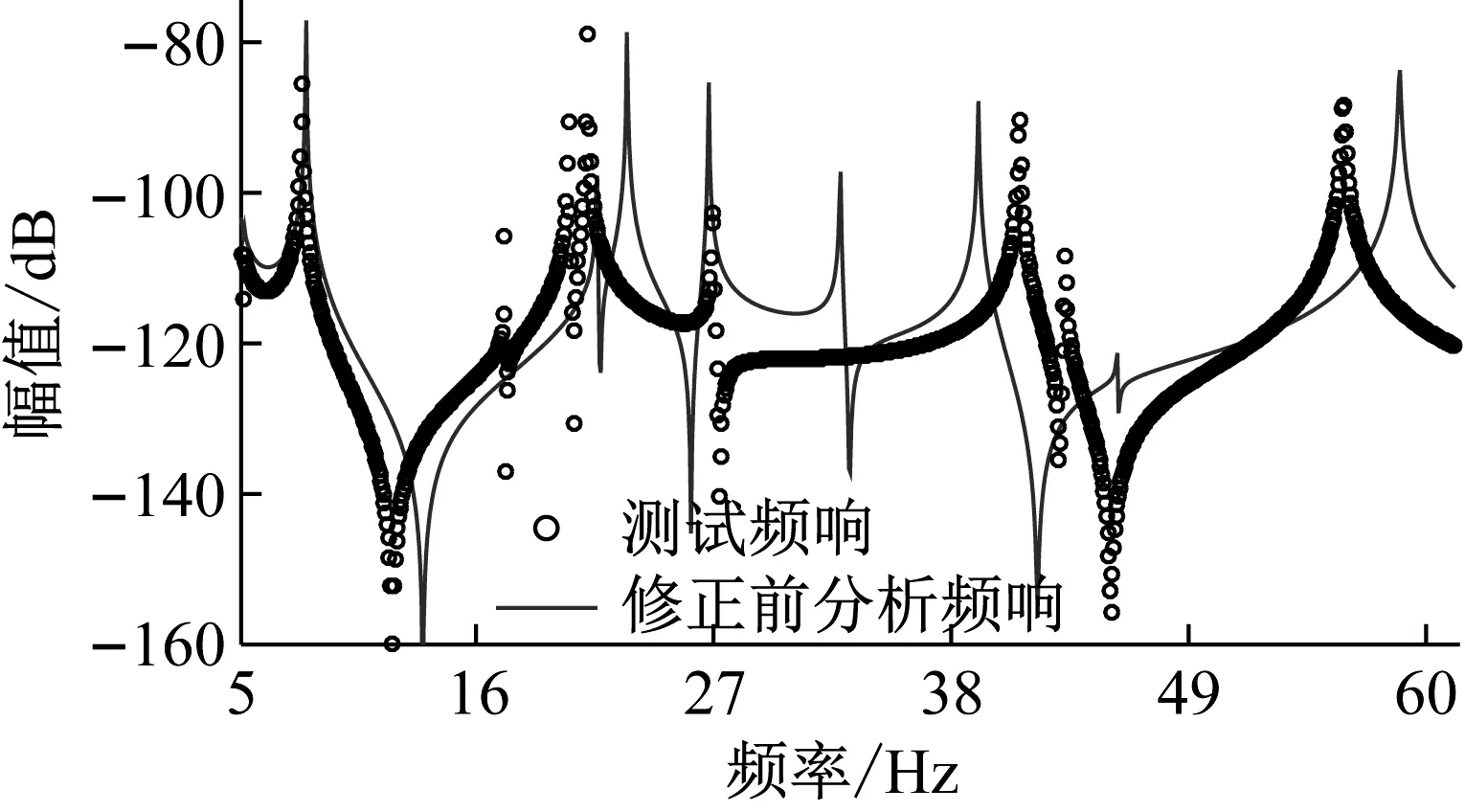
图5 修正前初始分析频响与测试频响对比
如图6、图7所示为经过3个迭代步修正后的分析频响与测试频响,相关性有了很好的改善。理论上在无噪声情形下修正后的参数将与真实参数完全一致,但由于扩充频响过程产生的误差、自由度缩减过程的假设带来的误差是等效的频响噪声,对参数识别的过程同样产生了扰动。在模态综合坐标下,单个迭代步运行时间仅为220 s左右;而自然坐标下则需要2 400 s(硬件信息:CPU-Intel i5 7300HQ,RAM-8G,OS-Windows 10 Pro,SSD-intel 256 G)。可见基于模态综合缩减基的方法在保证参数收敛性的前提下,有效提高了模型修正的效率。
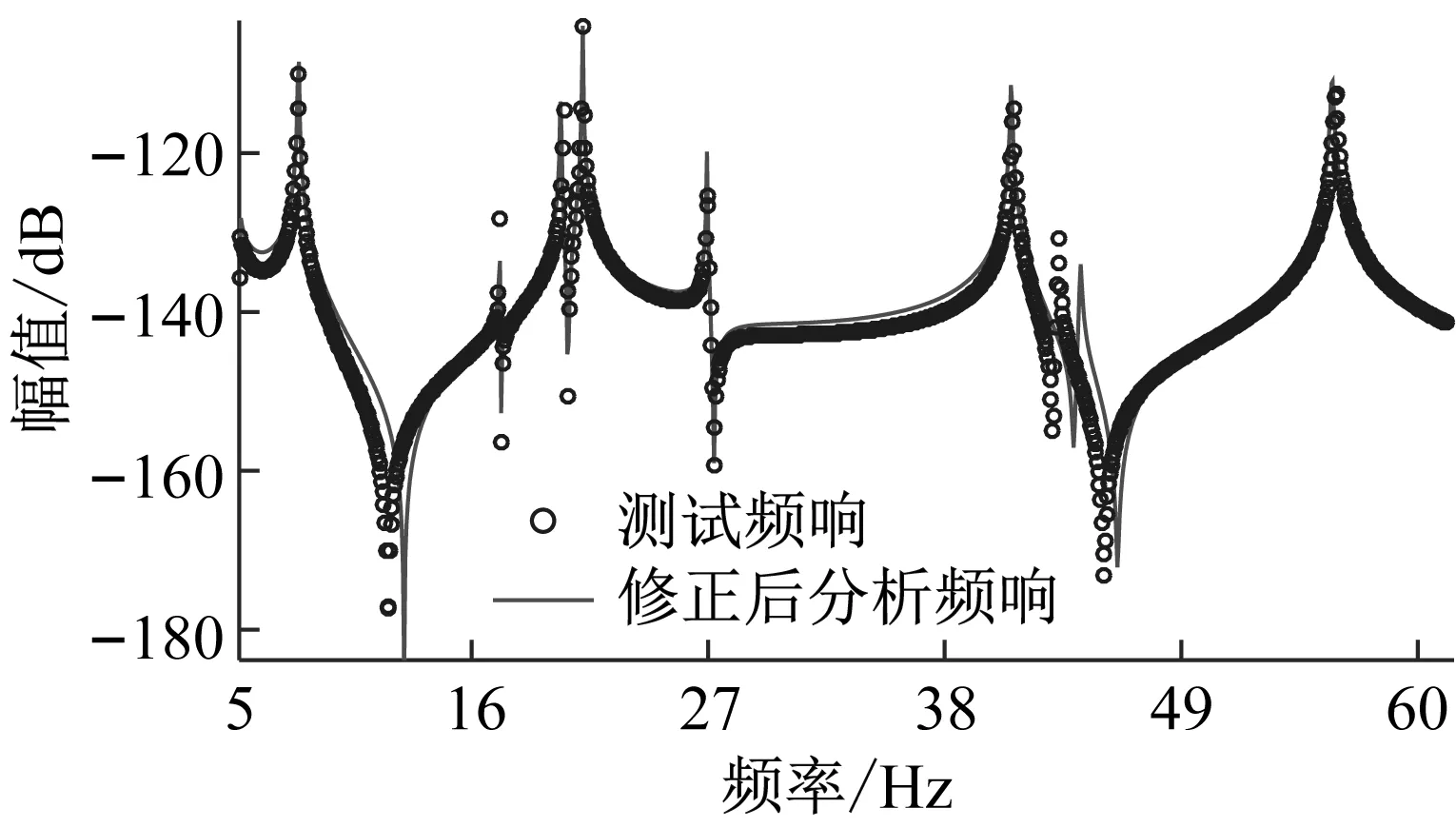
图6 修正后分析频响与测试频响对比
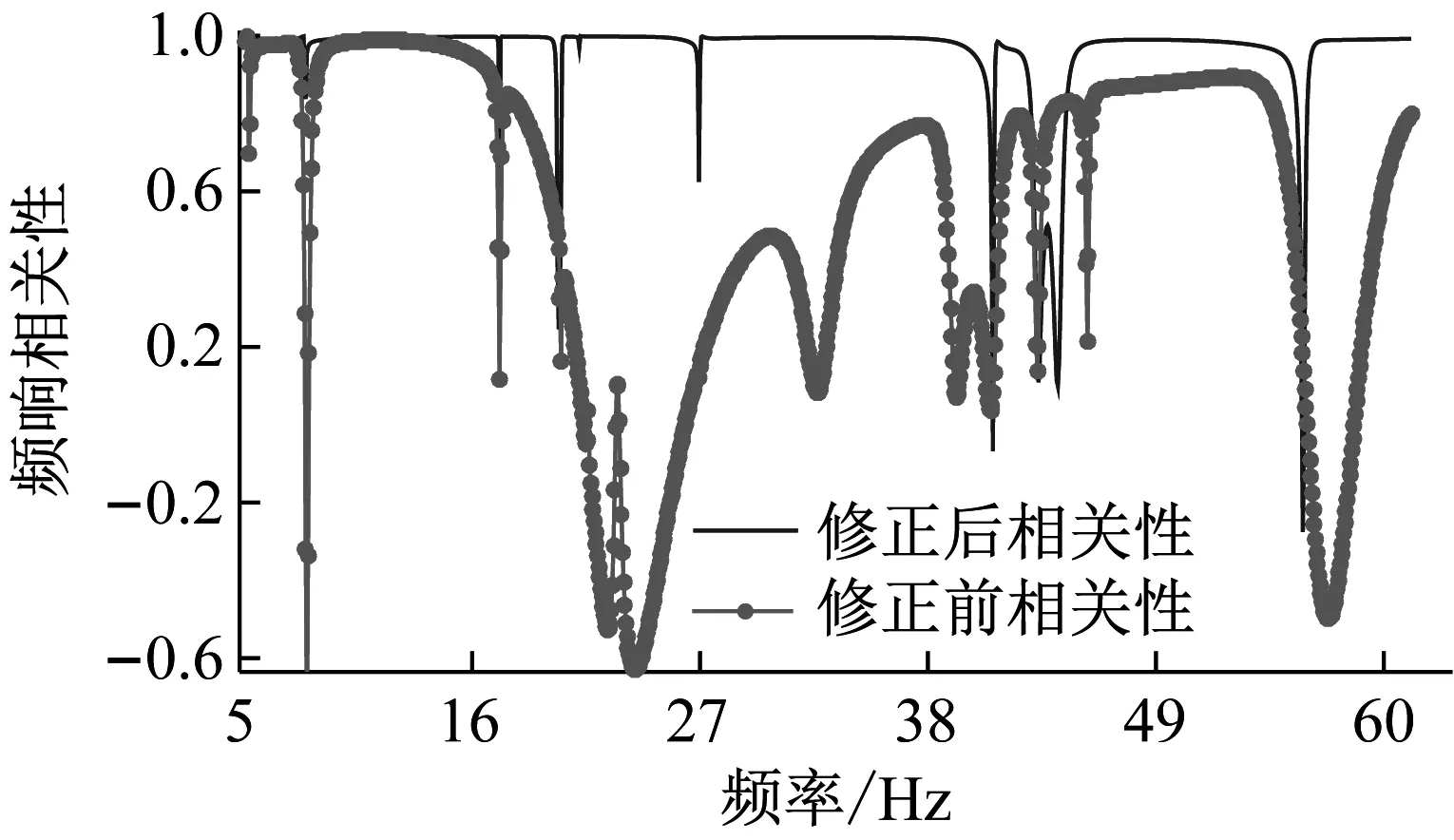
图7 修正前后分析频响与理论测试频响幅值相关性对比
2.1.2 20%噪声水平下频响修正
初始待修正参数设置同2.1.1节。如图8所示,仿真测试频响添加20%的噪声,以验证基于模态综合缩减基的方法在大噪声情形下的修正精度。
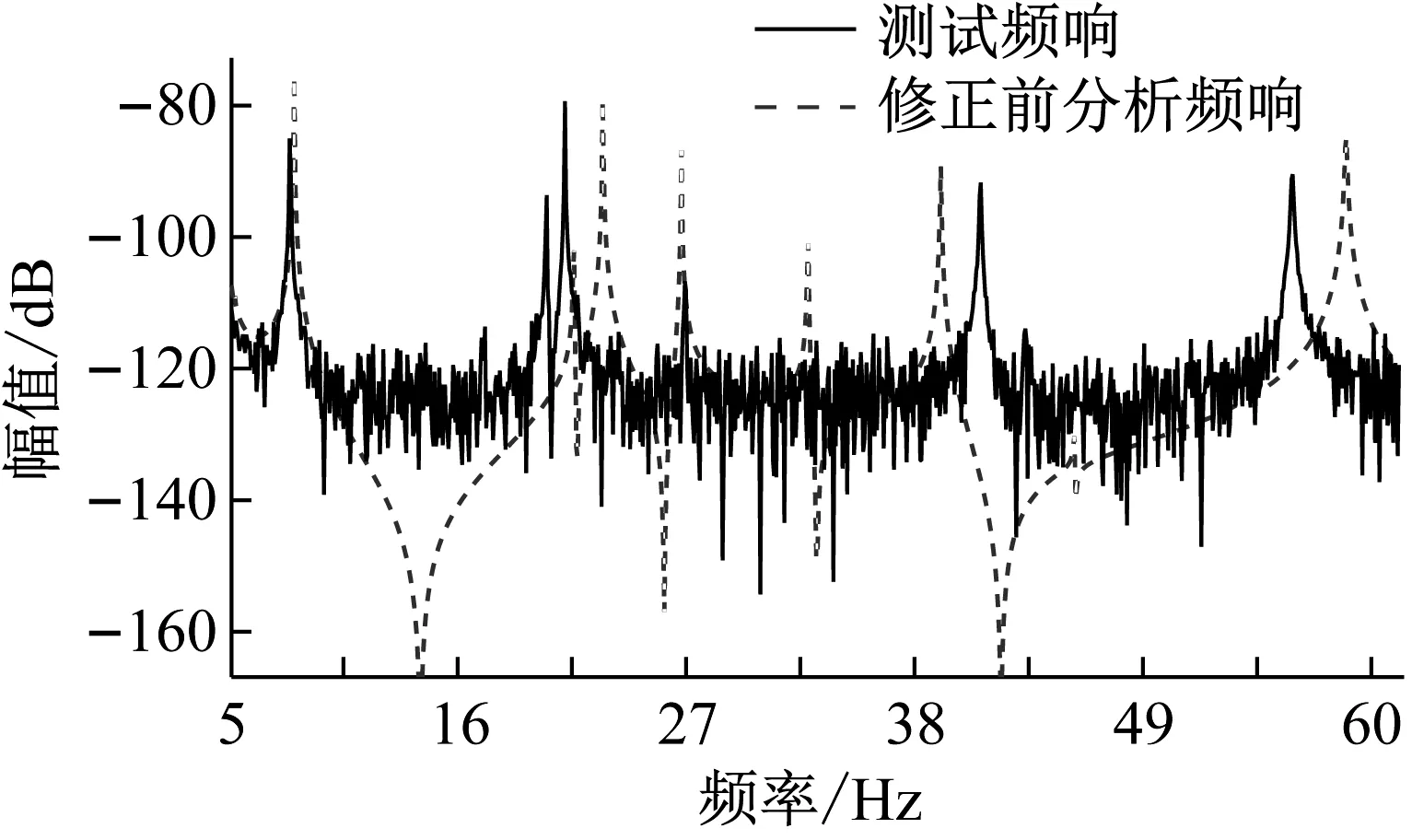
图8 修正前初始分析频响与测试频响对比
在大噪声情形下,经过10个迭代步修正后达到收敛,除第6阶模态对应频带外,其余频带的修正后分析频响与测试频响相关性有了很好的改善,如图9、图10所示。可见在大噪声干扰下,基于模态综合缩减基的方法收敛性仍较好。若采用基于模态振型缩减基的方法,取80阶有限元模态作为坐标变换基矩阵,模态坐标下模型自由度为80,单步迭代所需时间仅为180秒,且修正精度与基于模态综合缩减基的方法类似。
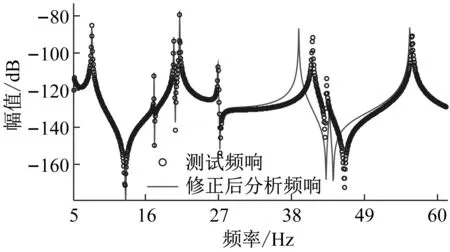
图9 修正后分析频响与测试频响对比
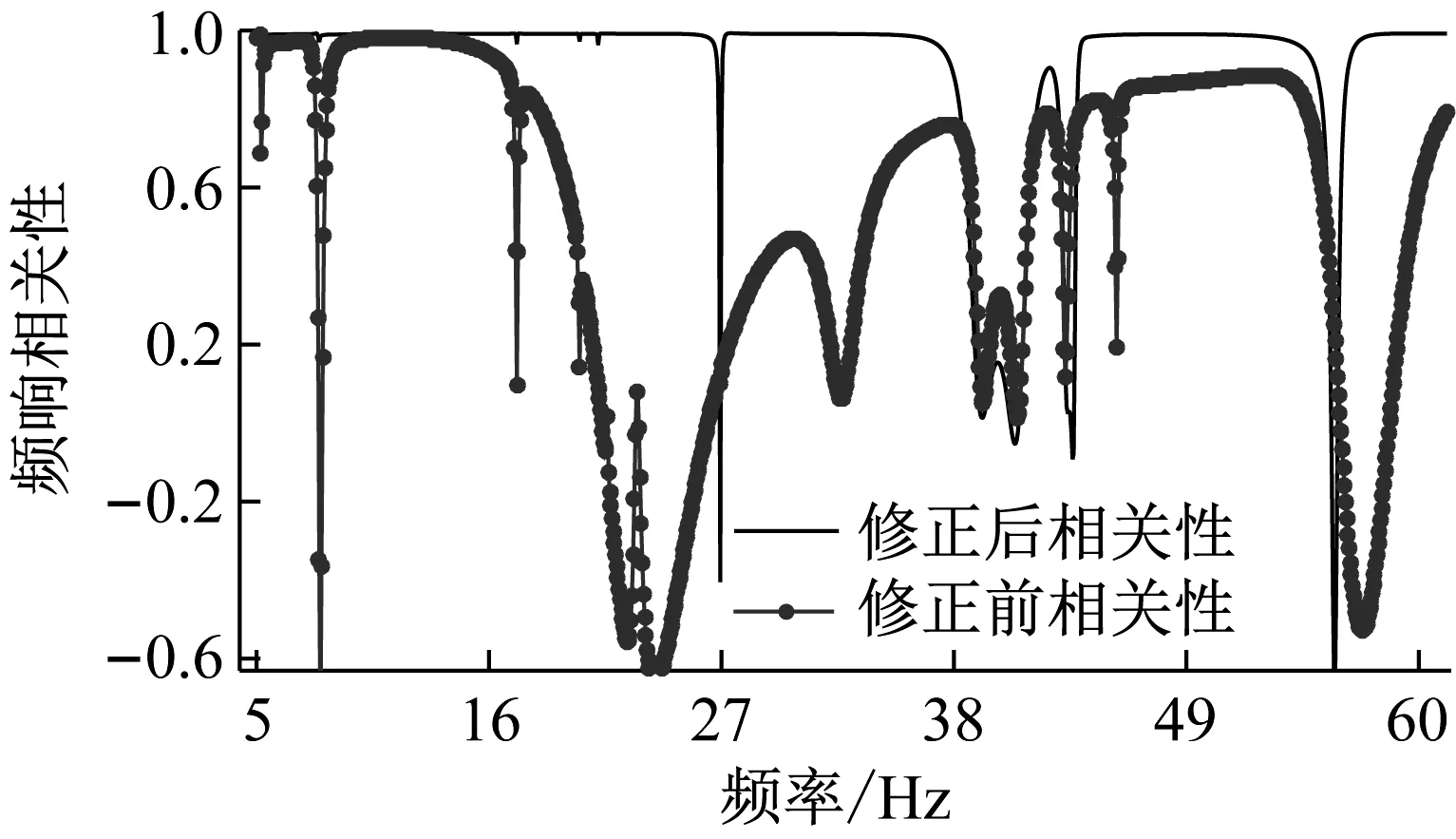
图10 修正前后分析频响与理论测试频响幅值相关性对比
2.2 试 验
以某型列车转向架构架作为试验对象,进行多参考点锤击试验,采用N-Modal模态参数识别软件识别试验结果。从测试角度,测点布置应清晰地反映出各阶振动形态,参考点布置需要考虑到避开各阶振型的节点;从模型修正角度,布置尽可能完备的测点不仅能有效提高扩充精度,且能有效反映有限元模型与测试模型的振动形态差异,所修正的有限元模型亦愈逼近真实模型。如图11所示。

图11 试验结构与测试设备
有限元模型划分为10个区域,如图12所示。每个区域的弹性模量、密度及阻尼系数作为待修正参数,共计30个参数。由于构架为焊接的一体化结构,其各个区域之间焊缝厚度的不确定性以及焊接区域的力学性质的未知导致了有限元模型与实际结构相差较大。同时,数目众多的待修正参数均给模型修正带来了较大的难度。设置初始待修正参数后计算得到初始分析频响,其中某些测试自由度的初始分析频响与测试频响对比如图13所示,其频响相关性较小。
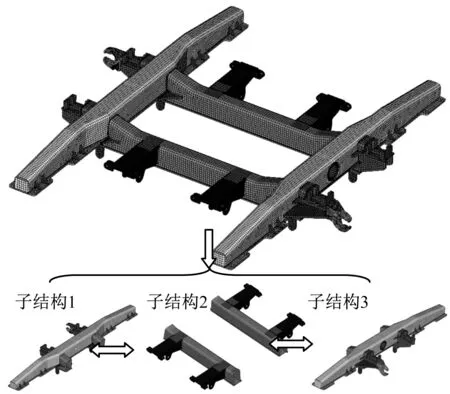
图12 构架有限元模型子结构划分
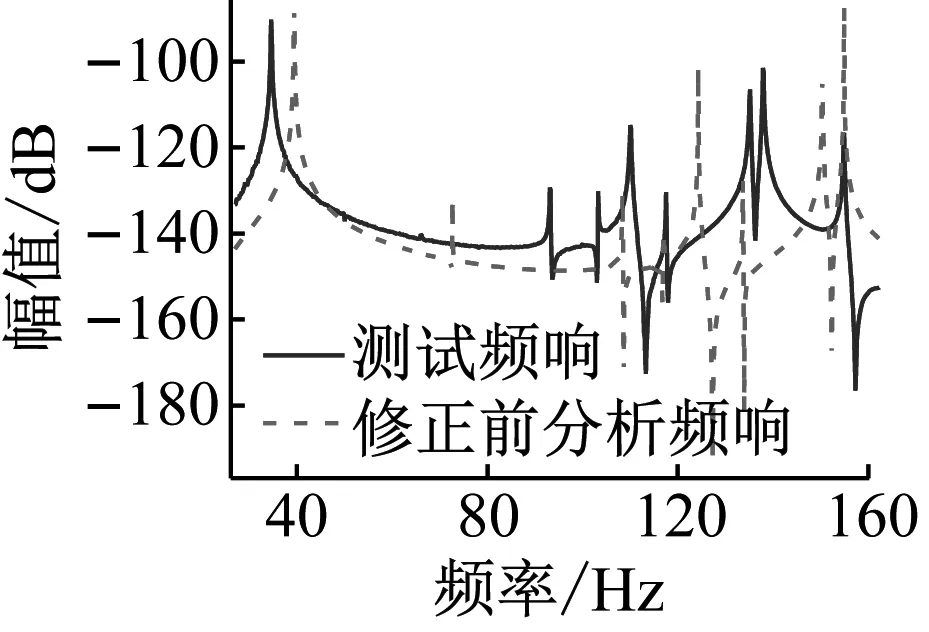
图13 修正前初始分析频响与测试频响对比
有限元模型划分为3个子结构进行模态综合。自然坐标下模型的自由度为181 356,模态综合坐标下模型自由度仅为1 830,大大减小了修正过程的矩阵运算规模。如图14、15所示,采用基于模态综合缩减基的方法进行修正,通过若干迭代步后,修正后分析频响与测试频响相关性有了很好的改善。
检验修正前后的模态频率变化,如表1所示,修正前后平均频率误差由12.72%降低至0.61%。因此,基于模态综合缩减基的方法不仅在初始分析频响与测试频响相关性较差、待修正参数较多、具有较大测试噪声干扰等情况下收敛性较好,且有效提高了模型修正的效率。若采用基于模态振型缩减基的方法,取80阶有限元模态作为坐标变换基矩阵,模态坐标下模型自由度为80,修正精度与基于模态综合缩减基的方法类似。
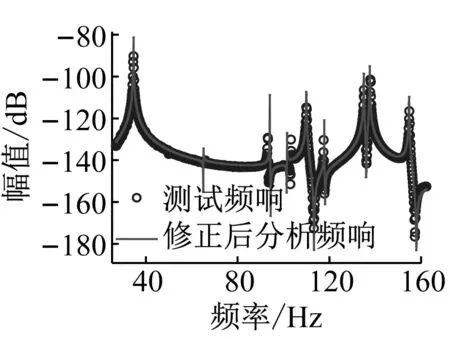
图14 修正后分析频响与测试频响对比

图15 修正前后分析频响与测试频响幅值相关性对比

表1 修正后各阶频率对比
3 结 论
针对规模巨大的有限元模型,本文提出了基于缩减基的频域有限元模型修正方法,通过数值算例与试验结构的模型修正表明:
(1) 对于自由度高达几十万的有限元模型,利用模态综合缩减基或模态振型缩减基可以有效减小矩阵运算规模,提高修正算法的计算效率。
(2) 在测试噪声较大、初始分析频响与测试频响残差较大、待修正参数较多等复杂情形下,本文方法仍具有较好的收敛性。
(3) 转向架模型修正中,本文方法修正后的分析频响与测试频响的相关性有较大的提高,这对实际结构在较复杂情形下的大型有限元模型修正具有一定的意义。
