强、弱连接对双塔连体超高层建筑风振响应的影响研究

吴华晓, 王钦华, 雷 伟, 祝志文,3, 李宏博

(1.汕头大学 土木与环境工程系，广东 汕头 515063； 2.西南科技大学 土木工程与建筑学院，四川 绵阳 621010; 3.广东省高等学校结构与风洞重点实验室，广东 汕头 515063)

连体超高层建筑是近十几年发展起来的一种新型建筑形式，由于其独特的建筑外形带来的强烈视觉效果使建筑更具有特色，该建筑形式深受业主和建筑师的青睐。已经建成的著名连体超高层建筑有苏州东方之门，马来西亚吉隆坡的双子塔等。该类建筑一般通过空中连廊连接两栋主体超高层建筑，空中连廊不仅可以作为连接两个主体建筑顶端的水平走廊，而且发生火灾等灾害时可以作为应急通道。空中连廊的连接形式可以分为强连接和弱连接。连廊两端刚接、两端铰接的连体结构属于强连接结构；连廊的一端与结构铰接，一端做成滑动支座，或两端做成滑动支座的连接为弱连接。双塔超高层建筑由于强连接作用，其动力特性与独立双塔结构完全不同[1-3]，包世华等对连体超高层建立了一个分段连续的串并联振动模型，导出了其弯扭耦连振动微分方程组，讨论了连廊不同刚度对结构动力特性的影响。Song等根据结构的层间侧移刚度建立了连体超高层建筑的分析模型，分析表明：连廊对结构动力特性影响非常大。

双塔连体超高层建筑的动力响应是该类结构设计关心的主要问题之一。目前，大部分研究主要集中在地震作用下双塔连体超高层建筑结构的动力分析[4-9]，抗震分析数学模型的建立、分析结果以及结论对该类结构抗风分析有一定的参考价值。在此，对双塔连体超高层建筑抗震分析做简单的介绍。Xu等[10]建立了流体阻尼器连接的连体建筑在地震作用下的运动方程，并分析了一多层连体建筑的实例，研究结果表明：如果阻尼器的参数选取合理，阻尼器能够减小该两栋建筑的地震响应。黄坤耀等将结构和连廊分别模拟为凝聚模型和有限刚度的弹性梁，在此基础上分析了连廊刚度对双塔连体高层建筑地震响应的影响，其分析结果为：对非对称双塔连体结构，当连体相对刚度小于0.002时，可以把双塔连体结构简化为独立双塔结构计算；当其大于0.90时，可以把塔楼连接楼层连同连体当作刚性楼层。肖从真等建立了北京丽泽SOHO超高层双塔连体结构的有限单元模型，分别分析了该建筑在九个连接方案下多遇地震响应，分析表明：在x方向，主要是单塔自行承受水平地震作用，九种方案的最大层间位移角基本一致，最小值仅比单塔无连桥的模型小6%。

与地震作用相比，风荷载有以下三个方面的特点：①风荷载与建筑物的体型有关[11]，可以分解成由来流湍流引起的顺风向风荷载和漩涡脱落引起的横风向风荷载；②风荷载功率谱的卓越频率与地震动的不同[12]；③当干扰建筑存在时，会产生较强的干扰效应[13]。在连体双塔超高层建筑的抗风分析方面，陈凯等[14]采用塔楼-连廊的整体结构模型对连体结构空中连廊的风振响应进行分析，结果表明：连廊的运动主要是由于塔楼主体运动引起的，连廊自身风压对其风致响应的贡献极小；两座塔楼的相对运动与横梁的轴力有很强的相关性，是造成横梁受拉压的主要因素。Song等[15]基于刚性楼板假设提出了连体双塔超高层建筑三维风振响应模型，由同步多点测压风洞试验获得矩形截面连体双塔超高层建筑的风荷载，在此基础上开展了风振响应分析，分析表明：由于连廊增加了其刚度，连体超高层建筑的风振响应要小于独立的双塔结构。王钦华等[16]将多个调谐质量惯容阻尼器(MTMDI)连接到连廊上，用来控制连体超高层建筑的风振响应。研究结果表明：虽然两个TMDI的总质量和总惯容量值比单个TMDI相应的参数小，但两者的减振效果基本相同，两者都能有效地减小两栋建筑在各个风向角下的加速度响应；对于位移响应，两者都可以减小高栋建筑的响应，低栋建筑在少部分风向角下其减振效果并不理想。

本文在以上研究的基础上对强、弱连接对超高层建筑风振响应的影响进行研究，主要研究内容包含：①在刚性楼板假设的基础上，基于结构的层间侧移刚度建立了平行放置连体双塔结构在风荷载下的运动微分方程；②基于某连体双塔超高层建筑(建筑A为268.0 m、建筑B为210.2 m)实例的同步多点测压风洞试验，进行风振响应分析，讨论了强、弱连接对结构风振响应的影响。研究结果对连体超高层建筑抗风设计提供参考。

1 强和弱连接双塔连体超高层风振响应分析模型

并列放置连体双塔超高层建筑弱、强连接的示意图分别如图1(a)和(b)所示。该连体超高层由建筑A(共i层)和建筑B(共j层)组成，且两栋建筑由连廊相连，连廊连接建筑A的第s层与建筑B的第r层。为了建立其在风荷载下的运动方程，引入以下假设：

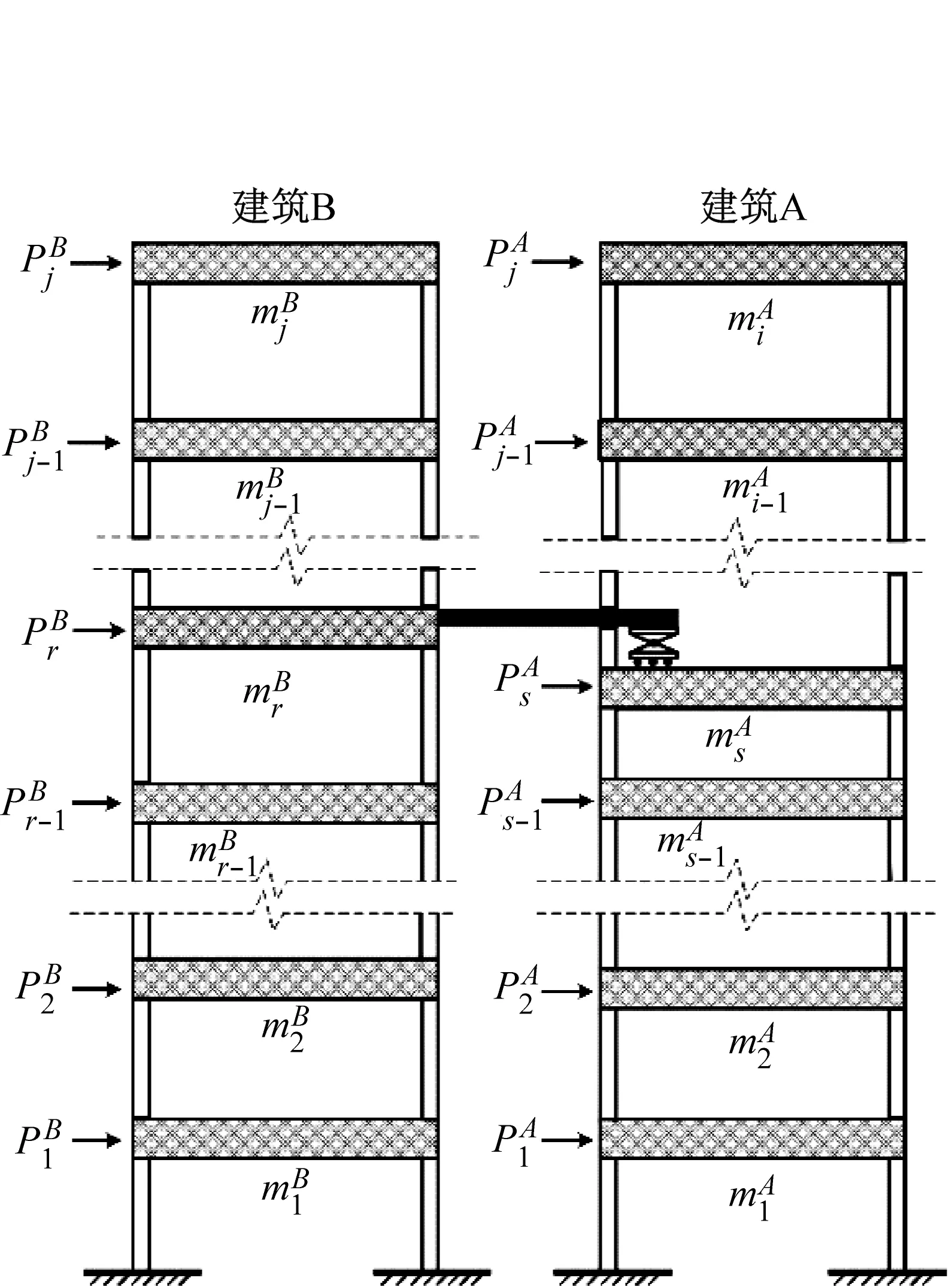
(a) 弱连接

(1) 建筑楼板平面内刚度为无限刚性，楼板平面外刚度忽略不计；

(2) 将弱连接简化为一端为固定、一端为滑动支座的连接；

(3) 强连接两端均为刚性连接，只考虑连廊轴向力的作用，可以将连廊简化为图1(b)所示的弹簧和阻尼体系；

(4) 连廊沿结构刚度较弱的方向布置，因此可以仅考虑连接方向上的振动，不考虑另外一个方向以及扭转振动。

在以上假设的条件下，双塔连体超高层建筑在风荷载作用下的运动方程可以表示为

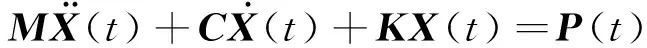
(1)

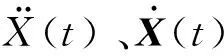
(2)

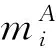
当连廊的连接形式为强连接形式时(图1(b))，即连廊两端分别与建筑A、B刚接，考虑连廊的阻尼和刚度对结构的影响，则结构的阻尼矩阵可以写为

(3)

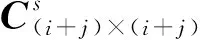
(4)

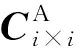
(5)

k=1,2,…,i

(6)

式中:ΦA、ξA,k和ωA,k分别为建筑A的模态矩阵、第k阶阻尼比以及自振频率。φA,k和MA,i×i分别为建筑A的第k阶模态向量和集中质量矩阵。同理根据式(5)和(6)可以计算建筑B的阻尼矩阵，相应的计算参数均取建筑B的即可。对于结构的刚度矩阵可以表示为

(7)

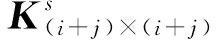
(8)

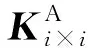
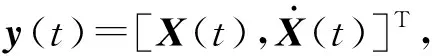
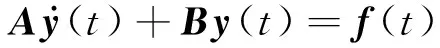
(9)

其中，A、B矩阵以及向量f(t)可以表示如下

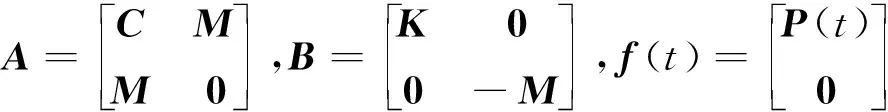
(10)

采用复模态叠加方法计算状态空间响应y(t)，如下式所示

(11)

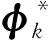
(12)

式中:Φ为连体结构体系的模态矩阵;ΦT连体结构体系的模态矩阵的转置。

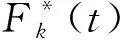
(13)

结构的风致峰值响应可以由式(11)表示的响应时程统计获得。

2 实例分析

本文以一栋双塔连体超高层建筑为实例进行分析，其中建筑A为59层(共268 m)，建筑B为55层(共210.2 m)，建筑A的第45层与建筑B的第54层通过连廊连接，详细平面尺寸如图2所示。由于其沿x方向侧移刚度较小，因此本文仅考虑在该弱轴方向上强连接与弱连接对结构风振响应的影响。

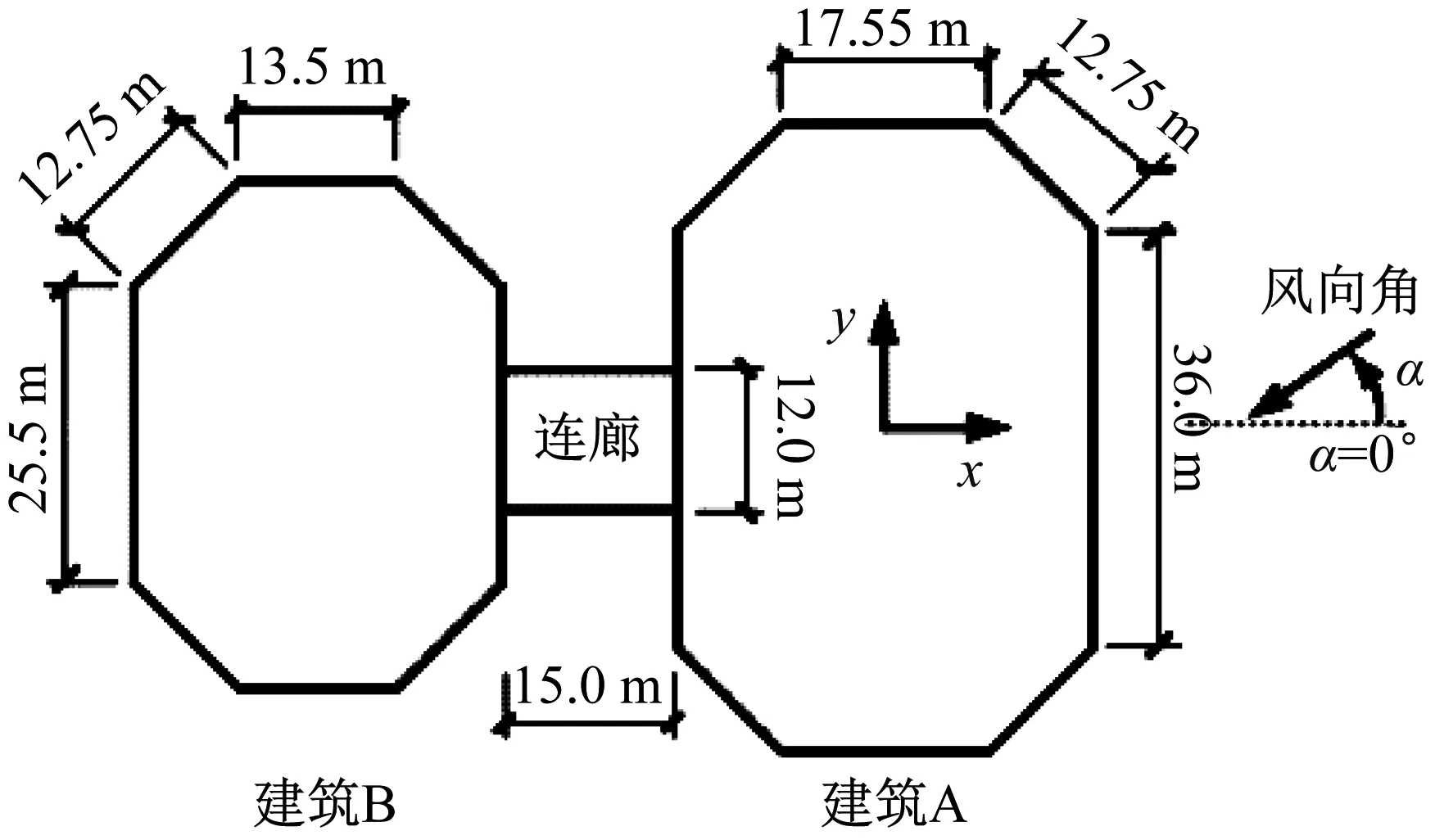
图2 平面尺寸及坐标系的定义

该双塔连体超高层建筑刚性模型同步测压风洞试验在汕头大学风洞实验室进行，模型的试验缩尺比为1∶300，模拟的地貌类型为B类，其中风速和湍流强度剖面如图3所示。试验每间隔15°风向角共进行24个风向角的风洞试验，风向角的定义如图2所示，其详细试验信息可参考相关文献[16]。根据GB 50009—2012《建筑结构荷载规范》，计算位移和加速度响应时的基本风压分别取为0.6 kPa(50年重现期)和0.35 kPa(10年重现期)。

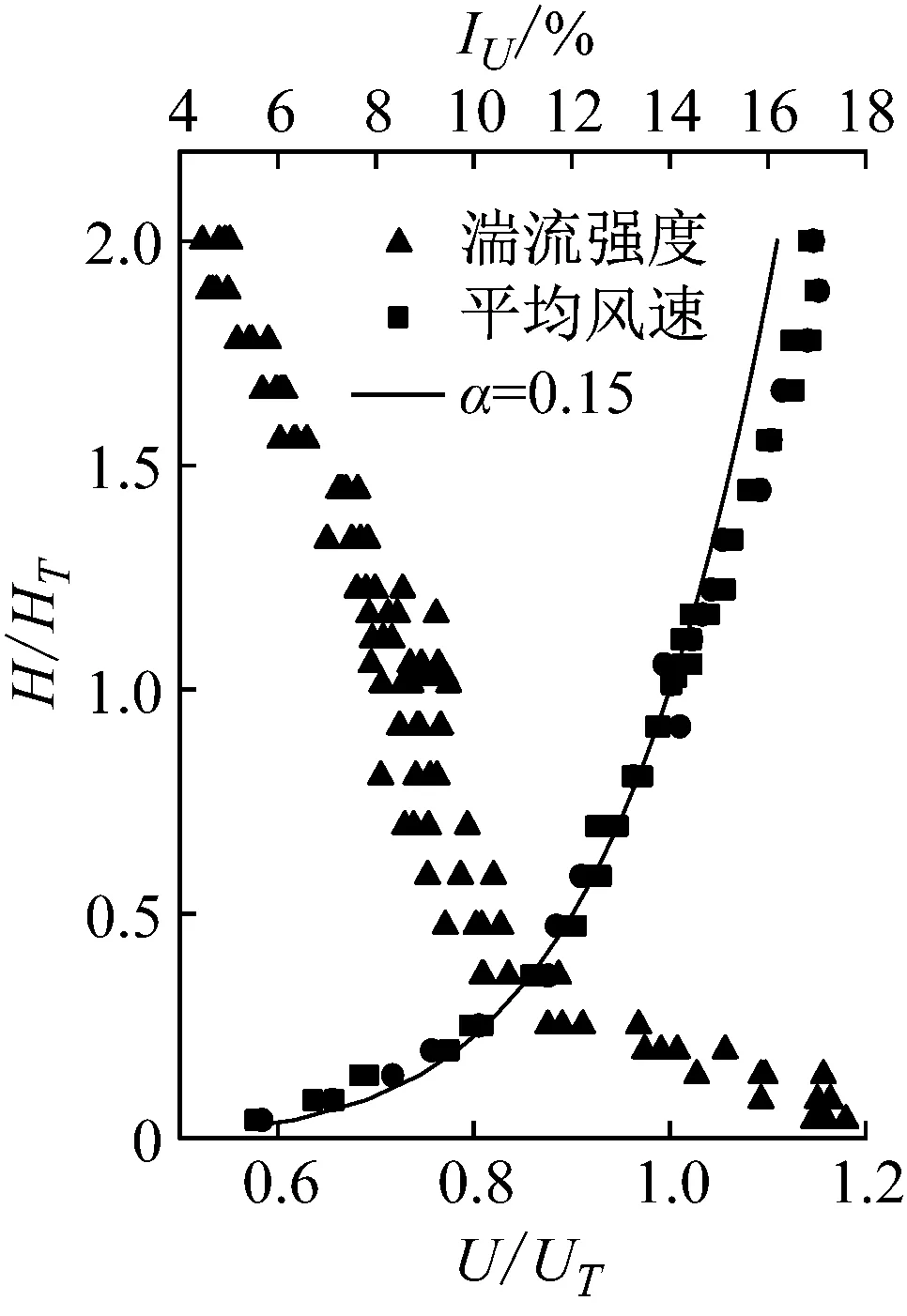
图3 风剖面及湍流度剖面

2.1 风荷载以及结构的动力特性

由缩尺理论可获得作用在该建筑各楼层上的风荷载时程，图4(a)和(b)分别为在90°风向角下建筑A第54层和建筑B第50层的x方向上的气动力时程及其归一化力谱。从图4可以看出，建筑A、B在横风向下的力均值都接近0。另外，在建筑A第54层的归一化力谱上有一个明显的峰值，即横风向漩涡脱落频率，但是在建筑B第50层的归一化谱上没有出现明显的高于其他频率点的峰。原因在于建筑A的第54层的高度比建筑B顶层的高度高，其风荷载不受建筑B的干扰，相反建筑B的第50层的高度比建筑A顶层高度低，其风荷载被建筑A干扰。

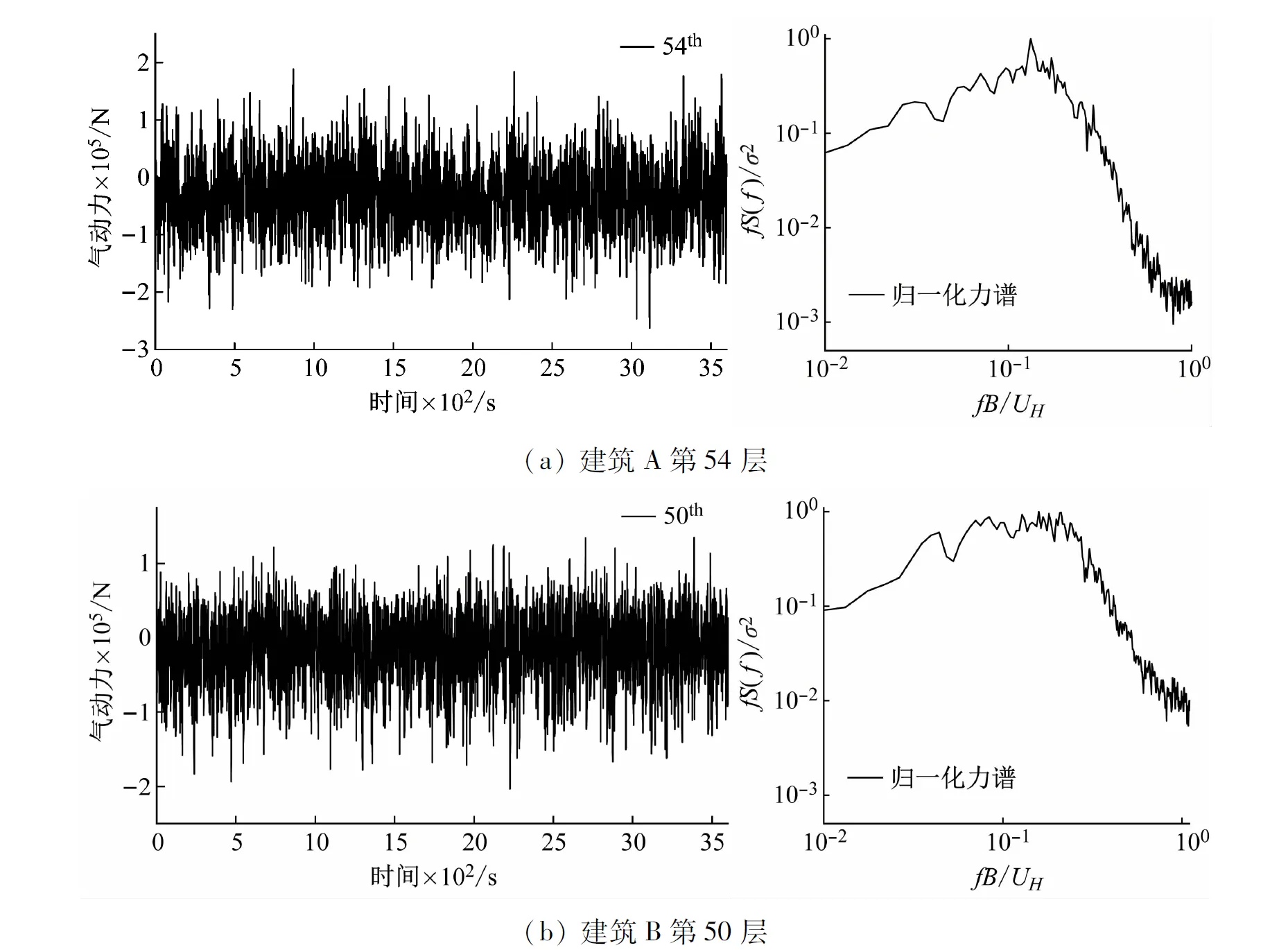
图4 气动力时程及其归一化力谱

表1比较了强与弱连接形式下双塔连体超高层建筑的前四阶的自振频率，在弱连接形式下，结构的第一、二阶频率分别为0.139 Hz、0.161 Hz，分别表现为建筑A、B的第一阶的自振频率。而在强连接形式下，结构的第一、二阶频率都增大，表明在连廊的影响下，结构的刚度得到增强。图5列出了强弱连接时候，连体结构的前两阶模态。从图中可以看到：弱连接形式下，第一、二阶模态分别对应建筑A和建筑B的模态，因此弱连接形式对两栋建筑振型不会产生影响；在强连接形式下，结构的振型与弱连接有明显的不同。

表1 强与弱连接形式下前四阶的自振频率比较

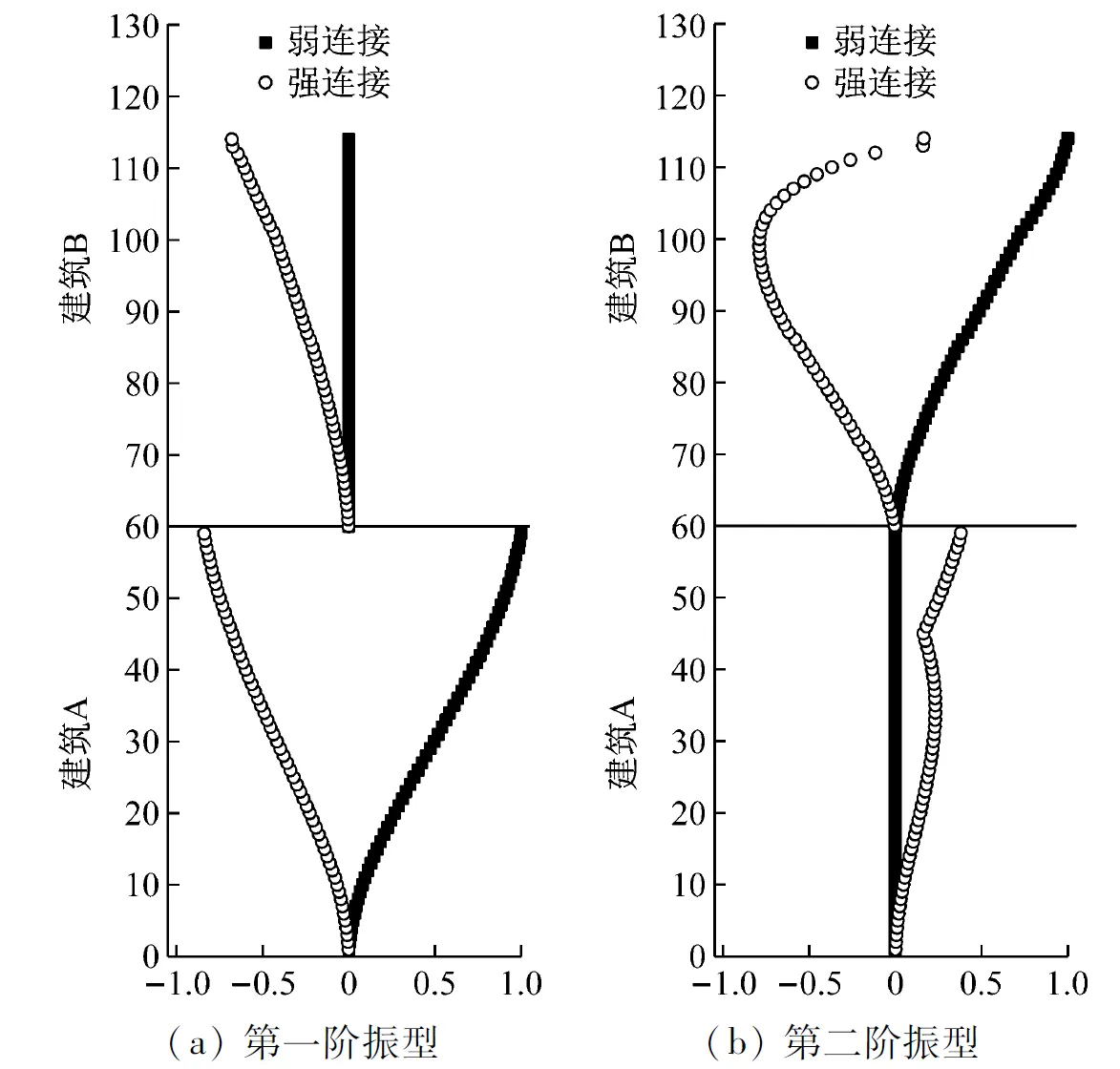
图5 归一化模态位移比较

2.2 连接形式对风振加速度响应的影响

在计算结构加速度和位移响应时，前三阶阻尼比分别取为1.5%和3%，其他阶阻尼比可由相关规范以及文献取得[17]。由式(11)获得风致加速度时程响应后，可以统计获得建筑风致加速度响应峰值，图6(a)和(b)分别表示建筑A和建筑B的顶层的峰值加速度响应随风向角的变化。在弱连接的条件下，建筑A和B均在90°和270°风向角下(横风向)的峰值加速度较大，但建筑B在0°风向角下峰值加速度也较大，原因是在该风向角下建筑B完全位于建筑A的尾流区。建筑A和建筑B在大部分风向角下，强连接形式时的峰值加速度都小于弱连接形式时的峰值加速度，在强连接形式下由于连廊的作用，建筑B的峰值加速度减小程度要比建筑A的大。

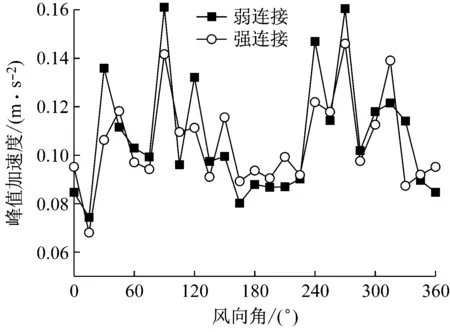
(a) 建筑A

为了量化连接形式对风振响应的减小作用，定义减振因子β如下

(14)

式中:Rw和Rs分别为弱、强连接形式下的峰值加速度或位移响应。表2列出了两种连接形式下0°、90°和270°风向角峰值加速度及减振因子。

从表2中可以看出，在0°风向角下，建筑B的峰值加速度从弱连接形式下的0.18 m/s2减小到强连接形式下的0.06 m/s2，减小了66.9%，但是对建筑A的横风向角的控制效果都较差。从已有文献[16]来看，将调谐质量惯容阻尼器(tuned mass damper inerter,TMDI)连接在连廊上对两栋建筑的峰值加速度控制效果要优于强连接作用下的控制效果。

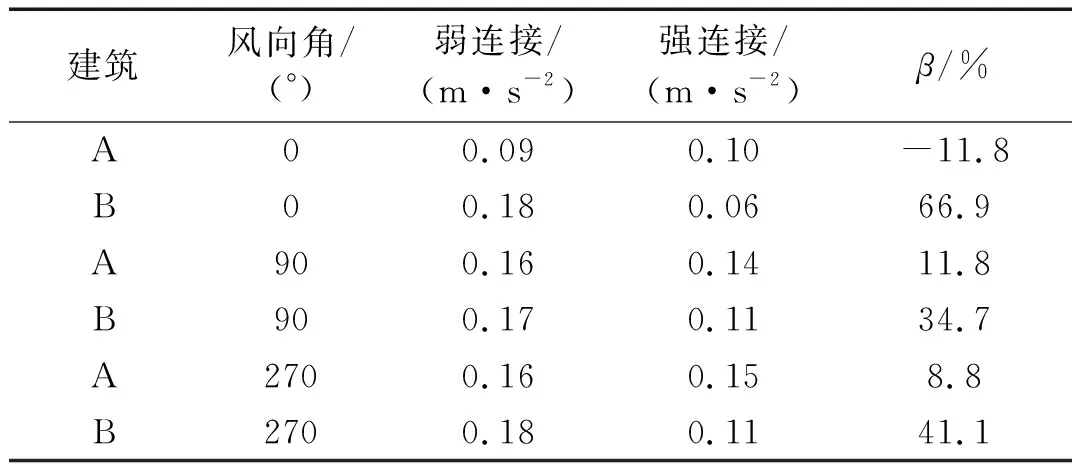
表2 典型风向角下强与弱连接形式下峰值加速度减振因子

图7为建筑A和建筑B的顶层加速度响应在90°风向角下沿楼层的比较，从图中可以看出，在强连接形式下建筑A和建筑B的峰值加速度响应沿整个楼层的值都是小于弱连接形式下对应的值。

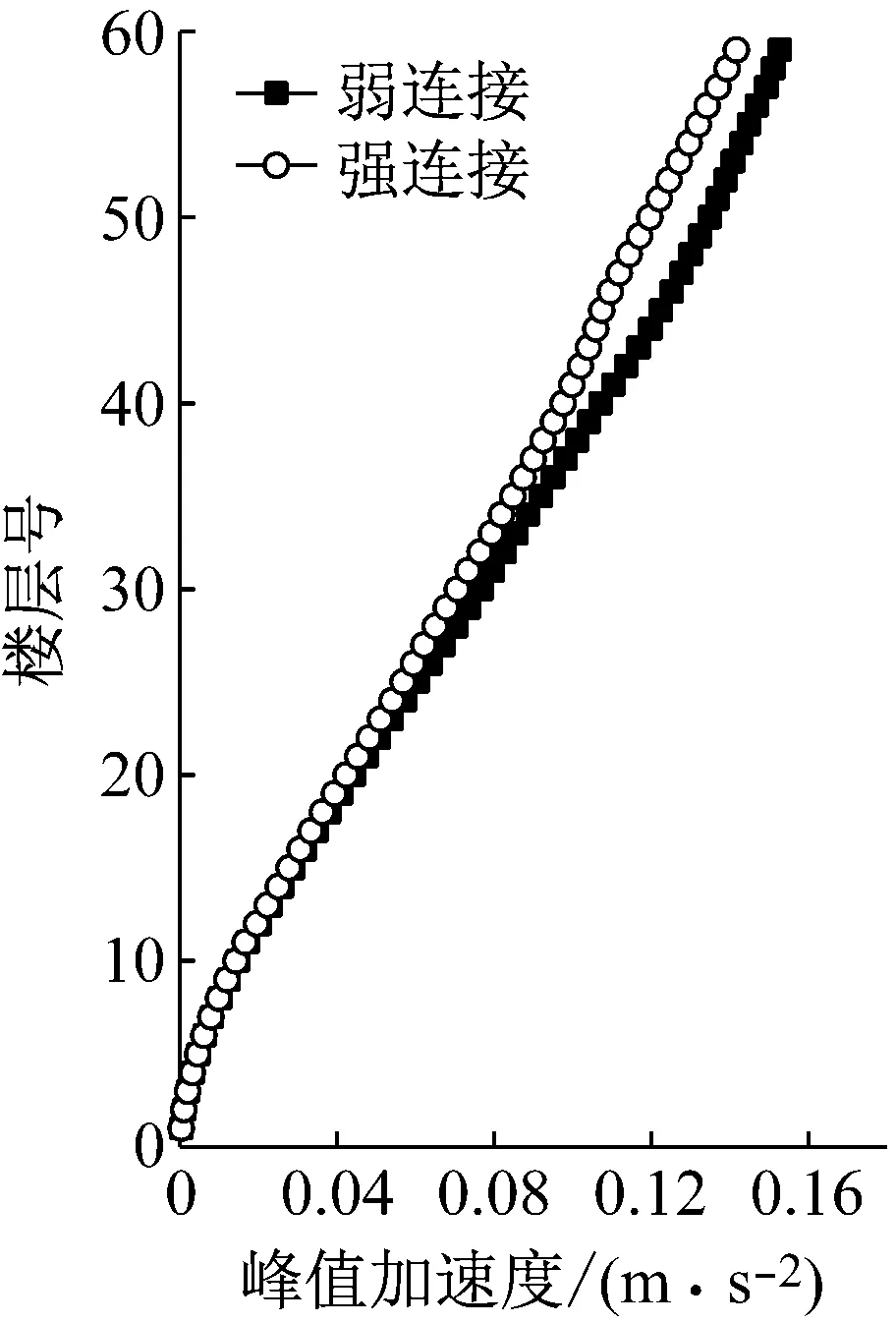
(a) 建筑A

2.3 连接形式对风振位移响应的影响

由式(11)获得风致位移时程响应后，统计获得风致位移响应峰值，图8(a)和(b)分别表示建筑A和建筑B的顶层峰值位移响应随风向角的变化。其中，在强连接形式下建筑A和建筑B在105°～270°风向角区间下峰值位移响应均为正值，而在其余风向角下位移响应均为负值，两栋建筑顶层的峰值位移方向相同。对于建筑A，强连接形式能减小大部分风向角下的峰值位移。但是对于建筑B，由于连廊的强连接作用，在部分风向角下，其峰值位移的方向发生了改变，导致其峰值位移方向与建筑A相同，原因是在强连接形式下建筑A的运动主导了整个结构的运动。为了解释这个原因，图9对连廊位置处两个楼层的峰值位移沿风向角的变化进行了分析。

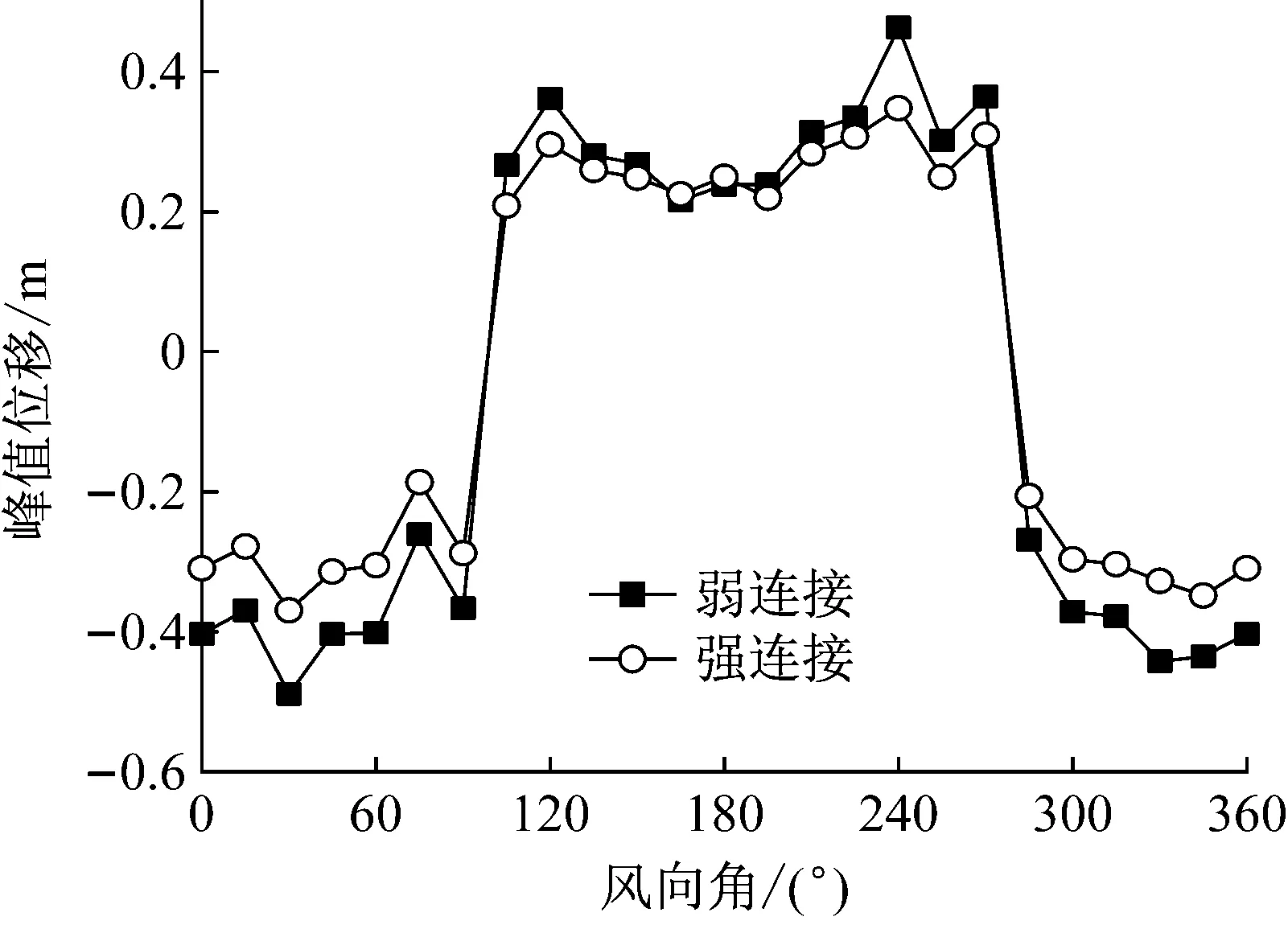
(a) 建筑A

图9表明弱连接形式下，两栋建筑在0°～30°、255°～270°和345°风向角下位移方向相反，在强连接形式下，两栋建筑在连廊位置处楼层沿各个风向角的峰值位移几乎相同，且与弱连接形式下建筑A的位移方向一致，表明在强连接形式下建筑A的运动主导了整个结构的运动，导致建筑B的位移运动方向与建筑A相同。

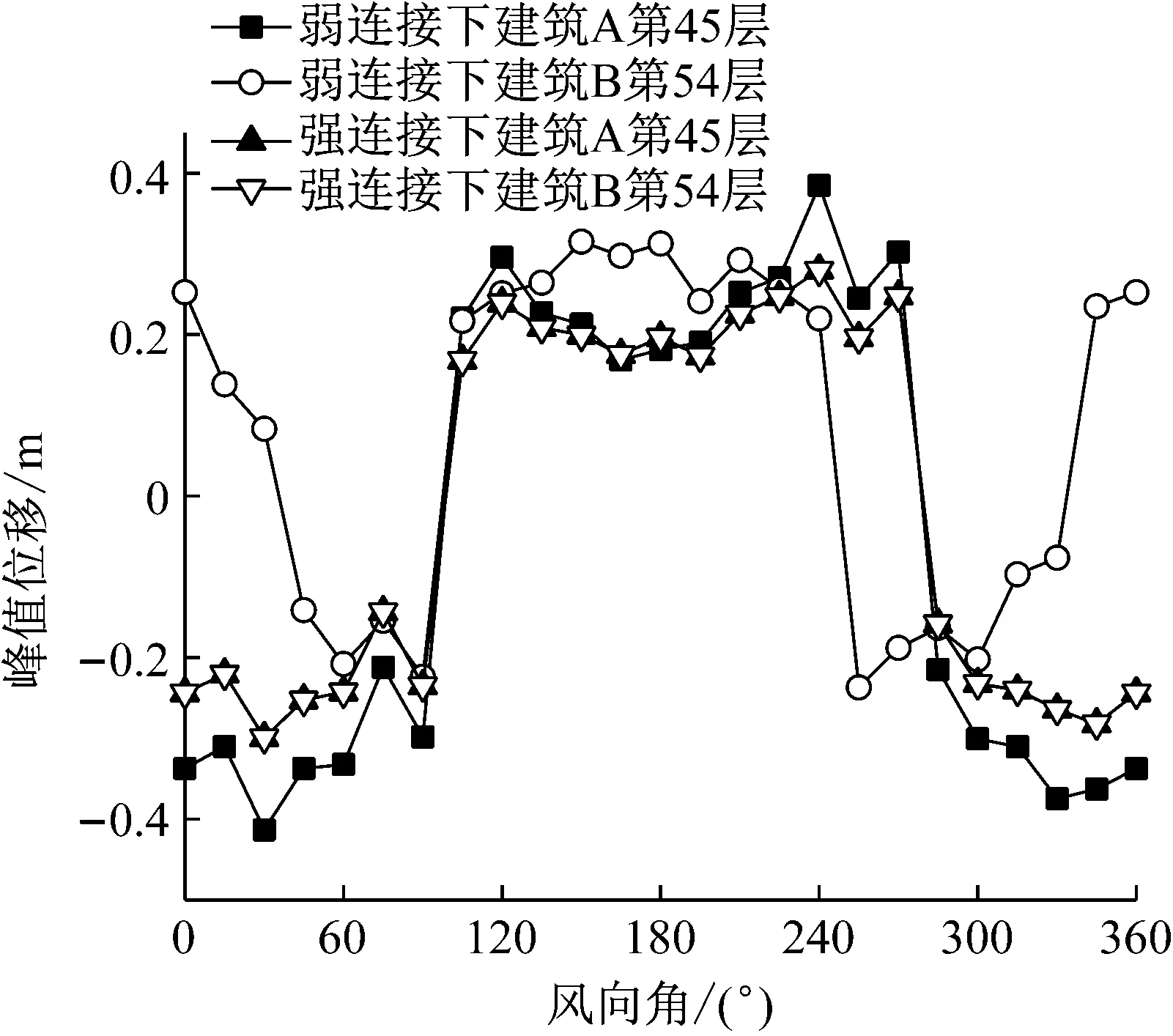
图9 连廊位置楼层处的峰值位移沿风向角的变化

表3列出了两种连接形式下的典型风向角峰值位移及减振因子。可以看出，在0°风向角下，建筑B的峰值位移从弱连接形式下的0.26 m变化为强连接形式下的-0.25 m，变化了196%，在270°风向角下也有类似的情况出现。原因是由于连廊的强连接，建筑A主导了整个结构系统的运动，导致两栋建筑的位移有相同的运动趋势且位移方向相反。

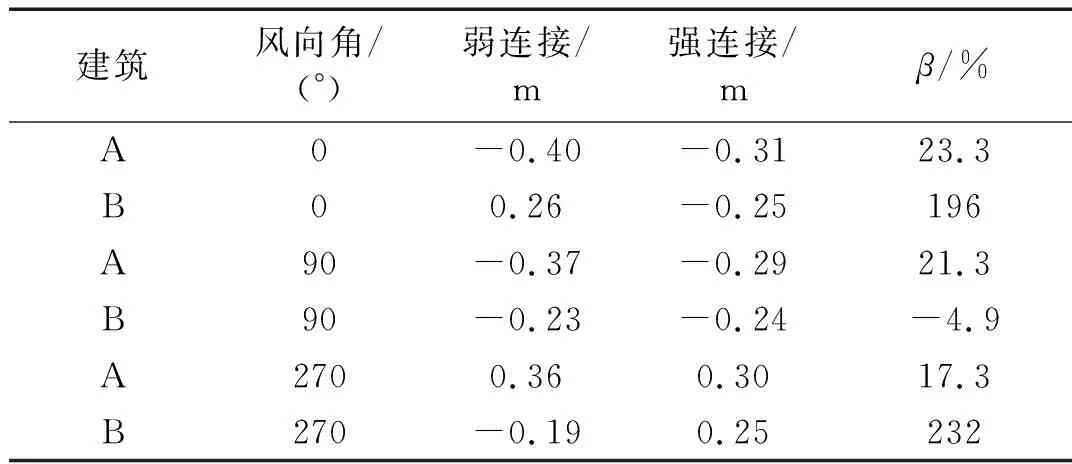
表3 典型风向角下强与弱连接形式下峰值位移减振因子

图10为建筑A和建筑B的顶层峰值位移响应在90°风向角下沿楼层的比较，从图中可以看出，在强连接形式下，建筑A的峰值位移响应沿整个楼层的值都是小于弱连接形式下的值，但是在建筑B楼层强弱连接形式下的峰值位移变化不大。

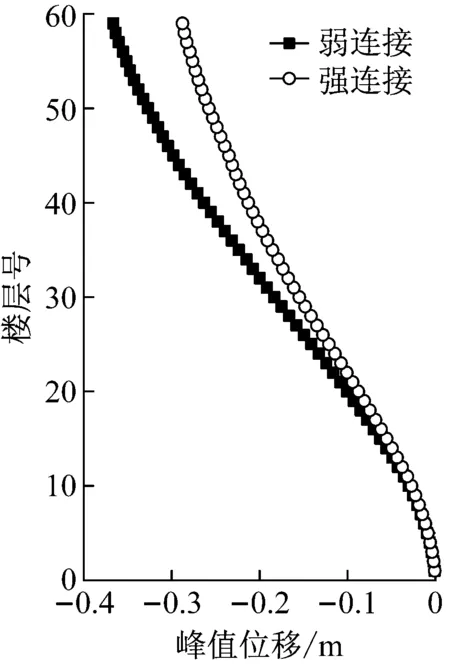
(a) 建筑A

3 结 论

本文建立了强、弱连接双塔连体超高层建筑风振响应分析的数学模型，通过风洞试验得到作用在各楼层的荷载时程向量，最后，计算了强、弱连接对两栋建筑峰值加速度和位移的影响，得到以下结论：

(1) 从两栋建筑弱、强连接两种形式下结构动力特性分析表明：强连接使结构的第一、二阶频率都增大，在其影响下，结构的刚度得到增强。

(2) 强连接形式下的两栋建筑的顶层峰值加速度在22个风向角下都小于弱连接形式下的峰值加速度，其中，建筑A的减小幅度小于建筑B，在90°风向角时，建筑A顶层峰值加速度从弱连接形式下的0.16 m/s2减小到强连接形式下的0.14 m/s2，减小了11.8%；，建筑B顶层峰值加速度从弱连接形式下的0.17 m/s2减小到强连接形式下的0.11 m/s2，减小了34.7%。

(3) 强连接形式下建筑A的顶层峰值位移较弱连接形式有所减小。例如，在270°风向角下，建筑A顶层的峰值位移由弱连接形式下的0.36 m减小到强连接形式下的0.30 m，减小了17.3%。强连接形式下建筑A会主导整个结构的运动，导致建筑B与建筑A有相同的运动方向。例如，在270°风向角下，建筑B顶层的峰值位移则由弱连接形式下的-0.19 m变化到强连接形式下的0.25 m，其位移方向发生了改变。