强噪声作用下复合材料壁板气动弹性摩擦非线性振动
2021-07-14张君贤瞿叶高谢方涛郭其威张崇峰
张君贤, 瞿叶高, 谢方涛, 郭其威 , 张崇峰
(1.上海交通大学 机械系统与振动国家重点实验室,上海 200240;2.上海宇航系统工程研究所,上海 201108;3.上海航天技术研究院,上海 201109)
为了减轻结构重量并提高结构强度,在高速飞行器结构设计中广泛采用复合材料层合壁板。在高速飞行时,壁板常常处于气动载荷和噪声载荷联合作用下的复杂力学环境中。由于制造和装配过程中产生的误差,非光滑摩擦界面广泛存在于结构边界处(例如飞行器壁板连接处),导致壁板产生复杂的非线性动力学行为。Dowell[1]基于von Karman非线性应变和完全线性化气动载荷模型研究了壁板的颤振行为,分析了不同马赫数和板的长宽比对壁板产的影响。Shore等[2-4]基于有限元方法建立了壁板的非线性颤振数值模型,研究了不同边界条件以及不同来流角度的气动载荷对壁板颤振特性的影响。Dhainaut等[5]研究了热和声载荷联合作用下复合材料壁板的随机振动响应,分析了壁板的线性随机振动、跳变运动和非线性随机振动等响应。Vahid等[6]采用三次NURBS基函数建立了板的几何形状,分析了斜层合板的自由振动和线性颤振问题,结果表明,斜板两端的纤维方向对其颤振稳定性有显著影响。Pacheco等[7]研究了柔性梁加固板的颤振问题,结果表明将加强筋建模为不动边界会高估颤振边界。Guimarães等[8]分析了复合材料壁板的纤维轨迹对复合材料板气动弹性的影响,指出对纤维的牵引转向是提高复合材料板气动弹性和屈曲性能的有效手段。在国内,夏巍等[9-10]针对飞行器壁板的气热弹性问题开展了一系列研究,提出“穿零频次”的概念对热声载荷联合作用下壁板的跳变运动特性进行了研究[10]。沙云东等[11]从结构势能出发,认为跳变运动是因为屈曲后平板的势能曲线出现了两个势能井,较大的激励使平板在两个势能井间跳跃,而当温度增加时势能井加深,跳变运动逐渐被限制在单一势能井中。Chai等[12]研究了基于弹性地基的点阵夹芯板在超音速气流作用下的热弹性颤振和热屈曲特性,并利用弹性地基实现在不影响结构固有频率的情况下消除结构的热屈曲。Sun等[13]导出了二维壁板在经典齐次边界条件下颤振问题的解析结果,并基于精确解进行了气动力作用下壁板的动力学响应分析。Lin等[14]研究了含形状记忆合金的复合材料壁板在热、气动载荷和声载荷共同作用下的动力学响应,结果表明形状记忆合金可以显著改变复合材料的振动特性。Jiang等[15]研究了梯形复合材料层合板在超音速气流作用下的热弹性问题,详细分析了铺设参数和气流方向等对壁板热屈曲和颤振边界的影响。针对含摩擦边界的振动结构,国内外学者也开展了相关研究。Lassalle等[16]采用谐波平衡法和实验研究了摩擦阻尼作用下叶片圆盘的非线性气动弹性行为。Xie等[17]采用宏观黏滑摩擦模型模拟了摩擦边界,基于有限元方法建立了含摩擦边界的复合材料层合壁板颤振的数值模型,研究了摩擦边界参数对层合壁板颤振响应的影响。
本文基于von Karman型非线性应变、Reddy三阶剪切锯齿理论和准稳态一阶活塞理论,采用高斯限带白噪声模型计算壁板所受声压,利用宏观黏滑摩擦模型对摩擦边界进行建模,建立了强噪声载荷作用下含摩擦边界复合材料壁板的气动弹性非线性动力学有限元数值计算模型。研究了在不同声压和气动载荷联合作用下壁板的非线性振动响应,在此基础上分析了摩擦边界正压力对壁板振动响应的影响。
1 动力学方程
含摩擦边界的复合材料壁板模型如图1所示,其中a,b和h分别表示壁板的长度、宽度和厚度。在壁板中面上引入笛卡尔坐标系o-xyz,其中高速气流沿着x轴正方向流过,有限带宽的高斯随机噪声载荷以声压Pacoustic的形式沿着z轴负方向均匀作用于壁板表面。不失一般性,假设摩擦边界沿着x=x1至x=x2分布在y=b边界上。

图1 含摩擦边界的复合材料壁板
采用Reddy三阶剪切锯齿理论来描述复合材料壁板的振动变形。层合板内任意一点处的位移可以表示为
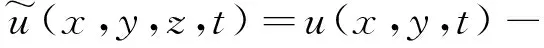
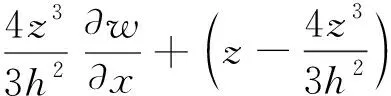
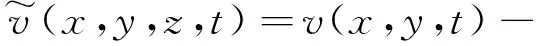
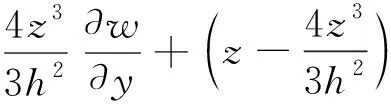
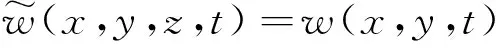
(1)
式中:u,v和w分别表示层合板中面上任意一点沿x,y和z方向的位移分量;ϑ1,ϑ2,η1和η2为中面上的广义位移变量。φ(z,k)为锯齿函数,用于满足层合板厚度方向位移场分段连续性条件,其表达式为
(2)
式中:zk和zk+1表示第k铺层下表面和上表面的z坐标;hk=zk+1-zk代表第k铺层的厚度。
考虑壁板的几何非线性大变形效应,采用von Karman位移-应变关系得到层合板内任意一点处的应变为
(3)
第k层壁板铺层的应力分量可表示为
(4)

应用准稳态一阶活塞理论,得到作用在复合材料壁板上的气动力为
(5)
式中:λ和RM分别代表无量纲动压和无量纲气动阻尼;D110为当层合板中所有纤维方向都与气流方向相同时壁板弯曲刚度矩阵中的第一个元素,具体表达式见文献[5]。
采用有限带宽高斯白噪声来描述均匀施加在壁板表面上的随机气动噪声载荷。当指定声压级SPL时,采用下式计算声载荷的功率谱密度[18]
(6)
式中:p0代表参考声压,p0=20 μPa;fc为声载荷的上截止频率。
根据功率谱密度可以得到有限带宽高斯白噪声的声压表达式
(7)
式中,n代表时域范围内需要计算的所有时间步。
采用如图2所示的宏观黏滑摩擦模型计算摩擦边界上的摩擦力。图中m为摩擦边界中包含的有限元节点个数。当由壁板变形产生的弹性力小于临界摩擦力时,摩擦边界处于黏滞状态并且等效为刚度为kt的线性弹簧支承边界;当弹性力大于临界摩擦力时,摩擦边界转换为滑移状态,此时接触面间发生滑动并且产生一个大小恒定的摩擦力作用在摩擦边界上。基于宏观黏滑摩擦模型计算的摩擦力为
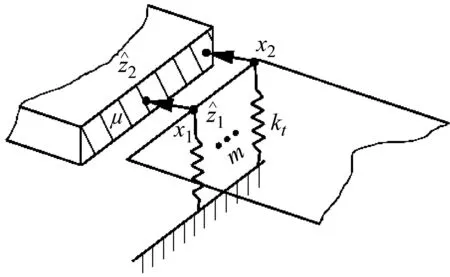
图2 宏观黏滑摩擦模型
(8)
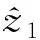
(9)

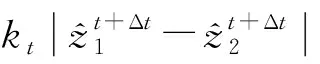
强噪声和气动载荷联合作用下含摩擦边界复合材料壁板的非线性气动弹性动力学方程由Hamilton原理推导得出

(10)
式中:T和V分别代表层合板的动能和应变能;Wareo,Wf和Wacoustic分别表示由气动载荷,边界摩擦力和随机声载荷所做的功。T,V,Wareo和Wf的表达式见文献[17]。声载荷所做的功δWacoustic可以表示为
(11)
式中,Pacoustic为根据式(6)计算得到的声压载荷。
将δT,δV,δWareo,δWf和δWacoustic的表达式代入式(9)并采用有限元方法对壁板进行离散,可以得到壁板的非线性动力学方程
(12)

2 算例及讨论
本节选取的研究对象为正方形壁板,其几何尺寸为:0.3 m×0.3 m×0.000 9 m;所有铺层的厚度相等,铺设方式为[0°/90°/0°/0°/90°/0°]s,每个铺层的材料参数为:E1=69 GPa,E2=10 GPa,μ12=0.22,G12=G13=G23=4.55 GPa,ρ=1 550 kg/m3。 层合板的边界条件为:x=0 m和x=0.3 m两条边上为简支边界条件,在y=0.3 m的边上沿x=0.15 m至x=0.3 m为摩擦接触面,其余边界自由。摩擦边界的接触刚度kt=1×105N/m,正压力N0=50 N,摩擦因数μ=0.3。
2.1 结果验证
为了验证计算程序的正确性,计算了四边简支壁板的前两阶固有频率随无量纲动压λ的变化规律,并与文献[19]进行了对比,对比结果如图3所示,从图中可以看出本文结果与已有文献中的结果吻合得很好。
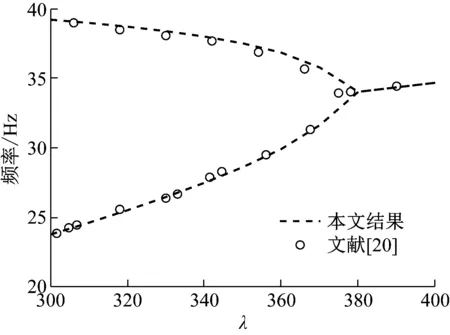
图3 四边简支壁板的固有频率随无量纲动压λ的变化曲线
2.2 强噪声作用下复合材料壁板的颤振特性分析
如前所述,当摩擦边界处于黏滞状态时,摩擦边界为线性弹簧支承边界。因此,在计算壁板的颤振临界动压时,将壁板的摩擦边界替换成一系列刚度大小为摩擦边界接触刚度的线性弹簧即可。如图4为摩擦壁板的前四阶固有频率随无量纲动压λ的变化曲线。结果表明,随着λ逐渐增加,第二阶和第三阶固有频率逐渐相互靠近并且在λ≥273时重合,因此可以得到壁板的临界颤振动压为λcr=273。

图4 壁板固有频率随无量纲动压λ的变化曲线
图5为作用在壁板表面上的气动噪声载荷的时域波形,声压级取为90 dB。图6为在声压级为90 dB的噪声载荷作用下,无量纲动压分别为λ=0,λ=210,λ=300和λ=330时层合板几何中心处的横向振动位移响应。结果表明,来流动压较小时,气动载荷幅值较小,壁板没有产生稳定的颤振响应,如图6(a)和图6(b);而随着来流动压的增大,壁板发生颤振响应,如λ=300时的响应曲线的幅值开始趋于稳定,当λ=330时壁板振动的幅值基本稳定。这表明,随着气动载荷的增大,气动载荷逐渐对壁板的颤振响应占据主导作用。图7给出了无量纲动压为λ=0和λ=330时,层合板的横向振动位移响应的概率密度。图中的曲线是按照每组数据的平均值与标准差作为参数作出的正态分布曲线。结果表明,仅有声压载荷作用时(即λ=0),层合板的横向振动位移响应的分布基本符合正态分布,其与作用于层合板表面上的声压载荷分布形式是一致的;而当λ=330时,层合板的横向振动位移响应分布呈现为一个双峰分布,这表明壁板的振动响应在两个峰值之间振荡,也即气动载荷主导下的极限环运动特征。
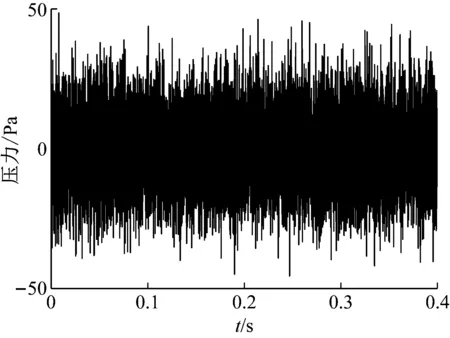
图5 随机声压载荷(90 dB)
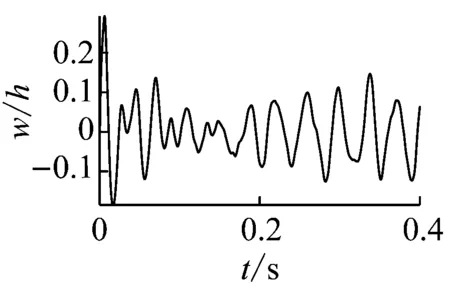
(a) λ=0

(a) λ=0
将气动载荷λ=330时的噪声载荷提高至120 dB,得到的壁板中心的横向振动位移响应与响应的概率密度,如图8所示。结果表明,层合板的横向振动位移响应相比于噪声载荷为90 dB的情况显著增大,但层合板的极限环颤振特征已经消失,层合板的振动表现为接近于正态分布的随机振动,这种情况下噪声载荷对于层合板的振动响应占据主导作用。
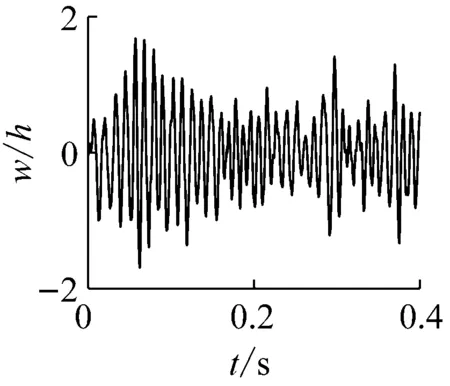
图8 声载荷(120 dB)和气动载荷(λ=330)联合作用下壁板位移响应及其概率密度
2.3 摩擦边界正压力对壁板响应的影响
首先考虑仅有气动载荷作用下的含摩擦壁板的非线性振动响应。图9给出了无量纲动压λ=330作用下,取摩擦边界上正压力为N0=0.05 N和N0=50 N时,计算得到的层合壁板几何中心处的横向振动响应。从图中可以看出,正压力取50 N时,层合板的横向振动位移响应幅值明显大于正压力为0.05 N的情况。通过计算,得到两种正压力条件下,层合板摩擦边界上宏观黏滑模型的临界摩擦力大小分别为15 N和0.015 N。图10(a)给出了位于壁板x=0.15 m,y=0.3 m处的摩擦力曲线。从图中可以看出所有时刻的摩擦力绝对值均小于临界摩擦力,此时摩擦边界处于完全黏滞状态并可以等效为弹性支承边界,且由于仅有气动载荷作用下壁板的振动类型为极限环振动,因此稳定后的摩擦力也呈现一定的周期性。图10(b)则给出了同样载荷情况下但正压力为0.05 N时,位于壁板同一位置处的摩擦力曲线。结果表明层合壁板的振动存在明显的黏滞与滑移运动状态相互切换的现象。根据上一节的理论分析可知,处在滑移状态的摩擦边界存在着相对滑动,从而耗散了壁板的振动能量,因此这种情况下的层合壁板振动响应相比于正压力50 N作用下完全黏滞的壁板响应更小。
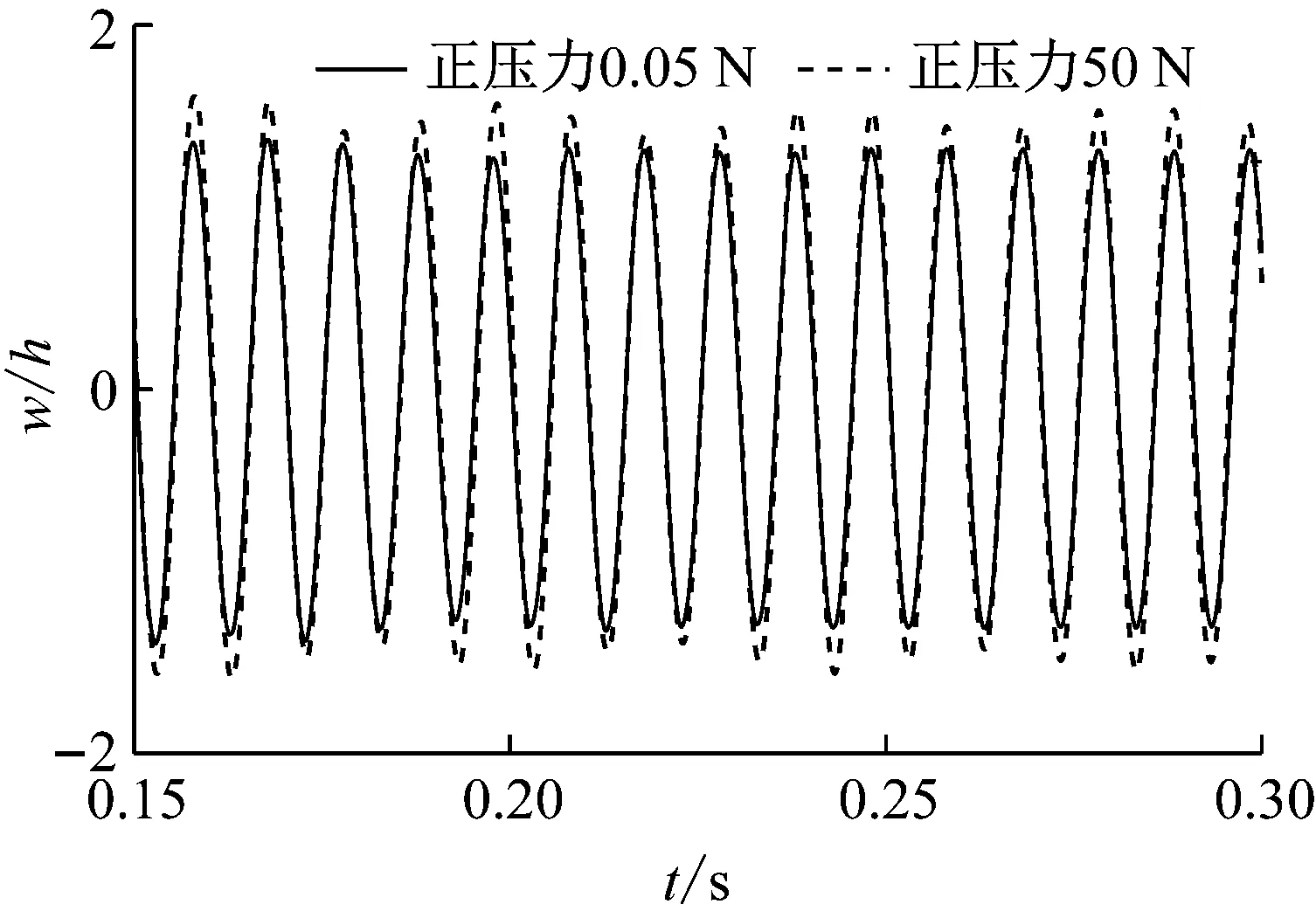
图9 不同正压力条件下壁板的位移响应(SPL=0, λ=330)
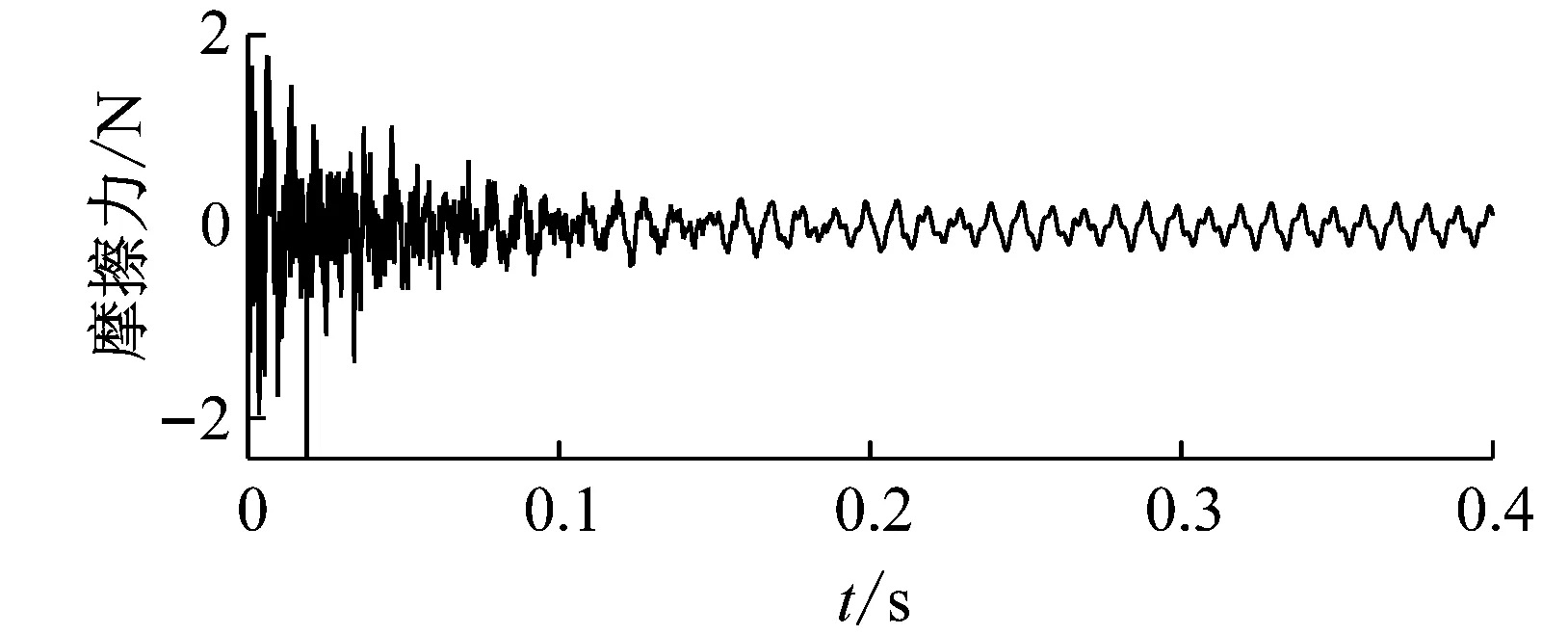
(a) 正压力50 N
下面考虑噪声载荷与气动载荷联合作用下的壁板非线性振动响应。图11给出了噪声载荷和无量纲动压分别为120 dB和λ=330时的摩擦力曲线。结果表明,相较于仅有气动载荷作用的情况而言,处于黏滞状态的摩擦力变得十分复杂,具有随机性。图12给出了x=0.15 m,y=0.25 m处的层合板横向振动位移响应。从图中可以发现,由于正压力为5N的摩擦边界上存在滑动摩擦,其耗散了壁板振动的能量,壁板的横向振动位移响应相对于完全黏滞状态有所减小。对比图9的结果可知,图12中由于摩擦边界滑移削弱的层合壁板振动响应程度较小,这一方面是因为强噪声载荷的引入使得摩擦力甚至气动载荷对壁板振动的影响减弱;另一方面,统计两种载荷条件下滑移状态占整个时间历程的比例可以发现,图9所示的运动有97.1%的时刻存在滑移运动,而图12所示的运动仅有2.1%的时刻存在滑移运动。
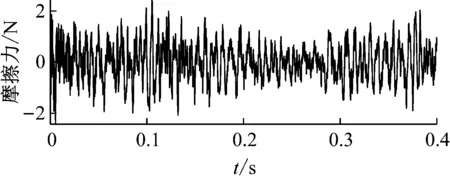
(a) 正压力50 N
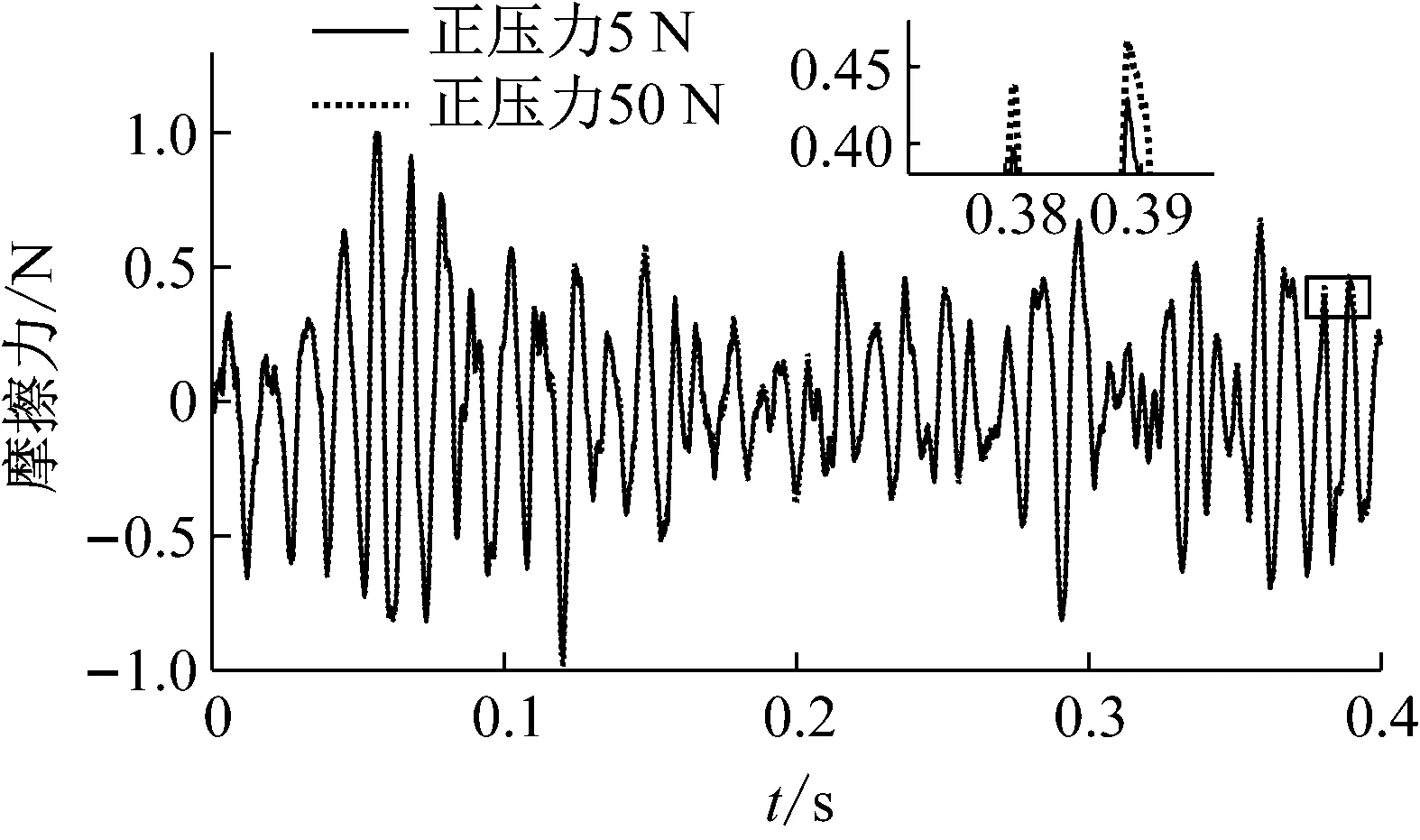
图12 不同正压力对位移响应的影响(SPL=120 dB, λ=330)
3 结 论
本文建立了强噪声载荷作用下含摩擦边界复合材料壁板的气动弹性非线性动力学有限元数值计算模型。利用Reddy三阶剪切变形锯齿理论结合von Karman大变形理论建立壁板的非线性结构模型。采用高斯限带白噪声、一阶活塞理论和宏观黏滑模型分别计算噪声载荷、气动载荷和摩擦边界上的摩擦力。结果表明:
(1) 在不同气动载荷和声载荷的联合作用下,壁板的振动响应会呈现出由气动载荷主导的极限环运动特征和声载荷主导下近似服从正态分布的随机振动;
(2) 摩擦边界上过大的正压力使得摩擦边界的运动状态处于完全黏滞的状态,减小正压力会导致临界摩擦力的减小从而使摩擦边界上存在耗散振动能量的滑移运动状态,从而对层合壁板的振动位移响应产生抑制作用;
(3) 含有强噪声载荷作用的情况下,相对较小的摩擦力对壁板响应的影响较弱,同时占比较少的滑移状态也使得摩擦力对位移响应的削弱作用很小。
