换流变阀侧套管振动模态及其法兰根部应力研究

2021-07-14赵莉华蔡维哲黄小龙任俊文贾利川

振动与冲击 2021年13期

赵莉华, 蔡维哲, 黄小龙, 任俊文, 贾利川, 王仲

(四川大学电气工程学院，成都 610065)

高压直流输电技术因自身低造价、高可靠性优势，已成为我国输电系统的关键组成部分，而换流变压器作为连接交流系统与直流系统的关键设备，其部件的损坏会直接影响系统的正常运行。作为支持换流变压器稳定运行的核心元件，套管保证了换流变压器进出线的绝缘并避免环境对导电杆造成损伤。换流变压器阀侧直流套管常采用干式复合绝缘(RIP)套管，该套管以铜/铝管为导电杆，环氧树脂浸纸电容芯子为主绝缘，空气侧采用硅橡胶外护套作为外绝缘，主绝缘与外绝缘之间填充SF6气体，油侧套管插入变压器油中[1]。这种干式套管的绝缘性能和阻燃性能相对优于油纸式绝缘套管，更适合用于高绝缘裕度要求的高压直流输电环境[2]，复合材料套管的抗拉、抗弯性能也优于传统的瓷套管[3]。

换流变压器阀侧套管通过安装法兰固定在变压器油箱的升高座上，如图1所示。安装法兰作为套管连接部位，同时也是套管结构的薄弱部位。工作状态下，换流变压器的绕组和铁心会周期性振动，这种振动会传导给阀侧套管，使阀侧套管受到振动载荷作用，相关研究测得换流变压器表面振动信号最大主频幅值约为1.9g、主要频率集中在100～400 Hz[4]。安装法兰承受着套管自重和变压器振动等复杂环境动力，在长期交变应力作用下易在局部高应力区出现细微裂纹，再由微小裂纹逐步扩展，最终出现疲劳破坏，造成换流变压器停运和巨大经济损失。

图1 阀侧套管安装位置

实际工程中已出现多起阀侧套管法兰根部开裂导致绝缘气体泄漏事故，某换流站于2016年发生类似事故，检测后发现多支套管法兰根部与金属筒连接拐角处存在不同程度开裂，表面裂纹如图 2(a)所示。对故障套管拆解后发现，裂缝起始于法兰外侧拐角处，并向内朝着内侧密封槽延伸如图 2(b)所示，裂口存在三个区域：裂纹源、拓展区和瞬断区。这些套管均已使用多年，经分析认为其开裂符合疲劳断裂特征，很可能是长年运行下变压器振动导致金属法兰疲劳断裂。这些裂缝会导致绝缘气体泄漏，而套管内一定压力的SF6绝缘气体对套管起着绝缘保护的作用。当绝缘气体泄漏到一定程度，套管的绝缘性能会严重下降，套管内部发生放电事故，进而危及换流变压器本体的安全。换流变压器通常为超高压或特高压设备，单台价值数千万元以上，一旦因绝缘气体泄漏而损坏则会造成巨额损失。

(a) 套管表面裂纹

结构发生疲劳破坏的主要原因是应力集中，即结构在形状突变位置出现应力局部增大的现象。大量试验研究和理论分析表明，应力集中的部位容易形成疲劳源，在交变载荷的作用下首先萌生裂纹并逐渐延伸，降低结构的疲劳强度[5]。相关研究通常使用结构材料最大局部应力与整体名义应力的比值来描述应力集中，即理论应力集中系数KT，该参数与描述疲劳强度降低程度的缺口疲劳系数Kf呈正相关并在多数情况下服从线性关系[6-7]。理论应力集中系数KT仅与结构形状相关并可以通过有限元方法计算得到,因此有必要对套管的机械特性及法兰根部应力分布进行研究，了解其应力集中情况。

目前对套管机械特性的分析多见于变压器抗震研究领域，研究者通过仿真与试验的方法研究变压器套管机械特性，建立套管的简化有限元模型并分析了其模态特征和模拟地震激励下的响应特性[8-9]。不过相关研究主要关注地震波短期作用过程中套管整体响应特性和抗震强度，没有专门对套管法兰进行详细分析。此外,文献[10]根据相关规范要求，对400 kV直流套管受弯曲、扭转试验载荷时位移和应力进行了简单仿真，验证规范试验条件下套管应力不超过材料断裂应力。文献[11]针对GIS用空心复合套管进行有限元建模，分析了法兰壁厚、加强筋宽度和胶装比对机械强度的影响。文献[12]则针对空心复合套管的铸铝带筋法兰盘进行仿真分析，得到弯矩载荷下法兰盘厚度最优设计为20 mm。综上所述，现有研究对套管法兰根部应力的分析并不十分充分。

为减少金属法兰根部应力集中、降低换流变压器阀侧套管法兰开裂事故发生概率，本文参考实际套管建立阀侧套管有限元模型进行仿真分析，对不同法兰根部结构的套管施加重力载荷并分析其应力分布特征，研究法兰根部结构对应力分布的影响；在套管模态分析基础上采用响应谱方法分析模拟基座振动载荷下法兰根部应力分布特征，研究振动载荷对应力分布的影响。

1 模态与响应谱分析基本原理

1.1 模态分析基本原理

通过模态分析，可以得到阀侧套管的振动特性，即固有频率和振型。将阀侧套管视为一个多自由度系统，其运动微分方程为

(1)

式中：M、C、K分别为套管的质量矩阵、阻尼矩阵和刚度矩阵;{u}和{F(t)}分别为位移向量和激励力向量。

若激励力为0，并忽略系统阻尼的作用，可以得到无阻尼自由振动的运动方程

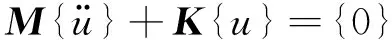
(2)

该方程的解，也就是套管每个质点的位移可以表现为正弦形式

{u(t)}={φ}sin(ωt+φ)

(3)

将式(3)代入式(2)，可以得到：

(K-ω2M){φ}={0}

(4)

其对应的特征方程为

|K-ω2M|=0

(5)

由于M和K均是正定或半正定矩阵，则式(5)的全部根都是正实数或0，这些根是上述方程特征值，也就是套管的固有频率。

通过特征方程得到阶固有频率ωi后，将其带回式(4)，可以得到ωi对应的特征向量，也就是套管的i阶振型列向量{φi}。通过模态分析得到固有频率和振型后可以采用模态叠加方法将实际位移分解为各阶模态的线性组合[13]。

1.2 响应谱分析基本原理

响应谱分析方法是一种特殊的模态叠加方法，通过激励的响应谱和结构的模态进行叠加合并来计算结构承受随时间变化载荷过程中的响应峰值[14]。响应谱分析将基座激励载荷施加到具有不同固有频率和阻尼比的单自由度模型上，得到这些模型的响应峰值与模型固有频率之间的关系即为该激励的响应谱[15]。

(6)

在支撑点固定的情况下进行模态分析得到模态矩阵φ，所有特征模态在支撑点处位移为0，因此这些特征模态表示相对位移。将系统各点相对位移用模态叠加表示为{u}=φq，代入运动方程并左乘φT得到

(7)

由于φTMφ,φTKφ是对角矩阵，阻尼也可以表示为对角矩阵，所以可以将方程组(7)解耦得到如下解耦模态方程

(8)

将支撑运动沿三个正交方向分解

b(t)=bx(t)lx+by(t)ly+bz(t)lz

(9)

矢量lx对所有x方向平动自由度来说，值均为“1”，对所有其他自由度则均为“0”，矢量ly、lz同理。由此得到模态运动方程

(10)

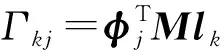
因此，当已得到通过基座运动施加的k方向激励载荷的响应谱时，系统阶模态的响应峰值振幅是相应固有频率下的响应谱值与参与因子(结构属性，与载荷无关)的乘积。

Rkj=Sd(ωj,ζj,bk(t))Γkj

(11)

得到各阶模态的响应值后，为了获得总的响应值，需要将各阶模态响应值按一定的方法进行合并。对固有频率分布比较均匀的结构，可以采用各阶模态响应的平方和的均方根作为总响应(SRSS方法)；对固有频率分布存在集中，即各阶模态具有关联耦合性的结构，则需要采用完全二次方合并方法(CQC方法)进行叠加[16]。

2 换流变阀侧套管模型

2.1 阀侧套管有限元模型

本文根据某500 kV换流变压器阀侧复合套管进行实体建模得到有限元模型如图 3所示，模型主要由导电杆、套管本体、金属法兰三部分组成，忽略均压环、接线端子等附属结构。套管全长7 900 mm，空气侧套管长6 100 mm，油侧套管长1 800 mm，套管外径350 mm，金属法兰及套筒长1 100 mm。套管各部分材料和计算采用的材料机械性能参数如表1所示，复合材料套管本体仅考虑玻璃钢弹性模量20 GPa，并采用考虑其外部包裹硅橡胶伞裙的等效密度，取7 000 kg/m3。取套管整体结构阻尼比为2%，设定套管安装角度为相对水平面30°向上，通过法兰盘靠近油侧面固定在变压器上，忽略法兰盘上的螺栓。以套管轴线在水平面上投影为x轴方向、竖直方向为y轴方向建立坐标系。

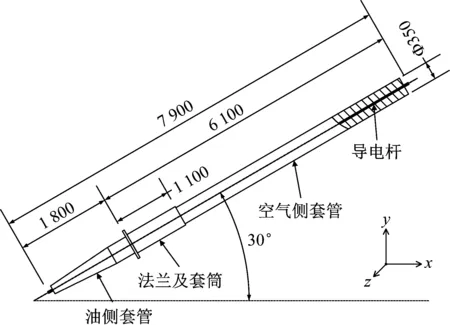
图3 阀侧套管模型示意图

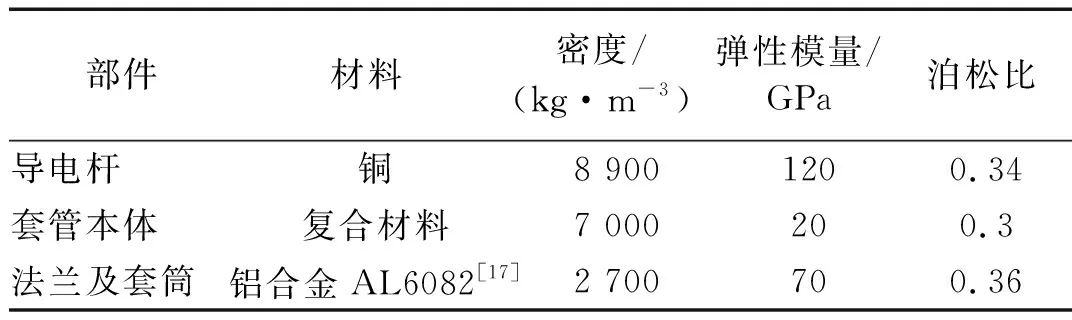
表1 各部件材料机械性能

2.2 套管根部结构

为了解套管根部结构对套管整体变形和金属法兰上应力分布的影响，将法兰拐角的曲率半径和套筒上加强筋的长度、宽度、高度、起始位置作为变量，观察其改变时套管整体变形和法兰应力分布的变化。

法兰套筒上常设置加强筋以增加结构刚度，但受套筒上末屏盒子等结构的限制，仅能在套筒的上下两侧设置长条形加长筋。根据该加强筋可以将套管根部结构划分无加强筋、加强筋未与法兰盘连接、加强与法兰盘连接三种状态，如图 4所示。将套筒中截面上加强筋与套筒连接位置到法兰盘的距离定义为加强筋的起始位置，从该位置起计算加强筋的长度，将中截面上加强筋顶部到套筒圆柱面的距离定义为加强筋的高度，将加强筋两个侧面间距离定义为加强筋的宽度，从而得到长条加强筋长度、宽度、高度、起始位置四个变量，如图 5(a)、(b)、(c)所示。如图 5(d)所示，法兰拐角是法兰盘与套筒之间过渡的连接拐角，作为结构的尺寸突变位置，该位置会用圆角过渡以均匀应力，其曲率半径是影响套管根部应力分布的关键参数。

(a) 无加强筋

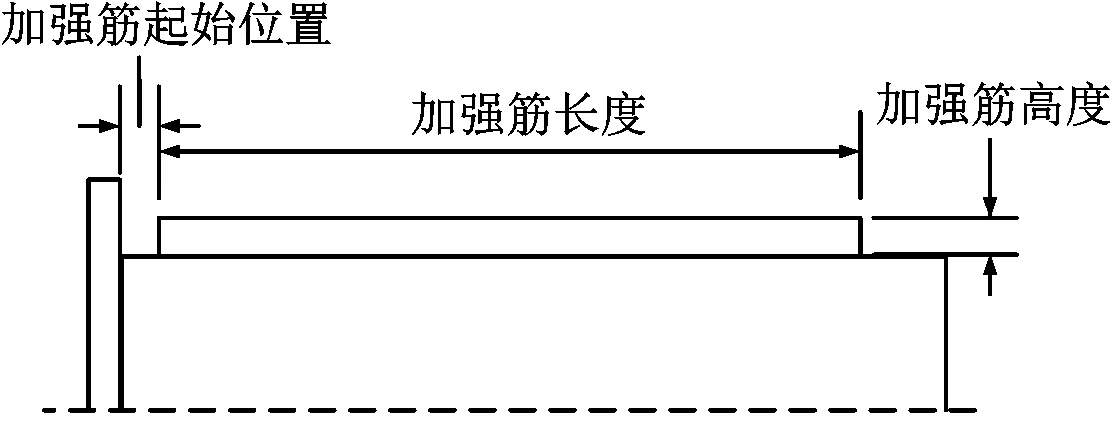
(a) 法兰及套筒侧视图(加强筋未连接)

除长条加强筋外，法兰盘上还可以设置三角形加强筋连接在法兰盘和套筒之间，三角形加强筋在长条加强筋两边对称分布，如图 6(a)所示。将三角形加强筋和套筒中截面的夹角定义为三角形加强筋的安装角度，如图 6(b)所示。设置三种排列方式，即法兰盘平面的每个象限有1、2、3条三角形加强筋，三角形加强筋之间的夹角与安装角度相等，并定义离中截面最远的三角形加强筋与中截面的夹角为最大加强筋角度，如图 6(c)、(d)所示。

(a) 三角形加强筋示意

3 套管根部应力静力仿真

3.1 拐角曲率半径的影响

对阀侧套管受重力载荷，法兰拐角曲率半径从1 mm增加到20 mm条件下计算金属法兰的应力和套管整体变形。曲率半径为2 mm时金属法兰等效应力分布如图 7(a)、(b)所示，应力主要集中在法兰拐角环面的顶部和底部。法兰拐角最大等效应力值和套管整体最大变形曲线如图 8所示，随着拐角曲率半径从1 mm增加10 mm，最大变形值在均值39.44 mm的0.4%范围内轻微波动；最大等效应力值迅速减小并趋于平缓，当曲率半径为6 mm时等效应力减小到最大值的50%，当曲率半径增大到20 mm时等效应力减小到最大值的35%。

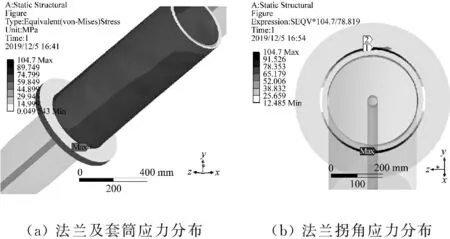
图7 法兰及套筒应力分布(曲率半径为2 mm)

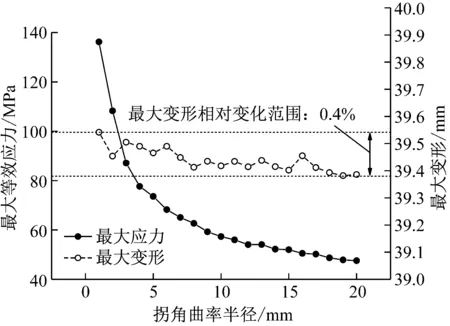
图8 最大应力与最大变形随拐角曲率半径变化曲线

3.2 加强筋长度的影响

对阀侧套管受重力载荷，长条加强筋末端连接法兰盘和不连接法兰盘两种情况下，将加强筋长度从100mm增加到900 mm，计算金属法兰的应力和整体变形。法兰拐角最大等效应力和套管整体最大变形曲线如图 9所示，可以看出加强筋末端与法兰盘连接状态下，最大变形和等效应力都明显小于未连接状态，连接状态最大应力均值为86.9 MPa，相比不连接状态下最大应力均值104.7 MPa减小了17%。当加强筋长度从100 mm增加到900 mm，法兰拐角最大应力值在一定范围内轻微波动，未连接状态下波动范围为均值的4.4%范围，连接状态下波动范围为均值的3.1%；套管最大变形值随加强筋长度增加以近似线性规律下降，未连接状态下降了2.1%，连接状态下降了1.4%。

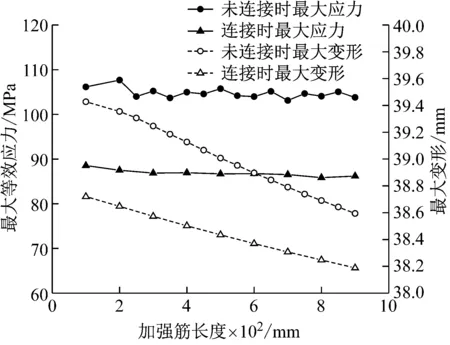
图9 最大应力与最大变形随加强筋长度变化曲线

3.3 加强筋宽度的影响

对阀侧套管受重力载荷，加强筋末端连接法兰盘和不连接法兰盘两种情况下，将加强筋宽度从10 mm增加到100 mm，计算金属法兰的应力和整体变形。法兰拐角最大等效应力和套管整体最大变形随加强筋宽度变化曲线如图 10所示，可以看出当加强筋末端与法兰盘连接，法兰拐角的应力和套管变形均明显小于加强筋未连接状态。当加强筋宽度从10 mm增加到100 mm，除加强筋未连接状态下法兰最大应力缓慢增加了5.04%；加强筋连接状态下法兰拐角最大应力和两状态下的套管最大变形均明显下降，连接状态下最大应力下降了56%，非连接状态和连接状态下最大变形值分别下降了17.5%和27.8%。

图10 最大应力与最大变形随加强筋宽度变化曲线

3.4 加强筋高度的影响

对阀侧套管受重力载荷，加强筋末端连接法兰盘状态下将加强筋高度从50 mm增加到100 mm，加强筋不连接法兰盘状态下将加强筋高度从10 mm增加到100 mm，计算金属法兰的应力和套管整体变形。法兰拐角最大等效应力和套管整体最大变形随加强筋高度变化曲线如图 11所示，当加强筋高度<70 mm时两种状态下套管最大变形相差较小，此后两条曲线差距逐渐明显，而连接状态下法兰拐角最大应力一直明显低于未连接状态。当未连接状态下加强筋高度从10 mm增加到100 mm，套管最大变形减小了3.6%，法兰拐角最大应力在均值102.3 MPa的1.8%范围内轻微波动。当连接状态下加强筋高度从50 mm增加到100 mm，套管最大变形减小了3%，法兰拐角最大应力减小了17.9%。

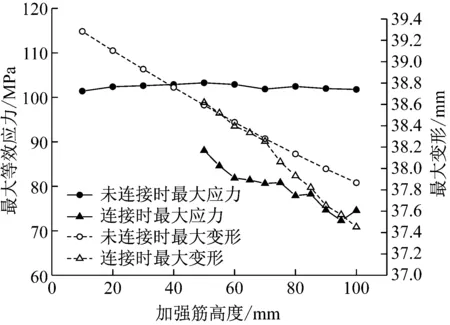
图11 最大应力与最大变形随加强筋高度变化曲线

3.5 加强筋起始位置的影响

对阀侧套管受重力载荷，加强筋末端连接法兰盘和不连接法兰盘两种情况下，将加强筋起始位置从10 mm增加到100 mm，计算金属法兰的应力和套管整体变形。法兰拐角最大等效应力和套管整体最大变形随加强筋起始位置变化曲线如图 12所示，加强筋连接状态下应力和变形均明显小于非连接状态，并且随着加强筋起始位置远离法兰盘，套管最大变形近似线性规律上升，法兰拐角处最大应力先明显下降后趋于平缓，两种状态下曲线变化规律十分相近。当加强筋起始位置距法兰盘距离从10 mm增加到100 mm，连接状态套管最大变形减小了0.12%，非连接状态套管最大变形减小了0.28%，其变化比例接近加强筋长度变化情况下套管响应的变化；非连接状态下套管最大应力先随起始位置增加到50 mm减小到最大值的82.6%后保持平缓，连接状态下套管最大应力先随起始位置增加到50 mm减小到最大值的86.7%后保持平缓。

图12 最大应力与最大变形随加强筋起始位置变化曲线

3.6 三角形加强筋安装角度与排列方式的影响

对阀侧套管受重力载荷，长条加强筋末端与法兰盘连接情况，设置三种排列方式的三角形加强筋并调整其安装角度，计算金属法兰的最大应力。不同排列方式下法兰最大等效应力随三角形加强筋安装角度变化曲线如图 13所示，最大应力值随安装角度的增大明显增加。三角形加强筋排列方式选择排列1时，随着安装角度从10°增加到60°，最大等效应力值增加了25.4%，安装角度超过60°后排列1曲线接近无三角形加强筋时最大应力值并保持相对平稳；三角形加强筋排列方式选择排列2时，随着安装角度从10°增加到40°，最大应力值增加了36.4%，并且安装角度大于35°后排列2与排列1的曲线基本重合；三角形加强筋排列方式选择排列3时，随着安装角度从10°增加到27.5°，最大等效应力值增加了34.7%，并且安装角度大于22.5°后排列3和排列2的曲线基本重合。

图13 最大应力随三角形加强筋安装角度变化曲线

比较三种不同排列方式，可以发现相同安装角度时三角形加强筋数量多的排列方式最大等效应力值更低，安装角度为10°时排列三的最大应力值是排列1最大应力值的81.4%。将排列1与排列2同一安装角度的最大应力值之差作为纵坐标，将排列2下该安装角度对应的最大加强筋角度作为横坐标，得到排列1与排列2间的最大应力差曲线，同理可以得到排列2与排列3之间的最大应力差曲线，如图 14所示。从图 14可以看出，当最大加强筋角度大于65°时最大应力差约等于0，此时角度最大的加强筋对法兰最大等效应力几乎无影响。

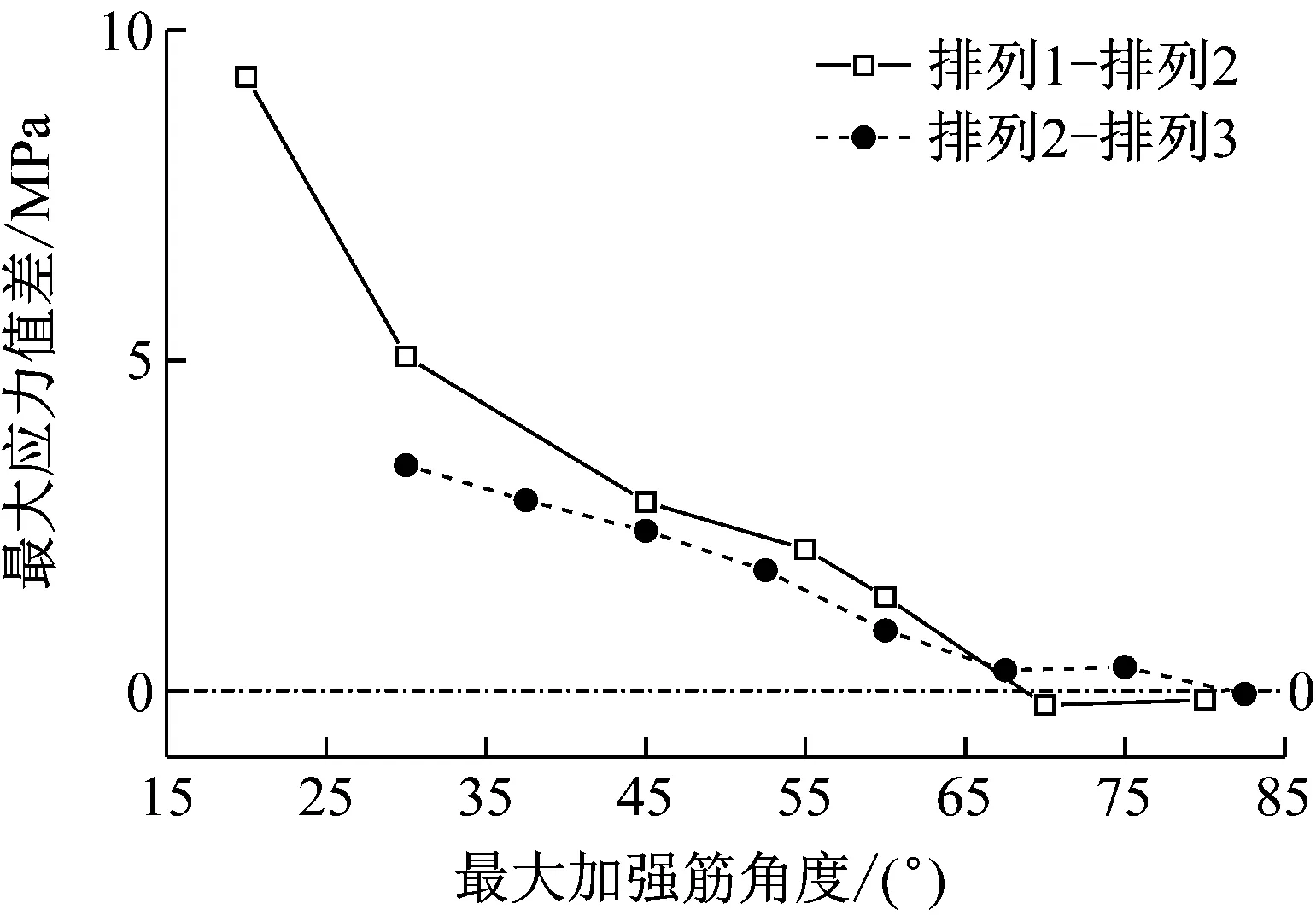
图14 不同三角形加强筋排列方式的最大应力差曲线

4 套管根部应力动力仿真

4.1 套管模态分析

为了解阀侧套管的振动机械特性，对套管进行模态分析，仿真计算套管的固有频率及其对应的振型。在考虑静态载荷预应力的基础上，计算阀侧套管0～50阶模态固有频率如图15所示，套管1阶固有频率为2.935 Hz，套管50阶固有频率为733.8 Hz，前10阶模态固有频率在2～80 Hz范围内。

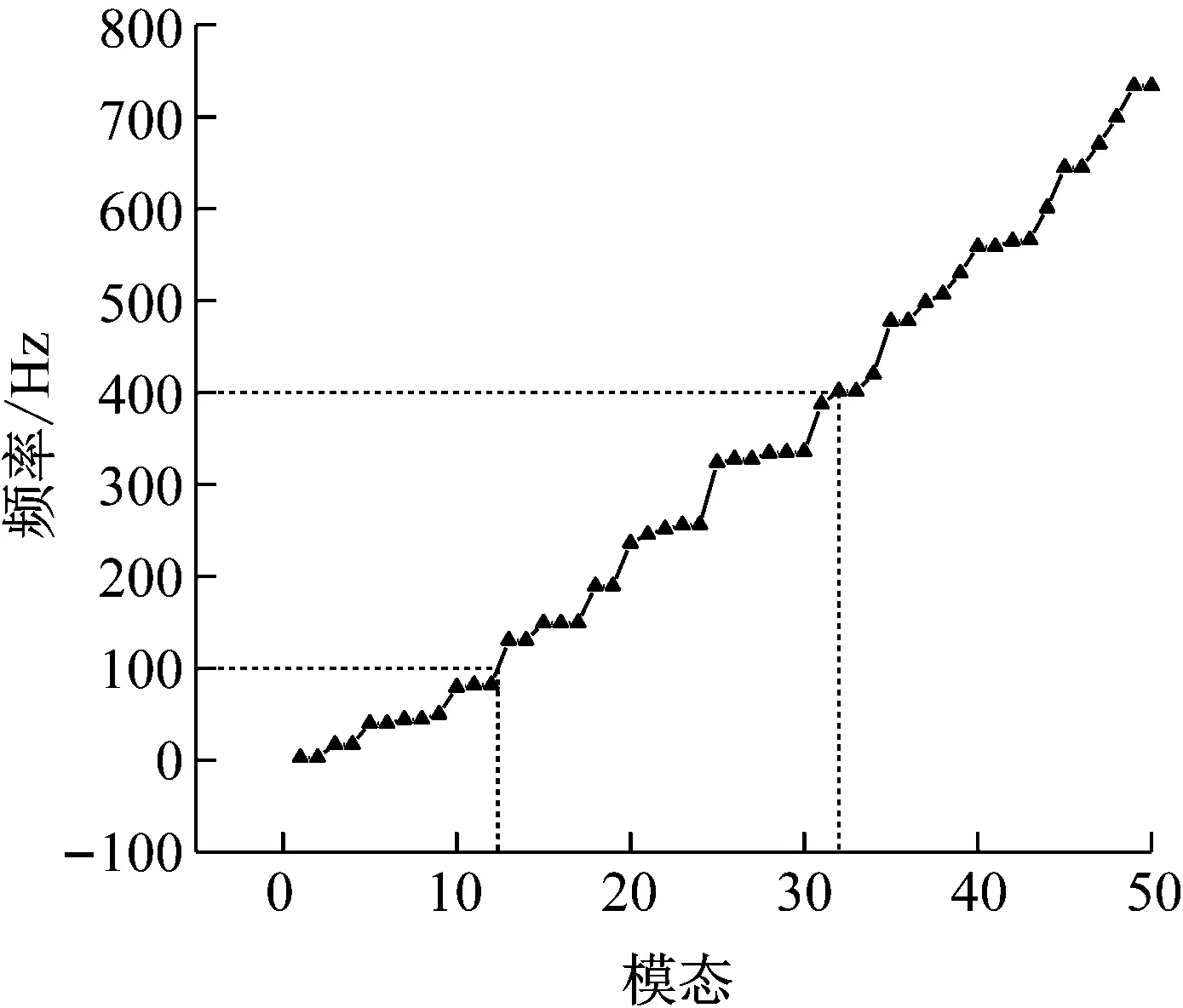
图15 阀侧套管前50阶模态固有频率

从图15中可以看出，套管常常每两阶模态固有频率近似相同、振型相似，区别在于最大振幅位置的振动方向不同。以套管前4阶振型为例，套管1、2阶模态振型类似于套管顶端受径向力状态如图 16(a)所示，套管向一个方向弯曲变形，越靠近套管顶端振幅越大，两阶振型区别在于1阶振型偏向z轴负方向而2阶振型偏向z轴正方向。套管3、4阶模态振型则如图 16(b)所示，套管空气侧中部呈拱形，存在套管顶端和空气侧中部两个振幅较大区域，两阶振型区别在于3阶振型顶端偏向y轴负方向而4阶振型顶端偏向y轴正方向。

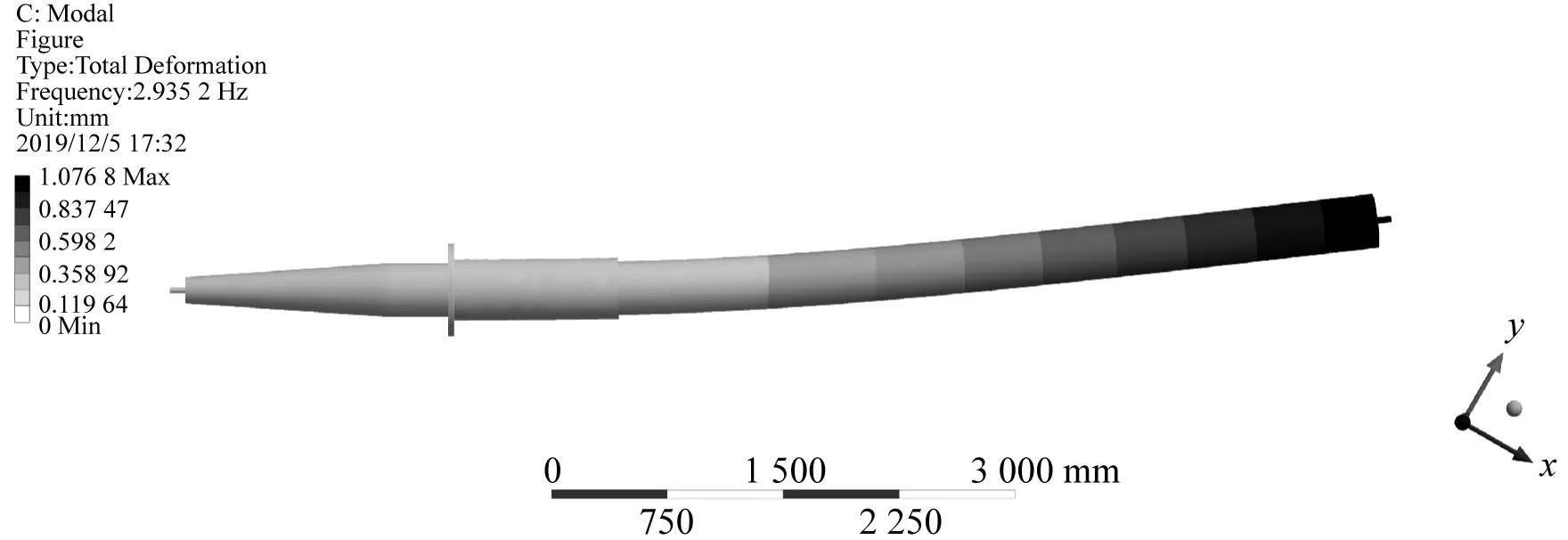
(a) 1阶模态振型

换流变压器振动的主要频率集中在100～400 Hz，而从图15中可以看出，套管的13～31阶固有频率处于100～400 Hz范围内。通过对阀侧套管模型进行谐响应分析，得到套管x轴方向位移的幅频响应曲线如图17所示，该曲线在100～400 Hz范围内有数个峰值。这说明从换流变压器传来的振动载荷会导致套管位移和应力的明显变化，在长期振动载荷作用下，安装法兰拐角位置逐渐出现细微裂纹，最终导致疲劳破坏并在应力集中部位开裂。

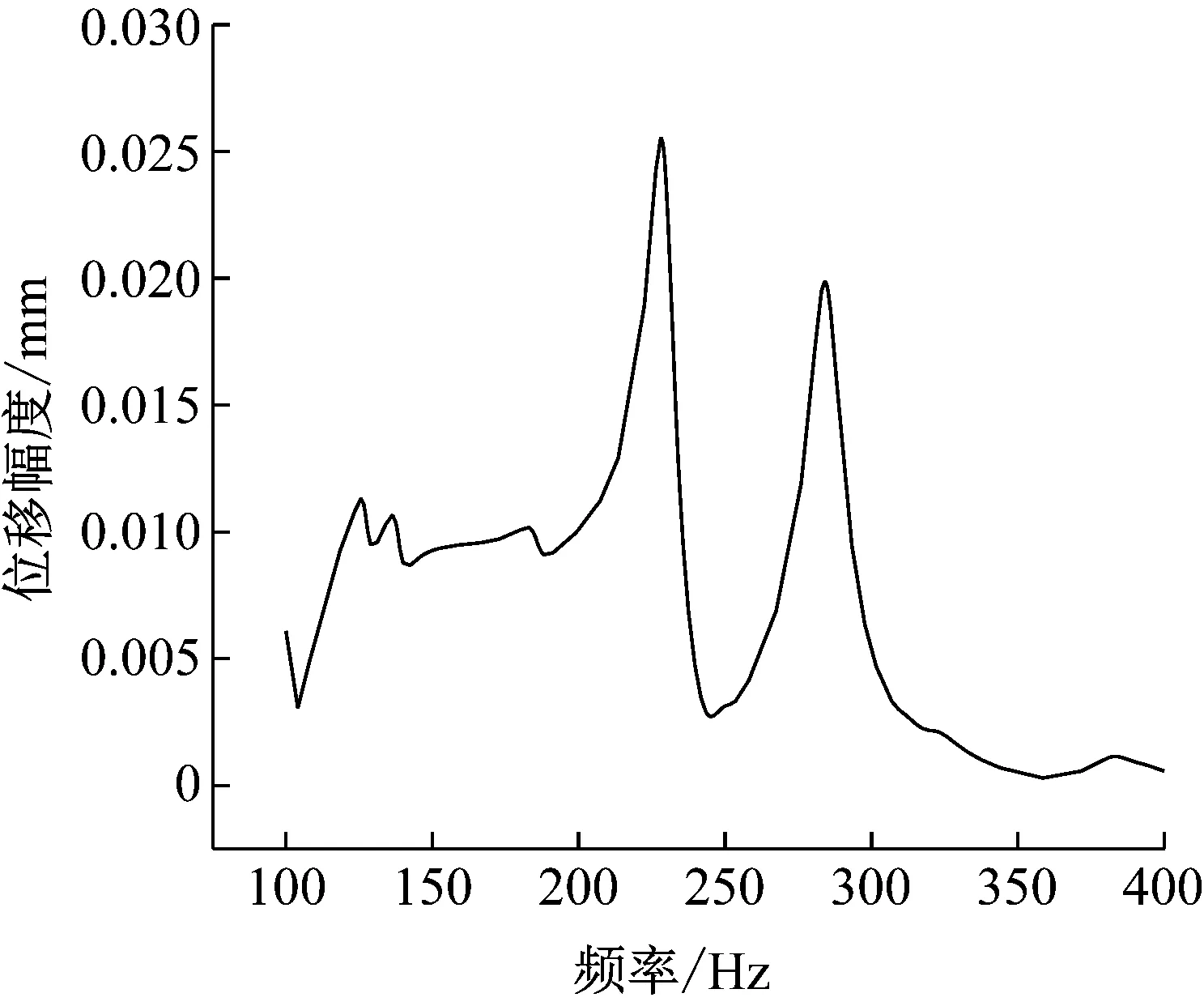
图17 套管位移幅频响应曲线

4.2 套管振动载荷响应谱

由于换流变压器振动信号主要频率集中在100～400 Hz、最大主频幅值约为1.9g，本文设置套管所受加速度激励幅值为2g，振动频率分别为100、200、300、400 Hz，振动方向分别为x、y、z轴方向，以探究不同振动载荷条件下套管的响应。采用Newmark-β法计算不同固有频率单自由度模型受激励时的最大加速度响应值，得到不同振动载荷的加速度响应谱如图 18所示。因为阀侧套管的各阶模态具有一定的耦合性，采用CQC方法将套管模态振型与该激励响应谱值叠加合并得到套管承受基座振动激励的最大响应。

图18 振动激励的绝对加速度响应谱

4.3 振动载荷的影响

通过响应谱方法分析阀侧套管受到基座传来的振动载荷时的最大应力幅值，该载荷振动方向为x、y、z轴方向、振动加速度幅值为2g、振动频率分别为100 Hz、200 Hz、300 Hz、400 Hz。

振动载荷下套管法兰的应力依然集中在法兰拐角位置，如图 19所示。不同根部结构下法兰最大应力幅值如图 20所示，图(a)、(b)、(c)分别代表法兰根部结构为无加强筋、长条加强筋未连接和加强筋连接，横坐标代表不同振动载荷频率、不同颜色的条形代表不同的振动载荷方向。从图 20中可以看出，套管响应随振动频率增加而减小，振动载荷频率为100 Hz时法兰最大应力幅值约为20～22 MPa，高于其余情况。比较套管受不同方向振动时最大应力幅值，发现当振动频率<400 Hz，套管受x轴向振动响应幅值大于y轴方向大于z轴方向，仅当振动频率为400 Hz时套管受x轴方向振动响应幅值小于y轴方向。并且当根部结构为加强筋连接时，套管受z向振动和受x、y向振动的最大应力幅值差别相对另外两种根部结构较小，这是因为加强筋连接结构降低了套管受x、y方向振动时的应力幅值。

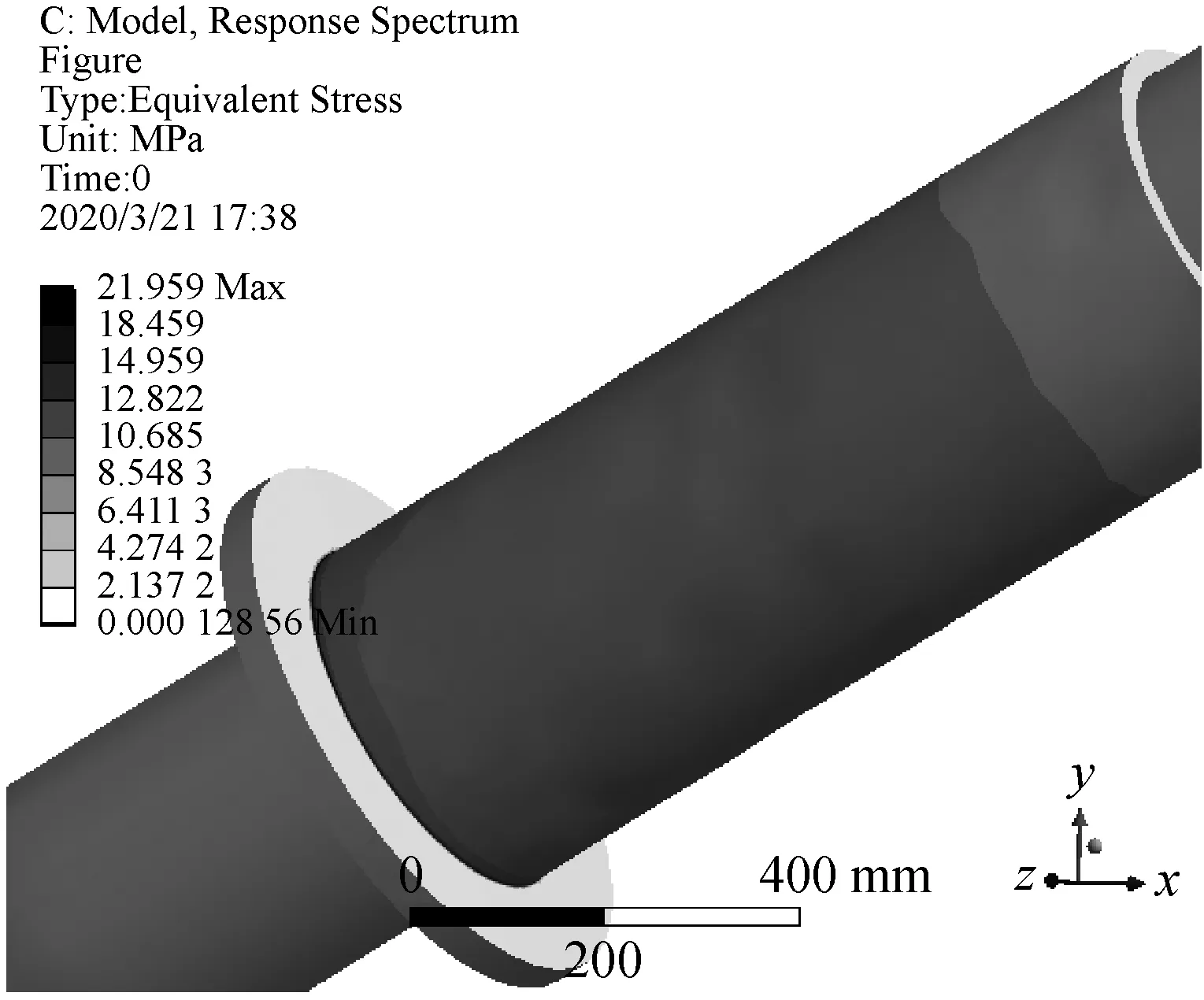
图19 振动载荷下法兰应力幅值分布

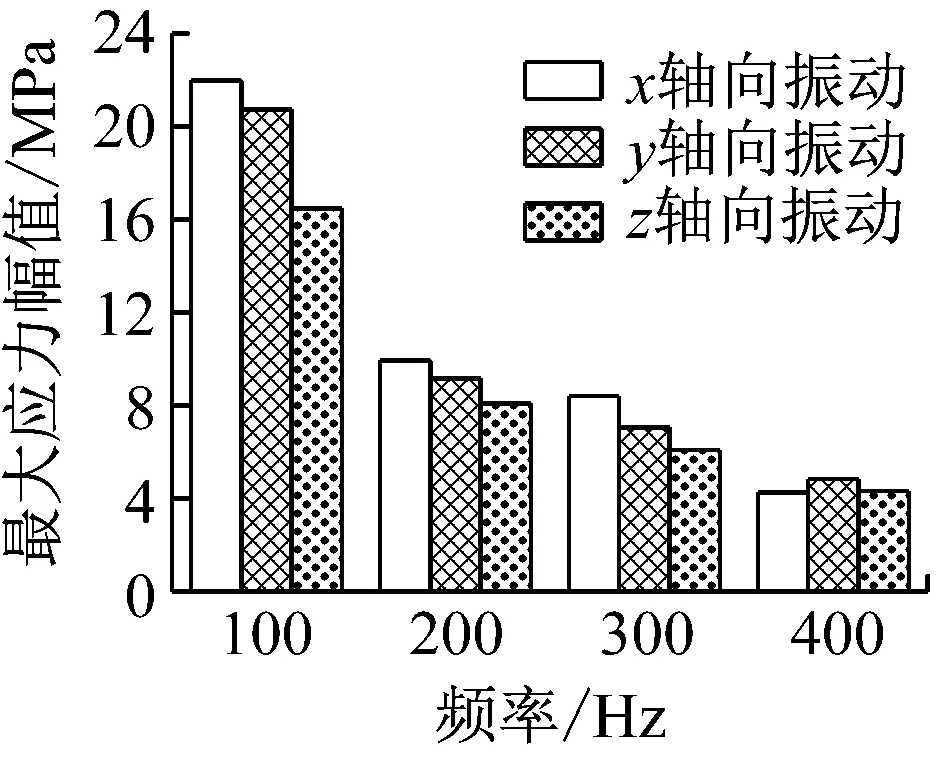
(a) 无加强筋

套管受不同方向振动载荷时法兰最大应力幅值情况如图 21所示，图(a)、(b)、(c)分别代表振动载荷为x、y、z方向，不同颜色条形代表不同法兰根部结构。从图 21中可以看出，加强筋未连接结构下法兰最大应力幅值与无加强筋结构下接近，未连接加强筋对振动载荷下法兰拐角应力没有明显作用；加强筋连接结构下，受x、y方向振动载荷的法兰最大应力幅值明显低于无加强筋状态，但受z方向振动载荷的法兰最大应力幅值与其余两种结构类似。连接加强筋结构对x、y方向振动载荷下套管法兰应力有一定的抑制作用，但对z方向振动载荷下套管法兰应力没有明显影响。