基于双向选择的伪近邻算法
2021-07-14蔡瑞光张德生
蔡瑞光,张德生,张 晓
西安理工大学 理学院,西安710054
分类任务就是通过训练与学习得到一个分类模型,把每个属性特征集映射到一个预先定义的类标号[1]。分类算法[2]是一种应用极其广泛的数据分析方法,在模式识别领域属于监督学习[3]。监督学习是通过一组已知类别的样本,训练出一个目标函数,利用目标函数去判断新数据的类别。近年来,各种分类算法不断被提出,例如,CART[4]、C4.5[5]、RIPPER[6]、KNN[7]、BBN[8]、ANN[9]、SVM[10]等。目前这些分类算法及其改进算法已被广泛应用于商务、医学、科学与工程等领域。然而,随着科学技术的发展和数据收集、数据存储技术的快速进步,随之而来的是数据数量和数据自身维度的大幅度增加,但是数据质量并未得到提升。因此,分类算法在数据分析上面临着更多的困难和更大的挑战,在分类准确率和算法复杂度上往往难以得到满意的结果。
KNN[11]算法是机器学习领域的一个经典算法,其有理论简单、易于实现等优点。该算法首先设置一个参数k,表示近邻样本的个数,然后根据待分类样本到每个训练样本的欧几里德距离,选取距离最近的k个样本作为近邻,最后根据多数投票原则来判断待分类样本的类标号。然而KNN 算法也有明显的不足之处:参数k的设定具有主观敏感性,分类结果受k值影响较大;k邻域中的每个近邻对分类结果的贡献都一样;决策函数只考虑单一的因素,例如多数投票原则或最短距离原则,其分类性能有待进一步提高。
针对KNN 算法存在的不足,Dudani[12]提出了一种典型的距离加权k近邻分类算法(WKNN),该算法的主要思想是不同的近邻对于分类有不同的分类贡献并且真正的近邻点应该具有更多的贡献。Mitani和Hamamoto[13]提出了一种基于局部均值的非参数分类算法(LMKNN),该算法的主要思想是在每一个类中为待分类样本选取近邻,根据每类近邻的局部均值进行分类。Zeng等[14]提出了伪近邻算法(PNN),该算法的主要思想是利用每类中的k个近邻的组合来构造伪近邻,寻找最近的伪近邻进行分类。Gou 等[15]提出了一种基于局部均值的伪近邻算法(LMPNN),该算法作为PNN算法的改进,其思想是将每类中的k个最近邻用k个局部均值来代替,以便找到更加准确的伪最近邻。Biswas 等[16]提出参数无关的模糊加权k最近邻分类算法(PIFWKNN),该算法提出了一种参数独立的模糊k最近邻,并且进一步优化了全局k值。Ertugral 和Tagluk[17]提出了k近邻的改进算法(DNN),该算法是一种基于D近邻点的DNN加权样本方法。
上述几种基于KNN的改进算法虽然都具有较好的分类效果,但是噪声点和异常点对分类准确率的影响并未降到最低,其中LMPNN算法对异常点和噪声点仍然敏感。本文在LMPNN算法的基础上进行改进,提出了一种基于双向选择的伪近邻算法。
1 预备知识
为了方便说明和理解后面的内容,本章主要介绍了LMPNN算法以及互近邻概念。
1.1 符号说明
本文常用的符号整理如表1所示。

表1 符号说明表
1.2 LMPNN算法
在特征空间Rd中,假定训练集有L个类标号ω1,ω2,…,ωL,并且是训练集中类别为ωj的训练样本集合。N和Nj分别代表训练集T中样本的个数和类别为ωj的训练集Tωj中样本的个数。在LMPNN算法中,待测试样本x的类标签通过以下步骤产生:
算法1 LMPNN算法
输入:近邻个数k,待测试样本x,训练集T=类标号ωj(j=1,2,…,L),属于类别ωj的训练集,属于类别ωj的训练样本个数Nj。
输出:待测试样本x的类别c。
步骤1 计算待测试样本x到Tωj(j=1,2,…),L中样本的欧氏距离[18]:

步骤2 将类别ωj中的欧氏距离按升序排列,并取前k个近邻:
步骤3 计算待测试样本x在类别ωj中第i个近邻的局部均值向量:

步骤4 给每一类中的局部均值向量分配不同的权重。在ωj类中,第i个局部均值向量的权值为:

步骤5 计算每类ωj中的伪近邻。

步骤6 预测待测样本x的类标号c:

1.3 互近邻
定义1(互近邻选取准则[19-20])在T*={y1,y2,…,yNj,x}中,给定任意样本yi∈T*(1≤i≤Nj+1),yi在特征空间Rd中的k邻域的定义为:

x的k邻域Nk(x),即为x的k近邻集合,yi的k邻域Nk(yi),即为yi的k近邻集合。若x∈Nk(yi)且yi∈Nk(x),则称yi和x是互近邻。即:
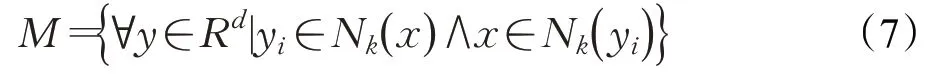
图1 简单清楚地说明了在定义1 下的互近邻的作用。x1的近邻为x2、x3和x6,x2的近邻为x3、x4和x5,x3的近邻为x1、x2和x10,x6的近邻为x7、x8和x9。根据互近邻定义可知,x1和x3为互近邻,将x3加入x1的互近邻集合M。x2和x6为x1的近邻,不是互近邻。
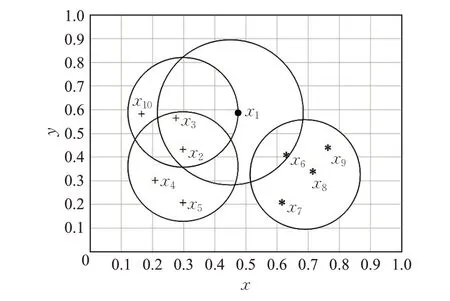
图1 x1 与它的近邻
2 本文算法
通过对LMPNN算法的描述可知,该算法对异常点和噪声点仍然敏感的问题,将影响最终的分类正确率。为此,提出一种基于双向选择的伪近邻算法(BS-PNN),克服异常点和噪声点的敏感性问题,提高近邻集合质量,运用更加符合实际的决策函数。
2.1 改进的类可信度
在图2 中,当决策函数采用多数投票原则时,测试样本1 的近邻个数k取3 时,属于第1 类,测试样本2 的近邻个数k取7时,属于第2类;当决策函数采用最短距离原则时,测试样本1 的近邻个数k取3 时,属于第2类,测试样本2的近邻个数k取7时,属于第1类。对于基于KNN的改进算法,当采用不同的决策函数时,测样样本具有不同的类别,对分类器的精度有一定的影响。在分类算法中,应运用考虑更加全面的决策函数,本文提出了改进了改进的类可信度。概念如下:

图2 测试样本与k 近邻
定义2 设ωj(j=1,2,…),L代表类别,x为待分类样本,为类别ωj中属于x的互近邻,nj为x在类别ωj中的互近邻样本数,且n=n1+n2+…+nL,wi=定义

称其为x对类别ωj的类可信度。
在式(8)中,如果T*(ωj,x)越小,x属于类ωj的可能就越大。为x与类ωj中nj个局部均值加权的平均距离。类可信度T*(ωj,x)由互近邻数和平均加权距离两部分组成。一方面,每类中的近邻个数nj越大,T*(ωj,x)值越小,x属于类ωj的可能性越大;另一方面,每类中局部均值加权距离的平均距离越小,T*(ωj,x)值越小,x属于类别ωj的可能性越大。
本文是将文献[21]类可信度T(ωj,x)中调整为将每类中nj个最近邻用nj个局部均值来代替,并且考虑最近邻的分类贡献。具体分析如下:
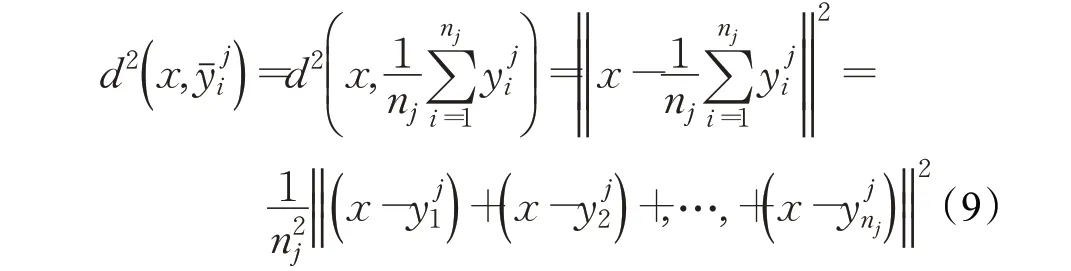
d受单个近邻影响较大,如果近邻集合中含有噪声点或异常点,决策函数受一个近邻点的影响很大,甚至会改变测试样本的分类结果。则运用类均值考虑了所有近邻的分布情况,决策函数受一个近邻样本点的影响较小。在实际应用中,每一个近邻对分类结果的贡献都不一样,应该考虑每一个近邻的权重。在中,wi为每一个赋予不同的权重,距离x越近的局部均值所占权重越大。
本文提出的改进的类可信度综合考虑了每类中近邻样本间的局部均值、加权距离和近邻个数的分类贡献这三个方面,更加符合实际应用。
2.2 基于双向选择的伪近邻算法
在LMPNN 算法中,决策函数采用最短距离原则,选取测试样本的近邻集合时并未识别离群点和噪声点,只是通过加权局部均值在一定程度上减少了异常点对分类结果的影响,异常点对分类器的影响并未完全消除。本文在LMPNN算法的基础上进行改进,提出了基于双向选择的伪近邻算法(BS-PNN)。
BS-PNN算法的基本思想如下:在类别为ωj的训练集Tωj中选取近邻,让测试样本x和训练样本根据互近邻定义进行双向选择,只有当双方为互近邻时,才将训练样本添加进测试样本x的近邻集合Mj(x),互近邻定义可以识别近邻集中的噪声点和异常点,进行双向选择的近邻更加可靠。经过双向选择后,ωj类中测试样本x的近邻个数可能会发生变化,需要重新计算近邻样本数。本文的决策函数从近邻个数和局部均值加权的平均距离两方面考虑,使BS-PNN算法更加符合实际。本文算法的具体步骤如下:
算法2 BS-PNN算法
输入:近邻个数k,待测试样本x,训练集T=类标号ωj(j=1,2,…,L),属于类别ωj的训练集属于类别ωj的训练样本个数Nj。
输出:待测试样本x的类标号c。
步骤1 计算待测试样本x在类ωj中的k个近邻,表示为
步骤4 在Mj(x)中,计算近邻的局部均值距离及近邻个数nj。

步骤5 给每一类中的局部均值向量分配不同的权重。在类ωj中,第i个局部均值向量的权值为:

步骤6 计算每一个类别中的伪近邻。

步骤7 计算改进的类可信度。
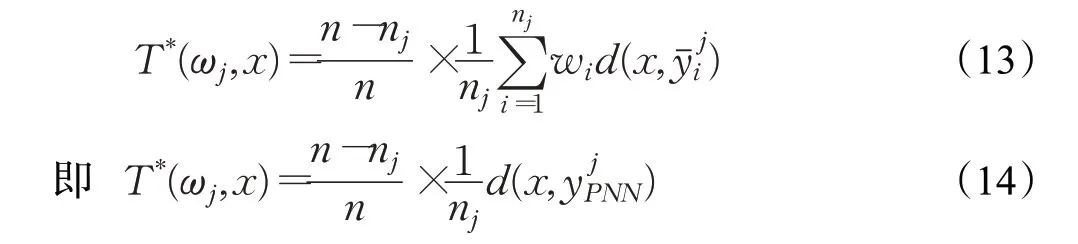
步骤8 预测待测样本x的类标号c:

该算法的流程图如图3所示。
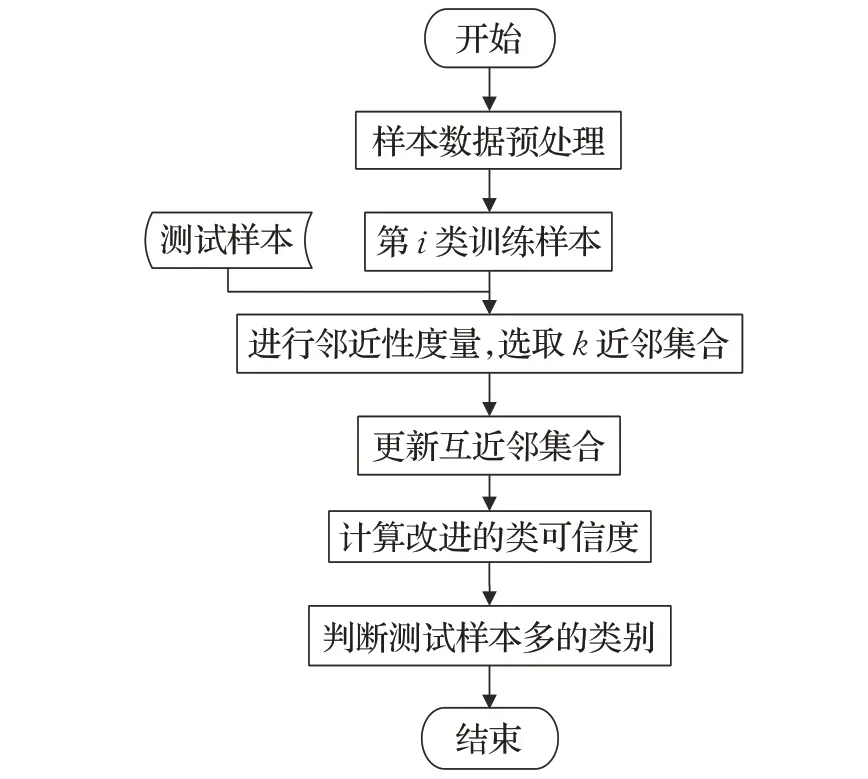
图3 BS-PNN算法流程图
2.3 算法复杂度分析
假设数据集的规模为N,数据维度为d,近邻个数为k,类别个数为L。基于双向选择的伪近邻算法的时间复杂度主要来源于5 个方面:(1)计算测试样例到各个类的距离,时间复杂度为O()Nd+Nk;(2)利用互近邻原理去除噪声样本,并选择有价值的近邻,时间复杂度为O(kdM+2kM);(3)计算每一个类中的局部均值向量,时间复杂度为O(2d);(4)权重ωj被分配给每个类别的第j个局部均值向量,并且找到每个类别的基于局部均值的伪邻居,该步骤要求O()3kM;(5)使用决策函数判别测试样例的类标号,时间复杂度为O()3M。所以总的时间复杂度为O()Nd+Nk+kdM。虽然基于双向选择的伪近邻算法的时间复杂度大于基于改进的KNN分类算法,但是算法在运行时,执行效率较高。
3 实验结果及其分析
为了进一步验证本文所提出的基于双向选择的伪近邻算法的分类性能,在公开数据集KEEL和UCI中选择了15个数据集,在MATLAB R2014a环境下进行仿真实验,并与KNN、DWKNN、LMKNN、PNN、LMPNN、DNN以及P-KNN这7个分类算法进行了比较。
3.1 数据集介绍
本文的15 个数据集中包括3 个规模较大的数据集letter、thyroid 和sparn 和12 个规模较小的数据集bupa、ionosphere、balance、diagnostic、musk、wdbc、wine、iris、dermatology、zoo、vehicle和sonar。
数据集的主要信息见表2,它们分别是数据集名称、名称缩写、样本数、属性数以及类别数。其中数据集的特征维数从4维到167维,类别数从2类到10类,这样可以更有效的验证本文所提出的算法的分类性能。
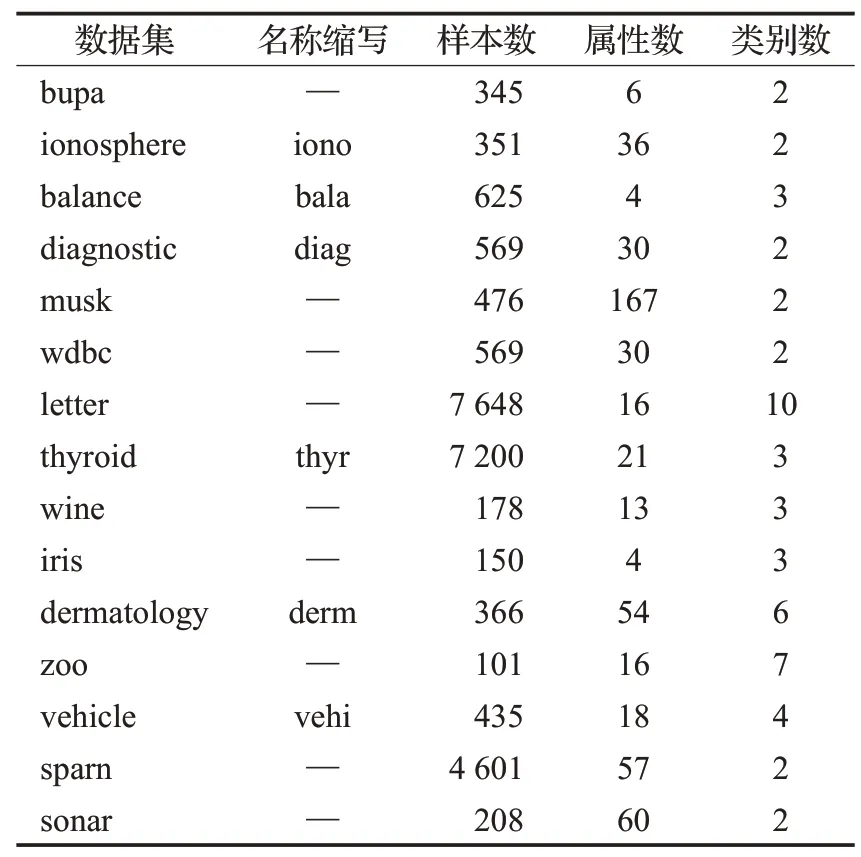
表2 数据集描述
3.2 实验设计和结果
为了验证本文所提出的分类算法的可行性和有效性,以表2 中的数据为实验数据,以分类准确率作为评价标准比较基于双向选择的伪近邻算法和其他基于KNN的改进算法的分类性能。
准确率又称为查准率,是指分类器在测试集中对测试样例进行分类时,正确判断的样本数占总样本数的比例,它反映了分类结果的好坏。其计算方法如下:

其中,A为被分类器准确判断类标号的样本数,B为被分类器错误判断类标号的样本数。
在本文的实验中,均采用m折交叉验证法crossvalidation将数据集随机均等的分为m份,依次拿1份作为测试集,其余m-1 份作为训练集,进行m次交叉验证,并迭代100 次,取平均准确率。根据数据集中样本数量的多少,选择合适的m折交叉验证。当样本数量较小时,选择3 折或5 折交叉验证;当样本数量较大时,选择10折交叉验证。
本文所提出的BS-PNN 算法以及所有对比算法均受近邻个数k的影响。在本文的仿真实验中,对k值采用逐一验证的方法。具体设置如下:首先k的取值范围为1 到15;其次,重复100 次m折交叉验证得到每个k值所对应的平均准确率,将平均准确率最高时所对应的k值选择为最优k值。实验结果都是在最优k值下取得的,如表3所示。
3.3 结果分析
表3中记录了BS-PNN算法与其他7种分类算法在15 个实际数据集上的分类准确率。由表3 可知,除letter、iris 和thyr 这3 个数据集以外,BS-PNN 算法对其他数据集的分类准确率均要高于其余7种算法,尤其在iono、wdbc、wine、vehi和sonar这5个数据集上的分类准确率得到了明显的提升。letter 数据集的最高准确率在LMPNN 分类器上为96.93%,在BS-PNN 的准确率为96.61%,虽略低于LMPNN 和P-KNN 的分类准确率,但仍高于其他6 种对比算法。iris 和thyr 这2 个数据集的最高准确率分别在DWKNN 和P-KNN 分类器上取得,BS-PNN的分类准确率虽略低,但仍高于大多数对比算法的准确率。PIW-LMPNN 在15 个数据集中获得了最高的平均准确率(如图4所示)。

图4 分类算法的准确率均值比较

表3 BS-PNN与其他比较算法的平均准确率 %
本文所提出的BS-PNN算法具有良好的实验表现,可以从以下两方面来解释:一方面,在进行仿真实验时,该算法相对于基于KNN 的改进算法来说,它利用互近邻定义来选择每一个近邻点,让测试样本和近邻样本进行双向选择,在一定程度上可以剔除近邻集合中的噪声点和异常点。因为近邻点对判断测试样本的类别起决定性作用,当近邻点的质量被提高时,分类结果也随之被提高;另一方面,在基于双向选择的伪近邻算法中,经过互近邻定义选择的每类中的近邻个数是不一致的,所以本文在分类准则中,将近邻样本自身信息、近邻样本间的局部均值信息、权重以及近邻样本个数相结合,从近邻样本数量和距离两个方面更加充分地考虑了实际情况,从而提高了分类器的精度。
4 结束语
本文提出了一种基于双向选择的伪近邻算法(BS-PNN)。首先,该算法通过引入互近邻概念来选择测试样例的真正近邻点,然后通过改进的类可信度计算出每一个类与测试样本的相似度,最后通过决策函数得出测试样本的类别。通过在真实数据集和人工合成数据集进行仿真实验,可知BS-PNN算法的分类性能优于其他基于KNN 的改进算法,同时该算法的复杂度类似于LMPNN 分类器的算法复杂度。本文下一步的研究工作,将结合实际问题来进一步探索KNN 改进算法的有效性。
