改进蚁群优化算法求解折扣{0-1}背包问题

张 铭，邓文瀚，林 娟，钟一文

1.福建农林大学 计算机与信息学院，福州350002

2.智慧农林福建省高等学校重点实验室（福建农林大学），福州350002

背包问题（Knapsack Problem，KP）是经典的NP-困难问题，它包括多维背包问题、完全背包问题、分组背包问题和折扣{0-1}背包问题（Discounted {0-1} Knapsack Problem，DKP）等多种类型。DKP 在2007 年首先在文献[1]中提出，它是对商场促销行为的抽象，在商业、投资决策、资源分配和密码学等方面都有实际应用价值。由于DKP是NP-困难的，近几年许多学者对使用智能优化算法来求解DKP进行了深入的研究，如遗传算法（Genetic Algorithm，GA）[2-4]、差分进化算法（Differential Evolution，DE）[5-6]、二进制蝙蝠算法[7]、帝王蝶算法[8-9]、混沌乌鸦算法[10]、蛾类搜索算法[11]、基于群论优化算法（Group Theory-based Optimization Algorithm，GTOA）[12]、细菌觅食算法（Bacterial Foraging Algorithm，BFO）[13]和粒子群优化算法[14]等。由于DKP 提出的时间还不是很长，关于该问题的研究在解的精度等方面还存在极大改进空间。蚁群优化算法（Ant Colony Optimization algorithm，ACO）是求解组合优化问题的经典群智能优化算法，目前尚未发现ACO 在DKP 上的应用研究。同时，现有的算法大多使用价值密度来引导解的优化，单纯使用价值密度来引导解的优化会导致算法过早收敛，影响其寻优能力。针对在DKP 上的以上不足，本文提出了一个改进的蚁群优化（Modified ACO，MACO）算法，算法具备以下几个特征：

（1）根据DKP的构造特点，采用组内竞争方式计算物品的选择概率，从而降低算法的时间复杂度。

（2）在不降低算法精度的前提下舍去启发式信息，从而减少算法所使用的参数，简化参数设置。

（3）采用混合基于价值密度及价值的优化算子，提高算法的寻优能力。

（4）基于上述的改进模块设计出的算法，在DKP问题的求解中具有良好的性能表现。

1 相关工作

1.1 折扣{0-1}背包问题的定义以及数学模型

DKP是一个带约束的组合优化问题，有一个容量为C 的背包和n组物品的集合。每一组i(0 ≤i≤n-1)中包含3 个物品，这3 个物品的价值分别表示为vi,1、vi,2和vi,3，重量分别表示为wi,1、wi,2和wi,3。每组中物品价值与重量之间的关系如下：vi,1+vi,2=vi,3、wi,1+wi,2>wi,3、wi,3>wi,1以及wi,3>wi,2。每一组中至多只有一个物品能放入背包。目标是在不超过背包容量的情况下使放入背包中的物品价值总和最大。由于每组中至多只有一个物品能放入背包，使得该问题有多种编码方式，目前对DKP 的描述有3 种数学模型。Guldan[1]提出了DKP 的第一种数学模型，该模型以0、1方式进行编码，0表示物品不在背包里面，1则表示物品在背包里面。贺毅朝等[2]提出了DKP 的第二种模型和第三种模型。在第二种模型中，以四进制数进行编码，该编码表示每组物品i被选择的物品编号。第三种模型没有指定编码方式，用存储已经放入背包的物品集合表示解，该解只是一个潜在解，只有满足DKP约束的解才是可行解。这里使用文献[2]提出的第二数学模型：

其中，xi表示第i组中放入背包物品的编号，0 表示该组没有物品放入背包。式（2）保证了每一组至多只有一个物品放入背包；式（3）则保证了放入背包的物品重量之和不会超出背包的容量。

1.2 蚁群优化算法求解0-1背包问题

ACO 算法是经典的构造型群智能优化算法，蚂蚁根据以往蚂蚁所留下的信息素和启发式信息构造解。在开始提出时，ACO 算法用于求解旅行商问题[15]，现在被广泛运用于许多领域优化问题的求解，如旅行商问题[16-17]、路径规划[18-20]和函数优化[21]等。虽然现在还没有ACO算法在DKP上的研究，但是已经有许多ACO算法在其他KP问题上的应用研究。文献[22]针对旅行商问题（Traveling Salesman Problem，TSP）和0-1 背包问题（0-1 Knapsack Problem，0-1KP）等NP-困难问题，提出了一种基于蚁群系统的信息素矩阵优化策略，加速了算法的正反馈过程，有助于最优解的探索。文献[23]将ACO 算法运用在0-1KP 上，将问题表示成相应的构造图，并根据该图设计状态转移公式，蚁群根据该公式在图中移动至死亡，所经过的路径成为问题的一个解，在这其中还加入了禁忌列表存放蚂蚁所经过的线段，避免冗余。文献[24]将量子计算与ACO 算法相结合对0-1KP 进行求解。把量子计算中的态矢量和量子旋转门加入到ACO算法中，达到加快算法的收敛速度，并且加入了量子交叉策略，避免了算法过早的陷入局部最优。该文还利用MapReduce 模型实现算法的并行化。文献[25]将ACO 算法与拉格朗日松弛混合求解多维背包问题。首先求解问题的拉格朗日对偶问题，获得各对象的拉格朗日价值；再利用KP中核的概念，根据拉格朗日价值构建该问题的核问题，减少了问题的规模，使得问题的求解速度变快。最后利用ACO算法进行种群迭代搜索，在蚂蚁构造的每个候选解中，在保证解可行的前提下，以高价值的物品替换低价值的物品，进行局部搜索，以便进一步提升解的质量。文献[26]利用改进的遗传蚁群混合算法求解多维0-1KP，将遗传算法与ACO算法结合互补。在算法的每次迭代过程中，挑选几只表现比较好的蚂蚁，对它们进行遗传算法搜索，并将该结果反馈回蚁群，为其他蚂蚁的寻优提供了一个指引。在ACO 算法的迭代过程中加入了轮盘赌方式、禁忌表交换和信息素的混沌更新策略，增加了种群的多样性，并保证种群能够有效收敛。

由于目前尚未发现ACO 求解DKP 的研究文献，这里以文献[22]中所描述的求解0-1KP的ACO算法为例，来描述ACO算法的基本思想。τ和η是存储信息素和启发式信息的两个向量，其中τi表示物品i的信息素值，ηi则表示物品i的启发式信息。在构造解的每一步，蚂蚁根据信息素与启发式信息，对每个还未放入背包的物品用式（4）计算选择概率，然后通过轮盘赌策略选择放入背包的物品。

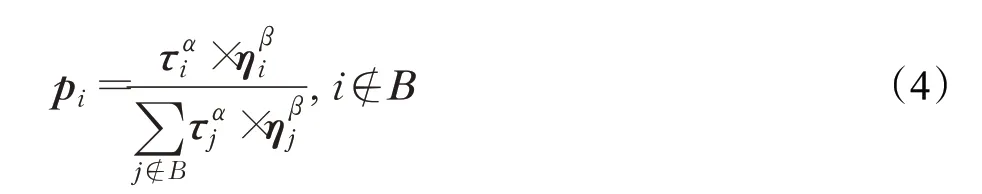
其中，α与β是两个参数，用来控制信息素与启发式信息的重要性，启发式信息用vi/wi表示，B是一个集合，存放已经放入背包的物品。

使用以上的方法来构造解是一个全局竞争的选择，每一个物品与其他未放入背包的物品竞争选择。该选择过程的最坏时间复杂度计算如下：在第i步，要计算n-i+1 个选择概率。每只蚂蚁构造一个解总共要计算次选择概率。所以构造一个解所需的最坏时间复杂度为O(n2)。

当蚂蚁构造完一个解或者所有蚂蚁构造完解时，信息素也要随之更新。在文献[22]中，所有蚂蚁构造完解后，信息素根据当前代的最好解的适应值进行更新，如式（5）所示：

其中，ρ是信息素蒸发率，Δτi是第i个物品上的信息素的数量，其表达式如下：

其中，B表示常数，bs表示当前代所取得的最优解。bsi为1表示在解bs中物品i在背包里面。

1.3 DKP的修复与优化算子

DKP一共有3种数学模型，由于第二种数学模型的编码方式，使得第二种数学模型的存储空间是第一种数学模型的1/3，同样通过该模型编码的解不会违反式（2）。在文献[2，5-6，12-13]中都是使用DKP的第二种数学模型。文献[2]首次使用群智能算法求解DKP，并提出了DKP的第二种数学模型和第三种数学模型。这篇文章使用了遗传算法，针对DKP的两种数学模型，提出了第一遗传算法（FirEGA）和第二遗传算法（SecEGA）来求解DKP，并分别采用修复优化的方法提高解的质量，其中FirEGA 取得更好的结果。文献[5]使用DE 算法求解DKP，采用的方法是对选择操作进行优化：如果两个个体都是可行解，选择适应值高的个体进入下一代；如果两个个体，一个是可行解，一个是不可行解，选择可行解进入下一代；如果两个个体都是不可行解，选择违反约束程度较低的个体进入下一代。对不可行解不进行修复。但是该文章没有使用DKP 的4 种测试用例进行测试，而是随机生成测试用例，所以没有与其他的论文进行比较。文献[6]使用DE 算法求DKP 的第一种数学模型和第二种数学模型，对于第一种数学模型，分别提出混合编码的二进制DE（Binary DE with Hybrid encoding，HBDE）算法和第一离散DE（First Discrete DE，FDDE）；对于第二种数学模型，提出第二离散DE（Second Discrete DE，SDDE）算法，并根据编码方式的不同采取修复优化的方法提高解的质量，3个算法的性能比较，HBDE 取得更好的结果。文献[12]用GTOA分别求解了3种KP：Set Union KP（SUKP）、DKP和Bounded KP（BKP），这里只关注DKP。该文章将可行解作为群直积的一个元素，利用群直积的乘法和逆运算来实现进化过程，并对不可行解进行修复和优化。文献[13]使用BFO 求解DKP，对DKP 的两种数学模型分别采用二进制编码和四进制编码。为了提高算法的搜索速度，对初始种群进行贪心优化，在两种编码方式下，均对不可行解进行了修复和优化。

对于DKP 的第二种数学模型，在处理违反约束的解时大多用基于价值密度的贪心修复优化策略[2，6，12-13]，如算法1和算法2所示。这里的价值密度以vi,j/wi,j表示，将物品根据价值密度降序排序存放入列表h，其中(hk/3,hk%3+1)表示第hk/3 组的第hk%3+1 个物品。在修复算子中，从尾部开始遍历列表h，如果物品在背包里面，则将其取出，直至背包内的物品重量和没有超出背包容量。在优化算子中，从头开始遍历列表h，在不违反DKP 约束的情况下，将不在背包的物品放入背包，以得到更优质的解。但是这种单一的选取方式在背包装入部分物品之后，会使得那些具有较大价值且重量较大的物品无法进入背包，从而导致算法在得到一个局部较好解后更新困难，而导致算法过早收敛。

2 改进蚁群优化算法求解折扣{0-1}背包问题

2.1 信息素表示和选择概率

蚂蚁在构造解时以式（4）竞争选择每一个物品放入背包的概率，最坏的时间复杂度为O(n2)。但对于DKP，每个物品是否放入背包与其他组的物品没有直接联系反之仅与组内其他物品有直接竞争关系。根据这一特性，适当改造原经典算法中的概率选择公式，可以在不降低算法性能的前提下将蚂蚁构造解的时间复杂度降为O(n)。

DKP要求每一组至多只有一个物品放入背包，根据式（2），每一组物品i的值xi有4种可能：0、1、2和3。每一组独立选择该组的物品放入背包，不与其他组竞争。因此，可以用一个n×4 的矩阵τ来表示信息素，其中τi,0、τi,1、τi,2和τi，3分别表示第i组物品中，不选择、选择第一个物品、选择第二个物品和选择第三个物品的偏好，利用该信息素矩阵，每组物品的选择概率计算如下：

其中，pi存放第i组的4 种选择的概率，根据概率以轮盘赌选择来确定第i组物品的选取，α是调节信息素相对强度的参数。

式（7）所描述的选择概率计算实现了组内选择，即每个物品只和组内的其他物品竞争，并不和其他组的物品直接竞争。通过该公式，每只蚂蚁在构造解时，只需计算选择概率4n次，大大减少了算法的运行时间。在式（7）中，没有使用启发式信息：一方面，对不选择物品的情况很难采用直观的构造方法定义合适的启发式信息；另一方面，不使用启发式信息在保证MACO算法的性能的前提下，减少了算法参数的数量，从而有效地简化了算法的实现。启发式信息的作用主要是在初期可以更好地引导蚂蚁构造出优质解，提高算法的收敛速度，在MACO算法中，因为修复与优化算子可以保证MACO 算法的收敛速度，所以可以不使用启发式信息，而且，如果同时使用启发式信息和修复与优化算子，可能使算法快速陷入局部最小，影响算法的全局寻优能力。

2.2 信息素更新

为了更好地平衡算法的多样性和集中性，使用每只蚂蚁至当前迭代为止所取得的最好的解pb来对信息素值进行更新。在所有蚂蚁构造完解之后，根据式（8）和式（9）更新信息素矩阵。采用最大-最小蚂蚁算法[27]的思想，信息素设定范围为[MINPHE，MAXPHE]，MINPHE表示信息素最小边界值，MAXPHE表示信息素最大边界值，当信息素值超出边界时以边界值替换，防止信息素值过大或过小而影响蚂蚁对最优值的探索。

其中，Δτi是所有蚂蚁在j状态下放置在i项上的信息素的数量，计算公式如下：

其中，K表示种群中蚂蚁的数量；pbk表示第k只蚂蚁到当前迭代为止所取得的最好的解；gb表示整个种群至当前迭代为止所取得的最好的解；函数iif()基于对第一个参数的求值返回第二个或第三个参数。

2.3 解的构造

算法3 是蚂蚁构造解的伪代码。它首先创建一个空解s，s包含3个属性s.x、s.v和s.w.其中s.x是一个n维的数组，每个元素s.x[i]表示所选择的第i组物品，0表示不选取该组的物品，s.w和s.v分别表示放入背包中的物品重量之和和价值之和。

将MACO 与其他群智能算法，如标准ACO[22]和FirEGA[2]、GPSO[14]、GTOA[12]、HBDE[6]和SG[4]，比较这些算法生成新的种群的时间复杂度，K表示种群中的个体数，如表1 所示。因为K与问题规模无关，所以MACO 算法的时间复杂度优于标准ACO，而与其他智能优化算法相当。

表1 MACO算法与其他算法时间复杂度比较

2.4 解的修复和混合优化

DKP是约束优化问题，由智能优化算法生成的解可能是不可行的，现有研究均使用修复优化算子对解进行进一步处理，通过修复优化操作不仅保证了解的可行性，也能提高算法的寻优能力。在现有研究中，对解进行修复优化时，大多都是基于价值密度来决定物品的选取顺序。在文献[28]中对{0-1}KP 的研究发现，混合使用价值密度和价值来决定物品的选取顺序有助于提高算法的寻优能力。受此启发，本文在对解进行优化时，以一定概率使用价值作为物品选取顺序的依据，以提高算法的寻优能力。如算法4所示，算法的3到12行根据价值密度从高到低的顺序选择蚂蚁选中的物品，在计算解的重量和价值时保证解的合法性，在对解进行优化时，算法13行到17行根据概率pd选择是根据价值密度还是价值将降序排序的物品放入列表h，调用算法2，从头开始遍历列表h，在不违反约束的情况下将物品放入背包，使解的质量得到提高。

2.5 MACO算法的伪代码

算法5 是MACO 算法的伪代码，其中G为种群的迭代次数，K为种群中的蚂蚁个数，INIPHE是初始信息素。在5到14行，首先使用算法3构造一个新解s，再用算法4对s进行修复优化，在整个种群都构造完解后，更新信息素。因为算法3 的时间复杂度为O(8×n)，算法4的时间复杂度为O(6×n)，所以5到14行的时间复杂度为O(14×K×n)；第15行的时间复杂度为O(4×K×n)。从5 到16 行的时间复杂度为O(18×K×n)。整个种群要迭代G，所以完整的MACO 算法的时间复杂度为O(G×18×K×n)。

3 实验与结果

DKP有4种测试用例，根据每一组的第三个物品与前两个物品之间的关系，分为不相关测试用例（Uncorrelated test instances，UDKP）、弱相关测试用例（Weakly correlated test instances，WDKP）、强相关测试用例（Strongly correlated test instances，SDKP）和逆强相关测试用例（Inversely strongly correlated test instances，IDKP），每种测试用例中根据问题规模的大小，一共有10个测试用例，在接下来的实验中将以这4种测试用例来进行实验。

在MACO算法中，主要的参数符号及其取值如表1所示。为了公平地与其他算法进行比较，MACO算法与其他算法使用相同的评价次数，以文献[6]为例，该文献设置的种群大小为50，种群迭代次数为3n，所以总的评价次数为150n，MACO 算法种群大小与种群迭代次数跟文献[6]相同。参数MINPHE和MAXPHE的比对MACO 算法多样性与集中性的平衡有重要影响，而它们具体的数值与种群大小、信息素分泌和信息素蒸发率相关，根据实验，将MINPHE和MAXPHE的比设置为0.001，因为种群大小为50，根据式（9），每次迭代最多分泌信息素50，为保证信息素不超过MAXPHE，将MAXPHE设置为1 000，而ρ设置为0.05，同时，为了保证在算法开始阶段有足够的多样性，将信息素的初始值设为5 000，这样，因为当信息素大于1 000时，蒸发的信息素总是多于分泌的信息素，所以，除了开始阶段外，经式（8）修改得到的信息素均不超过1 000，如果经式（8）得到的信息素小于1，MACO 算法将它设置为1。除此之外，另外两个参数α（信息素调节因子）和pd（混合优化策略中选取价值密度的概率）通过组合实验来获得其最优设置。实验中α的取值范围是{0.7，0.8，0.9，1，1.1，1.2}，pd的取值范围是{0，0.2，0.4，0.6，0.8，1}。为了增加算法的通用性，不采用为每一种测试用例选取最好的参数组合的方法，而是选择一组总体性能最好的参数。根据实验结果，当α设置为1，pd设置为0.6 时，MACO算法在这4种测试用例上的总体性能最好。

表2 MACO算法的参数设置

3.1 参数α的影响

为了分析α对算法收敛性的影响，使用3个不同的α值来比较MACO算法的收敛性能，每种测试用例中选取第五个测试用例进行测试，图1 到图4 是最优解的收敛过程。以图3为例，当α的取值为1时，MACO算法取得最好的结果。从算法收敛性方面分析，从这些图中可以看出，参数α对算法的收敛速度有明显的影响。如果α太大，算法收敛速度太快，则容易导致早熟收敛；反之，如果α太小，收敛速度太慢，不利于种群对最优解的探索。而且从图中可以看出，α的取值太小时所得出的结果也很不理想。由此可见，一个合适的α值对算法的性能至关重要。

图1 在UDKP5上MACO算法收敛性与参数α 的关系

图2 在WDKP5上MACO算法收敛性与参数α 的关系

图3 在SDKP5上MACO算法收敛性与参数α 的关系

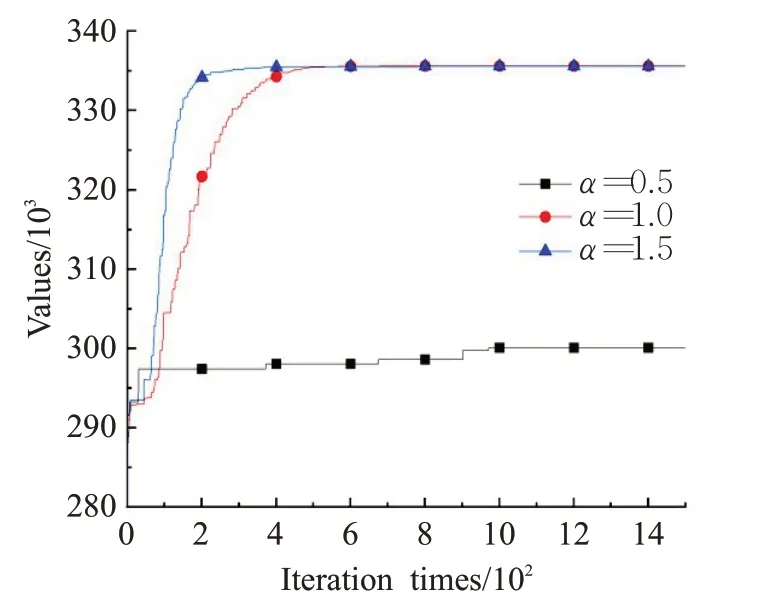
图4 在IDKP5上MACO算法收敛性与参数α 的关系

3.2 参数pd 的影响

为了分析在优化算子中加入价值作为物品选取的依据是否能提高算法的性能，使用每种测试用例的第五个测试用例，以不同的pd值对MACO算法的性能进行测试。pd为0表示在混合优化算子中只用价值作为物品选取的依据，为1则表示只以价值密度作为物品选取的依据。由于问题的规模较大，相对应的解的值也较大，为了更直观地说明所求得的解与已知最优解之间的差距，这里使用解f与最优解f*之间的百分误差（Percentage Error，PE）作为评价解的标准，PE 定义为PE=(f*-f)/f*×100。在每个测试用例上运行MACO算法10 次，图5 到图8 是在4 个测试用例上所获得结果的直方图。从这些图可以看出，尽管在各个测试用例上最佳的pd值是不同的，但相较于在优化算子只以价值密度为依据，只要选取恰当的pd值，均可以提高解的质量。

图5 在UDKP05上MACO算法的性能与参数pd 的关系

图6 在WDKP05上MACO算法的性能与参数pd 的关系

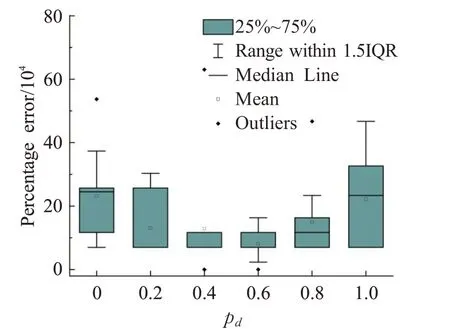
图7 在SDKP05上MACO算法的性能与参数pd 的关系

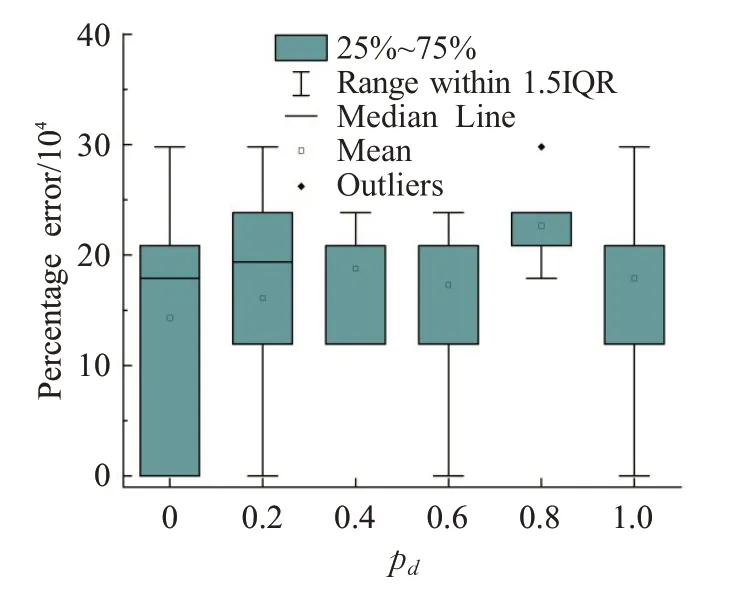
图8 在IDKP05上MACO算法的性能与参数pd 的关系

3.3 MACO算法寻优行为分析

为观察和分析MACO 算法的寻优行为，以每个测试集的第一个测试用例为例，分别比较MACO 与ACO的收敛过程。这里的ACO算法使用1.2节的式（4）、（5）和式（6）来构造解以及更新信息素，并用算法4 来对解进行修复优化。由于MACO 与ACO 的编码方式的不同，在算法4的实现上存在细微的差别。ACO的参数设置为：pd=0.2,α=0.9,β=1，其余参数设置与MACO相同。图9到图12是MACO算法与ACO算法的最优解的收敛过程。从图中可以看出，由于ACO 算法同时使用了启发式信息和修复优化算子，虽然能一开始很快地找到优解，但在之后的迭代过程中就会陷入局部最优，进入停滞状态。而MACO则能在迭代过程中始终保持寻优状态。

图9 在UDKP01上MACO算法与ACO算法的收敛情况

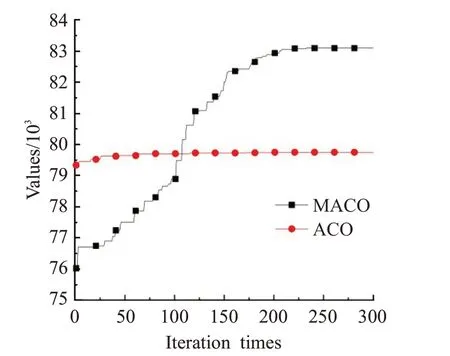
图10 在WDKP01上MACO算法与ACO算法的收敛情况

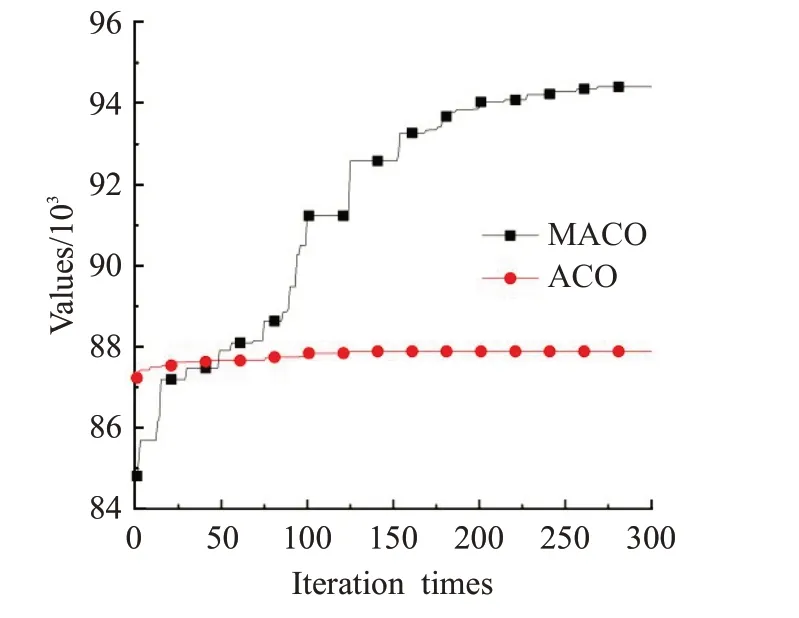
图11 在SDKP01上MACO算法与ACO算法的收敛情况

图12 在IDKP01上MACO算法与ACO算法的收敛情况

3.4 与其他算法的比较

为了观察MACO 算法的竞争性，将MACO 算法与FirEGA[2]、GPSO[14]、GTOA[12]、HBDE[6]和SG[4]进行比较，其实验结果如表3到表6所示。表的Ins、Num和Opt列分别表示DKP 的测试实例、问题规模以及这些测试实例的最佳值。在Result 列中，best、mean 和worst 分别表示各个测试用例独立运行25 次所得到的最好值、平均值及最差值。在这些表格中加粗的数字表示在这6 个算法比较中取得的最优值。

如表3 和表4 所示，在UDKP 测试集和WDKP 测试集上，MACO算法在所有的测试用例上均获得最优的最好值、平均值和最差值；如表5所示，在SDKP测试集上，MACO算法分别在10个、9个和9个测试用例上获得最优的最好值、平均值和最差值；如表6 所示，在IDKP 测试集上，MACO算法分别在9个、8个和5个测试用例上获得最优的最好值、平均值和最差值。为了判断MACO算法与其他算法在性能上是否存在显著差异，使用显著水平为0.05的Wilcoxon秩和检验比较MACO算法和其他算法在所有测试用例上的平均值，在UDKP 测试集上，计算得到的p值分别为0.005、0.005、0.005、0.005和0.005；在WDKP测试集上，计算得到的p值分别为0.005、0.005、0.005、0.007 和0.005；在SDKP 测试集上，计算得到的p值分别为0.005、0.005、0.005、0.005 和0.005；在IDKP 测试集上，计算得到的p值分别为0.005、0.032、0.005、0.007 和0.028。它们均小于0.05，表明MACO 算法显著优于其他5个算法。

表3 在UDKP上的性能比较

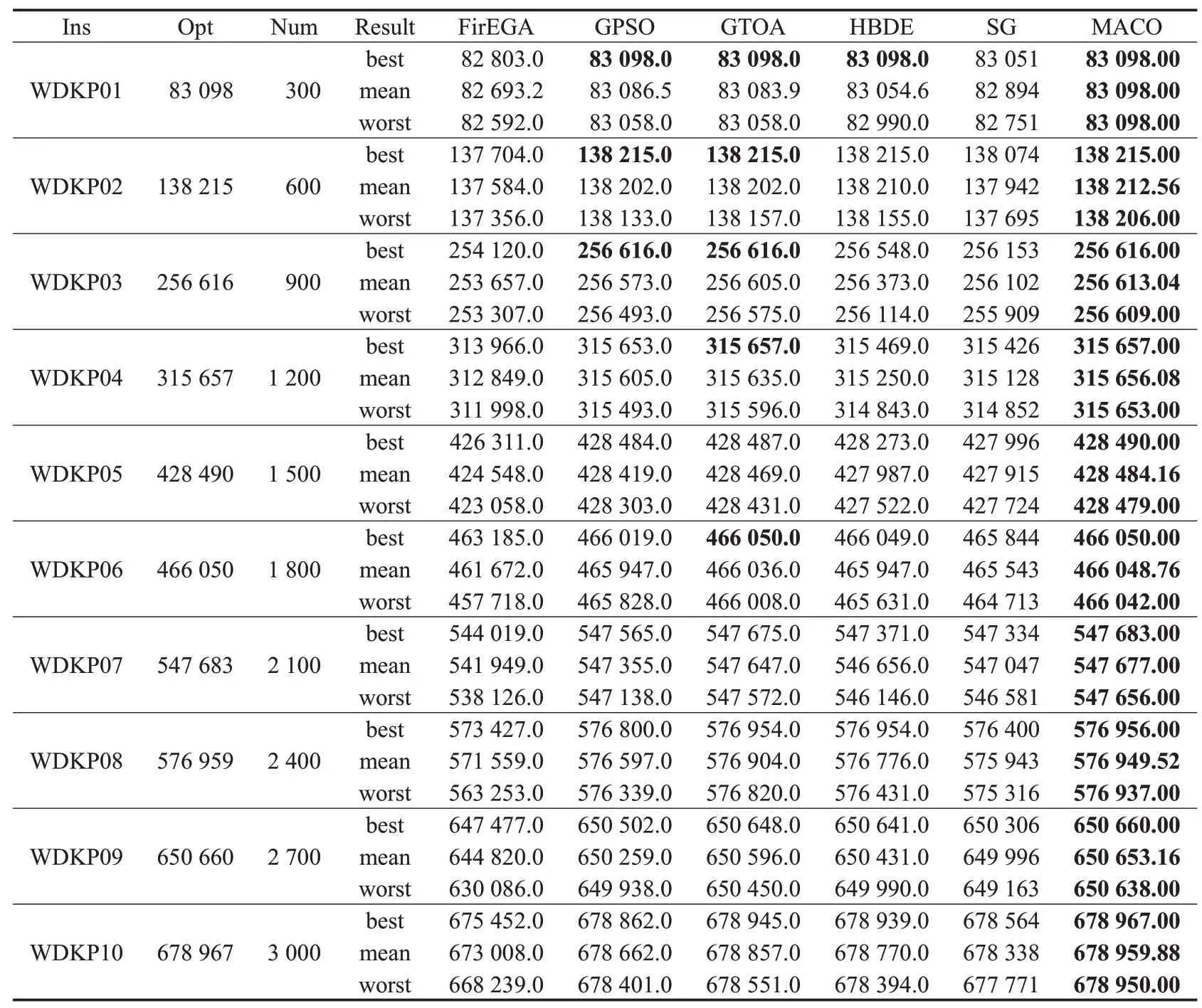
表4 在WDKP上的性能比较

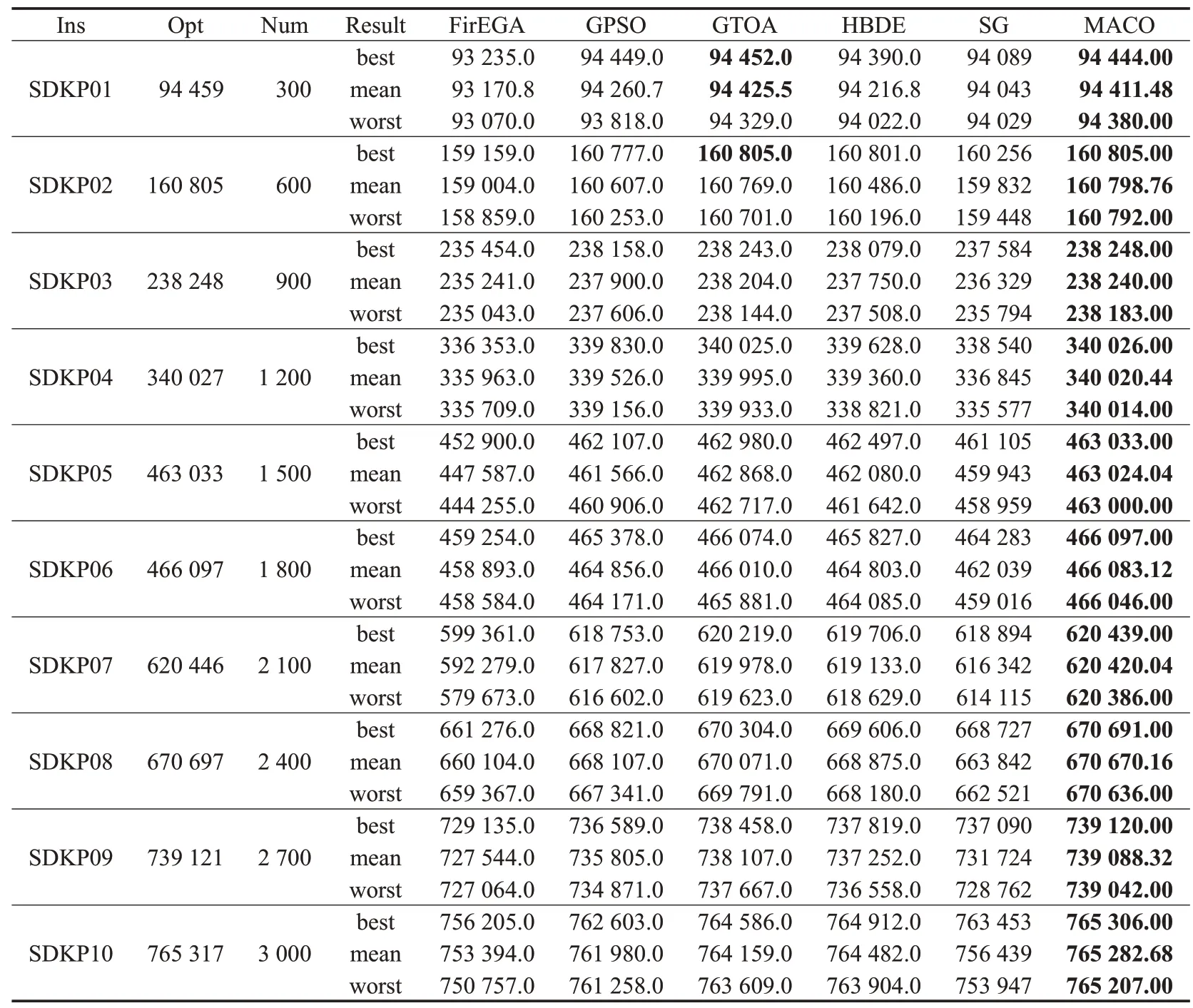
表5 在SDKP上的性能比较

表6 在IDKP上的性能比较

MACO是构造型算法，相较于其他改进型群智能算法，种群能保持足够的多样性，更有利于算法在整个搜索空间中找寻优质区域。可以将修复和优化算子看成局部搜索机制，它有效保证了MACO 算法的局部求精能力。MACO 算法充分利用了构造型算法的全局搜索能力和局部搜索算法的局部求精能力，表现出良好的全局寻优能力。

4 结论

本文提出了一个求解DKP 的MACO 算法，根据DKP组内物品竞争的特点，采用组内选择策略以降低算法构造解的时间复杂性，弃用启发式信息以减少MACO算法参数，从而简化算法的参数调节；MACO 算法使用个体历史最优解来修改信息素，更好地平衡了算法的多样性和集中性。同时，在贪婪优化时中引入混合价值引导操作以提高算法的寻优能力。仿真结果表明MACO算法的性能优于现有其他同类算法。本文提出的混合价值密度引导和价值引导的贪婪优化是一个通用的策略，在今后的研究中计划在改进的MACO 算法及其他同类智能优化算法中，应用该策略去高效地求解更大规模的DKP，并推广至其他相似问题的求解。