大气环境下的LES技术分析

王 俊，黄 依，黄坤荣

（南华大学机械工程学院，湖南衡阳 421001）

0 引言

建筑通风功能主要有满足室内人体基本生理需求、排出室内污染物、消除室内余热的功能，合理的建筑设计可以利用自然通风实现上述功能，从而达到节能减排的目的，CFD技术的发展使其成为了研究自然通风的重要技术手段之一。作为在大气环境下的CFD模拟，RANS往往都不能得到精准的计算结果[1－2]，其原因是大气的湍流表现十分复杂且随机，尽管使用了LES技术，但是仍然面对着如何构造自然风的难点，营造出来的自然风需要体现出大气湍流的特性，这绝非易事。

LES合成入口边界条件主要分为前驱模拟和人工合成湍流两种方式。前驱模拟主要利用周期性循环或者将发展好的湍流流场应用在入口做为边界条件，但耗费的资源比较多，人工合成湍流技术不需要多余的计算代价，已经得到了充分的研究。从原理上来区别它们有：（1）正交分解法（POD）；（2）合成涡流法（SEM），经改进后已经被应用在了多种情况[3－6]；（3）湍流能谱法。前几种方法都不能较好地反映大气湍流特性，对于大气环境下的模拟，湍流能谱法可以从大气能谱来构造湍流，因此具有较好的精度。

1 湍流能谱法

基于一个给定的湍流场，可以用一定数量的正余弦函数叠加而来，Kraichnan[7]最早进行了相关研究，提出了用能谱来构造速度场，并定义了一个速度场，其表达式如下：

当流体为不可压缩时，考虑到连续性方程的约束条件，还需要满足以下关系：

式中：矢量ζn和ξn为在三维或者二维的高斯分布中独立选取的；kn为各项同性分布在随机球表面的矢量。

kn值的不同对应了4个典型的能谱：

式中：k0为随机球的半径；v0为均方根的速度。

当kn为各项同性分布在随机球表面时，遵循E1和E3谱，当kn为从标准差为k0/2、k0/30.5的高斯分布中选取时，遵循E2和E4谱。

2 改进后的能谱法

2.1 RFG法

Random Flow Generation（RFG）由Smirnov[8]提出，该方法考虑了湍流长度尺度和时间尺度，并将它们纳入了速度合成公式中，提高了与空间的相关性。其湍流生成技术分为以下几个步骤。

（1）寻找一个正交变换张量aij，使得给定的各项异性速度相关张量rij对角化：

（2）构造一个中间速度ui，其是正弦和余弦函数的和，且具有随机的相位和振幅。

（3）合成速度场:

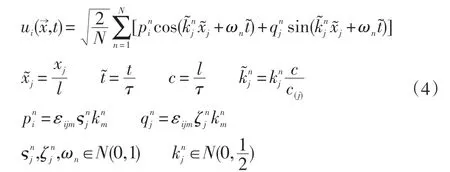
式中：l和τ分别为湍流的长度和时间尺度，可以根据湍动能k和耗散率ε得到，通常可以采用实验或DNS来获得它们；εijm为向量积运算中使用的排列张量；N（M，σ）为平均值为M、标准差为σ的正态分布；knj和ωn分别为样本波数矢量n和湍流能谱的频率。

使用的能谱为：

对上一步生成的速度场进行正交和缩放操作来合成脉动速度，由此可以确定合成的湍流场中湍动能k的大小。

RFG法生成的流场是无发散的，这也是不可压缩流中连续性方程的约束条件，对于均匀和非均匀的流场高阶无发散。该技术由于其合成方法简单、便于实现的特性已经被加入到了Fluent软件中。同样RFG的缺点也十分明显，将l的值取为湍流长度尺度并不能反映出良好空间的相关性，并且其采用的湍流能谱遵循高斯分布，然而高斯谱模型忽略了惯性子程和耗散子程中的能量，在实际中的大气能谱的含能子程中包含了大量的湍流能量[8]，这意味着RFG法的计算结果不能反映真实的流场情况。

2.2 DSRFG法

为了解决上述问题，在RFG法的基础上所改进的湍流能谱法有Discretizing and Synthesizing Random Flow Generation(DSRFG)[9]、Modified discretizing and Synthesiz⁃ing random Flow Generation(MDS－RFG)[10]、Consistent DSRFG(CDSRFG)[11]，后两种方法都是基于DSRFG的一些修正，MDSRFG对DSRFG的时空相关性进行了更新，并添加了修正参数来再现时间相关性；DSRFG生成的脉动速度的相干性与实际大气边界层数据不一致，利用相干函数对长度尺度进行了修正，并更新了DSRFG的频率，此方法为CDSRFG。这里重点讨论的是它们改进依据的原方法本体DSRFG法。

DSRFG由Huang[9]提出，该方法是对RFG法的重大改进，新添加了对齐和重新映射的操作，不仅提出了新的速度合成公式，并且对以往的参数进行了新的定义。该方法生成的速度场为：

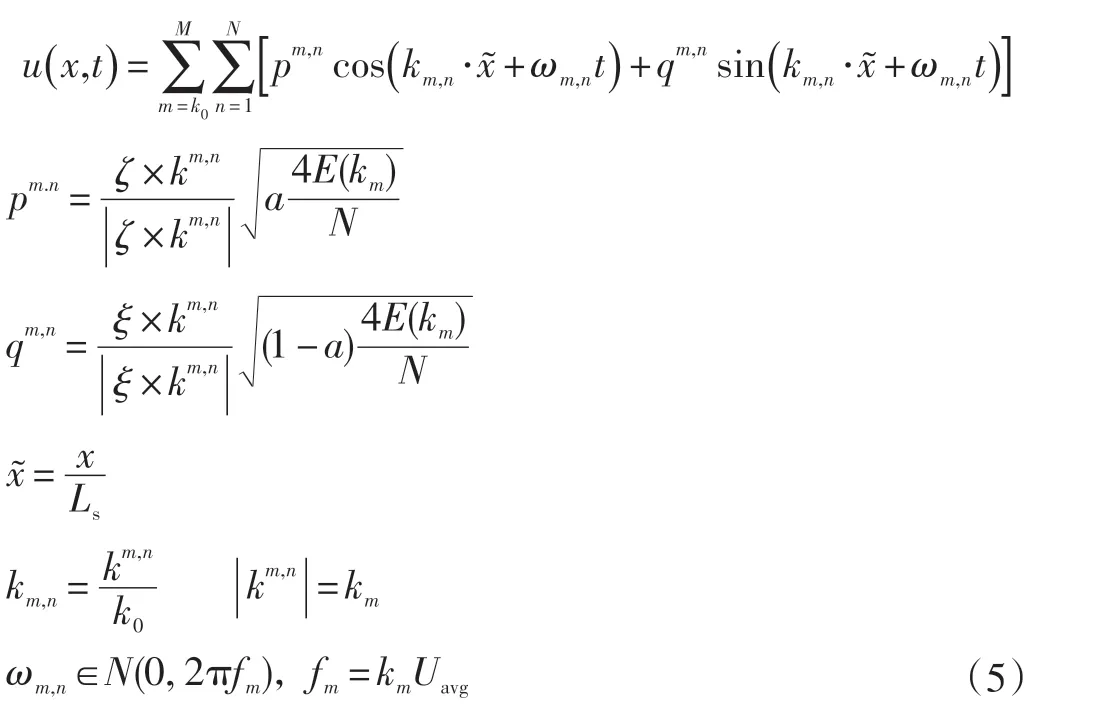
式中：a为均匀分布在0～1的随机数；ζ和ξ为从N（0，1）中随机独立选取的ζ和ξ的随机矢量；N（μ，σ）为标准正态分布，其均值为μ，标准差为σ；km,n为波数；E(km)为湍流能谱；km为km,n随机分布的球的半径即Ls为湍流积分尺度。

各向异性的湍流速度场合成如下。

km,n需要随空间条件不断变换，Huang提出在确定km,n之间，先将pm,n、qm,n能谱沿着主轴对齐，可以使得其分布重新映射在半径为km的球面上。对于给定的能谱E(km)，pm.n和qm.n由如下公式合成：

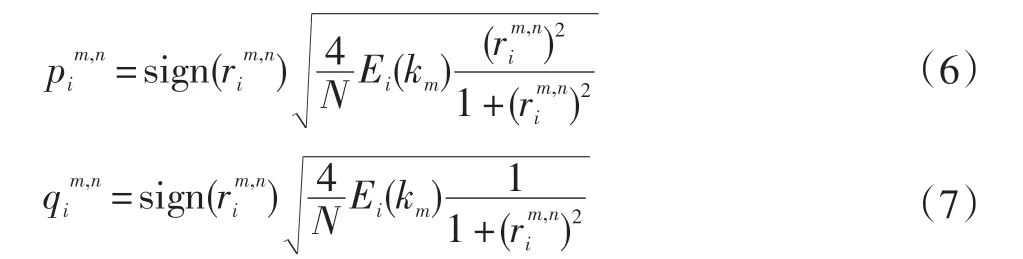
km,n遵循以下关系式：

该方法生成的速度场严格无发散，具有良好的空间相关。Rixin Yu[12]指出尽管上述的几种方法可以解释各向异性，但是空间变化太大导致的不均匀性仍然没有得到很好处理。在不能保证入口边界条件满足无发散约束时，结果精准度会受到影响。

3 新方法推导

根据Rixin Yu的研究[12]，若∇⋅u＝0，则速度场u可以写成势函数形式：u＝∇×ψ，对势函数采用Huang的形式重写：

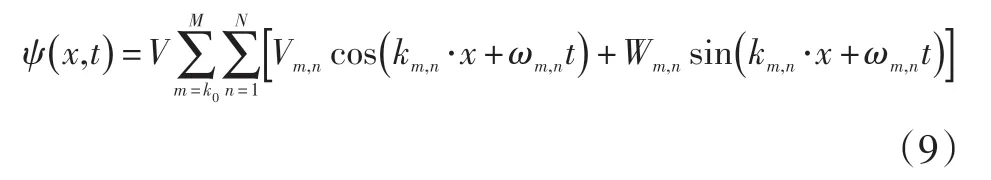
则:

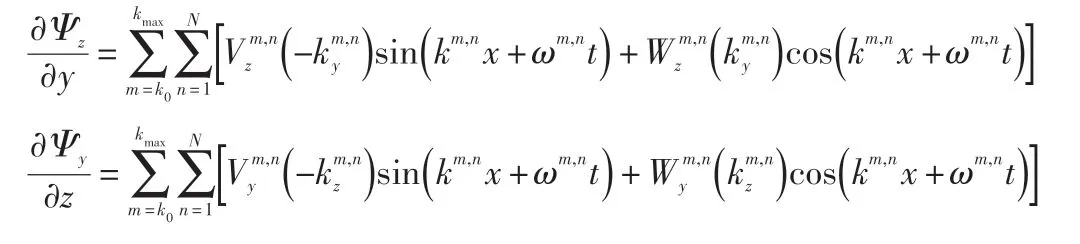
代入得:

其他各个方向速度同理可以得到，因此最终速度为:

设：

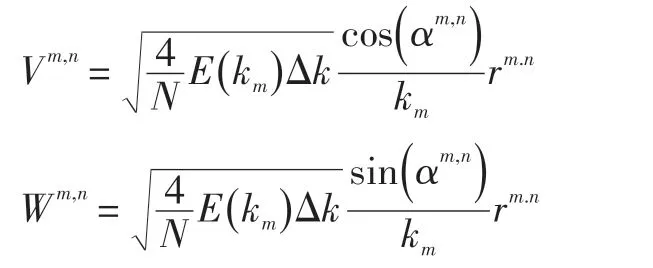
式中：rm,n为垂直于km,n的单位随机向量；km为km,n随机分布的球的半径即| km,n|。

则有：

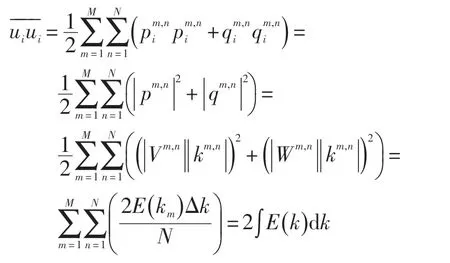
得到的各向同性、空间均匀分布由势函数得到的速度场满足指定的湍流能谱及湍流能量。总结起来公式如下：

式中：ζm,n为均匀分布单位球上的随机向量。

对于各向异性湍流，之前的方法直接改变了各个方向的湍流能谱，也就是式（1）中pm,n和qm,n的方向，这会使得∇⋅u≠0。在上述方法中，pm,n和qm,n的方向平行于ζm,n。为了得到相应的脉动速度分量，可以使得：

对于非均匀湍流，假设式（17）中Vm,n和Wm,n改为垂直方向非均匀分布，则有：

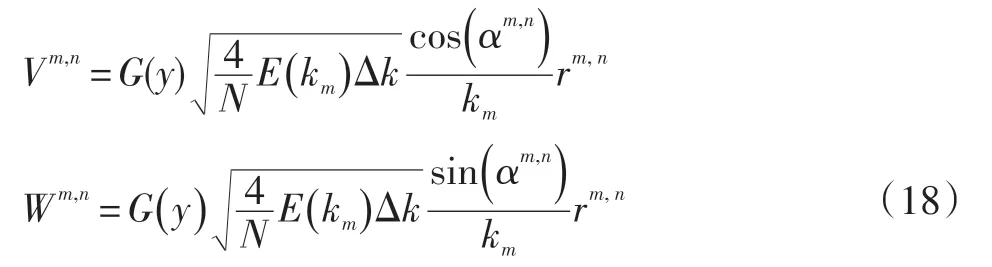
此时速度场为:

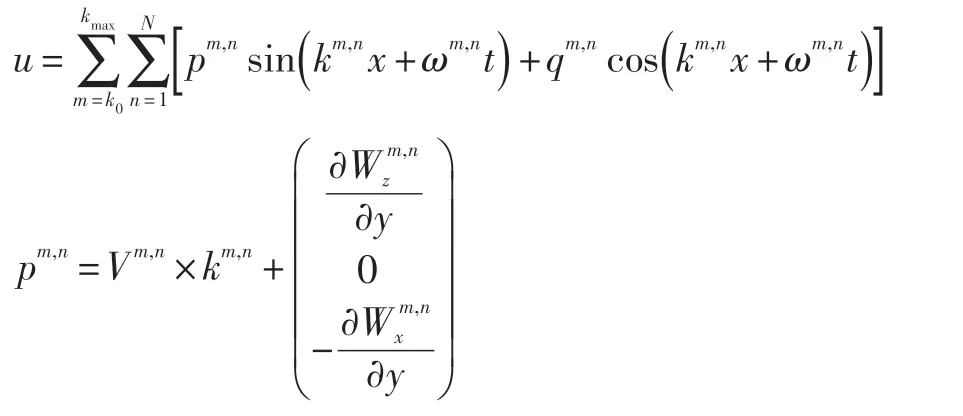
4 渠道流验证

为了体现DSRFG和VPDRFG生成的湍流场差异，分别使用它们生成的湍流场作为渠道流LES计算的入口条件，初始脉动量大小由DNS计算获得[13]，如图1所示，能谱选择修正后的Von－Karman谱，详细可以参考[14]。

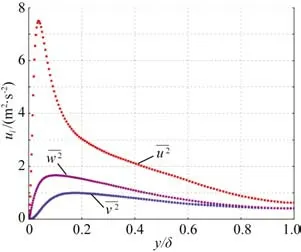
图1 渠道流中各个方向速度脉动量在空间上的分布Figure1 Spatial distribution of velocity pulsation in all direc⁃tions in channel flow

4.1 计算模型的网格

对近壁面处使用了网格加密，如图2所示。DNS计算结果中各个方向速度脉动量在垂直流动方向上的分布，δ为槽道的半高。本次计算分别以实验结果代入不同离散谱方法作为槽道流计算的入口边界，近壁面网格y＋值小于1，不使用壁面函数。

图2 渠道流网格Figure2 Grid of channel flow

4.2 LES计算求解

应用开源软件OpenFOAM进行LES计算，为了便于计算，采用可压缩流LES模型－kEqn（一方程涡粘模型），Ce＝1.048，Ck＝0.026 54，Cs＝0.065，压力项使用GAMG求解，时间项的离散使用Backward（瞬态二阶隐性），其他项采用均二阶精度。时间步长为0.004 s，一共进行了12 000步LES计算。

4.3 结果讨论

图3所示为在Q＝200时，DSRFG与新方法生成的湍流场的差异，可以看出新方法产生了更多的涡结构，在计算时间相同时，DSRFG内的流场发展缓慢，新方法可以更快地重现入口湍流，这意味着使用新方法计算时可以花费更少的总时间步长，节约计算机成本。

图3 DSRFG与新方法的涡结构的比较Figure3 Comparison between DSRFG and vortex structure of the new method

5 结束语

LES技术已经成为了研究建筑通风的重要技术手段，常见的RANS模型由于其“平均”的特性，根本无法得到真实大气环境下的流场情况。本文通过势函数特性对DSRFG法进行了改进，提出了新的方法，该方法严格遵守无发散约束，并且通过渠道流案例比较了它们生成的湍流场的差异。结果表明新方法可以更快地重现湍流，与以往的方法相比，更适用于LES计算。