基于积分解的空间-波数混合域二度体磁异常数值模拟
2021-07-14赵东东赵亚飞周印明王旭龙戴世坤
赵东东, 赵亚飞, 李 昆, 周印明,王旭龙, 戴世坤
(1. 中国地质调查局 南京地质调查中心,南京 210016;2. 中南大学 地球科学与信息物理学院, 长沙 410083;3. 有色金属成矿预测与地质环境监测教育部重点实验室, 长沙 410083;4. 西南石油大学 地球科学与技术学院,成都 610500;5. 湖南科技大学 环境与安全工程学院,湘潭 411201;6. 中国石油天然气集团公司 川庆钻探工程有限公司 长庆井下技术作业公司,西安 710018)
0 引言
磁异常正演数值模拟,是磁法勘探数据定量解释的基础。有关二度体的磁异常数值模拟研究最早是在空间域开始的,Talwani等[1]首次给出了多边形截面二度体磁异常解析表达式;在此基础上,Talwani[2]在计算机上实现了近似二维棱柱状多边形数值模拟;Won等[3]根据泊松关系导出了多边形截面二度体磁异常的解析式,并利用fortran77实现了相关算法,优势在于可以模拟地下任意观测点的磁场;Shuey等[4],Rasmussen等[5]及Cady等[6]在前人研究基础上对原来的算法进行校正,使其能模拟实际地质体所产生的磁异常;贾真[7]系统地推导了均匀多边形截面二度体磁异常及磁异常梯度正演计算公式,并重点探讨了正演公式中所包含的奇异性;Mehdi等[8]采用自适应有限单元法实现了基于拉普拉斯方程的二度体磁异常正演;Adim等[9]在Talwani[2]解析公式的基础上编写了一套基于Matlab的二度体磁异常模拟软件,并提高了数值精度。在频率域,Bhattacharyya[10]推导了任意二度体在频率域的磁场表达式,并进行了反演研究;Pedersen[11]给出了任意二度体、二度半体(以三角形组合为其表面的模型)重磁异常频率域表达式,并指出该公式相对空间域解析公式更为简洁;吴宣志[12]将任意二维物体磁场的波谱解析表达式推广至可用于任意变磁化强度模型;柴玉璞[13]将偏移抽样方法发展为一整套完整的理论体系,有效提升了傅里叶变换的数值精度,使得频率域方法逐渐在处理复杂模型正演问题中广泛应用;吴乐园[14]在偏移抽样理论的基础上,提出利用高斯FFT提高傅里叶变换的数值精度,降低了由于快速傅里叶变换引起的强制周期化、边界震荡效应等影响,并将其应用于频率域二度体磁异常正演模拟,取得了不错的效果。
笔者从磁异常积分表达式出发,提出了一种基于积分解的空间-波数混合域磁异常数值模拟方法。该方法利用高斯FFT[14]将空间域磁位满足的二维积分问题转化为不同波数相互独立的一维积分问题,将一个二维问题分解为波数之间相互独立的一维问题,保留深度方向为空间域,便于浅层网格适当加密,深层网格适当稀疏,兼顾计算精度、计算效率及模拟复杂地形的需要,并采用基于二次插值的形函数实现垂向一维积分,提升积分精度和效率。模型算例中分别设计了突变介质模型和起伏地形模型,首先利用突变介质模型验证了该方法的正确性;其次通过对比分析基于三角函数变化的起伏地形模型磁异常快速算法,与常规积分算法的计算精度与计算效率,验证了起伏地形条件下基于形函数积分的磁异常快速算法的有效性和高效性,并研究了地形起伏最低点与最高点之间剖分节点个数对磁异常场计算精度的影响规律;最后设计非规则复杂模型,研究了不同观测高度的磁异常响应特征。
1 方法原理
1.1 空间-波数混合域磁位
弱磁性体空间域磁位积分公式为式(1)。
(1)
式中:(x,z)和(x′,z′)分别表示观测点和场源任意一点的坐标;U为异常体在空间任意一点产生的磁位;Mx和Mz分别为磁化强度矢量M在x和z方向上的分量;π为圆周率常数;μ0为真空磁导率,μ0= 4π×10-7H/m;如果场源均匀,磁化强度M为常矢量。
对式(1)沿x方向做一维傅里叶变换,得到空间-波数混合域磁异常积分公式为式(2)。
(2)
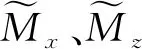
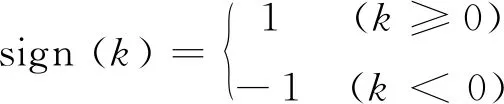
(3)
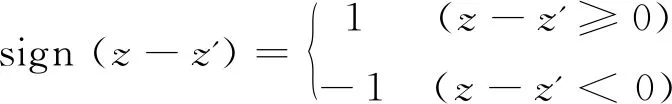
(4)
式(2)即空间-波数混合域磁异常积分公式。对式(1)沿x方向进行傅里叶变换,把空间域满足的二维积分问题转化为不同波数相互独立的一维积分问题,并行性高;垂向一维积分采用基于二次插值的形函数积分实现,将z方向离散成M个单元,每个单元积分均可得到解析表达式,计算精度高;垂向保持空间域,便于浅层网格适当加密,深层网格适当稀疏,兼顾计算精度、计算效率及模拟复杂地形的需求。
1.2 磁场和磁梯度张量
根据空间域磁场、磁梯度张量与磁位的关系
(5)
式中,B为空间域磁感应强度。
(6)
式中,T为空间域磁梯度张量。由式(5)得空间波数混合域磁位与磁场关系
(7)
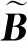
(8)

1.3 形函数一维积分
垂向空间域一维积分,将一维积分沿深度方向剖分成M个单元,在每个单元内磁化强度满足二次变化,笔者采用二次插值的形函数进行积分,在磁场变化快的地方加密网格,磁场变化慢的地方剖分稀疏,既能保证计算精度,又能减少计算量。
对空间-波数混合域磁位积分公式(2)离散
(9)
sign (k))e-|k||z-z'|dz'
(10)
sign (z-z'))e-|k||z-z'|dz'
(11)
式中:zj、zm分别为单元积分的下限和上限。
将磁化强度表示成单元节点磁化强度的二次形函数
(12)
(13)
将式(12)~式(13)代入式(10)~式(11)中,整理可得
(14)
(15)
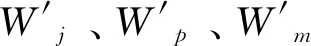
1.4 起伏地形条件下的快速算法
对于起伏地形条件下的二度体磁异常数值模拟,将地下研究区域海拔最低点与最高点之间剖分为n个深度节点(起伏地形模型见图1)。常规算法需要计算海拔最高点与最低点之间n个深度节点所在水平测线的磁异常,然后通过插值求得起伏地形上的磁异常,计算量是水平地形条件下的n倍,计算量大,效率低。针对这一问题,笔者提出一种针对起伏地形条件下二度体磁异常数值模拟的快速算法。
以x分量积分为例,形函数单元积分公式为
e-|k||zp-z'|dz'
(16)
其中,zp为起伏地形上不同深度的节点。
垂向一维积分Ix(k,zp)积分区域由三部分组成(图1所示中的(1)、(2)、(3)),故式(16)可以表示为
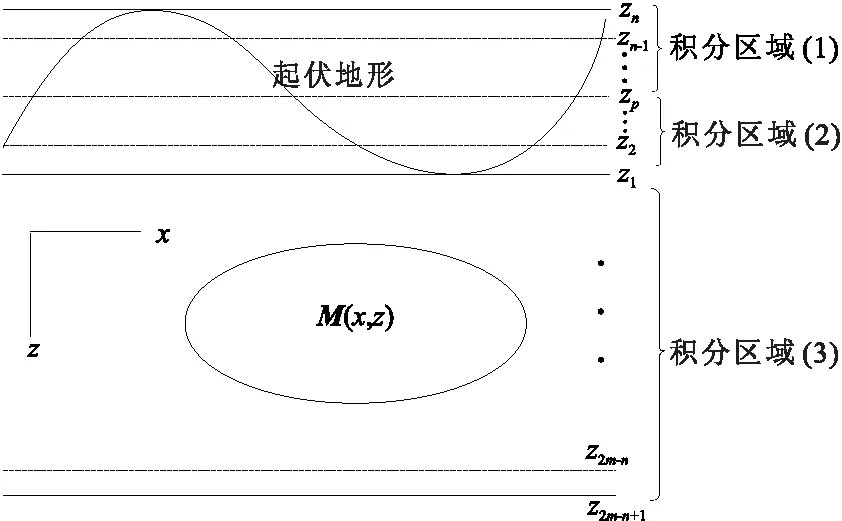
图1 地形起伏模型示意图Fig.1 Topographical model
Ix(k,zp)=Ix1(k,zp)e-|k|zp+Ix2(k,zp)e|k|zp+
Ix3(k,zp)e|k|zp
(17)
其中
(18)
其中:m1、m2、m3分别为三部分积分区域的单元个数。
由式(16)可知,①计算不同深度节点zp所在测线磁异常时,Ix3(k,zp)是相同的,即对于不同的深度节点zp,地形最低点以下的积分只需计算一次;②随着深度节点zp从地形最低点z1向上移动,深度节点zp的积分Ix1(k,zp)、Ix2(k,zp)与深度节点zp-1的积分Ix1(k,zp-1)、Ix2(k,zp-1)存在积分区域重叠,重叠区域可只计算一次;③当计算深度节点z1时,积分区域变为Ix2(k,z1)和Ix3(k,z1),当计算深度节点zn时,积分区域变为Ix1(k,zn)和Ix3(k,zn)两部分。
根据式(16)积分特点,当计算深度节点zp所在测线磁异常场时,可利用上一个深度节点zp-1的积分计算结果,避免了重复计算,提高了计算效率。快速算法主要流程如下:
1)计算起伏面最低点z1节点所在线磁异常场。由式(18)计算z1节点上下两部分积分Ix2(k,z1)、Ix3(k,z1),并对Ix3(k,z1)及Ix2(k,z1)每个单元积分结果进行存储。
2)计算下一个深度节点z2。由积分公式特点可知,z2节点的Ix3(k,z2)与z1节点的Ix3(k,z1)相同,可直接调用已存储结果;z2节点的Ix2(k,z2)积分区域包含在z1节点Ix2(k,z1)积分区域以内,每个单元计算结果已经计算存储,可直接调用;计算Ix1(k,z2)并存储。
3)其他深度节点依次类推,直到计算出最高点zn节点所在平面磁异常场,然后通过插值得到起伏地形上磁异常场。
2 模型算例
在模型算例中,首先设计突变介质模型用于验证本文算法的正确性和可靠性,即采用基于4个高斯点的高斯FFT,计算了空间-波数混合域二度体磁场及其梯度异常,并与空间域解析解[15]对比,验证本文算法的正确性和可靠性。其次通过对比复杂地形条件下的磁异常场快速算法与常规算法的计算时间与计算精度,验证基于形函数积分快速算法的有效性和高效性,并分析了地形起伏最低点与最高点之间垂向剖分节点个数对磁异常场计算精度的影响规律。最后设计非规则复杂模型用于研究不同观测高度的磁场分量响应特征。
2.1 正确性验证
设计如图2所示的异常体模型。模拟区域大小为1 000 m×500 m,网格剖分为201×101,水平和垂向网格间距均为5 m;异常体模型位于研究区域中心位置,异常体宽为400 m,厚度为100 m,顶面埋深为200 m,底面埋深为300 m,异常体的磁化率为 0.01,地球正常磁场强度为45 000 nT,磁倾角为45°,磁偏角为0°。
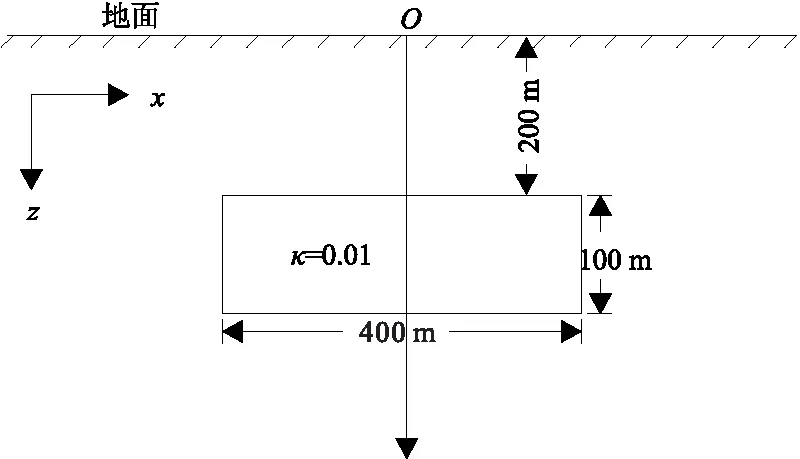
图2 异常体模型示意图Fig.1 Anomalous body model
图3为磁位和磁场的解析解、数值解以及地面z=0各节点的相对误差。从图3中可以看出:磁位和磁场的数值解与解析解吻合较好,地面节点磁位的最大相对误差为0.48%,地面节点磁场Bx分量和Bz分量最大相对误差均为0.52%。图4为磁梯度张量的解析解和数值解,以及地面节点的相对误差。从图4可以看出,磁梯度张量的数值解与解析解吻合较好,地面节点磁梯度张量的最大相对误差为0.22%。综合图3和图4可以得出如下结论:磁位、磁场和磁梯度张量的数值解和解析解对相对误差均很小,仅在模型突变点附近误差略有增大,故验证了本文算法的正确性,且计算结果表明其精度较高。
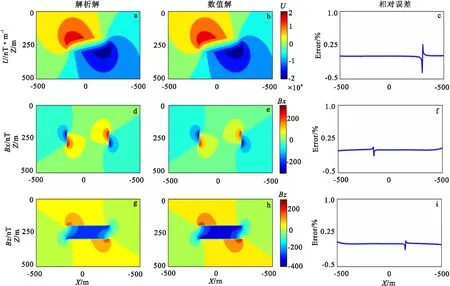
图3 磁位、磁场数值解、解析解及地面节点相对误差Fig.3 Numerical and analytical solutions of magnetic potential, fields and relative errors of ground nodes(a)磁位U解析解;(b)磁位U数值解;(c)磁位U相对误差;(d)Bx解析解;(e)Bx数值解; (f)Bx相对误差;(g)Bz解析解;(h)Bz数值解;(i)Bz相对误差
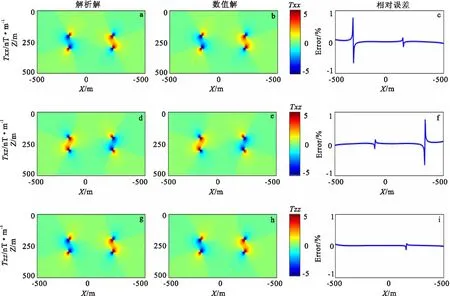
图4 磁梯度张量数值解、解析解及地面节点相对误差Fig.4 Numerical and analytical solutions of magnetic gradient tensor and relative errors of ground nodes(a)Txx解析解;(b)Txx数值解;(c)Txx相对误差;(d)Txz解析解;(e)Txz数值解; (f)Txz相对误差;(g)Tzz解析解;(h)Tzz数值解;(i)Tzz相对误差
2.2 计算精度与计算效率
设计如图5所示起伏地形组合模型,验证本文提出的快速算法对复杂地形的适应性。地形起伏用式(19)所示的函数描述,模拟区域地形起伏最低点与最高点之间高差为2 km。
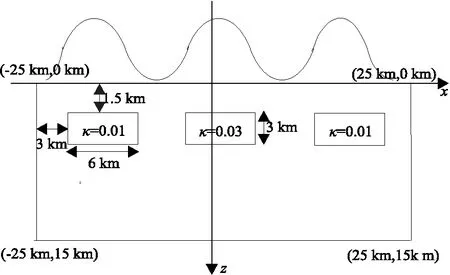
图5 组合模型地形起伏示意图Fig.5 Combined model with topography
x∈[-25000,25000]
(19)
起伏地形最低点以下计算区域为50 km×15 km,网格剖分为1001×501,水平网格间距为50 m,垂向网格间距为30 m,起伏地形最低点与最高点之间垂向剖分11、21、31、41、51节点。在计算区域分布着三个大小相同的异常体,异常体宽为6 km,厚度为3 km,顶面埋深距地形起伏最低点为1.5 km。左右两个异常体的磁化率均为 0.01,中间异常体的磁化率为0.03;地球正常场的磁化强度为45 000 nT,磁偏角为0°,磁倾角为45°。
针对该模型,分析对比了起伏地形最低点与最高点之间垂向剖分节点个数对快速算法与常规算法计算效率和计算精度的影响,计算效率和计算精度统计结果如图6所示。本文算法均采用fortran 95语言编写,模型算例均在配置为CPU-Inter Core i5,主频3.30 GHz,物理内存32.00 GB的台式机上串行测试得到。
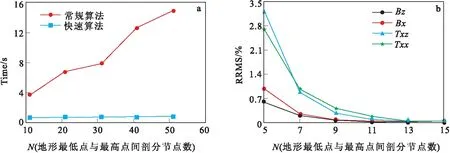
图6 快速算法的计算精度与计算效率图Fig.6 Calculation accuracy and efficiency of the fast algorithm(a) 计算效率;(b)计算精度
从图6(a)可以看出常规算法的计算时间随着N(起伏地形最低点与最高点之间剖分节点数)的增大近似线性增长,快速算法的计算时间随着N的增大时间几乎不变;快速算法计算起伏地形最低点与最高点深度方向剖分11个节点的磁异常时间为0.72 s,约为常规算法的1/5;剖分51个节点的磁异常时间为0.88 s,约为常规算法的1/17;随着深度方向网格剖分节点个数N的增大,快速算法效率优势表现更为明显。
图6(b)为起伏地形上磁异常场及磁梯度张量相对均方根误差[14](rrms)随起伏地形最低点与最高点之间垂向剖分节点个数变化的规律[14]。从图6(b)中可以看出:起伏地形上磁异常场及磁梯度张量的计算精度随着剖分节点个数的增加而提高。起伏地形最低点与最高点之间剖分9个节点时,磁异常场及磁梯度张量的相对均方根误差小于0.5%。当剖分节点个数大于9时,磁异常场及梯度张量的相对均方根误差几乎不再变化。
为了兼顾计算精度与计算效率,图7给出了起伏地形条件下最低点与最高点之间剖分15个节点的起伏地形上磁场和磁梯度张量数值解与解析解。由图7可知:磁场与磁梯度张量不同分量的解析解与本文算法结果基本重合,地面磁异常场的最大相对误差为0.50%,地面磁梯度张量的最大相对误差为0.15%,表明本文提出的起伏地形条件下磁异常快速算法精度高,速度快,适用性强。
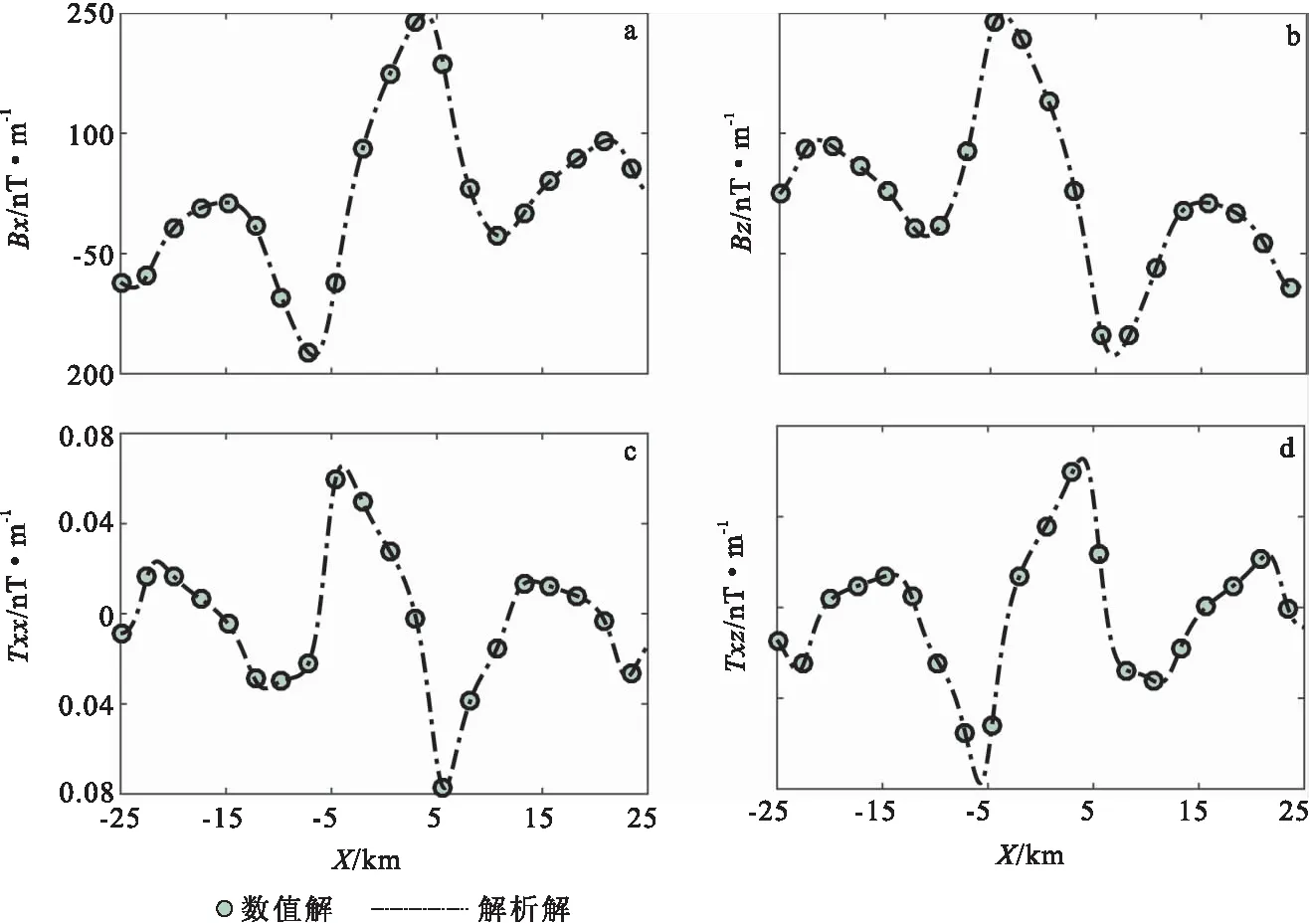
图7 起伏地形上磁场、磁梯度张量数值解与解析解Fig.7 Numerical and analytical solutions of magnetic fields and gradient tensor on undulating terrai(a)Bx;(b)Bz;(c)Txx;(d)Txz
2.3 复杂模型
为了进一步检验本文算法对非规则复杂二度体磁异常计算的有效性,设计了如图8所示的复杂地形模型。研究区域范围均为:x方向从-200 m到200 m,z方向从-200 m到200 m。z轴铅垂向上为正,网格剖分大小为401×201。图8起伏地形异常体部分由山谷和山脊构成。非规则异常体的磁化率κ为0.02,背景介质的磁化率为“0”,地球磁场强度为45 000 nT,磁倾角为45°,磁偏角为0°。 这里分别在起伏地形和观测面为40 m和100 m的高度上观测,计算结果如图9所示。从图9中可以看出,在起伏地形上观测的磁异常分量在地形突变点处有明显的异常拐点,在山脊上存在明显的正异常响应,山谷处存在明显的负异常响应,且Bz分量的最大异常幅度明显大于Bx分量最大异常幅度;随着观测高度的增加,磁异常场响应逐渐变缓;山脊磁异常体正上方磁场Bx分量的正异常幅值较大,Bz分量的负异常幅值较大,山谷磁异常体正上方Bx和Bz分量的正负异常幅值均相对较小,且比较平滑,这是由于左边山脊磁异常体的体积明显大于右边山谷磁异常体。通过研究非规则复杂模型起伏地形上和不同观测高度的磁异常响应特征,为磁异常反演成像和地质解释提供借鉴。
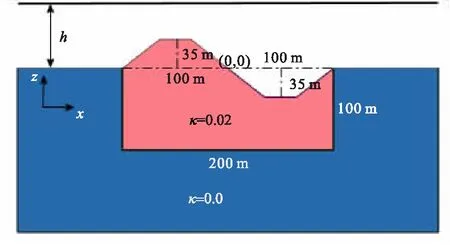
图8 复杂地形模型Fig.8 The complex topographic model

图9 不同高度磁场分量Fig.9 Results of magnetic field components at different heights(a)Bx;(b)Bz
3 结论
这里提出一种基于积分解的空间-波数混合域二度体磁异常数值模拟方法。该方法充分利用傅里叶变换方法和形函数积分的特点,将一个二维积分问题转化为一维准解析积分问题,有效提升了计算效率。数值试验结果表明:该算法数值精度高、计算速度快、适应性强,尤其适用于任意起伏地形条件下的磁异常及其梯度场的高效、高精度模拟,为二度体或三度体位场高效数值模拟提供了一种新的研究思路。
