基于改进ORB和RANSAC算法的无人机影像特征匹配方法

丁进选，王丽欣，苗星雷

(1.深圳市长勘勘察设计有限公司，广东 深圳 518003；2.黑龙江省测绘地理信息学会，黑龙江 哈尔滨 150080；3.哈尔滨北方防务装备股份有限公司，黑龙江 哈尔滨 150050)

无人机航摄具有机动灵活、高效快速和作业成本低等优点，在各领域得到广泛的应用[1-2]。由于在一些应用中通常需要覆盖整个研究区域的影像，因此需要对无人机获得的影像进行拼接。影像特征匹配作为其中一项关键环节[3-4]，得到众多研究者的关注。David Lowe等于1999年提出了著名的SIFT算法，并于2004年进行了改进[5]。Leutenegger等为解决SIFT算法实时性的问题，于2011年提出了BRISK算法[6]。Pablo等人于2012年提出了KAZE算法，但该算法对仿射畸变不耐受[7-8]。Rublee等人于2011年提出了一种对图像的平移、旋转、缩放等矩阵变换具有不变性的ORB算法，该算法具有计算速度快、占用内存小等特点[9]，但是该算法尺度性较差。部分学者从不同角度对ORB算法进行了改进[10-11]，但是均未有效解决ORB算法尺度性弱的问题。

本文在总结和分析ORB算法优缺点的基础上， 提出一种改进的无人机影像匹配算法。该算法首先利用改进的ORB算法提取具有尺度不变特性的特征点，并在特征匹配阶段基于改进的RANSAC算法进行误匹配的剔除，最终实现无人机影像特征的精确匹配。

1 ORB算法的改进

传统ORB算法分为特征点的检测和描述两部分，该算法具有对平移、光照和旋转不变的特性[9]，但是由于该算法未给描述子提供尺度信息，因此该算法不具备尺度不变性[12]。因此当影像尺度发生较大变形时，该算法性能表现较差。在ORB算法中，通常采用Harris角点函数对探测出的特征点进行排序，传统的Harris角点函数不具备尺度信息。

因此本文针对上述问题通过对Harris角点函数改进以使检测出的特征点具有尺度信息。

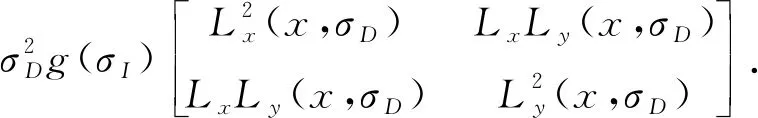
(1)

式中：σD是抵消缩放的微分尺度；σI是抑制噪声的高斯函数，此处σI=SσD，S为经验值，通常取0.7，其构造尺度空间的角点函数为：

cornerness=det(μ(x,σI,σD))-atrace2(μ(x,σI,σD)).

(2)

用LoG函数进行尺度检测，则：

(3)

式中：σn代表特征点尺度函数。对函数进行检测之后即可得到具有尺度信息的特征点。

2 RANSAC算法的改进

RANSAC作为一种经典的特征点对误匹配剔除算法，其首先采用无差别的方式在所有的特征点中进行随机采样，然后通过式(4)计算两幅图像之间单应矩阵的转换参数。

(4)

式中：(x,y)和(x′,y′)为待匹配点对坐标，其中a0…a7表示两幅图像之间的平移、旋转和缩放[13]。研究发现，粗匹配得到的部分特征点对存在较大的误差，在经典RANSAC算法中此部分点仍会被带入单应矩阵，这些误匹配导致RANSAC算法计算速度减慢，计算效率降低。当特征点数目较多时，上述缺陷变得尤为严重。因此本文引入空间一致性算法[14]的思想对RANSANC算法进行改进，通过空间一致性算法剔除误匹配点、缩小抽样点集样本数，减少迭代次数。

空间一致性理论基本思想：如图1所示为两面相似的窗户，若在每面窗户上分别检测出如图1所示的12个特征点，对于左侧窗户中圆中心的红色特征点，虽然其与右侧窗户中相同位置点的特征相同，但是考虑到其8邻域特征点的信息，则可知这两个特征点并不匹配，此即空间一致性理论的基本思想。

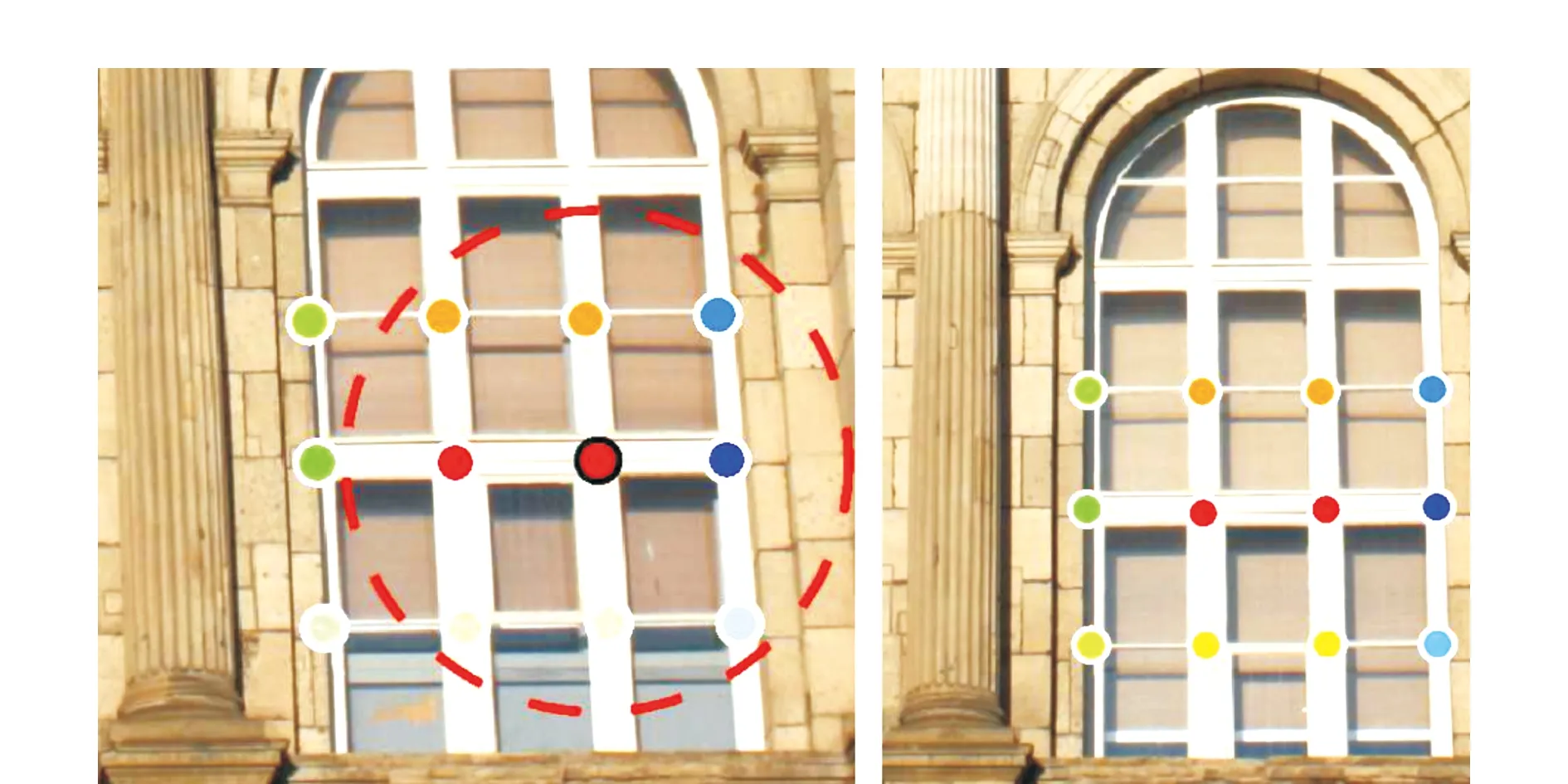
图1 空间一致性理论基本思想

空间一致性理论基本原理：对于任一影像Ii，定义其对应的尺度不变函数为:

NIi={(xj,yj,σj,dj)}.

(5)

式中：(xj,yj)是特征点中心对应的坐标；σj是图像的尺度；dj是特征点对应的描述子。

若将任一特征fi的邻域集合定义为NGi(fi)，则该集合包含以(xj,yj)为圆心，rσj为半径的圆内的特征点，尺度范围为(sminσj,smaxσj)。

NIi(fj)={fk∈f(Ii){fj}|‖(xk-xj,

(6)

式中:∧为取小运算。

设有一图像对(I1,I2)，定义该图像对特征点构成的匹配点集为C，则可得：

C={(f1,f2)|f1∈f(I1)∧f2∈f(I2)}.

(7)

N(c)={(f1,f2)∈C|f1∈

(8)

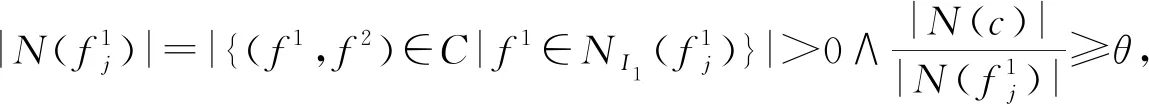
3 改进算法实验与结果分析

3.1 实验方案

为验证本文提出改进算法的普适性，本实验选用了两组具有代表性的无人机影像对，一组为城区包含建筑、道路和植被的影像对(研究区1)，另外一组为郊区包含灌木、草地和裸土的影像对(研究区2)，影像分辨率为640像素×426像素。分别采用本文改进算法和ORB+RANSAC算法对同一影像对进行特征点提取和匹配试验，并从提取特征点个数、特征匹配用时、最终总匹配数等角度进行对比分析。本试验的运行环境为：ThinkPad笔记本，处理器i5，CPU2.5 GHz，内存8 G，Windows7 64位操作系统。

3.2 实验结果与分析

3.2.1 实验结果

为验证本文提出算法的性能，首先对本文提出的改进算法和原算法(ORB+RANSAC算法)的特征点检测性能进行实验，然后进行匹配实验，两组影像对特征点检测结果见图2和图3；基于改进算法的粗匹配和精匹配结果见图4和图5；特征点对个数和匹配等信息见表1；改进算法尺度不变性实验结果如图6所示。

图2 研究区1特征点检测结果

图3 研究区2特征点检测结果

图4 基于改进算法的粗匹配结果

图5 基于改进算法的精匹配结果

表1 算法性能比较

3.2.2 结果分析

通过图2和图3可知，对于本研究选取的城区影像对(即研究区域1)和郊区影像对(即研究区域2)，改进算法提取的特征点个数均有所增加；实验结果表明，对于城区影像对右侧的影像，原算法检测出特征点500个，本文提出的改进算法检测出特征点507个；对于郊区影像对右侧的图像，原算法检测出特征点490个，本文提出的改进算法检测出特征点538个。

通过图4可知，对于本文提出的改进算法，在实验所用的两组影像对上进行粗匹配时仍存留一定的误匹配。

表1的研究数据显示本文所提出的改进算法在匹配精度上均有明显提升。如对于城区影像对匹配精度由24.12%上升到38.20%，提高了14.08%；对于郊区影像对匹配精度由41.55%上升到61.06%，提高了19.51%，印证了本文改进算法在剔除误匹配方面的有效性。

在匹配总用时方面，对于城区影像对，本文所提出的改进算法与原算法相比缩短了521 ms，效率提升约16%；而对于郊区影像对，本文算法用时比原算法减少559 ms，效率提升约19%。

通过图6可知，本文提出的改进算法能够有效克服影像尺度变化带来的影响；对于研究区2当影像尺度缩放为原尺寸80%时，改进算法识别出内点59对，匹配精度为39.07%；当影像尺度缩放为原尺寸70%时，改进算法识别出内点33对，匹配精度为25.38%；随着尺度变化的增大，改进算法匹配性能呈下降趋势。

4 结束语

本文对ORB算法和RANSAC算法进行了研究，结合前人的研究对Harris角点函数进行了改进，并将空间一致性理论应用到了RANSAC算法中，并选取两组具有代表性的无人机影像进行实验。实验结果表明，本文设计的改进算法，在特征点识别、误匹配剔除和尺度不变性方面的性能均有明显的提升，表明本文提出的改进算法在无人机影像配准方面的有效性，对解决影像配准具有一定的借鉴作用。