基于NSGA-Ⅱ算法的飞行器质心平衡供油策略研究
2021-07-13吴宗庆齐光宇通讯作者席伟伟
吴宗庆,齐光宇,沙 杰(通讯作者),席伟伟
(河南工业大学机电工程学院 河南 郑州 450001)
1 引言
在某类飞行器中,燃油作为重要的源泉,其通过6个油箱的联合供给以满足飞行器发动机在空中持续地工作,使其完成飞行任务需求。飞行器在飞行过程中,由于油箱内燃油的消耗使飞行的质心发生了变化,质心的变化会对飞行器在空中的控制产生微妙的变化,是飞行器控制的重要指标[1]。因此,制定油箱的供给策略对于这类飞行器来说是一项重要任务。
2 飞行器质心平衡策略分析
飞行器在空中飞行时,6个油箱的状态会随着飞行姿态发生改变,油箱内的液体平面的法向始终相对地心引力方向平行[2-3]。为了求解每个时态的质心点位移变化,将这些指点分解为若干个三角形,即求解出这些三角形的质心向量,最终对这些向量进行求和即为所求总质心变化动态[4]。实际质心位置与给出的理想位置的欧式距离最大值和最小值,则采用NSGA-Ⅱ算法进行最优解求解。
3 模型的建立与求解
根据文献知燃料的密度为850 kg/m3,飞行器净重2800 kg,结合6个油箱的基本尺寸,油箱质心及坐标位置,并要求结合所给的飞行器供油曲线及飞行器的仰角,得出质心的变化曲线。通过多组讨论的形式,即将多边形分割为多个三角形,通过计算每个三角形的质心得出多边形的总质心[5]。求区域质心:封闭区域为D,密度公式为F(x,y),求质心公式为:,由以上式子表述其质心的x,y,z坐标为:
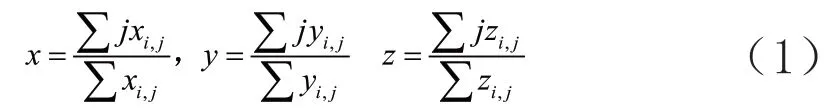
平面多边形被剖分为i个简单图形x1,x2,x3...xi,每个?简单图形的质心点为xi,j,j为相对应的向量。那么这个平面多边形的质心点x轴坐标为x,同理y,z质心位置。这里多边形就可被分割为多个三角形,利用向量求出相对应的质心坐标。在问题中由于存在着俯仰角,这会使原本的与O-xy相平行的水平油面发生侧移,组成新的形状,如五边形,与梯形的状况.可根据俯仰角的变化形成的液体体积图形,求出各个的质心向量,之后进行累加向量之和得出相应的质心变化,即为总的质心变化结果。
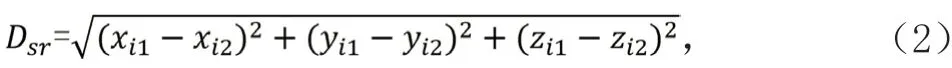
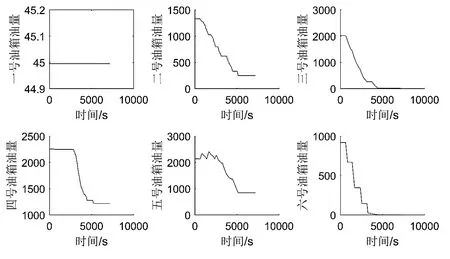
图1 6个油箱供油图
4 结论
将每个时态的质心点位移分解为若干个三角形,多边形的总质心由每个三角形的质心得出相加得出。简化了模型计算的复杂程度,提高了模型的可行性。可以使需要优化的变量向全局最优逼近,在建造供油策略最优解模型,使用NSGA-Ⅱ算法,使得供油求解结果更优于遗传算法,将结果的精度往前推进,模型在求最优解时,没有将整体通过智能优化算法进行整体求解,而是采用了分步优化,不仅使得模型的扩展性和可移植性增强,也大大提高了模型的精度。
