行波效应作用下自锚式悬索桥地震响应分析
2021-07-13谭伟,余振
谭 伟,余 振
(1.中国市政工程西南设计研究总院有限公司,四川 成都610081;2.中都工程设计有限公司,四川 成都610041)
0 引言
近年来,悬索桥因为跨越能力强、外观优美等特点,在桥梁建设中被广泛应用。地震动空间性,特别是行波效应可能对大跨度悬索桥的地震响应造成低估或高估,需要专门进行抗震研究。因此,行波效应对悬索桥抗震分析结构有重要影响,需要特别重视。其主要原因在于,桥梁的跨度相对于震源到桥址的距离不能忽略,地震波到达各桥塔存在时间差,从而会激励起大跨度悬索桥对称和非对称振型参与,从而激起比一致激励更多的振型参与。因此,考虑行波效应对大跨度悬索桥结构抗震性能的影响十分必要[1-2]。
目前已有不少学者[3-7]研究了行波效应地震动空间性对悬索桥地震响应的影响。雷虎军等[8]研究了高速铁路悬索桥在行波效应下的行车安全性,发现不考虑地震行波效应会严重低估列车的行车安全指标。黄康等[9]研究了大跨度悬索桥的行波效应。结果表明,梁端响应对视波速的大小较敏感。易富等[10]采用大质量法,基于人工地震波分析了大跨度悬索桥的多点激励地震响应,发现桥梁结构受行波效应影响较大,大跨度桥梁抗震中应重视。
本文针对某自锚式悬索桥,利用有限元软件SAP2000建立了三维有限元模型,并基于合成的人工地震波进行非线性动力时程分析,研究了行波效应对大跨度悬索桥动力响应的影响,研究结论可为大跨度悬索桥抗震设计提供参考。
1 人工地震波合成介绍
悬索桥所在场地的地震特征对桥梁地震响应有重要影响。本文根据悬索桥所在场地的特征,通过《建筑抗震设计规范》得到设计反应谱,如图1所示。再由设计反应谱通过迭代法得到功率谱,并求得傅里叶幅值谱。最后,根据傅里叶逆变换得到加速度时程曲线。
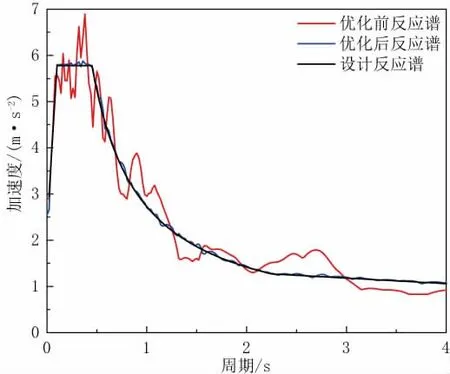
图1 反应谱比较
本文假设单质点体系响应yp,s的方差为σy(t),在持续的时间段t(30 s)内,不超过概率为p的最大反应yp,s可表示为[11]:

式中:rp,s为峰值系数。
首先,根据Vanmarcke方法[12-13],可知设计加速度反应谱Sa(ωj,ξ)和对应的功率谱G(ωj)之间的近似换算关系为:
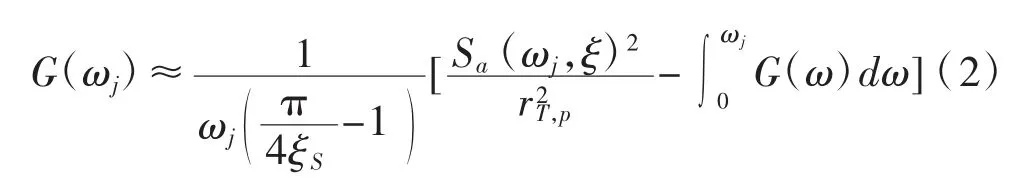
根据式(2)可得到功率谱函数。接着将求得的功率谱进行傅里叶变化,可得到如图2所示的加速度时程曲线,其反应谱如图1所示。从图1可以看出,人工合成的加速度时程曲线对应的反应谱和设计反应谱之间存在较大的误差。这是因为设计反应谱到功率谱的转换公式是近似公式,存在不可避免的误差。
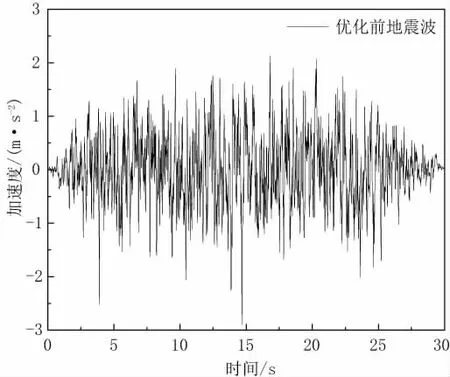
图2 优化前的加速度时程曲线
为提高人工合成的加速度反应谱和设计反应谱的拟合程度,可以使用小波函数方法[14]进行优化。从图1可以看出,优化后的时程加速度曲线对应的反应谱形状接近设计反应谱,比优化前的反应谱拟合程度更高。因此,优化过后的加速度时程曲线(图3)更能体现悬索桥所在场地的特征,其计算结果更可靠。

图3 优化后的加速度时程曲线
2 大质量法的基本原理
本文使用大质量法来考虑行波效应对桥梁结构地震响应的影响。大质量法的基本思想是:先在结构的每个约束点上分别施加一个无限大质量的质量点(一般取结构质量的103~106倍),并释放结构约束点处在地面运动方向上的约束。在SAP2000中进行行波效应分析时,只需将优化后的加速度时程曲线定义为新的载荷工况,然后根据地震波的传播速度(本文中视波速取值1 000 m/s2)和桥梁各支撑点之间的距离,计算出地震波到达个支撑点时的时间间隔,从而达到考虑行波效应的目的。
3 三维有限元模型
本文以某大跨度自锚式悬索桥为研究对象,在有限元分析软件SAP2000的CSIBridge模块建立有限元模型。该悬索桥采用三跨结构,三跨的跨度分别为751 m,1 560 m和600 m。主梁采用箱梁结构,中跨设置吊杆。2个塔桥高均为250 m,其中墩高为50 m,如图4所示。
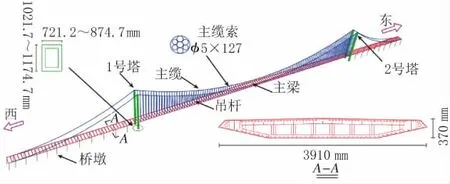
图4 悬索桥有限元模型
4 结果分析
为全面分析行波效应对该悬索桥的地震响应影响,本节比较了考虑行波效应的结构地震响应和未考虑行波效应(一致激励)的结构地震响应。图5和图6分别给出了在顺桥向地震下,1号和2号桥塔塔底剪力在不同视波速下的变化情况。当视波速在400~1 200 m/s时,1号桥塔的塔底剪力随着视波速的增加而增加;当视波速达到1 200 m/s时,剪力响应的最大值是一致激励的1.06倍。当视波速大于1 200 m/s时,剪力随着视波速的增加而减小。2号塔塔底最大剪力随着视波速的增加而增加,并在视波速达到1 600 m/s时,剪力达到最大,为一致激励的1.05倍。

图5 1号桥塔塔底剪力比
图6 和图7分别为1号和2号桥塔塔底弯矩在不同视波速下的变化规律。从图7可以看出,随着视波速的增加,桥塔塔底弯矩在一致激励的剪力值附近上下波动,没有明显的响应规律。弯矩最小时是一致激励的0.90倍,最大时是一致激励的1.19倍。图8的结果表明,考虑行波效应的情况下,2号塔塔底弯矩的大小总是小于一致激励的工况,在视波速为1 200 m/s时,塔底弯矩有最小值,为一致激励的0.71倍。在视波速为800 m/s时有最大值,为一致激励的0.93倍。
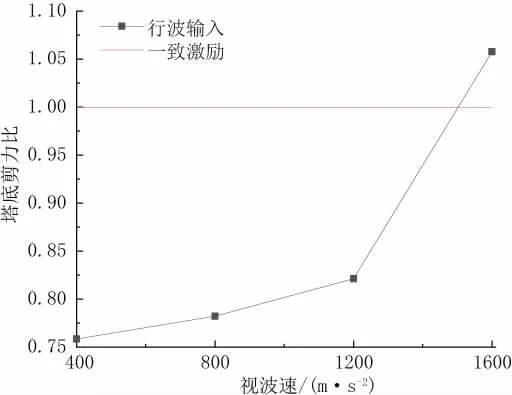
图6 2号桥塔塔底剪力比
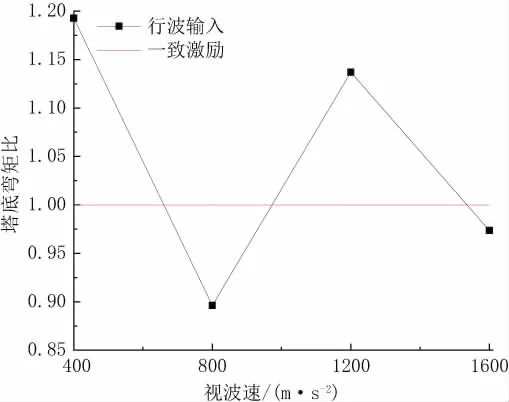
图7 1号桥塔塔底弯矩比

图8 2号桥塔塔底弯矩比
图9 和图10展示了悬索桥1号塔和2号塔塔顶的顺桥向位移。从中可以看出1号塔塔顶位移随着视波速的增加而减小,2号塔塔顶处位移随着视波速的增加而上下振荡。总体上看,行波效应对桥塔塔顶的位移响应影响很大,考虑行波效应的最大位移约为一致激励的2倍,这一数值远超上文中内力分析时的数据。因此在悬索桥设计时,需要提高桥塔的刚度来应对行波效应对桥塔的影响。
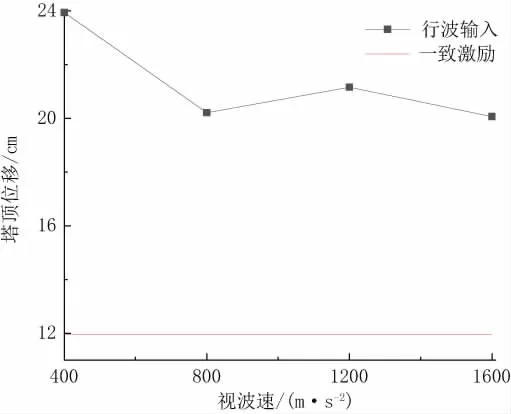
图9 1号桥塔顶部顺桥向位移
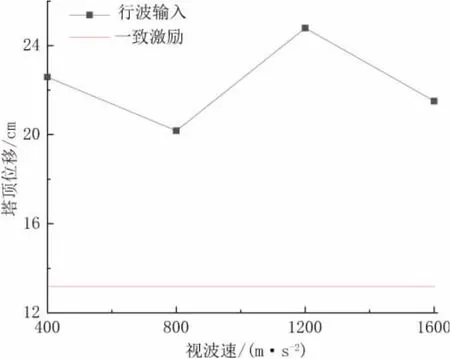
图10 2号桥塔顶部顺桥向位移
图11 ~图13展示了考虑行波效应的情况下,桥塔桥底剪力、弯矩和桥顶位移的最不利响应。图11对应到图5视波速为1 200 m/s的行波输入点,其最大值为5.21×106N。图12展示了2号塔在视波速为400 m/s的地震激励下塔底的弯矩响应曲线,其最大值为6.21×108N·m。图13对应到图10中塔顶位移的最大点,其视波速为1 200 m/s。三张图具体地展示了不同视波速下最不利响应的曲线细节,表明了不同视波速下内力响应和位移响应的最大值并不相同。因此,考虑大跨度悬索桥的行波效应十分必要。
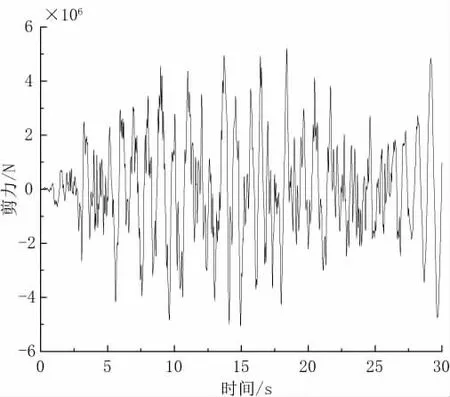
图11 1号桥塔塔底剪力(视波速1 200 m/s)
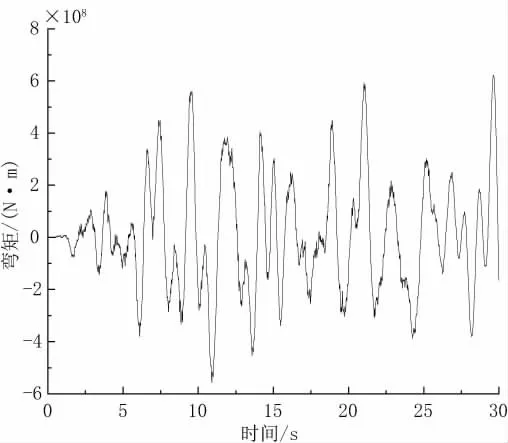
图12 1号桥塔塔底弯矩(视波速400 m/s)
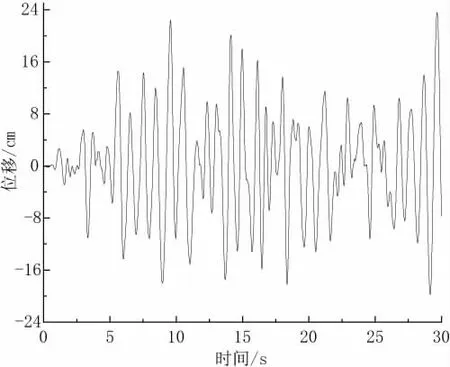
图13 2号桥塔顶部顺桥向位移(视波速1 200 m/s)
5 结 论
本文使用设计反应谱生成人工地震波,并用小波函数方法对地震波进行优化,得到更接近设计反应谱的优化地震波。再用大质量法分析视波速为400 m/s、800 m/s、1 200 m/s和1 600 m/s时的行波效应对悬索桥结构响应的影响,并将结果和一致激励的情况进行比较。得到的结论如下:
(1)行波效应对悬索桥桥塔塔底剪力的影响规律不相同。波速小于1 200 m/s时,桥塔塔底剪力随着视波速的增加而增加。视波速大于1 200 m/s时,1号塔塔底剪力随着视波速的增加而减小,2号塔塔底的剪力则在增加。
(2)考虑行波效应时,桥塔塔底的弯矩随着视波速的增加而上下波动,但1号塔塔底弯矩大小在一致激励处上下波动,2号塔塔底弯矩响应一直小于一致激励。
(3)桥塔塔顶位移受行波效应的影响较大,桥塔塔顶最大位移响应是一致激励的2倍。因此,在进行大跨悬索桥设计时,需要充分考虑行波效应对桥塔塔顶的影响。
