辛算法的分类与发展

孙 浪，刘福窑，王 颖，孙 威,3

(1.上海工程技术大学 数理与统计学院，上海201620；2.上海工程技术大学 计算物理与应用研究中心，上海201620；3.安庆师范大学 资源环境学院，安庆246133)

1 引言

哈密顿系统从物理本质上具有辛结构的不变性。20世纪80年代初期，中国学者冯康先生[1]与Ruth[2]几乎同时提出能够保持哈密顿相流辛结构的数值积分算法，解决了传统算法因长期对时间积分不能保持系统的能量守恒的问题[4]。前者主要对不可分的哈密顿系统采用以隐式中点法为基础来构建高阶隐式辛算法，后者主要是针对可分解为动能T和势能V的哈密顿系统建立显式辛算法。显式辛算法和隐式辛算法的区别在于积分过程中是否需要迭代计算。

在Ruth建立的T+V形式的显式辛算法的基础上，高阶辛算法的研究和应用得到了快速发展[5]。当哈密顿分解成主要的未受摄部分H0和次要的摄动部分εH1且两部分均可积时[6]，可以通过升高摄动项εH1的小参数ε的阶提高精度，即类高阶辛算法(pseudo-highorder-symplectic integrator,PSI)[7]和辛校正(wisdom-holman-touma correction,WHT)[8]。力梯度辛算法[6]是在算法的Lie算子中嵌入了力梯度算子，可以有效避免负时间系数的出现。Ruth[2]和Chin[9,10]分别构造了三阶力梯度辛算法和四阶力梯度辛算法。李荣和伍歆[12–14]结合McLachlan[11]的算法优化思想构造了三阶优化力梯度辛算法和四阶优化力梯度辛算法。陈云龙和伍歆[15]论证了力梯度辛算法在求解旋转坐标系下的圆型限制性三体问题的有效性。

哈密顿系统变量不可分离时，显式辛算法一般不能直接应用，隐式辛算法应该适合应用。常用隐式辛算法有半隐式辛算法[16,17]和隐式中点法[16–23]。隐式辛算法适合任意哈密顿系统，但计算效率低，不宜作为首选数值方法。为使显式辛算法在不可分哈密顿系统中得到应用，Pihajoki[24]在不可分哈密顿系统中增加了一组与原相空间动量坐标相同的量，提出了相空间扩充对称算法，但系统的辛结构被破坏。Tao[25]在Pihajoki的基础上将哈密顿系统分成三部分，第三部分是两组坐标动量差的平方组成的约束哈密顿，保证了数值解在扩展相空间中的辛结构。在此基础上，Liu和Wu[26,27]构造了连续坐标动量置换相空间扩大法，算法适合求解后牛顿哈密顿问题和旋转哈密顿问题等哈密顿系统不可分的问题，但在旋转致密双星后牛顿哈密顿系统中不能保持系统的能量稳定。Luo等人[28,29]提出了中点置换相空间扩大方法，这种方法优越于Pihajoki方法和刘磊等人的方法，它对算法的算子个数没有要求，适用范围更广。Wu等人[30]提出的扩大相空间优化Forest-Ruth算法在平面圆型限制性三体问题和致密双星问题中与未优化算法相比精度得到了明显改善，且表明采用中点置换能使优化的Forest-Ruth算法具有更好的数值表现。Li和Wu[31]在Mikkola等人[32,33]的基础上结合扩大相空间中的几种置换方法，提出了扩大相空间的对数哈密顿显式对称法。这些方法在圆型限制性三体问题、三阶后牛顿自旋致密双星系统和Ernst-Schwarzschild黑洞等模型中表现出了高精度和高效率。辛算法在解决各类天文学物理模型中得到了较为广泛的应用。本文的主要目的是对上述辛算法及类辛算法的发展、构建以及适用物理模型进行阐述。

2 辛算法的建立

按照T+V分解形式，假设哈密顿可以表示为：

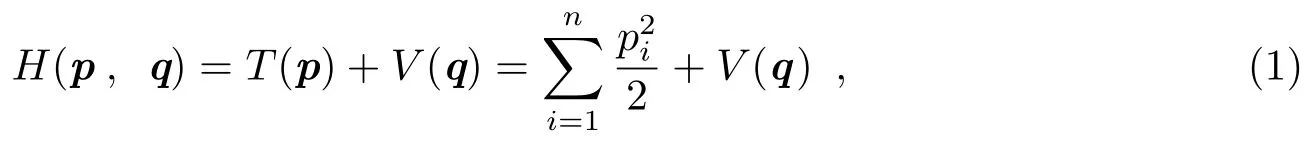
式中，p,q分别表示广义坐标和广义动量。相应的正则运动方程：

或取z=(p,q)

其中，L H是Lie算子，分别以A和B约定T和V的Lie导数：

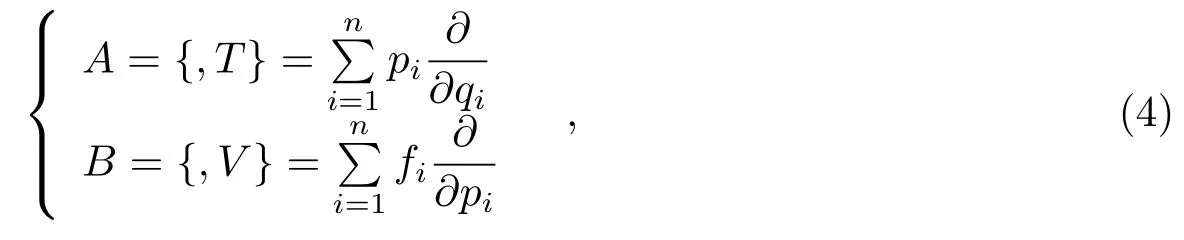
式中，τ为时间步长。设W={,H}，将W的指数幂可以用A和B的指数幂多次组合而成，即

a i和b i是由特定的阶确定的系数，O(h K+1)指哈密顿函数的K阶截断误差。若使Lie算子的个数等于阶条件的个数，时间系数可以很容易被算出。Ruth[2]在文献中提出了比较常用的二阶和三阶辛算法。在此基础上，Forest-Ruth四阶非力梯度辛算法[3]和Yoshida高阶非力梯度辛算法[5]也相继被建立。

3 非力梯度显式辛算法

3.1 T+V分解法

3.1.1 未优化的非力梯度显式辛算法

按照Ruth[2]的方法，对于可积分离的哈密顿系统，辛算法构造如下，

(1)一阶显式辛算法

(2)二阶显式对称辛算法

二阶显式对称辛算法由三个单指数算子构成，它的构造形式为：

(3)三阶显式辛算法

三阶显式辛算法由6个单指数算子构成，它的构造形式为S3：

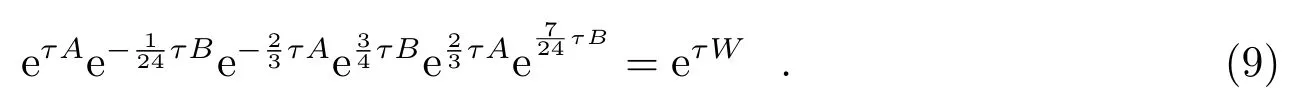
(4)四阶显式Forest-Ruth辛算法(fourth-order-Forest-Ruth symplectic integrator,FR)

Forest-Ruth算法从式(6)出发，它由7个单指数构成S4：

构造高阶算法的另一个思路是直接对二阶辛算法进行多重积，Yoshida[5]在Ruth[2]的理论基础上用三个二阶辛算法对称组合得到四阶显式Yoshida辛算法S YO：

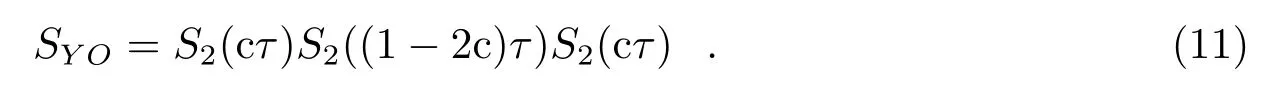
同年Forest和Ruth[3]提出了Forest-Ruth四阶辛算法，这两种辛算法构造可以达到等价的效果。按照上述算法构造方式，高阶辛算法S2n+2可以被构造[5]，

3.1.2 优化的非力梯度显式辛算法

McLachlan[11]1992年提出了算法的优化概念，通过将主要截断误差项的影响降到最小，得到优化系数，从而构造优化的二阶显式辛算法和三阶显式辛算法。在此基础上，四阶优化非力梯度算法[34]等高阶优化算法也被建立起来。

(1)二阶优化的显式辛算法和三阶优化显式辛算法

单一化系数表示的二阶显式辛算法的主要误差函数为：

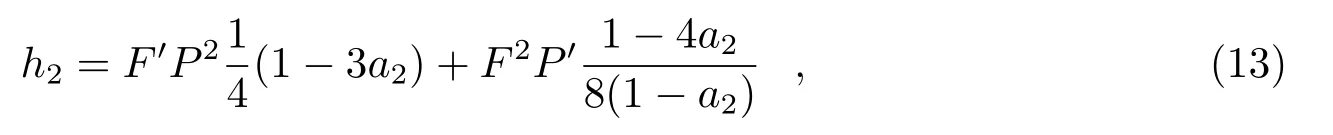
表1 几种显式辛算法的截断误差比较[11]

由此，McLachlan将n阶辛算法的主要误差函数表示为：

f j和g i表示误差常数。令该式的系数平方和最小，得到三阶最优化辛算法O3：

(2)四阶显式优化Forest-Ruth算法(fourth-order-optimal-Forest-Ruth integrator,OFR)Omelyan等人[34]将四阶显式Forest-Ruth算法拓展分解为：

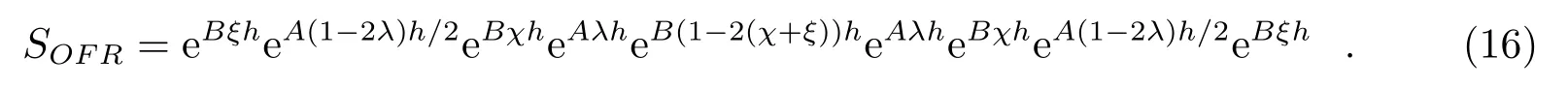
ξ,χ,λ为3个步长系数，它们之间存在两个约束条件，A的系数α(ξ,χ,λ)=0，B的系数β(ξ,χ,λ)=0。由于仍存在一个自由度，步长系数的取值将有多种解。从McLachlan的优化思想出发，令四阶显式Forest-Ruth算法的三阶截断误差为零及五阶截断误差项系数平方和最小，得到最优解：

该组合系数解下的OFR算法的截断误差值为γmin=0.000 92，四阶FR辛算法的截断误差值为γFR=0.039，优化后的精度得到了显著提高。

(3)优化的四阶类Suziki算法(fourth-order-pseudo-Suziki integrator,SU)

Omelyan等人[34]在Yoshida构建的四阶辛算法两端各加入两个相同算子构建了SU算法，它由5个算子组合而成：

考虑满足阶条件和截断误差h5系数平方和最小，得到的哈密顿截断误差值为γ=0.001 1，与OFR算法相比，误差精度低一个量级。

3.2 H=H0+εH1分解法

其中，H0和H1可积，H0是主要项，H1是摄动项，小参数ε表示H1与H0有量级ε的差别，具体分解过程在文献[35]中有详细描述。

规定A={,H0}和B={,H1}，由辛算法的构造公式eτW=eτAeτB[2]并反复利用Baker-Campbell-Hausdroff(BCH)公式[36,37]得到哈密顿函数的误差表达式：

a1,b1是误差项系数，从上式可以得到三种提高辛积分器的精度方法：(1)提高τ的幂次得到高阶辛算法；(2)改进哈密顿的分解方式和构造方式，ε越小，精度越高，比如哈密顿函数摄动分解[6]、时间变换以及扩展相空间；(3)升高ε的幂次，得到辛校正[8]。若误差项中的O(ε2τn+1)仍存在，升高τ的幂次得到类高阶辛方法[7]。这两种类辛算法不需要减小积分步长，也不用升高积分的阶就能优化积分精度和效率。一般情况下，哈密顿函数按照H=H0+εH1分解时，与T+V分解相比，算法精度有显著提高。如图1所示，以纯开普勒问题为例，摄动分解时的算法的数值精度比T+V分解提高了接近5个量级。

图1 纯开普勒问题在两种哈密顿分解形式中的能量误差

3.2.1 辛校正

Wisdom和Holman[6]在雅可比坐标系建立了如下的二阶辛算法(second-order-wisdomverlet,MV2)：

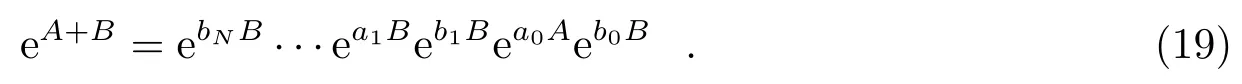
其中，N=1,b0=b1=1/2,a0=1。MV2的数值结果对应的哈密顿函数和真实哈密顿函数H的关系为=H+Herr。Wisdom等人[8]运用Lie级数算子构造一个正则变换的生成函数W，Herr不含摄动小参数ε的一或者二次幂项，从而构造辛校正公式。辛校正具有如下特点：(1)在不需要减少步长也不需要升高阶数的情况下，通过消去误差项中的ε或ε2项，实现一阶或者二阶辛校正来显著提高数值精度；(2)辛校正不严格保辛，但没有引入耗散机制；(3)计算效率高。

WHT计算生成函数W的过程较为繁琐，而且校正子C只适用于上述辛算法，不具备一般性。Mikkola和Palmer[39]借助Euler-Mclaurin式推导出辛校正的生成函数W。同年，Chambers和Murisun[7]建立了类高阶辛算法。Duncan等人[40,41]借助日心坐标系将太阳系动力学中的哈密顿函数分为可积的三部分。Malhotra[42]研究伽利略卫星的潮汐演化时，将哈密顿系统分为了14个可积部分。Wu等人[43,44]令哈密顿函数的多部分分解更加一般化，将辛算法中的H0分成了N个子步，并用数值方法讨论了哈密顿在具有N+1个可积部分时的算法精度(主要是一阶和二阶)。

Wu等人[44]利用伯努利多项式[7]推出辛算法的哈密顿的误差函数：从哈密顿函数误差项出发，消去ε或ε2项，直接确定校正子C而不计算生成函数W，分别得到一阶辛校正和二阶辛校正。

(1)ε的一阶辛校正

由误差函数得到一阶辛校正算子[44]，从而消去截断误差项中εi的一阶项，一阶校正子的表达式为：

其中，A=L H0，B i=L Hi，互易子[A,B]=AB−BA，[A,B,C]=[A,[B,C]]，又记[A,B]=ℑAB，[A,A,B,C,C]=ℑ2AℑBℑCC，B(k)(x)是伯努利公式，满足递推公式[8]：

式(20)适用于有n个可积部分的哈密顿系统的任意阶辛算法，哈密顿的截断误差可以通过matlab或mathematica等数学软件直接确定[44]，提高了计算效率。

(2)ε的二阶辛校正

Wu等人[44]讨论了二阶显式辛算法S2X的二阶辛校正过程，该推导过程适用于一般n阶辛算法。S2X关于ε2的校正公式如下：

其中，

C2可用C¯2近似代替[44]。在太阳-木星-土星模型中，从能量误差、计算效率和平均经度误差方面进行数值比较，辛校正的计算精度比显式辛算法提高了一个量级并具有更好的数值稳定性。

3.2.2 类高阶辛算法

类高阶辛算法是在摄动分解的基础上形成高效的积分方法。相比较高阶辛算法的子步随时间步长的增加而迅速增加，类高阶辛算法的子步更少且计算效率更高。Chambers和Murison[7]从四阶和六阶辛算法出发，通过构造合适系数使误差项中不含ετ4或ετ6，构造过程如下：

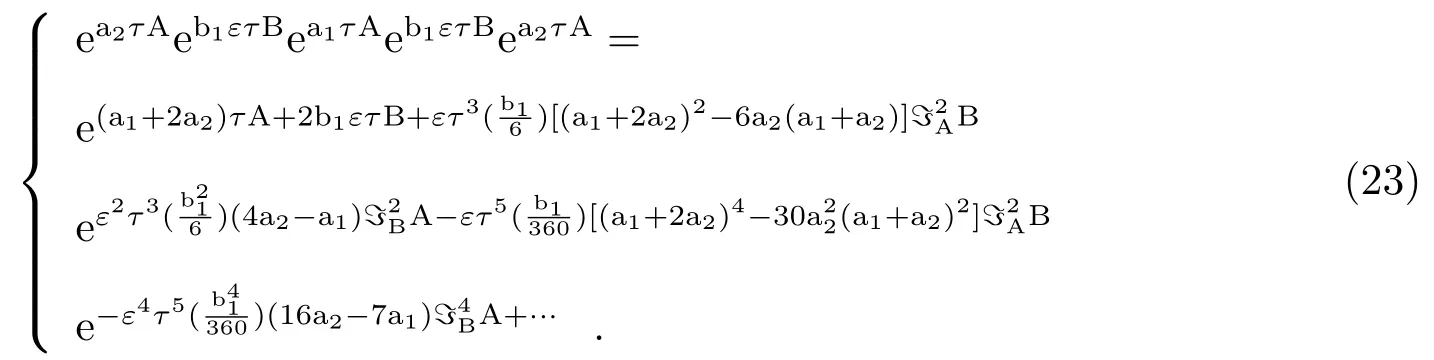
当

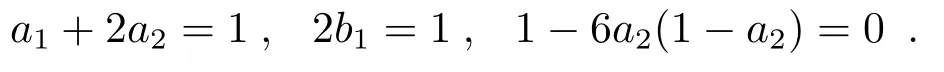
时，可消去ετ3项。

文中列举了类四阶辛算法和类六阶辛算法[7]：

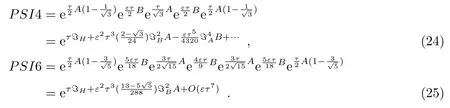
八阶和十阶等高阶算法也可被构造。从算法的构成特点看，类高阶辛算法能保持系统能量稳定[45,46]，计算效率也明显优于同阶的通常辛算法[11,39]。从算法的截断误差项来看，它可以看作是对二阶辛算法的部分校正。类高阶辛算法到达一定阶时，精度将不再随阶数的增加而提高。Laskar和Robutel[47]指出类六阶或八阶的数值效果最好。Wu等人[44]在日-木-土三体模型中对类四阶辛算法PSI4、它的校正算法及通常四阶辛算法S4三种算法进行数值模拟，结果表明三者的能量误差精度表现为同一量级。

4 力梯度辛算法

通常辛算法在积分过程中难免会出现负积分步长，但在不可逆的力学问题中需使得积分步长全为正。Ruth[2]在三阶辛算法的算子组合中引入力梯度算子使得每个积分子步的系数均为正。Chin等人[9,10,48–50]把力梯度辛算法发展到四阶，与同阶的非力梯度辛算法相比精度提高了10∼80倍[9]，在圆型限制性三体问题、含时引力场问题[10]及量子力学问题[48]中得到了很好的应用。Sun等人[51]在Chin提出的四阶力梯度辛算法基础上构造了两种含有三阶导数项的四阶力梯度辛算法，在Hnon-Heiles系统、四极矩核-壳模型以及含扁率限制性三体问题中进行数值模拟，精度和计算效率都得到了提高。Xu和Wu[52,53]应用这种力梯度辛算法求解摄动二体问题和雅可比坐标系下的摄动N体问题。Omelyan等人[54,55]将最优化思想引入到力梯度辛算法，按照对称组合的形式构造了三阶和四阶最优化力梯度辛算法，并将这两种方法运用到天体力学、分子动力学和量子力学等领域，与通常辛算法相比，数值精度得到了明显的改善，但是步长系数还是不可避免地用到了负数。李荣等人[12–14,56,57]构造了步长系数全为正步长的不对称的三阶、四阶最优化力梯度辛算法，这种方法在求解摄动开普勒混沌问题[57]的能量精度和定态薛定谔方程能量本征值问题中[12–14,56]表现出明显的精度优势。陈云龙和伍歆[15]论证了质心旋转坐标系中动能T不是动量P的严格二次型时，力梯度辛算法仍然适合求解。

定义力梯度算子为：

其中A、B如式(4)所设，将算子C与A、B算子组合可构造出力梯度辛算法：

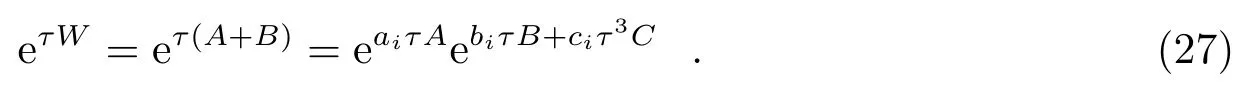
4.1 非优化力梯度辛算法

(1)三阶力梯度辛算法F3

这种算法的积分步长都为正，但力梯度算子C的计算过程较复杂，早期很少受到重视。

(2)四阶力梯度辛算法F4

Chin及其合作者在Ruth的基础上将力梯度辛算法发展到了四阶[9,10,48–50]，

与通常四阶辛算法相比，精度提高了10∼80倍。

Xu和Wu[52]按照Yoshida构造标准高阶辛算法的思路将算子C与A,B按照两种不同方式对称组合得到了两类新的四阶力梯度辛算法。

(a)力梯度算子嵌套在正中间时，表示为：

(b)力梯度算子嵌套在两端时，表示为：

根据BCH公式，从上式组合算子的中间开始实施循环推导得到W的具体表达式，由最优化思想得到一系列新的正积分系数，如表2和表3所示。A1和B1型算法对应于Chin的四阶C和D算法。Xu和Wu[52]用这两种新的四阶力梯度辛算法求解摄动开普勒问题和雅可比坐标系下的N体问题，以及深入研究了行星磁气圈内的带电粒子的混沌运动。如图2所示，两种分解形式中力梯度辛算法的数值性能没有明显差异，摄动分解形式中算法精度有显著提高。摄动分解形式中的力梯度算子的计算比计算H0更加简单，与H1相比不会增加大量额外的计算成本，所以是非常值得推荐其用于研究雅可比坐标系下的N体哈密顿问题[15,53]。

图2 FR和A,B两种类型四阶力梯度辛算法在两种哈密顿分解方式中的能量误差[53]

表2 A型四阶力梯度辛算法的几组正积分系数[53]

表3 B型四阶力梯度辛算法的几组正积分系数[53]

4.2 优化力梯度辛算法

(1)三阶最优化力梯度辛算法

Lie算子系数的求解只适用于对称辛算法，给不对称的力梯度辛算法的构造增加了困难。李荣等人构造了不对称的三阶和四阶最优力梯度辛算法[12–14,52]。根据Chin的思路，文中构造了如下的不对称算子组合：

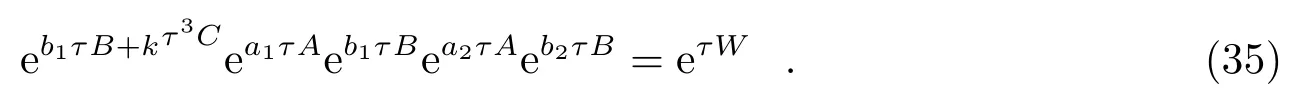
根据BCH公式得到阶条件的关系式，由最优化思想，即加入附加的约束条件[13](令其四阶截断误差系数平方和最小)，得到新的三阶最优化力梯度辛算法：

和

李荣[12]分别在谐振子模型、单摆模型、开普勒二体模型、Hnon-Heiles系统以及量子力学模型中对新构造的三阶最优化力梯度辛算法与其他辛算法进行数值比较。在经典力学模型中，该算法的能量误差计算占有绝对的精度优势，并且可以准确地识别Hnon-Heiles系统的混沌轨道，因此可以有效避免数值误差引起的虚假混沌现象。在定态薛定谔方程的能量本征值问题中，该算法同样有明显的精度优势，甚至与四阶标准辛算法相比具有更高精度。

(2)四阶最优化力梯度辛算法

Omelyan等人[54,55]构造的对称的四阶最优化力梯度辛算法如下：

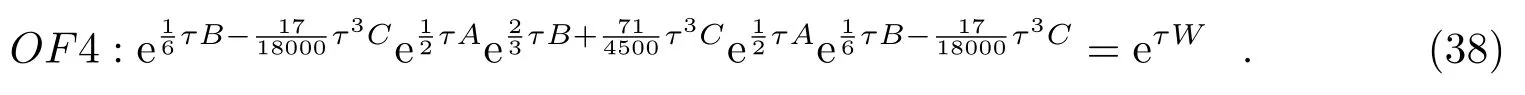
李荣[12]将得到的三阶最优化力梯度辛算法以对称组合的方式得到两个四阶辛算法，

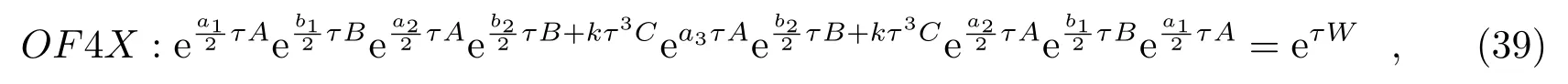
和

在开普勒二体问题和摄动二体问题等经典力学模型，以及量子力学模型中的Morse势模型中进行数值分析比较，新的四阶力梯度算法表现出了比较好的数值精度，甚至还要明显优越于已有的四阶最优化力梯度辛算法OF4[55]。

旋转坐标系中的平面圆型限制性三体问题的动能不是动量的严格二次型，而是受到旋转坐标系影响存在动量与坐标的交叉项，这给力梯度算子的加入带来了困难。陈云龙和伍歆[15]严格论证了力梯度算子在旋转坐标系中的形式仍与质心坐标中相同，均是引力的梯度而不是引力与非惯性力所得合力的梯度，只是将A算子变成了如下算子，式(26)中的C算子仍然适用，

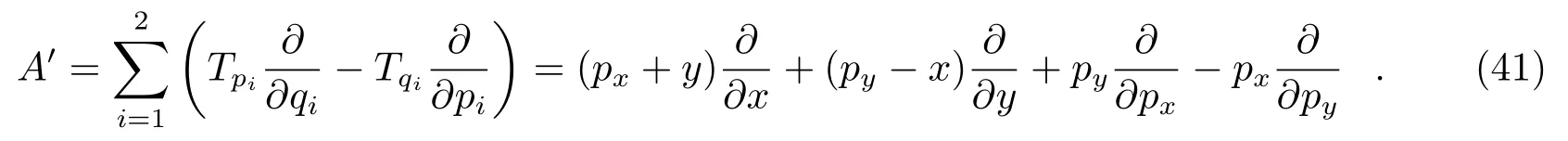
应用四阶力梯度辛算法、最优化四阶力梯度辛算法和Forest-Ruth辛算法分别求解该问题，数值结果显示最优化四阶力梯度辛算法能够取得最好精度。

5 隐式辛算法

5.1 隐式辛算法的构造

当系统的哈密顿变量不可分离时，显式算法一般无法直接应用。考虑不可分离哈密顿函数：

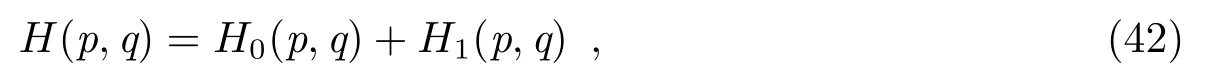
与3.2节中的约定类似，约定Lie算子A={,H0}和B={,H1}。

正则方程表示为：

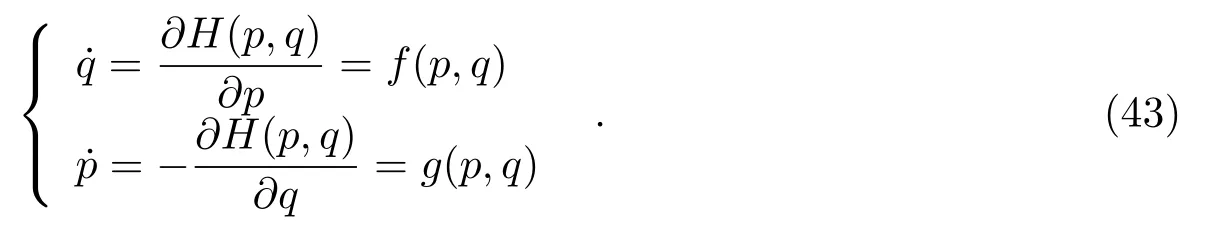
以时间τ为步长，对整个哈密顿系统按照一阶Euler部分向前差分公式，得到一阶隐式辛算法M1和M∗1、二阶隐式中点法M2[2]：

(1)一阶位置隐式Euler法

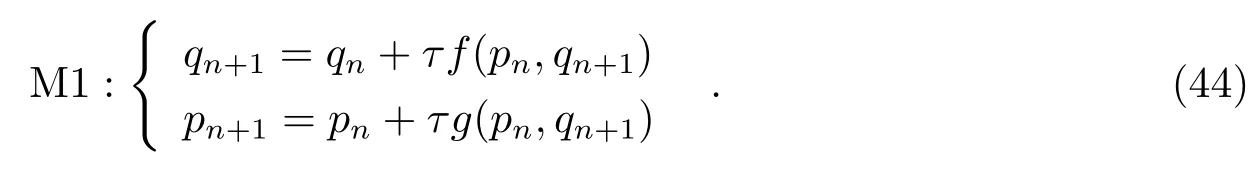
(2)一阶动量隐式Euler法

(3)二阶隐式中点法

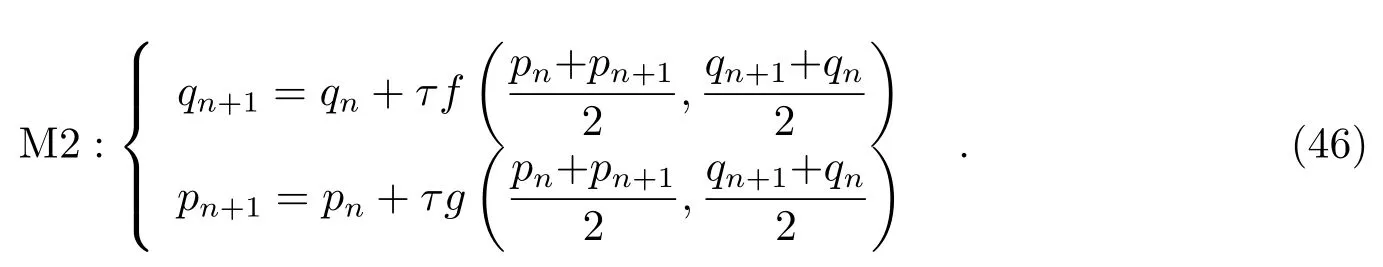
(4)二阶显隐混合辛算法

A算子是有解析解的算子，而B是隐式中点法迭代求解的算子，两者结合组成：

(5)高阶隐式辛算法

按照Yoshida[5]和Ruth[2]构造高阶显式辛算法的思路对全局哈密顿函数构造高阶隐式辛算法：

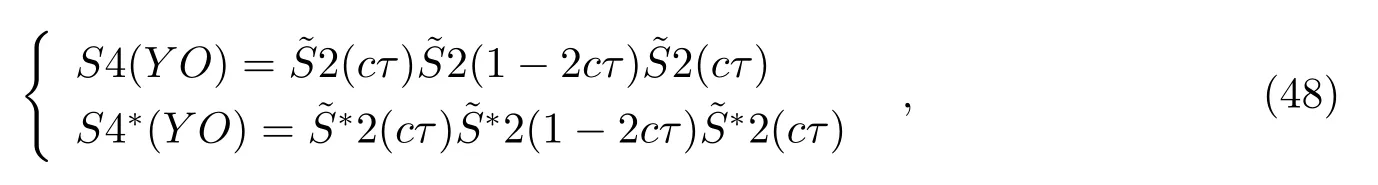
和

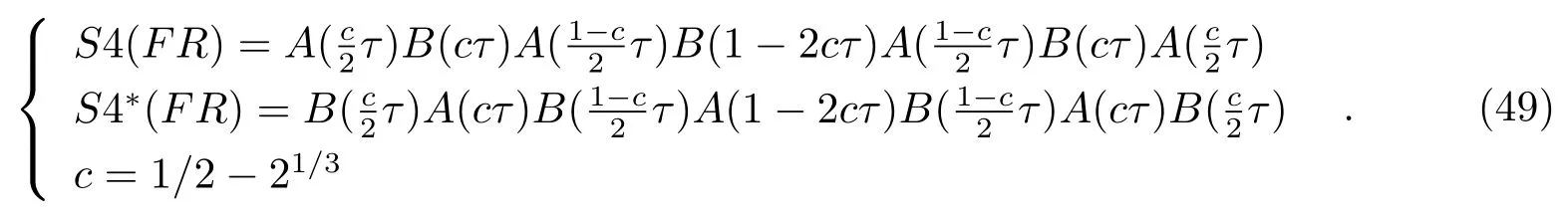
全局隐式辛算法使计算效率不理想。若通过变量分离使得H0可积，H1不可积，再根据式(44)―(46)构造显隐式混合辛算法，显然显隐式混合辛算法的效率要高于全隐辛算法。

Zhong等人[18–21]将二阶隐式中点法及其对称组合运用求解整个后牛顿哈密顿系统，数值试验表明，显隐混合中点嵌入法在能量精度方面始终优于全隐中点法，且前者的计算效率更好。Zhong和Wu[19]另外对中点嵌入法进行优化，进一步提高了计算精度。对于自旋后牛顿哈密顿系统：

开普勒部分和后牛顿部分分别表示为：

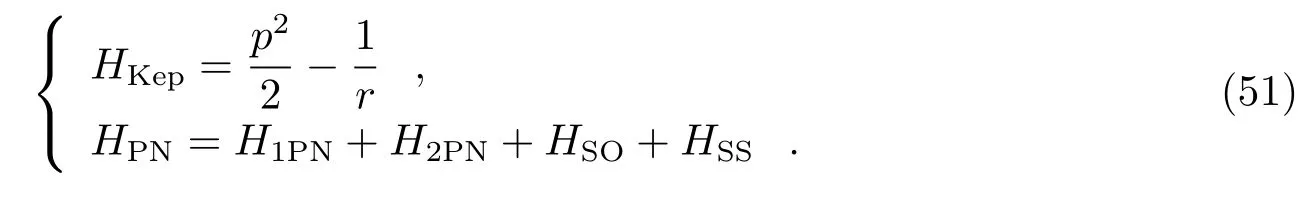
对旋转标量引入Wu和Xie[18]的正则旋转坐标，得到新的正则哈密顿函数Γ(r,θ,p,ξ)，将隐式中点法直接应用于求解变量Γ(r,θ,p,ξ)，记作S2A。另外，Zhong和Wu[19]分别对开普勒部分和后牛顿部分求解析解和数值解，数值解部分应用隐式中点法，按照Yoshida的思路构建四阶正则显隐式混合辛算法：

Mei等人[22,23]对四阶Forest-Ruth型显隐混合辛算法和四阶Yoshida显隐混合辛算法进行理论分析，证明前一种算法在大多数情况下只有二阶精度，后者可以达到四阶精度。在一维不可分系统和致密双星后牛顿哈密顿系统中得到了相同的结论。他们指出，在实际计算中，当哈密顿的部分变量可积且解析解容易获得时，应采用S4(FR)算法或将解析解与隐式数值解结合的Yoshida算法S4(YO)，以获得较高的计算精度和效率。当可分哈密顿的变量部分可积，但其解析解难以求解，或者哈密顿变量部分不可积，则采用将解析解与隐式数值解结合的Yoshida算法S4(YO)。

Lubich等人[58]提出了四阶非正则的显隐式混合辛算法，主要在自旋致密双星后牛顿哈密顿系统中应用，将哈密顿分成了三大部分，分别是轨道HOrb、自旋−轨道HSO和自旋−自旋HSS：

按照Suzuki[17]用二阶积分器的五重积构建四阶算法的思路构造如下算法：

再分别将这三部分分解为2,3,4部分运用显隐式混合辛算法求解。将式(54)发展到四阶：

5.2 几种隐式辛算法的数值稳定性比较

当哈密顿两部分均可积时，刘福窑等人[59]分别对上述一阶隐式辛算法M∗1、隐式中点法M2以及一阶显式算法，二阶显式算法四种算法的数值稳定性进行分析比较，将这几种算法作用于线性哈密顿系统：

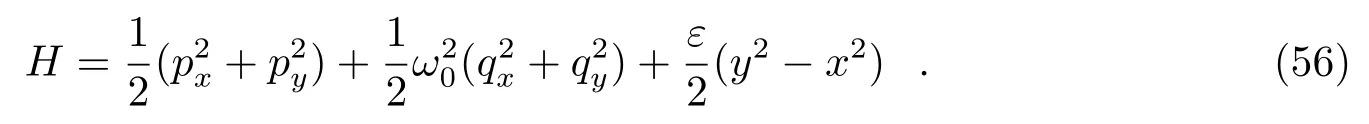
与T+V分解相比，H0+εH1分解中各算法的稳定区域扩大了。2009年，刘福窑和钱晓明[60]比较了Liao[16]提出的两种显隐混合辛算法的数值稳定性，即将一阶隐式辛算法M∗1和隐式中点法M2分别嵌入到一阶和二阶显辛算法中得到显隐混合辛算法，前者的数值稳定性要优于后者。

钟双英[61]分别以一维耦合振子、经典圆型限制性三体问题和后牛顿近似的致密双星系统为数值研究对象，对显隐混合辛算法MSI1和MSI2的数值优劣性能进行比较。一维耦合振子模型和圆型限制性三体问题中MSI2算法的稳定性均要明显优于MSI1算法。两种算法在不同的哈密顿分解形式中表现有很大不同，在T+V分解中，两种嵌入法都能保持数值稳定；在H0+H1分解中，MSI1算法在有序轨道和混沌轨道中均不能保持数值稳定。自旋致密双星后牛顿哈密顿系统中，MSI1算法的计算效率比MSI2算法稍高，但稳定性不如MSI2算法。综合诸因素可知，中点嵌入法更适合于求解各种相对论后牛顿动力学问题。

隐辛算法适用于任何哈密顿系统，尤其在使用经典算法表现出较差的稳定性时，隐辛算法是理想的选择，但是求解过程中由于迭代使得计算效率大大降低，因此应尽量不要作为首选数值方法。

6 扩展相空间显辛算法

Pihajoki[24]提出一种相空间扩充方法。在不可分离的哈密顿系统中分别增加一组与原空间相同的动量和坐标得到一个新的可分离的哈密顿量：

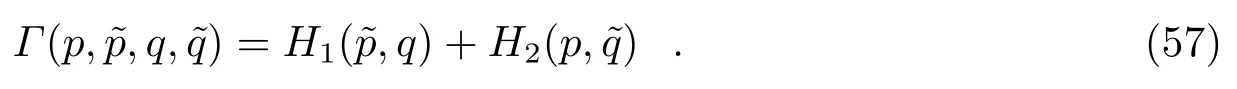
上式右边的两部分相互独立且可积，可以分别进行解析求解，由正则方程得到：

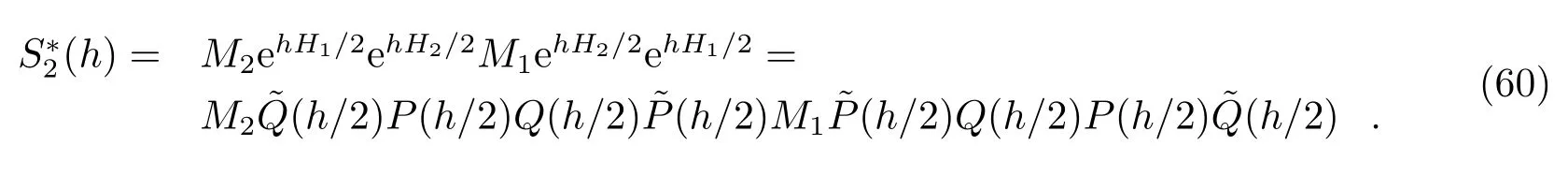
或

其中，M1,M2表示两组变量之间的置换映射，即：

此外，需借助投影算符W将扩展相空间的解返回到原始相空间，

6.1 高阶连续坐标动量置换相空间扩充显式类辛算法

Liu和Wu[26]用偶数重积构建了不同于Yoshida构建高阶辛算法思路的显式高阶类辛算法，用六个偶数低阶算法构造高阶算法S4A：

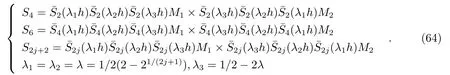
这种构建模式由四部分组成：置换坐标，没有置换的三个偶数低阶蛙跳格式的积分，置换动量，没有置换的三个偶数低阶蛙跳格式的积分[26]。

在平面圆型限制性三体问题、Chin[9]考虑的简单模型和无旋转致密双星的后牛顿哈密顿系统中，高阶连续坐标动量置换相空间扩充显式类辛算法在数值精度上优于Yoshida的四阶显式辛算法、Chin[9]的显式辛算法以及显隐式混合辛算法，计算效率也远远高于显隐式混合辛算法。这类显式类辛算法也适合求解后牛顿哈密顿问题和旋转哈密顿问题等坐标和动量不可分离的哈密顿系统。

6.2 中点置换相空间扩充显式类辛算法

Liu和Wu[26]提出的高阶类辛算法需要进行两次三重积才能达到高精度效果，且在旋转致密双星后牛顿哈密顿系统的某些轨道积分中会失败[52]。骆俊杰等人[28,29]将连续坐标动量置换改为一次中点置换(原变量与它对应扩展变量之间的中点)，每一步积分都调整原变量及其对应扩展变量的值为他们的中点值，即：

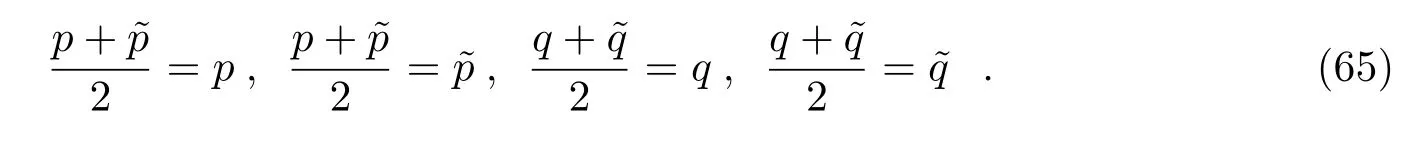
再结合Yoshida的三重积构造高阶类辛算法S4B：

以不考虑引力耗散的二阶后牛顿近似的自旋致密双星为模型，在周期轨道和混沌轨道中，新构造的中点置换相空间扩充法S4B的数值精度与隐式中点法IM4、连续坐标动量置换相空间扩充法S4A相比最高。在混沌轨道中，连续坐标动量置换相空间扩充法S4A在积分一半时间时产生了剧烈的误差偏移。由于H1,H2的不同，在混沌轨道中，使得S4A在置换过程中两部分哈密顿函数的误差不停积累导致失效。

中点置换法可以推广到非保守的引力耗散哈密顿系统中，分别以引力耗散的2.5PN后牛顿近似的自旋致密双星、阻尼谐振子和受到Poynying-Robertson阻力的尘埃粒子为模型，中点置换法仍然保持了最佳的优越性，该方法的计算精度、计算效率以及普适性都优于其他算法，值得被推广使用。

6.3 扩大相空间FR最优化算法

吴亚林等人结合优化思想和扩充相空间的思想，构造了几种优化的相空间扩充类辛算法；并分别在一维不可分可积系统、平面圆型限制性三体问题、三阶后牛顿致密双星系统中与其它辛算法进行了数值比较[30,62]。

6.3.1 几种扩充相空间类辛算法

(1)连续坐标动量置换扩充相空间优化算法

将FR算法和其优化算法OFR中间算子按照Liu和Wu[26]构造的高阶类辛算法进行拆分，分别将(10)式和(16)式改造为：

(2)中点置换扩充相空间优化算法

按照骆俊杰[29]提出的中点置换法将式(10),(11),(16),(17)分别改造为：

(3)Tao保辛显式算法

Tao[25]改造了Pihajoki的方法，将不可分哈密顿系统改造为：

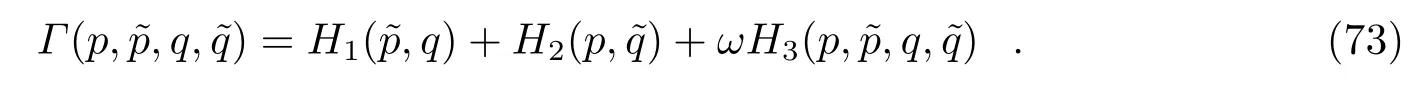
上式ωH3部分是Tao人为增加的约束哈密顿函数，ω是控制新旧相空间变量之间间隔的参数，H1和H2有解析解，上文第二节中给出的算子A,B算子仍然适用，H3部分可积。这里再令算子B¯为：

其中D算子是H3部分的算子。得到新的二阶显式辛算法：

吴亚林等人对FR算法以及Suziki算法用Tao的方法进行改造得：

由于算法中没有加入置换因子，算法的辛结构将不会被破坏，ωH3起到约束和调节新旧空间变量的作用，ω的选取对精度将产生很大的影响。

6.3.2 算法的数值检验

分别在一维不可分哈密顿系统、平面圆型限制性三体问题和三阶后牛顿非自旋致密双星系统中对以上算法数值比较，精度由高到低是M OFR≈M SU>M FR≈M YO>IM4>EOFR≈TSU>EFR≈TYO。总的来说，优化后的算法比未优化的精度高，各算法与中点置换结合比与Tao法结合精度高，能达到优化四阶通常显辛算法的精度，且四阶隐式辛算法的计算效率最低。TSU算法与系数ω有关，ω=100时精度达到四阶精度。

6.4 扩大相空间的对数哈密顿显式对称法

对数哈密顿辛算法在解决高偏心率轨道问题时可以通过调节步长避免数值失真，构造过程较一般的时间变换辛算法更简单。扩大相空间使得显式辛算法可以应用于不可分哈密顿系统，且精度理想。Li和Wu[31,63]结合这两种思想，在Mikkola等人[32,64,65]提出的对数哈密顿方法的基础上加上一个常数或者函数，再结合Pihajoki的相空间扩充思想，构造了适用范围更广的扩充相空间的对数哈密顿类辛算法，它的基本的哈密顿形式为：

其中，p0=−H，q0=t，C为积分常数，参数C>0。当C=0时，是Mikkola以及苏湘宁[66]所构建和使用的对数哈密顿方法。时间变换函数g=T+p0+C和g=U+C。哈密顿的动能和势能部分可分时，一般的显式辛算法可以使用；两者不可分时，扩充相空间的思想可以被考虑。

6.4.1 扩大相空间的对数哈密顿辛算法

根据系统显含时间t和不显含时间t可将哈密顿函数分别扩充为：

(1)不显含时间

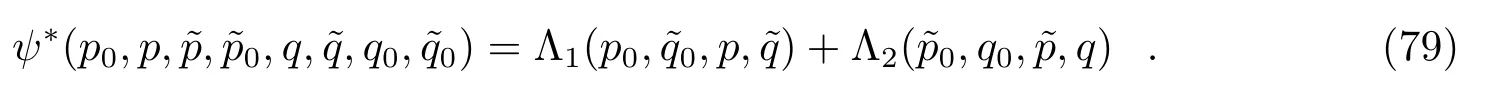
6.4.2 数值检验

将四阶显式辛算法FR、四阶隐式中点法IS4(与6.3.2节中的IM4相同)及三种扩充相空间算法S4A,S4B,S4C分别应用求解开普勒摄动二体问题、圆型限制性三体问题和无自旋三阶后牛顿致密双星系统。在三种模型中，S4C算法的表现始终是最好的，隐式中点法IS4算法虽然也表现出了很好的计算精度，但是在计算成本上最高；S4B算法与IS4算法精度同量级且计算成本最低。扩大相空间的对数哈密顿显式类辛算法在数值稳定性、数值精度以及计算效率上均占有很大的优势，且适用于高偏心率轨道。本文主要在圆型限制性三体问题中对以上算法进行数值比较，这几种算法分别是四阶显式辛算法FR、四阶隐式中点法IS4、连续坐标动量置换相空间扩充显式算法EFR及优化算法EOFR、中点置换相空间扩充显式算法MFR及优化算法MOFR。如图3所示，对于低偏心率轨道，四阶显式辛算法FR在长时间积分过程中能保持能量误差稳定且精度较高，但在高偏心率轨道中，FR算法在长时间积分后能量误差开始增长。c=0时，连续坐标动量置换EFR四阶算法与其优化算法EOFR均不适用于高偏心率轨道，它们在较短时间误差就开始增长。c=1.7时，各相空间扩大法的精度均有提高，且EFR算法和EOFR算法在高偏心率轨道中使得能量误差不再线性增长，说明系数c的选取很重要。另外，中点置换相空间扩大法MFR及其优化算法MOFR的计算效率最高，四阶隐式算法IS4的计算效率最低。

图3 圆型限制性三体问题中的两条轨道的能量误差

7 总结与展望

辛算法自从被提出以来，特别是可分哈密顿系统的显式辛算法，在动力学天文中被广泛应用，已充分显示出传统算法不可比拟的优点。在定量天文学计算问题中，辛算法可以有效控制轨道沿迹误差的持续快速增长，但是对于同阶算法，辛算法的截断误差要比Runge-Kutta法等传统方法大，在较短时间内优点无法突出。辛校正和类高阶辛算法则通过误差校正，在不缩小积分步长的前提下使得算法精度提高，时间变化辛算法使用变步长，解决了天体紧密交会和大偏心率轨道中的数值解失真问题。对于不可分哈密顿系统，隐式辛算法非常适合应用，与传统算法相比，它也能保证系统的辛结构和能量误差稳定，但积分过程由于多次迭代使得计算效率显著降低。扩大相空间的类辛算法近年来得到了快速的发展，其中Luo等人[28,29]构造的中点置换扩充相空间方法是目前最理想的，它具有高精度、高效率和高适用范围，之后提出的扩大相空间FR最优化算法[30,62]以及扩大相空间对数哈密顿显式类辛算法[31,63]都对此进行了证明。力梯度辛算法作为一种独特的辛算法，在时间可逆的哈密顿系统求解中具有很大的优势，但在哈密顿变量不可分时应用有困难。