轴向运动梁动力学研究综述

2021-07-13段应昌段壮志

兵器装备工程学报 2021年6期

段应昌，段壮志，刘义，刘虎

(陆军工程大学训练基地，江苏徐州 221004)

自然界和工程技术中，轴向运动梁的运用十分普遍，广泛存在于军事、航空航天、土木、电子、机械和汽车等工程中。

火炮射击时弹丸在膛内高压燃气的推动下沿身管向炮口高速运动，身管在后坐力的作用下沿摇架后坐，同时伴随着剧烈的振动，火炮在这种强冲击载荷作用下的振动控制一直是火炮工程界所关心的问题。现代火炮普遍采用具有反后坐装置的弹性炮架，包括摇架在内的架体部分在射击时保持静止不动，而身管沿着摇架导轨作轴向后坐和复进运动，因此可以把摇架考虑为固定基座，身管后坐运动过程的结构体系可简化为轴向运动悬臂梁[1]。

除此之外，架桥车推出导梁和桥跨、航天器展开的附件、机器人伸展的手臂、伸缩的硬式空中加油管、轧制钢带等多种系统工程元件，在适当的假设条件下都可以模型化为轴向运动悬臂或简支梁模型。这类结构的横向振动问题对生产的产品质量或作业过程的安全性和可靠性会产生重要影响，物质的轴向运动会诱发其产生横向振动并可能导致失稳。例如，火炮射击过程身管的振动响应，对火炮射击的精度有重要影响；平推式架桥车的桥体向前移动时，桥体的振动直接影响架桥速度与工程保障效率；带锯的振动导致较差的切削质量，甚至导致带锯结构的破坏；在航天器附件展开时，其横向振动直接影响机构运作精度以及结构可靠性；硬式空中加油管伸缩时，加油管的振动直接影响加油管与受油飞机的对接平稳性和可靠性；军用的雷达天线在伸出时，天线的横向振动对结构的强度和作战效率有着重要的影响[2]。

综上所述，研究轴向运动梁的横向振动对这些工程设备的设计及使用尤为重要，这一类问题具有广泛的工程背景，而且其横向振动在理论求解和实际控制上也存在着较大的难度，受到了众多研究者的关注，该类问题已成为国内外研究的一个热点。

1 轴向运动梁线性动力学研究现状

轴向运动体梁广泛存在于军事、航空航天、土木、电子、机械和纺织等工程中，在研究中根据边界条件的不同简化为相应的结构模型。Mote[3-4]在20世纪60年代首先开展了轴向运动体系振动特性的研究，并对影响结构稳定性的因素进行了分析。Stylianou和Tabarrok[5，6]建立了单元数目不变、单元长度随时间改变的有限元模型，说明了该模型在轴向运动梁动力响应求解中的运用，进而研究了轴向运动梁动力稳定性问题。Al-Bedoor和Khulief[7，8]采用系统方法得到了不同边界条件下轴向运动梁横向振动的近似解析解。Fung等[9]运用Hamilton原理推导了端部带有集中质量的伸展梁的振动方程，建立了Timoshenko、Euler、simple-flexible和rigid-body四类轴向运动梁的动力学模型，并分别讨论了它们的振动特性。Öz和Pakdemirli[10]研究了速度以正弦规律变化的轴向运动梁的动态响应，发现当梁的速度变化频率接近结构固有频率的2倍或为其中两阶频率之和时，系统会发生失稳。

进入21世纪后，轴向运动体系动力学建模及其稳定性的研究都有了较深入的发展，尤其在求解方法上取得了较大的进步，这些方法主要包括Galerkin法、假定模态法、有限元法、格林函数法、多尺度法、渐近法、Laplace变换法和谱元法(spectral element method)等。Zhu和Ni[11]研究了水平和竖向运动的梁和弦线的动力稳定性特征。Zhu等[12]运用扩展的Hamilton原理分别推导了自由端附加集中质量且包含控制力和力矩的轴向运动梁和弦的振动方程，在假定模态的条件下采用修正的Galerkin法将振动偏微分方程离散为常微分方程；他们还建立了基于Lyapunov稳定准则的轴向运动体系振动控制系统；在此基础上，他们首先比较了无轴向控制时端部质量对悬臂梁伸展和收缩运动时振动响应和机械能的影响，发现端部质量对梁的轴向收缩运动起稳定作用；其次分析了振动控制方法对轴向伸展和收缩运动梁动力响应的影响，结果表明存在最优的控制法则可将结构伸展或收缩过程中的振动能量完全耗散。Öz等[13]使用多尺度法得到了变速轴向运动梁的非线性振动方程的近似解。Pellicano和Vestroni[14]研究了简谐激励下高速轴向运动简支梁的动态响应，他们的研究拓展了对高速轴向运动梁振动特性的了解。Ozkaya和Pakdemirli[15]采用匹配渐近展开法和多尺度法研究了轴向运动梁的振动问题，得到的解均为非共振解。Ozkaya和Öz[16]使用人工神经网络方法确定了轴向运动梁的固有频率和振动的稳定区域。Oh和Lee等[17-18]提出了拉力作用下的轴向运动Euler梁和Timoshenko梁的谱元模型，研究了轴向速度和拉力对梁的振动特性、频散关系和稳定性的影响。早期的大部分文献基本都忽略了轴向运动体系支撑点前方或后方结构对系统振动的影响，Lee和Jang[19]采用谱元法研究了半无限轴向运动梁的振动特性和稳定性，数值分析表明考虑支撑体前后结构的影响能够更准确的预测结构系统的动力特征。Chang等[20]运用单元长度变化的有限元法研究了轴向运动Rayleigh梁的振动特性和稳定性，对于细长梁来说采用Rayleigh梁模型比Euler梁模型更准确。

众所周知，结构都具有黏性，结构的黏性能够减小系统振动的幅度。在一些特殊情况下，结构的黏性是系统的主要特征，部分学者已经对轴向运动体系的黏性进行了考虑。Lee和Oh[21]建立了轴向拉力作用下的轴向运动黏弹性梁的动态响应和稳定性分析的谱元模型，进而研究了材料的黏弹性和速度对轴向运动梁动态响应和稳定性的影响。Ghayesh和Balar[22]对轴向运动黏弹性Rayleigh梁进行了非线性参数振动和稳定性研究。Yang等[23]根据Newton第二定律得到了多频激励作用下的轴向运动黏弹性梁的非线性偏微分方程，采用一阶Galerkin截断法对偏微分方程离散求解。Liu等[24]研究了随机无序周期性激励作用下的轴向运动黏弹性梁的动态响应，采用多尺度法得到了振动方程一阶展开解析表达式。基于平板理论和Kelvin-Voigt黏弹性模型，Saksa等[25]采用经典模态分析法研究了轴向运动黏弹性板的动态响应和稳定性。Ghayesh等[26]采用数值方法研究了轴向运动黏弹性梁纵向和横向的非线性受迫振动。

国内对轴向运动体系振动特性的研究开展相对较晚，但一些学者对轴向运动悬臂梁动力响应及振动控制的研究具有较强的借鉴意义。朱桂东等[27-28]将空间飞行器柔性附近的伸展简化为伸展悬臂梁模型，采用Lagrange方法推导了该模型的动力学方程，由悬臂梁特征函数对方程进行了离散求解，分析了悬臂梁伸展规律及外界激励对系统动态响应的影响，为实际工程结构伸展规律设计打下了理论基础。李俊峰和王照林[29]建立了带挠性伸展附件的航天器伸展动力学模型，并研究了附件按指数规律仲展和幂次规律伸展的弹性振动对航天器姿态的影响，得到了姿态角速率的渐近公式。基于小变形假设，张洪华[30]对绳系卫星附件伸缩运动稳定性进行了研究，结果表明伸展运动会增加结构的稳定性，但收缩运动会使结构稳定性下降。程绪铎等[31]推导了航天器柔性伸展梁的动力学方程，由Runge-Kutta积分法得到了方程的数值解，数值分析了初始振动对梁的伸展运动和姿态运动的影响以及姿态角速率对梁的伸展运动和振动的影响。邓子辰等[32]针对时变结构提出了一套计算精度高、数值稳定性好的计算方法—精细积分法，并用该方法研究了伸展悬臂梁在不同伸展规律下的动态特性，通过与已有文献结果对比验证了精细积分法处理时变动力学问题的可行性。李山虎等[33]建立了独立模态控制下的伸展梁动力学方程，利用多尺度法得到了方程的近似理论解；在此基础上，计算了悬臂梁在有无控制力下伸展时的梁端位移响应，计算结果与早期的有限元结果吻合。牛春燕[34]根据Hamilton原理建立了伸展粘弹性悬臂梁的动力学方程，由方程分析了有无外荷载作用下粘弹性梁按匀速伸展、加速伸展和指数规律伸展时的动态特性，并与弹性伸展梁的动态特性对比，结果表明粘性系数对梁的稳态振幅影响较大。王亮等[2，35，36]利用D’Alembert原理得到了轴向运动悬臂梁的振动方程，采用修正的Galerkin法对方程进行求解，并设计制造了轴向运动悬臂梁试验平台来验证理论模型的正确性。刘宁和杨国来[1]将火炮发射系统简化为移动质量作用下的轴向运动悬臂梁系统，采用D’Alembert原理推导了系统的振动方程，使用修正的Galerkin法对方程进行了求解。通过计算表明，移动质量主要激发梁的一阶模态，进而分析了移动质量的大小和运动速度对梁动力响应及稳定性的影响。段应昌等[37-38]建立了简谐激励作用下轴向运动嵌套悬臂梁和轴向运动嵌套固支-简支梁横向动力响应理论计算模型，通过模型试验进行了验证。

轴向运动悬臂梁模型[1-2，12，33，35-36]的线性动力学是学者研究比较普遍的一种简化模型，该模型是其他复杂模型研究的基础，如图1所示。图中悬臂梁任一时刻的长度为l(t)，抗弯刚度为EI(x)，单位长度质量为m(x)，梁的竖向位移为y(x，t)；梁的轴向运动速度为u(t)，阻尼系数为c(x)。

图1 轴向运动悬臂梁模型示意图

根据D’Alembert原理[37-38]建立轴向运动嵌套悬臂梁的横向振动方程为：

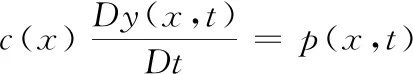
(1)

文献中通常采用修正Galerkin法[1-2，12，35-36]对方程(1)进行求解，也可采用多尺度法[33]进行求解；采用修正Galerkin法对方程进行线性离散求解[1-2，12，35-36]，最终可得离散微分方程为：

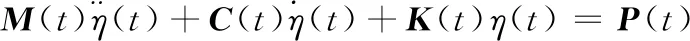
(2)

式中：η(t)为广义坐标；M(t)为质量矩阵；C(t)为阻尼矩阵；K(t)为刚度矩阵；P(t)为载荷向量。

上述研究中刘宁和杨国来[1]采用修正的Galerkin法离散求解了移动质量作用下轴向运动悬臂梁的振动方程，该方法概念清晰，易于理解，但没有进行实验验证；王亮等[2，35-36]采用较复杂的横向振动位移表达式离散求解了振动方程，设计了轴向运动悬臂梁实验平台，通过平台研究了轴向运动悬臂梁的阻尼与边界条件等效建模方法，但实验结果与修正后的理论计算结果偏差较大。本文作者结合文献[1-2，35-36]的研究，得到悬臂梁伸展速度为1.327 cm/s时梁端加速度响应修正后的理论计算结果和实验结果如图2所示。从图中可以看出，修正后的理论结果与实验结果基本相符，验证了理论计算模型的正确性[37-38]，由此给出了研究轴向运动悬臂梁动力学的一种基本方法。

图2 伸展速度为1.327 cm/s时梁端加速度响应理论计算结果与实验结果曲线

2 轴向运动梁非线性动力学研究现状

上述轴向运动体系动力学研究的综述主要集中在线性振动的成果上，只有少部分包括了非线性振动内容。线性振动分析无法解释振幅大或在临界速度附近出现的自激振动、参数振动、跳跃问题、内共振、组合谐波共振、次谐波共振和超谐波共振等非线性振动现象，为此学者对轴向运动体系的非线性振动问题开展了大量的研究。Mote[39]首先提出了轴向运动体系的非线性振动问题，并分析了轴向运动带的非线性振动，通过研究发现线性振动分析只限于解决张力较大、速度小的问题。Thurman和Mote[40]最先建立了完整的轴向运动带的非线性振动方程。Elmaraghy和Tabarrok[41]研究了轴向加速运动Euler梁的参数共振。Wickert和Mote[42]利用特征函数法研究了轴向运动体系的横向非线性振动。Parker和Lin[43]采用一阶Galerkin离散和摄动法研究了张力波动的轴向运动梁的动态稳定性。Riedel和Tan[44]利用多尺度法研究了轴向运动带的内共振问题。冯志华和胡海岩[45]研究了两端简支运动Euler梁发生3∶1内共振时的参激振动的平凡解稳定性进行了详尽的分析，他们还在文献[46-47]中详细研究了两端简支运动Euler梁的参激振动引起的非线性动力学行为。吴俊和陈立群[48]利用Hamilton原理建立了轴向运动弦线的非线性偏微分方程，使用多尺度法对方程进行求解，由Liapunov线性化稳定性理论导出了倍频参数共振时平凡解和非平凡解的不稳定条件。陈树辉等[49-50]分别采用增量谐波平衡法(the incremental harmonic balance method，IHB)和多元Lindstedt-Poincare(L-P)法研究了轴向运动梁横向非线性振动的内部共振，研究表明在小振幅的情况下，2种方法的数值结果是一致的。黄建亮[51]应用多元L-P法和IHB法研究了轴向运动体系的横向非线性振动，揭示了基谐波响应、次谐波响应、超谐波响应和组合谐波响应等非线性振动现象。基于上述的研究，黄建亮和陈树辉还在文献[52-56]中研究了不同因素影响下轴向运动体系的内共振、联合共振、纵横向耦合振动等复杂而有趣的非线性现象。Chen和Yang[57]研究了轴向加速运动黏弹性梁参数共振的稳定性。Tang等[58]分析了不同边界条件下轴向运动Timoshenko梁模型的固有频率、模态和临界速度。Pakdemirli和Öz[59]采用多尺度法得到了两端简支轴向运动梁横向振动的近似解析解，截取梁的四阶模态对梁的共振进行了详细分析。杨晓东[60]采用平均法、多尺度法、Galerkin法和数值方法等分析了轴向运动梁的次谐波共振失稳、分岔问题、跳跃现象及混沌运动等非线性振动问题。丁虎[61]研究了轴向运动黏弹性弦线和梁横向非线性振动的建模、分析和仿真，从理论上证明了在轴向运动黏弹性梁的受迫振动以及参数振动中不参与共振的模态不影响主谐波共振和亚谐波共振的稳定性或稳态响应。王波[62]采用渐近摄动法和微分求积法研究了轴向运动黏弹性梁的线性参数振动和非线性参数振动问题。唐有绮[63]采用近似解析分析和数值计算结果相互验证的方式对轴向运动Euler梁、Timoshenko梁和面内平动板3种模型的横向线性振动和非线性振动进行了系统的研究。Yang等[64]研究了两端简支轴向加速Timoshenko梁模型的参数振动稳定性，数值分析了速度、弯曲刚度、转动惯量和剪切模量对失稳边界的影响。Ding和Chen[65]通过快速傅里叶(FFT)法研究了轴向运动梁非线性平面振动的固有频率。Ghayesh等[66]研究了轴向运动梁3∶1内共振情况下的纵横向耦合非线性强迫振动问题。Zhang等[67]重点研究了超临界速度下轴向运动黏弹性梁强迫振动的稳态周期响应。黄玲璐等[68]采用Kelvin本构关系建立了轴向运动黏弹性梁动力学模型，将直接多尺度法应用于内共振和外部激励下的轴向运动黏弹性梁横向非线性受迫振动的稳态响应。李炀等[69]推导得到了外部激励作用下两端带有弹簧支撑的轴向运动梁的振动方程，然后通过数值方法研究了系统的固有频率、模态、临界速度等参数特性。周远等[70]应用直接多尺度法和微分求积法研究了简支边界条件下黏弹性阻尼作用的轴向运动Timoshenko梁的横向振动特性，得出了梁的固有频率和衰减系数与黏弹性系数的变化关系。

3 轴向运动结构振动控制研究现状

对轴向运动的工程结构进行振动控制主要包括2个方面：一是提出轴向运动速度控制策略；二是从结构本身出发给出振动控制的方法。Zhu等[12]对变长度运动结构的振动稳定性和控制问题进行了研究。Chang等[20]研究了匀速伸展梁和周期伸缩运动梁的稳定性，对于匀速伸展梁，由特征方程可以确定不同速度下梁的稳定性，研究发现较快的伸展速度会使梁在较短的伸出长度下就发生失稳，可由特征方程的实部和虚部确定的稳定区域来控制伸展速度；对于周期伸缩运动梁则采用Floquet理论来研究梁的稳定性，分别探讨了梁的振幅和伸缩频率对稳定性的影响。

结构振动控制技术是指在结构上安装控制系统，当结构受外界激励发生振动时，控制系统将给结构提供被动或主动控制力，以达到减小结构振动的目的，从而满足结构的安全性和适用性等功能要求[71]。王亮等[2，36]使用永磁铁对铁质轴向运动悬臂梁进行横向振动的主动控制。结构体系固定不变的系统的振动控制技术研究成果很丰富，已有的研究包括不需要外界能量输入的被动控制技术，需要动力驱动的主动控制技术和主被动控制相结合的一体化控制技术[72]。但类似于固定结构体系振动的主、被动控制技术研究还较少，将成为研究的热点。