基于波叠加近场声全息射线波函数的信息补偿

陈岩豪 向宇 石梓玉

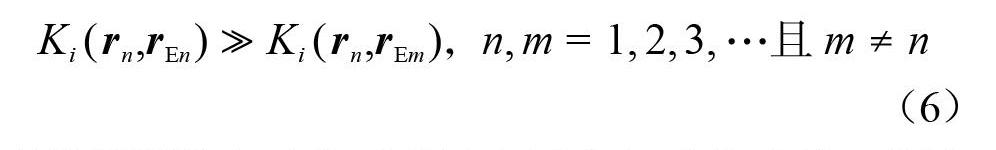
摘  要：基于波叠加法的近场声全息技术因其在适应性和数值计算上的优势，近年来已经被广泛应用于声源识别、定位和声场分析.在基于波叠加法的近场声全息技术中，以射线波函数为波叠加法的积分核函数可有效改善系统矩阵的病态性，提高声场计算的数值稳定性.但由于射线波函數在低波数处的指向性过强，声场信息主要集中在射线波函数的主指向处，导致了其他方位的声场信息缺失.针对以上问题，提出了一种射线波函数信息的补偿方法，即在射线波函数中加入一定比例的单极子球波函数对重建声场进行信息补偿.数值算例结果表明：补偿信息后的射线波函数不仅保证了声场重建过程中数值计算的稳定性，而且弥补了单一射线波函数在低波数处的缺陷，进一步提高了声场的重建精度.

关键词：近场声全息;波叠加法;射线波函数;信息补偿 ;声场重建

中图分类号：TB52            DOI：10.16375/j.cnki.cn45-1395/t.2021.03.002

0    引言

基于波叠加法的近场声全息理论[1-2]因其算法简单、计算效率较高，被广泛应用于声源识别、定位和声场重建，其基本思想是：声源产生的声场可由该声源内部一系列虚拟等效源产生的声场叠加替代，而虚拟等效源的源强可以通过匹配全息面的测量声学信息得到[3].波叠加法一般采用的是只与距离有关的球形单极子函数，其构成的系统矩阵通常为一病态矩阵，影响了数值计算的稳定性.对于弱病态的系统矩阵，通常采用正则化方法[4-5]过滤或截断较小奇异值来抑制测量误差的影响，提高数值计算的稳定性.为了获取更高的计算精度，贺春东等[6-8]对近场声全息的正则化方法作了进一步的优化.然而，单一的正则化方法无法从根本上改变系统矩阵的固有缺陷，要确保重建结果与实际声场信息相吻合，有时还需要对等效源的位置作进一步选择[9]和优化[10-11].无论何种优化方式，计算过程中都是通过改变系统矩阵形态来对重建结果施加影响.Song等[12]对系统矩阵研究后指出，要获得较高的计算精度，系统矩阵需满足对角占优且尽量对称.

为了使系统矩阵满足上述条件，文献[13]提出以格林函数的[n（n=1， 2， 3， …）]阶方向导数为积分核函数的射线波叠加法.与传统波叠加法相比，射线波叠加法有效地改善了系统矩阵的病态性，并获得了较为稳定的计算结果.但是，射线波叠加法在低波数处声场重建效果并不理想.其原因在于射线波函数在低波数处的指向性过强，其叠加声场信息将主要集中在各个射线波等效源的主指向处，而在非主指向处出现了信息缺失.

为了克服以上问题，本文在射线波函数中添加一定权重的球形单极子函数来弥补声场缺失的信息.研究发现，经过信息补偿后的射线波函数不仅保证了系统矩阵趋于良态，而且提高了声场的重建精度.最后通过脉动球声源以及双脉动球干涉声源验证了本文方法的优越性.

1    波叠加法及射线波函数的性质分析

将虚拟等效源布置在辐射声源内部的封闭曲面[SE]上，可得辐射体外部区域任意一点声压[p（r）][3]：

[pr=SEqrEgr，rEdSE]              （1）

其中：[q（rE）]为待求等效虚拟源强，[g（r，rE）=eikR/（4πR）]，[i=-1]，[k]为波数，[R=r-rE].若将等效源面[SE]网格离散成N个节点，同时在节点处配置[N]个单极子声源，得到离散后的积分方程：

[p（r）=i=1Nq（rEi）g（r，rEi）]               （2）

由式（2）可知，声源外部的辐射声场可由内部一系列虚拟声源辐射声场叠加得到.若全息面上存在[N]个全息测点，可将式（2）转化为矩阵形式如下：

[PH=GHQ]                           （3）

式中：[PH]为测点声压列向量，[GH]为全息面测点与等效源之间的系统矩阵，[Q]为待求等效源源强向量.通过对[GH]求逆即可计算得到[N]个虚拟等效源的源强，然后将求得的源强代入式（2）即可求解声源面外部任意位置的声压[p（r）].但由于格林函数[g（r，rE）]是一个球波函数，其构成的系统矩阵[GH]往往是一个病态矩阵，数值求逆时会放大测量误差的影响，可能导致重建结果失真.为了克服以上问题，文献[13]构造了具有主指向的射线波函数来替代传统波叠加法的单极子球波函数，极大地提高了声场重建的数值稳定性.

2    射线波函数的特点及缺陷

Ochmann[14-15]指出只要满足Helmholtz方程和Sommerfield辐射条件的解析函数均可以作为波叠加法的积分核函数.基于这一研究思路，可以通过改变积分核函数的方式提高声场重建的数值稳定性[16-17].在文献[13]中构造了如下的射线波函数：

[Ki（r，rE）=?（i）g（r，rE）?l（i），i=1，2，3，…]      （4）

式中：[Ki（r，rE）]为具有指向性的射线波函数，[l]为其主指向，[i]为求导阶数.当[i=1]且[l]为等效源面法向量n时，[?g（r，rE）?n]为常用的双层势函数.经过计算发现，随着求导阶数的增加，射线波函数的指向性逐渐增强，如图1所示.

若将上述的N个射线波等效源的主指向与全息面测点一一对应，系统矩阵如下：

[Ki（r，rE）=Ki（r1，rE1）Ki（r1，rE2）…Ki（r1，rEn）Ki（r2，rE1）Ki（r2，rE2）…Ki（r2，rEn）???Ki（rN，rE1）Ki（rN，rE2）…Ki（rN，rEn）N×N]（5）

由于在[rEi]处的射线波等效源在其对应的全息测点[ri]处的声波激励最大，其构成的系统矩阵[Ki（r，rE）]呈现主对角占优且近似对称.与传统单极子等效源构成的系统矩阵相比，[Ki（r，rE）]具有较好的数值稳定性，不会因为很小的测量误差导致计算结果失真[12].

经过进一步的研究发现，当射线波函数指向性过强时，系统矩阵会出现以下情况：

[Ki（rn，rEn）?Ki（rn，rEm），n， m=1， 2， 3， …且 m≠n]   （6）

即系统矩阵主对角元素远大于非主对角元素，此时尽管系统矩阵的数值稳定性较好，但重建声场与实际声场信息不匹配.原因如图2所示.

指向性过强的射线波等效源辐射的声场信息主要集中于与之对应的全息面测点附近，而在远离全息面测点的位置将会出现信息缺失.因此，选取的射线波求导阶数不宜过高，一般为2～3阶.其次，文献[13]的数值算例指出，射线波函数的重建效果与波数也有一定的关系，其在低波数处重建效果不太理想.经分析发现，如图3所示，在相同的求导阶数下，射线波函数在低波数处的指向性较强，而在波数较大时，指向性强度相对较弱.说明了波数较小时，由于射线波等效源的指向性过强，导致了声场重建信息缺失.

3    射线波函数的信息补偿

由于在低波数处射线波函数的声场信息主要集中在各个射线波的主指向性处，导致其他位置的声场信息缺失，因此，需要采用一定的策略对缺失的声场信息进行补偿.单极子球面波函数是一种全空间覆盖且在各个方向均匀衰减的波函数，因此，本文考虑在射线波函数中添加一定权重的单极子波函数对声场信息进行补偿，表达式如下：

[K（i）a（r，rE）=ag（r，rE）+?（i）g（r，rE）?l（i），i=0， 1， 2， 3，…]（7）

其中：i为求导阶数，[a]为组合权重系数.通过选取合适的权重系数就可以保证射线波函数构成的系统矩阵趋于良态的同时，提高低波数处声场的重建精度.为了便于对比，给出不同权重系数时的射线波函数[K（3）a（r，rE）]指向性，如图4所示.

由图4可以看出随着单极子波函数权重的增加，射线波函数的指向性逐渐减弱，因此，可以通过调整参数[a]的大小，补偿合适的球面波信息，在保证改善低波数处声场重建精度的同时，提高声场重建的数值稳定性.

4    数值算例与分析

为了验证加入单极子球波函数后射线波函数的数值稳定性以及对低波数处的改善效果，选取文献[13]中数值计算稳定较好的三阶射线波函数[?（3）g（r，rE）?l（3）]进行组合对比验证，其中重建声源模型为脉动球声源和双脉动球干涉声源.

4.1   脉动球声源重建效果对比

首先采用脉动球声源进行验证，半径为[Rs]的脉动球声源在距离圆心为[r]处声压如下[18]：

[p（r）ρ0cv0=RsrikRs1+ikRse-ik（r-Rs）]            （8）

其中：[ρ0]为介质的平均密度，[v0]为脉动球表面质点法向振速幅值，[c]为声波在介质中的传播速度，[i=-1]，  [k]为波数.设定[ρ0=1.21] [kg/m?]，[v0=1] [m/s]，[c=340] [m/s].脉动球声源半径[Rs]=1.0 m.全息面半径为1.5 m的球面，按照纬度间隔[π/11]，经度间隔[2π/11]布置全息测点，除去两极，共100个节点.等效源面半径    [rE=0.2] [m]，其等效源点经纬度分布方式与全息测点  相同.

根据上述模型布置，分别采用常用的单极子波函数[g（r，rE）]、双层势波函数[?g（r，rE）?n]、三阶射线波函数[?（3）g（r，rE）?l（3）]以及信息补偿后的射线波函数[K（3）a（r，rE）]进行声场重建，其中经过大量算例验证[a=1～10]时系统矩阵较为稳定，而且改善效果较为明显.本文选取[a=8].在数值计算中，系统矩阵条件数大小可以衡量矩阵的病态程度，所以首先对比在不同波数下各个波函数构成的系统矩阵条件数如图5所示.

图5表明，單极子波函数构成的系统矩阵条件数较大，采用双层势波函数[?g（r，rE）?n]可以降低系统矩阵条件数，而采用三阶射线波函数[?（3）g（r，rE）?l（3）]和[K（3）a（r，rE）]降低效果更加明显，说明射线波函数和组合后的射线波函数均能够有效改善系统矩阵的病态性，提高声场计算的数值稳定性.

为了验证以上各个波函数在不同波数的重建精度和稳定性，在全息测点声压中添加40 dB的噪声，并利用以上各个波函数对脉动球表面声压实部和虚部进行重建.不同波函数的重建效果如图6所示.

图6（a）可以看出，单极子波函数[g（r，rE）]重建数值解完全偏离了解析解，图6（b）中双层势波函数[?g（r，rE）?n]的重建效果有所改善，但是部分波数处吻合程度较差;采用三阶射线波函数[?（3）g（r，rE）?l（3）]在低波数处重建数值解偏离了解析解，在波数较大时重建效果较好;信息补偿后的射线波函数[K（3）8（r，rE）]在各个波数处均有较好的重建效果.综合条件数对比和重建结果来看，补偿信息后的射线波函数既改善了系统矩阵的病态性，又弥补了单一射线波函数在低波数处的缺陷.

4.2   雙脉动球干涉声源节点声压重建

在实际工程中，声场的分布通常较为复杂且无解析解可循.本文根据替代法[19]的原理，利用双脉动球形成的干涉声场代替实际声场，其中2个脉动球中心坐标分别为（0.2， 0， 0）和（-0.2， 0， 0），半径均为0.4 m，振速为[v=1] [m/s].全息面为半径[RH=1.0] m的球形，节点分布纬度间隔为[π12]，经度间隔为[2π12]，除去两极节点，共121个节点.等效源布置面半径为[r=0.2] m，等效源点分布与全息测点相同.声场重建节点均匀分布在一半径为0.8 m的圆形之上，共121个重建节点.其二维示意图如图7     所示.

依旧采用上述单极子波函数[g（r，rE）]、双层势波函数[?g（r，rE）?n]、三阶射线波函数[?（3）g（r，rE）?l（3）]以及信息补偿后的射线波函数[K（3）8（r，rE）]对声场进行重建.为了验证补偿后射线波函数在低波数处的改善效果，设定波数为[k=0.5]，并对全息测点声压数据添加40 dB的噪声.对比重建节点解析解声压以及重建数值解声压如图8所示.

根据图8可以看出单极子波函数[g（r，rE）]、双层势波函数[?g（r，rE）?n]、三阶射线波函数[?（3）g（r，rE）?l（3）]在各个节点的重建声压均偏离了解析解，而补偿信息后的射线波函数[K（3）8（r，rE）]在节点处重建结果与解析解的吻合程度较好，说明低波数处补偿信息后的射线波函数在空间不同位置处均有较好的重建效果.根据表1中各个系统矩阵条件数对比可以发现，单极子波函数[g（r，rE）]和双层势波函数[?g（r，rE）?n]由于条件数较大，在利用MATLAB计算过程中已经出现提示求逆计算结果可能不准确.而相比单极子波函数[g（r，rE）]和双层势波函数[?g（r，rE）?n]，虽然三阶射线波函数[?（3）g（r，rE）?l（3）]条件数最小，但是重建效果依旧不太理想，结合射线波函数缺陷的分析，说明在低波数处利用射线波函数[?（3）g（r，rE）?l（3）]重建声场时出现了信息缺失.而补偿信息后的射线波函数[K（3）8（r，rE）]不仅降低了系统矩阵条件数，改善了系统矩阵的病态性，而且保证各个节点处声场的重建精度，因此，足以说明本文方法的优越性.

5    结论

本文综合考虑了系统矩阵以及各个波函数的特性，提出了一种射线波函数信息补偿法，即在射线波函数中添加一定权重的单极子球波函数对声场信息进行补偿.数值算例结果表明：信息补偿后的射线波函数显著降低了系统矩阵的条件数，既保证了声场重建的数值稳定性，又弥补了单一射线波函数在低波数的缺陷，提高了声场重建的计算精度.在实际工程应用当中，结构体振动辐射的声场更加复杂，经验性地选取组合参数可能无法满足重建精度的要求，因此，如何稳定选取最优的组合参数使射线波函数能够适应于任意声场的重建是下一步的研究重点.

参考文献

[1]   KOOPMANN G H，SONG L M，FAHNLINE J B.A method for computing acoustic fields based on the principle of wave superposition[J].The Journal of the Acoustical Society of America，1989，86（6）：2433-2438.

[2]    LEE S. Review：the use of equivalent source method in computational acoustics[J].The Journal of Computational Acoustics，2017，25（1）：1630001.

[3]   JEANS R，MATHEWS I C.The wave superposition method as a robust technique for computing acoustic fields[J].The Journal of the Acoustical Society of America，1992，92（2）：1156-1166.

[4]   WILLIAMS E G.Regularization methods for near-field acoustical holography[J].The Journal of the Acoustical Society of America，2001，110（4）：1976-1988.

[5]    陈达亮， 舒歌群， 卫海桥. 近场声全息正则化方法比较[J]. 天津大学学报， 2008，41（6）： 696-702.

[6]    贺春东， 张永斌， 毕传兴，等. 分部优化正则化在近场声全息技术中的应用[J]. 声学学报， 2011，36（4）： 419-426.

[7]   CHELLIAH K，RAMAN G G，MUEHLEISEN R T. Enhanced nearfield acoustic holography for larger distances of reconstructions using fixed parameter Tikhonov regularization[J].The Journal of the Acoustical Society of America，2016，140（1）：114-120.

[8]    XIAO Y. A new method for determining optimal regularization parameter in near-field acoustic holography[J].Shock and Vibration，2018，2018： 1-13.

[9]    BAI M R，CHEN C C，LIN J H.On optimal retreat distance for the equivalent source method-based nearfield acoustical holography[J].The Journal of the Acoustical Society of America，2011，129（3）：1407-1416.

[10] WU S W，XIANG Y.Location optimization of monopole equivalent sources in wave superposition method[J].International Journal of Acoustics and Vibration，2018，23（2）：254-263.

[11]   GOUNOT Y J R，MUSAFIR R E.Genetic algorithms：a global search tool to find optimal equivalent source sets[J].Journal of Sound and Vibration，2009，322（1-2）：282-298.

[12]   SONG L M，KOOPMANN G H，FAHNLINE J B. Numerical errors associated with the method of superposition for computing acoustic field[J].The Journal of the Acoustical Society of America，1991，89（6）：2625-2633.

[13]   向宇，石梓玉，陆静，等.基于波叠加法的非共形近场声全息波函数的构造与选择[J].振动与冲击，2020，39（15）：183-192.

[14]   OCHMANN M A.The source simulation technique for acoustic radiation problems[J].Acta Acustica united with Acustica，1995，81（6）：512-527.

[15]   OCHMANN M A.The full-field equations for acoustic  radiation and scattering[J].Journal of the Acoustical Society of America，1999，105（5）：2574-2584.

[16]   石梓玉，向宇，陆静，等.一种提高声场重构稳定性的射线等效源法[J].广西科技大学学报，2019，30（3）：1-7，21.

[17]   张阳，向宇，石梓玉.二维声全息的δ函数约束型射线波叠加法[J].广西科技大学学报，2020，31（4）：19-26，48.

[18]   CHIEN C C，RAJIYAH H，ATLURI S N.An effective method for solving the hyper-singular integral equations in 3-D acoustics[J].The Journal of the Acoustical Society of  America，1998，88（2）：918-937.

[19]  KIRKUP S M，HENWOOD D J.Methods for speeding up the boundary element solution of acoustic radiation problems[J].Journal of Vibration and Acoustics，1992，114（3）：374-380.

Information compensation of ray wave function based on wave

superposition near field acoustic holography

CHEN Yanhao1，2，XIANG Yu*2，SHI Ziyu2

（1.School of Mechanical and Traffic Engineering， Guangxi University of Science and Technology，

Liuzhou 545006， China; 2.Guangxi Key Laboratory of Automobile Component and Vehicle Technology （Guangxi University of Science and Technology）， Liuzhou 545006， China）

Abstract： Near field acoustic holography based on wave superposition has been widely used in sound source identification， location and field analysis in recent years because of its advantages in adaptability and numerical calculation. In the near-field acoustic holography technology based on the wave            superposition method， the ray wave function as the integral kernel function of the wave superposition method can effectively improve the ill-conditionedness of the system matrix and improve the numerical stability of the sound field calculation. However， due to the strong directivity of the ray wave function at low wave numbers， the sound field information is mainly concentrated at the main direction of the ray wave function， resulting in the lack of sound field information in other directions. To solve the above problems， a ray wave function information compensation method is proposed， that is， a certain proportion of monopole spherical wave function is added to the ray wave function to compensate the  reconstructed sound field. Numerical example results show that the ray wave function after               supplementary information not only guarantees the stability of the numerical calculation in the sound field reconstruction process， but also makes up for the defect of a single ray wave function at low     wavenumbers， and further improves the accuracy of sound field reconstruction.

Key words： near-field acoustic holography; wave superposition method; ray wave function; information compensation; sound field reconstruction.

（責任编辑：黎  娅）