井下段钻柱耦合振动及钻井液压力分析*
2021-07-12杜青云
刘 静 王 川 郝 晨 杜青云 王 涛 张 铖
(1.西南石油大学机电工程学院 2.大港油田石油工程研究院3.中国石油集团渤海钻探工程有限公司定向井技术服务分公司)
0 引 言
在深水钻井作业过程中,当钻头与地层接触时,钻柱系统会同时受到横向、纵向和扭转振动的干扰,这严重影响钻柱和井下设备的使用寿命。产生这些振动的原因包括井筒内壁和钻柱以及钻头和地层界面的冲击和摩擦、钻铤段的不平衡、偏心或初始曲率、各种线性或非线性共振等。这些振动通常比较复杂,并且同时发生[1-2]。R.DAWSON等[3]和牟海维等[4]系统研究了钻柱的黏滑振动,并证明只能用非线性摩擦力解释黏滑现象。况雨春等[5]建立了钻头和钻柱扭转振动仿真模型,得到了钻头处扭矩的变化规律,但没有考虑波动钻速对扭矩的影响。W.R.TUCKER等[6]建立了一个完整的连续介质模型,该模型解释了横向、纵向和扭转振动之间的完全耦合以及它们之间的能量交换,但没有考虑井筒压力的变化。刘清友等[7]将井下部分的钻柱和钻头简化为弹簧-阻尼-质量系统,建立了钻头和岩石相互作用的动力学模型,钻头和钻柱横向、纵向和扭转振动模型,但没有分析不同振动方式的耦合作用。韩春杰和闫铁等[8-10]采用微元线性法对钻柱的横向、纵向和扭转振动进行了分析,使用有限元法研究了钻柱轴向的振动规律,但没有分析钻井参数对钻压的影响。李国庆等[11]使用有限元方法分析了钻柱的横向、纵向和扭转耦合振动,在考虑钻柱耦合振动的弹性刚度和几何刚度基础上,建立了钻柱耦合振动分析的综合模型,但是没有分析井筒内钻井液的压力波动情况。
针对上述问题,本文通过对深水钻井井下段钻柱的受力分析,建立了井下段钻柱非线性耦合振动数学模型和井筒内钻井液压力波动模型,分析了波动钻压对钻柱横向和纵向耦合振动以及井筒内钻井液压力波动的影响,以及波动转速对钻柱纵扭耦合振动、黏滑振动、钻压以及钻头扭矩的影响。
1 钻柱非线性耦合振动数学模型
深水钻井过程中地层的不确定性会使钻头受力不稳定,容易引起跳钻以及钻头扭矩波动。钻头主动扭矩的释放会导致钻柱发生周期性反转,加剧钻柱纵向振动[12]。钻柱扭转振动时会发生横向变形,与井壁接触产生摩擦。摩擦力会引起钻柱涡动和黏滑振动,同时加剧钻柱反转,反过来影响钻柱横向和纵向振动,几种振动耦合在一起产生的交变应力极易使钻柱发生断裂和磨损等事故。钻柱耦合动力学除了与钻柱和井眼参数有关外,还与环境和钻井平台等因素有关,合理分析深水钻井钻柱耦合动力学机理对减少钻具疲劳失效至关重要。井下段钻柱耦合振动模型如图1所示。

图1 井下段钻柱耦合振动模型
钻柱在井筒内的3个自由度分别为轴向位移z、横向位移r和旋转角度θ。设井眼轴线与井口平面的交点为坐标系原点,钻柱轴向位移竖直向下的方向为正,横向位移指向井壁的方向为正,钻柱绕井眼中心轴的旋转角度以逆时针方向为正。在切削钻进过程中,钻柱系统的转速Φr以及预设钻压(Wob)由顶部钻机提供。
1.1 基本假设
钻柱的横向、纵向和扭转振动通常同时存在,并且互相影响。为了研究钻柱的非线性耦合振动规律以及钻柱振动对钻压、转速和钻井液压力的影响,取从井口到井底的钻柱整体为研究对象,并在以下假设的基础上搭建钻柱非线性耦合振动模型:①钻柱结构一体化,将其视为弹性体;②对于纵向振动,将钻柱两端简化为铰支,不考虑钻柱接头处与井壁的接触外力,只考虑受力变形;③钻柱截面为圆形,其内外边界以及井筒内壁都为刚性;④井口为固定端,井筒底部为自由端;⑤钻柱轴线与井眼轴线重合,且转角为0。
1.2 非线性耦合振动方程
在上述假设的基础上,参考文献[13]建立井下段钻柱非线性耦合振动微分方程:
(1)
式中:ml、ma分别表示钻柱系统横向和轴向有效质量,Fr、Ft分别表示钻柱与井壁接触时产生的径向力和切向力,Fob和Tob分别表示钻柱对井底的压力以及钻头受到的扭矩,ka、kr、kt分别表示钻柱纵向、横向和扭转刚度,ch、ca、ct分别表示井筒内钻井液对钻柱横向、纵向以及扭转振动损耗系数,v表示钻柱中心在水平方向上的速度,eo表示钻柱的偏心率,J表示钻柱的转动惯量,Dco表示钻铤外径。
上述方程中的变量Fob和Tob可以用如下非光滑方程进行描述[14-15]:
(2)
(3)
式中:kc表示地层刚度,so表示钻井不规则参数,Dw表示井眼直径,nb表示钻头系数,与钻头类型相关。
钻头上的扭矩由钻头与井壁的摩擦力以及钻头切削岩石的力共同抵消,摩擦损耗部分由以下平滑函数给出:
(4)
式中:us为钻头与井壁的静摩擦因数,uk为钻头与井壁的动摩擦因数。
δc表示钻头的平均切削深度,表达式为:
(5)

(6)
钻柱与井筒的接触力可分解为沿径向的力Fr和垂直于径向的切向力Ft两种非光滑力,其定义如下:
(7)
(8)
式中:Dw表示井眼直径;横向接触力f(vrel)通过参考文献[13]提出的轴向扭转接触来描述,其表达式为:
(9)

(10)
考虑钻井液对钻柱系统有效质量的影响,钻柱系统在纵向和横向上的有效质量ma、ml可分别表示如式(11)和式(12)所示。同时为了简化模型,底部钻具组合只考虑钻铤。
ma=mBHA+mad+mdp
(11)
ml=mBHA+mad
(12)
式中:mBHA表示底部钻铤的质量,mad表示钻井液对钻铤的附加质量,mdp表示钻柱质量。
钻柱系统的扭转惯量J由钻柱底部钻具组合惯性和上部钻柱惯性组成,其表达式如下:
(13)
式中:ρ表示钻柱材料密度,dco表示底部钻铤的内径,lBHA表示钻铤长度,Ddp和ddp分别表示钻柱的外径和内径,ldp表示钻柱长度。
钻柱在纵向、横向和扭转方向上的刚度计算方法如下。其中,横向刚度kr受钻头扭矩和钻压的影响,表明钻柱的横向刚度会随着钻头的扭矩和钻柱对井底的压力波动而发生变化。
(14)
(15)
(16)
式中:E和G分别表示弹性模量和剪切模量,I表示钻柱的惯性矩,其计算式如下。
(17)
2 钻柱振动引起的压力波动
2.1 钻柱升沉运动引起的压力波动
(18)
式中:ΔpG表示因钻柱升沉运动引起的井眼环空内压力波动,ΔS=x(t),表示钻柱底部升沉运动的位移,Vd表示井眼内钻柱的体积,Va表示井眼内钻井液的体积,cf表示井眼内钻井液的可压缩性系数。
2.2 钻柱弯曲变形引起的压力波动
钻柱在井筒内的横向、扭转振动以及钻具的涡动都会引起钻柱的弯曲变形,考虑由于钻柱的弯曲变形引起的钻井液的流动,则其造成的流体压力分布为[17]:
(19)
(20)
(21)
式中:Ω和ω分别表示钻柱转动和涡动角速度,h表示井眼轴线到钻柱外缘一固定点的距离。
3 模型求解及模拟分析
采用四阶龙格-库塔方法在Matlab中搭建模型,进而求解钻柱耦合振动模型。龙格-库塔法是解微分方程的方法之一,由于其精度高、收敛稳定,所以在工程上应用十分广泛。其表达式如下:
(22)
其中:
k1=f(xn,yn)
(23)
(24)
(25)
k4=f(xn+h,yn+hk3)
(26)
将耦合模型降阶后可表示为:
(27)
由式(23)~式(26)可以得出耦合模型的龙格-库塔求解公式:
(28)
其中:
(29)
(30)
(31)
(32)
在建立深水钻井井下段钻柱耦合振动模型时,主要考虑了钻井系统的钻压和转速等因素对钻柱耦合振动以及井筒内钻井液压力的影响。以南海某深水井数据为例,其水深1 000 m,井深500 m,钻柱和钻铤长度分别为1 300和200 m,钻柱内、外径分别为0.135 8和0.168 3 m,钻铤内、外径分别为0.076 2和0.228 6 m,钻柱材料密度为7 850 kg/m3,其弹性模量和剪切模量分别为210和78 GPa。钻井液密度为1 300 kg/m3,且假设其不可压缩,井筒内钻井液的附加质量为33 450 kg。井眼直径为0.381 m,地层刚度为23 000 kN/m,钻井不规则参数s0=0.001。顶部钻机的额定转速为40 r/min,平均钻压为22.5 kN。钻柱的损耗系数ch、ca、ct分别为21 830、4 000、7.4,钻柱与井壁的动摩擦因数为0.3、静摩擦因数为0.35。钻柱的偏心率eo=0.5,钻头系数nb=3。基于上述参数,对井下段钻柱的各种耦合振动进行模拟分析。
3.1 深水钻井钻柱横纵耦合振动分析
深水钻井中,井下段钻柱的横向振动主要由中性点至钻头段产生的离心力引起,离心力会使钻柱弯曲变形,从而导致其纵向应力变化。钻柱的纵向振动导致底部钻压变化,反过来影响钻柱受到的轴向力,从而影响钻柱的横向振动和井筒钻井液压力分布。不同钻压下钻柱的横向、纵向振动规律以及井筒内钻井液压力波动规律如图2~图6所示。

图2 不同钻压下钻柱的横向振动响应
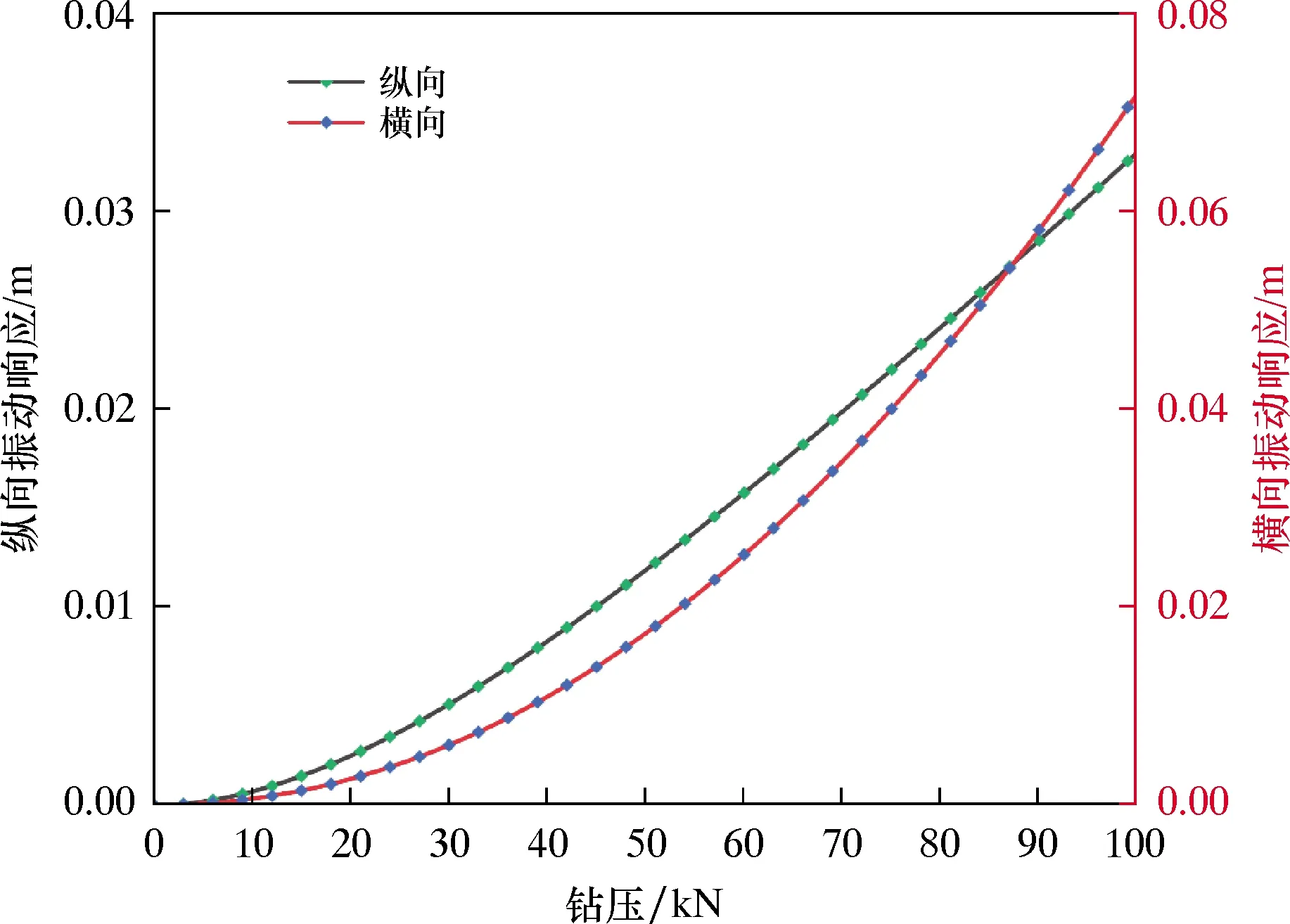
图3 钻柱横向和纵向振动响应随钻压的变化

图4 中性点横向振动响应和井筒压力波动

图5 不同钻压下钻柱纵向振动响应

图6 不同钻压下井底钻井液压力波动
由图2和图3 可以看出,在仅考虑钻压的情况下,井下段钻柱的横纵向振动响应随钻压的增加而变大,钻压对钻柱的横向振动影响更为明显。这是由于钻压会影响地层对钻柱系统的轴向支撑力,从而导致钻柱横向振动频率改变。图4表明井下段钻柱中性点的横向振动响应和附近的钻井液压力也随钻压的增加而变大,同时呈周期性变化。由图5和图6可以看出,井下段钻柱的纵向振动响应随时间呈周期性变化,受到钻柱纵向振动的影响,井底钻井液压力也随时间呈周期性变化,同时钻井液压力随钻柱纵向振动幅度的增大而上升。
3.2 深水钻井钻柱纵扭耦合振动
深水钻井中,井下段钻柱的旋转运动会引起纵向振动和动载,底部钻具的纵向振动导致钻压和井底压力波动。由于钻压的剧烈波动,钻头脱离井底引起跳钻,跳钻会对钻头造成冲击。钻头黏滑振动引起的钻头转速波动会加剧钻柱纵向振动。此外,钻柱纵向运动导致的周期性反转运动也会加剧钻头上的扭矩波动,从而影响黏滑振动。
不同转速下的钻压波动和钻头黏滑振动分别如图7和图8所示。钻头与地层保持接触时,钻压不为0。当钻头发生黏滑振动时,储存在钻柱中的能量会被释放,从而导致非常大的纵向和扭转振动。纵向振动反过来又影响钻压和钻头扭矩的大小。当转速增加时,钻柱的纵向振动幅度以及钻头扭转振动幅度都会增大,这是因为纵向共振的作用。这种共振导致钻头与地层失去接触,钻压和钻头扭矩都为0。由图9和图10可以看出,随转速的增大,虽然钻柱的纵向振动和钻头扭矩波动也随之增大,但转速增大对钻柱纵向振动影响更大。此外,钻头处的扭矩波动随时间呈现周期性变化。因此,在进行钻井作业时,需要根据不同的工作环境选择合适的转速。
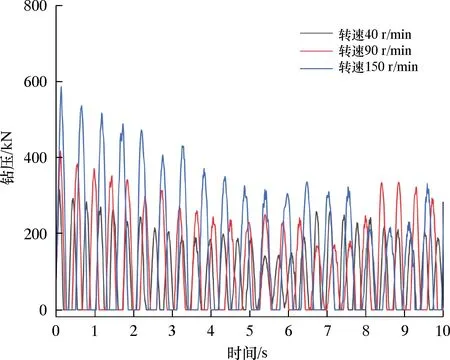
图7 不同转速下的钻压波动

图8 不同转速下钻头黏滑振动

图9 钻柱纵向振动和钻头扭矩随转速的变化

图10 不同转速下钻头扭矩波动
4 结 论
(1)针对深水钻井作业中井下段钻柱横向、纵向和扭转方向的非线性耦合振动以及井筒内钻井液压力波动的问题,建立了井下段钻柱横向、纵向、扭转耦合振动和钻井液压力波动的数学模型,通过对各种钻井情况下钻井系统的钻压和转速等参数的模拟计算,获得了井下段钻柱耦合振动的基本规律以及钻井液压力波动规律。
(2)增大钻压对钻柱的横向振动影响最大,同时又导致了井筒内钻井液压力的剧烈波动,使钻柱动力稳定性变差。
(3)增大转盘转速对钻柱系统纵向振动影响最大,转速的增大会使钻柱的纵向振动幅度和钻头扭矩波动幅度上升,降低钻柱稳定性。
(4)钻柱系统的耦合振动存在共振的可能,并且耦合振动呈一定的周期性变化。钻柱耦合振动规律的深入研究有助于钻柱振动理论及分析方法的完善,并且对工程施工具有一定的指导意义。
