基于阶跃激励稳态响应的感应电机匝间短路故障诊断方法研究
2021-07-12刘赫雷雨秋张心怡李志远周玮
刘赫,雷雨秋,张心怡,李志远,周玮
(1.中国电力科学研究院有限公司,北京 100192;2.国网杭州供电公司,浙江杭州 310000)
近年来,随着电力设备的数字化、智能化发展,交流电机的状态监测技术得到了研究人员的广泛关注[1-5]。工业领域的调研显示,在所有已发生的故障当中,感应电机定子故障占比达到约37%,而其中高达90%的故障与绕组有关[6]。作为机械、电气层面均十分脆弱的电机重要组件,定子绕组的故障初期通常被描述为匝与匝之间的短路异常状态。如果初期的匝间短路没有被及时发现,那么将会导致极为严重的相间、相地短路,最终烧毁电机,而且还会对电源侧产生极大危害[7]。因此,开展感应电机定子匝间短路故障诊断具有重要的实际意义。
目前,研究人员已经提出了多种诊断及检测方法,其中负序电流分量法及电流特征频率法属于传统的交流电机检测方法[8-9]。此类方法原本应用于工业中电网直接驱动电机的定子状态监测,而后被引入各类现代控制驱动系统当中[10]。然而,为了实现电流的数据采集、频谱分析以及特征提取,需要电机保持长时间的稳态运行。但是,在包括电力装备电机操动机构、弹簧装置电机储能机构等在内的应用场景下,调速电机通常处于短时非稳态、变负载的工作状态,并不满足传统方案的实现条件。
基于逆变器自身特点的高频注入法最早被应用于电机的参数辨识,近年来被引入交流电机定子故障诊断研究[11-12]。此类方法能够避免基波、谐波等信号受电机运行状态制约的问题,而且可以在静止的间隙时间开展检测。但是,额外的注入高频不但增加了系统的损耗,还会恶化工业现场的电磁环境。另外,部分功率型低载波比驱动系统实际上并不具备高频注入的能力。
针对上述问题,提出了一种基于阶跃激励稳态响应的感应电机匝间短路故障诊断方法,并开展了理论与实验分析。该方法在电机静止情况下,利用驱动器在线输出等效单相激励,通过分析电机三相电流的稳态响应,以实现定子匝间短路的故障诊断。研究过程中开展了单相激励下故障电机电流的解析分析,给出了包含故障信息的特征矢量,提出了故障指标的计算表达式,相关实验结果验证了提出方法的有效性与可靠性。
1 理论分析
图1 给出了故障电机的单相激励连接方式,仅考虑如图所示的初期匝间短路故障类型。认为故障发生于A相,可以列出如下2 种状态:1)通路匝间短路;2)支路匝间短路。根据单相T型等效电路可知,转子侧仅包含转子电阻与转子漏感2项,且定子故障不会改变转子侧结构,因而依据叠加原理,在分析过程中暂时忽略转子侧的影响[13-14]。

图1 包含匝间短路的感应电机单相激励连接图Fig.1 Diagram for single-phase test of induction machine with ITSC
1.1 通路匝间短路
图2为通路匝间短路等效电路。

图2 通路匝间短路等效电路Fig.2 Equivalent circuit of windings with the ITSC in main path
考虑如图2 所示的电路结构,由网格法可以得到如下方程:
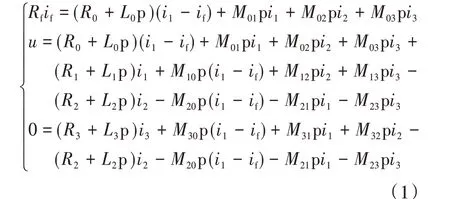
式中:R为电阻;L为自感;M为互感;i为电流;u为电压;p为微分算子;下标f表示短路回路参量;下标0~3分别对应图中各部分电机绕组的电气参量。
根据绕组函数法,可以得到式(1)中各变量的解析表达式:

式中:Rs为定子电阻;Lls为定子漏感;Lms为定子励磁电感;μ为相绕组的短路匝数比例。
求解式(1)可以得到如下以A相电流i1与短路电流if为变量的微分方程组及其对应变量的表达式:
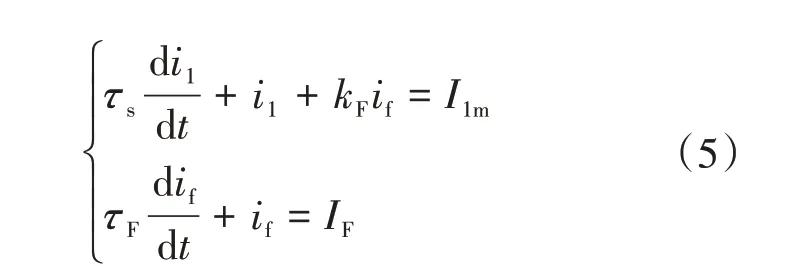
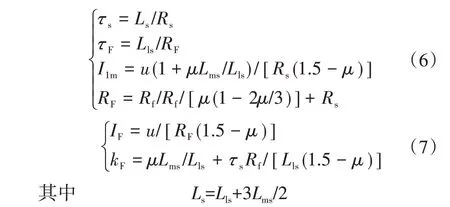
式中:τs为定子时间常数;τF为短路时间常数;I1m为A相作为通路情况下的定子电流激励;IF为故障电流激励;RF为等效短路电阻;kF为等效短路系数;Ls为定子电感。
由于电感Ls明显大于漏感Lls,且由式(6)中RF的定义可知,故障初期根据等效短路电阻RF不小于定子电阻Rs,从而可以认为式(6)中τs远大于τF。因此,独立求解式(5)中第2 行,可以得到足够长时间后的故障电流零状态响应:
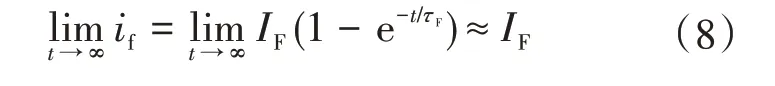
将式(8)结果代回式(5)中第1 行,可以得到A相电流的近似零状态响应,同时根据对称性可以直接得到支路电流的解析表达式。综上,通路中发生匝间短路时,电机电流的求解结果为
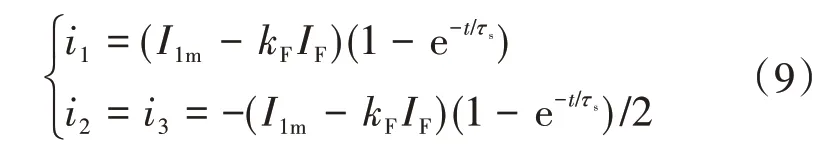
1.2 支路匝间短路
图3为支路匝间短路等效电路。

图3 支路匝间短路等效电路Fig.3 Equivalent circuit of windings with the ITSC in branch path
改换激励的连接方式,考虑如图3 所示的电路结构,能够得到如下方程:
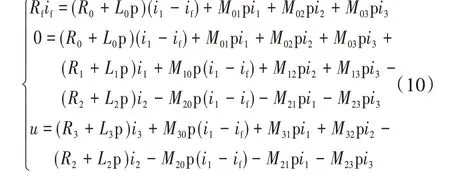
求解式(10)可以得到以C相电流i3与短路电流if为变量的微分方程组,以及对应变量的解析表达式:
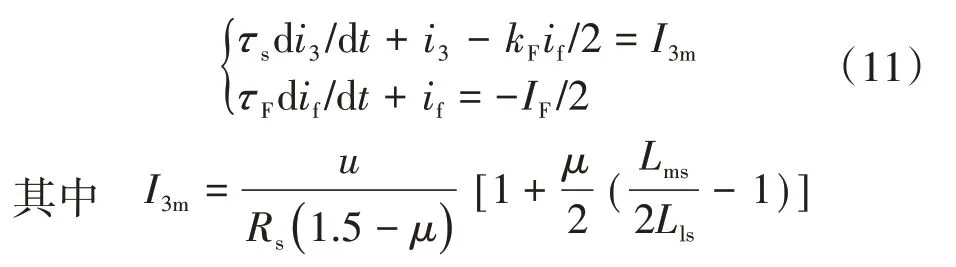
式中:I3m为C相作为通路情况下的定子电流激励。
同理,由式(11)中第2 行可以得到故障电流近似式,代回第1 行即可实现C相电流的近似求解。考虑到支路匝间短路状态下,两支路并不呈现对称的特征,因此利用式(10)与相电流之和为零的关系重新计算支路电流。综上,支路中发生匝间短路时,电机电流的求解结果为
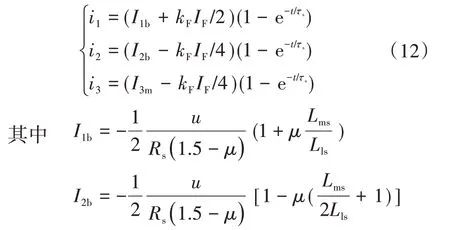
式中:I1b,I2b分别为A相、B相作为支路情况下的定子电流激励。
2 诊断方法
2.1 支路等效环流
利用式(9)和式(12)可以计算得电机通路及支路中分别发生故障时,电流稳态响应数值随短路电阻与短路比例的变化曲线。图4、图5 给出了对应的曲线结果,计算参数为:Rs=9.06 Ω,Lls=23 mH,Lms=379 mH,u=15 V。
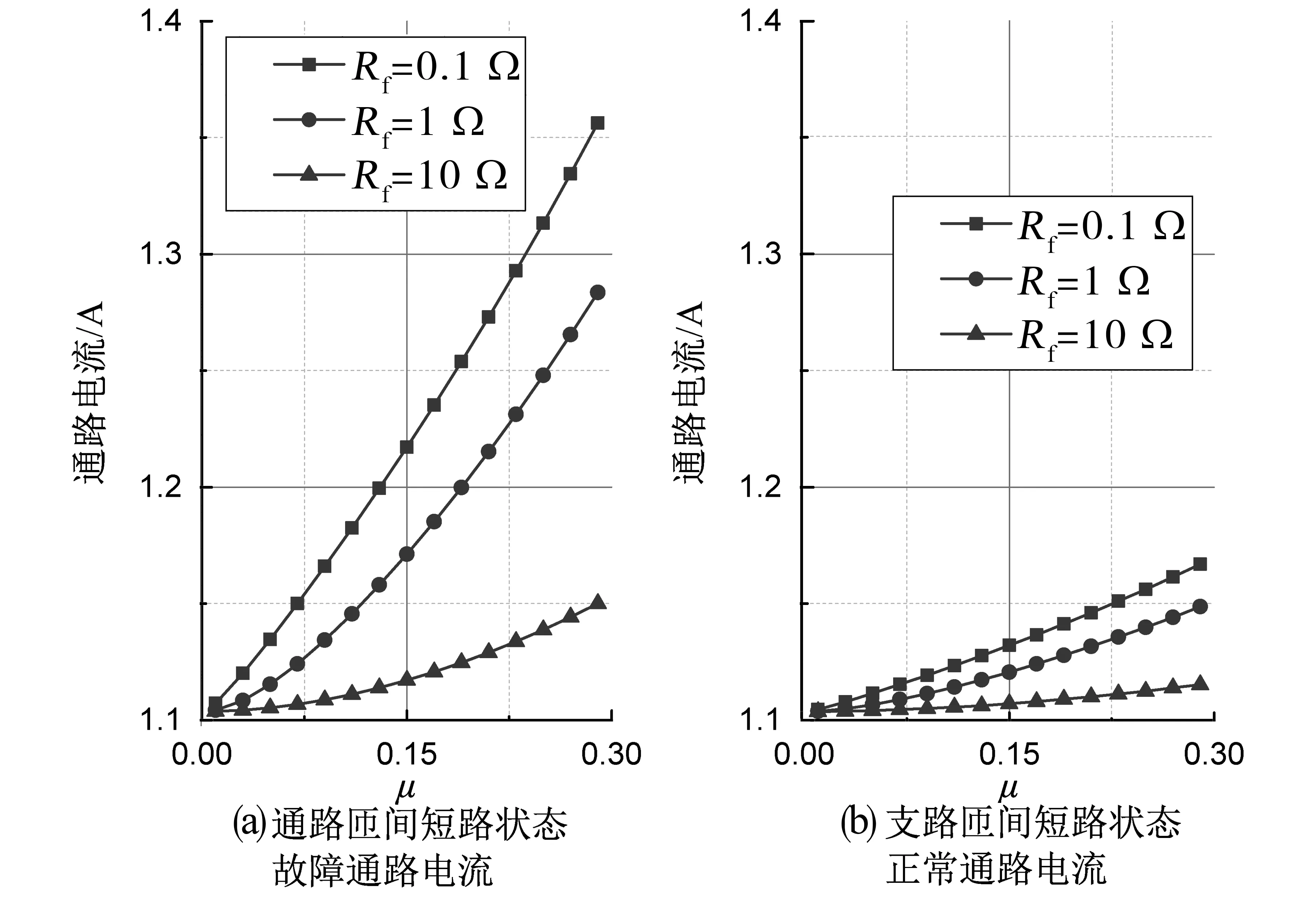
图4 不同短路电阻与短路比例,通路电流的变化曲线Fig.4 Curves of the main-path current with various valuesof the fault-resistance and the fault-ratio
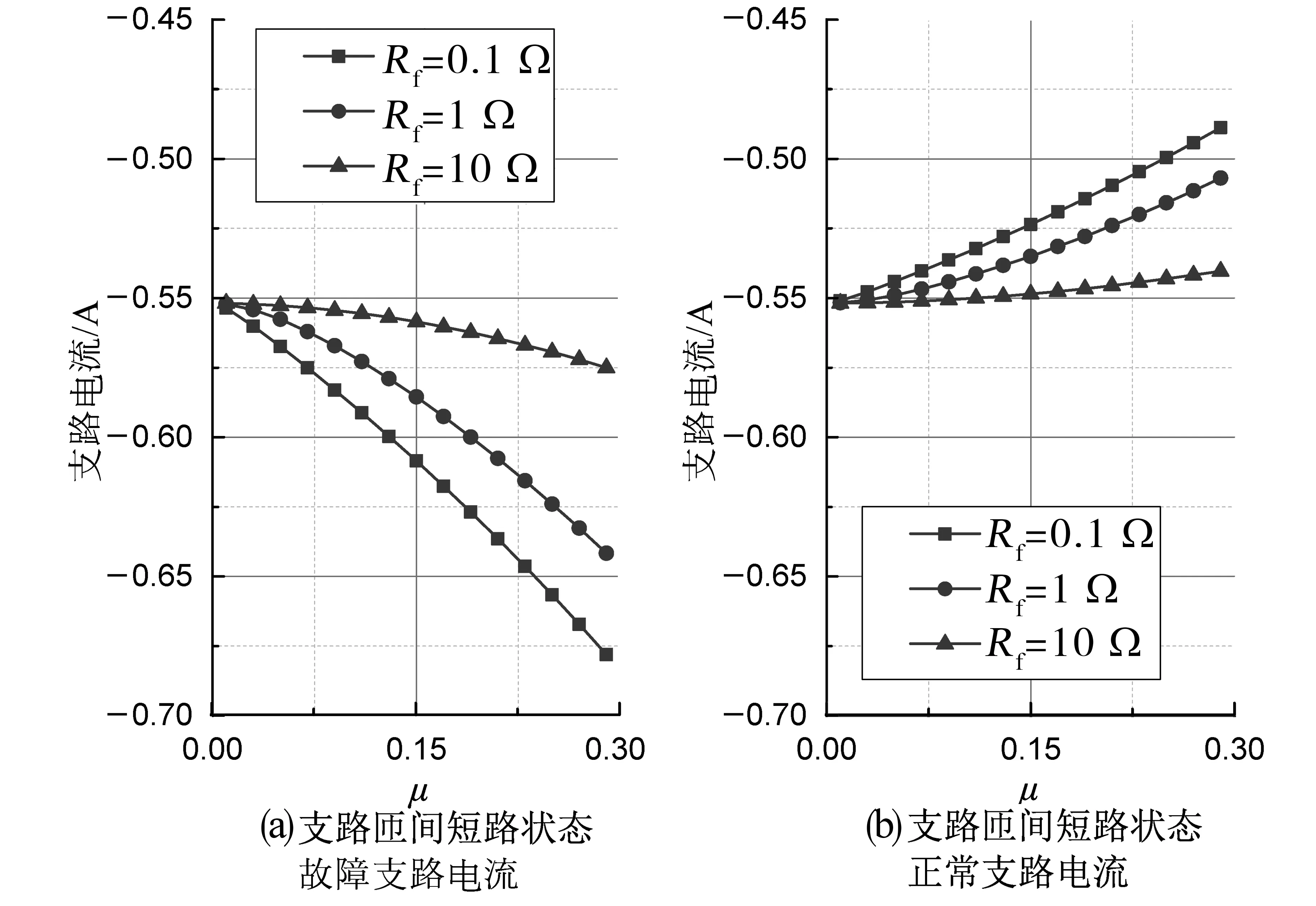
图5 不同短路电阻与短路比例,支路电流的变化曲线Fig.5 Curves of the branch-path current with various values of the fault-resistance and the fault-ratio
研究表明,不同连接方式下,通路、支路电流随故障变化而呈现不同特征。如图4 所示,两种短路状态下,通路电流均随故障程度的增加而增加,但是通路包含短路故障的情况下电流上升更为明显。如图5 所示,某一支路中发生匝间短路时,故障所在支路的电流反向降低,而另一支路电流正向增加,此时两支路间出现等效环流。
2.2 特征矢量与故障指标
为综合利用上述通路、支路电流特征,分别以电机不同相绕组作为通路,进行单相激励测试,基于电流测试结果可以定义如下特征矢量:

式中:vx(x=1,2,3)为以电机侧A,B及C相作为通路时的特征矢量;ixy(y=A,B,C)为对应连接下的激励侧A,B及C相电流;j为虚部单位。
仍然考虑故障发生于电机A相的情况,依据式(9)、式(12)的电流定义,可以得到足够长时间后特征矢量的解析表达式:

利用式(14)可以计算得到不同短路电阻与短路比例情况下特征矢量的空间位置变化,结果如图6所示,其中计算参数保持不变。可以看到:电机A相故障时,v1矢量始终保持与实轴重合,仅随故障增加而轴向移动,因而其表征了包含故障的相;v2,v3矢量关于实轴对称,且偏离距离与μ及Rf相关,因而其表征了故障的严重程度。特别地,综合式(12)可知,式(14)中v2,v3矢量的虚部实际上为此时的支路等效环流。

图6 不同短路电阻与短路比例,特征矢量的空间位置Fig.6 Space location of the feature vectors with various values of the fault-resistance and the fault-ratio
综上所述,可以给出形如下式的一般化故障指标计算式以及故障相判据。该故障指标实际上表征了支路环流的综合影响,而虚部为零的矢量增量则对应了故障的位置信息。

式中:imag[·]为取矢量虚部;Δ表示矢量相对于初始给定量的增量。
3 仿真计算
根据文献[15]中推导的感应电机故障模型,可以利用四阶龙格-库塔计算方法,开展仿真计算分析。以YE2-802-4 感应电机为建模对象,参数根据有限元计算得到:定子电阻9.06 Ω;转子电阻8.46 Ω;励磁电感379 mH;定子漏感23 mH;转子漏感28 mH;转子惯量0.002 kg·m2。A相存在28%的绕组短路,并设置短路电阻为1 Ω。驱动器分别在0 s,5 s,10 s 时刻,给定综合幅值为15 V、持续时间为1 s的等效电压阶跃激励。
图7给出了上述过程中,电机侧各相的电压、电流波形。可以看到,当故障相作为通路时,通路电流的峰值较大,而无故障相作为通路时,通路电流峰值降低。另一方面,当故障相出现在支路时,两支路构成的回路中会产生等效环流。

图7 不同通路情况下,单相激励的电机相电压、电流波形Fig.7 Voltage and current of single-phase test with different main paths
图8给出了不同短路电阻与短路比例的情况下,依据式(13)与式(15)计算得到的故障指标变化曲线。可以看到,作为影响匝间短路严重程度的主要参数,短路比例μ的增加与短路电阻Rf的降低均会使得故障指标的数值升高。

图8 不同短路电阻与短路比例,故障指标的变化曲线Fig.8 Curves of the fault indicator with various values of the fault-resistance and the fault-ratio
4 实验研究
4.1 实验平台
图9给出了实验平台连接图。

图9 实验平台连接图Fig.9 Diagram of the experimental set-up
实验感应电机型号为YE2-802-4:额定输出功率0.75 kW,额定转速1 390 r/min,额定电压380 V,额定电流2.03 A。特别地,A相中引出额外短路抽头,短路比例约为28%,通过串接20 Ω(故障程度F1)、10 Ω(故障程度F2)、5 Ω(故障程度F3)、2 Ω(故障程度F4)以及1 Ω(故障程度F5)的短路模拟电阻,可以实现故障程度的改变。实验选择2 种方案作为激励:1)逆变器激励采用Infi⁃neon公司FF150R12MS4G型IGBT,并结合2SD315A实现驱动;2)单相模拟激励采用ATTEN 公司TRP3005T 型可调直流电源实现。特别地,为了分析电机自身电阻变化对检测方法的影响,在方案2 的电机B相中额外引入了0.5 Ω 干扰电阻。信号采集与分析则基于LEM 电流传感器及HDO6054录波仪实现。
4.2 逆变器激励测试
图10 给出了逆变器驱动下正常情况与F5 故障程度下的三相电流瞬时波形,母线电压300 V,其余激励设置与仿真保持相同。从图10 中可以看到,1 s的阶跃激励持续时间已经足够使得相电流达到稳态,并且能够表现出明显的通路电流差异及支路等效环流特征。

图10 逆变器驱动,H与F5状态电机三相电流波形Fig.10 Current of three-phase test fed by inverter for H and F5
图11给出了不同故障程度下,逆变器激励实验计算结果与相同故障给定的仿真结果比较。其中,无短路引入状态为“H”,故障程度分别为“F1~F5”。可以看到,实验数据能够很好地表征故障程度的变化,并且与仿真数据的变化趋势相近。但是,两者仍存在较小的误差,分析其来源可能包含逆变器非线性、电机参数准确性、传感器对称性等因素。
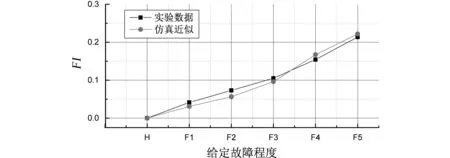
图11 逆变器驱动,实验与仿真故障指标的变化曲线Fig.11 Curves of the fault indicator of experiment and simulation fed by inverter
4.3 电阻变化影响
图12 给出了由单相模拟激励实验结果计算得到的特征矢量随故障程度增加的空间变化曲线。从图12中可以看到,在未串接额外干扰电阻时,随着故障程度的增加,特征矢量v1沿实轴方向移动,而矢量v2,v3分别近似沿虚部的正、负半轴方向移动,其变化趋势与理论分析相符。特别地,在B相引入干扰电阻后,可以看到矢量v1的移动方向不变,但整体向虚部正半轴方向偏移,而矢量v2,v3则同时向实轴的负半轴方向偏移。不难发现,虽然干扰使得3个特征矢量均出现偏移,但其中矢量v2,v3之间的相对位置变化并不明显。
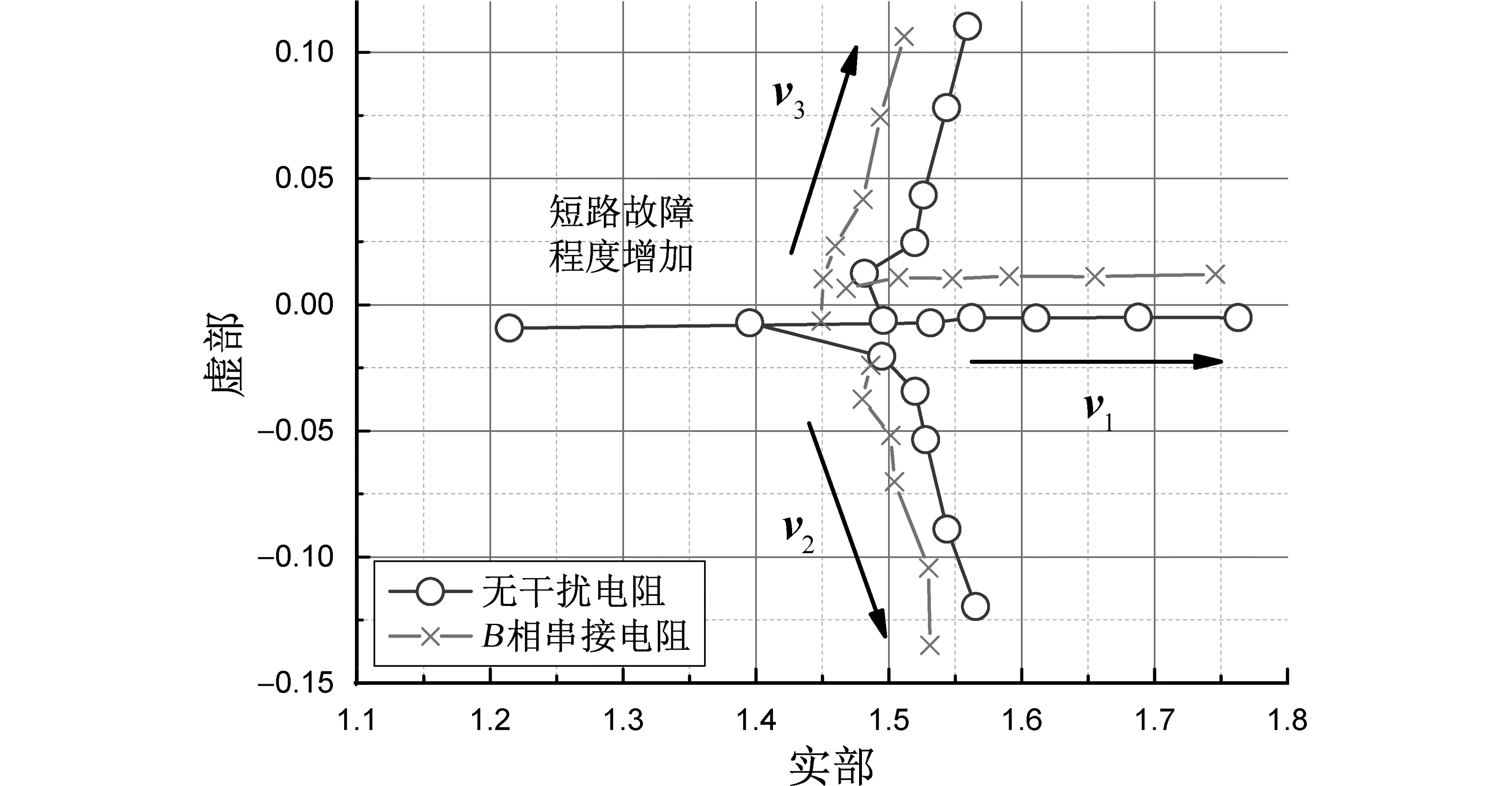
图12 单相模拟激励,特征矢量的空间位置Fig.12 Location of the feature vectors for single-phase test
图13给出了不同给定故障程度下,单相激励模拟实验结果计算得到的故障指标变化曲线。可以看到,随短路故障程度的增加,指标计算结果对应增加。同时,由于式(15)中采用的是相对于初始状态的增量计算,而且提出方法的主要故障信息来自于短路引起的支路环流,因此在串接干扰电阻前后,故障检测指标曲线基本保持相同,表现出了良好的抗干扰能力。
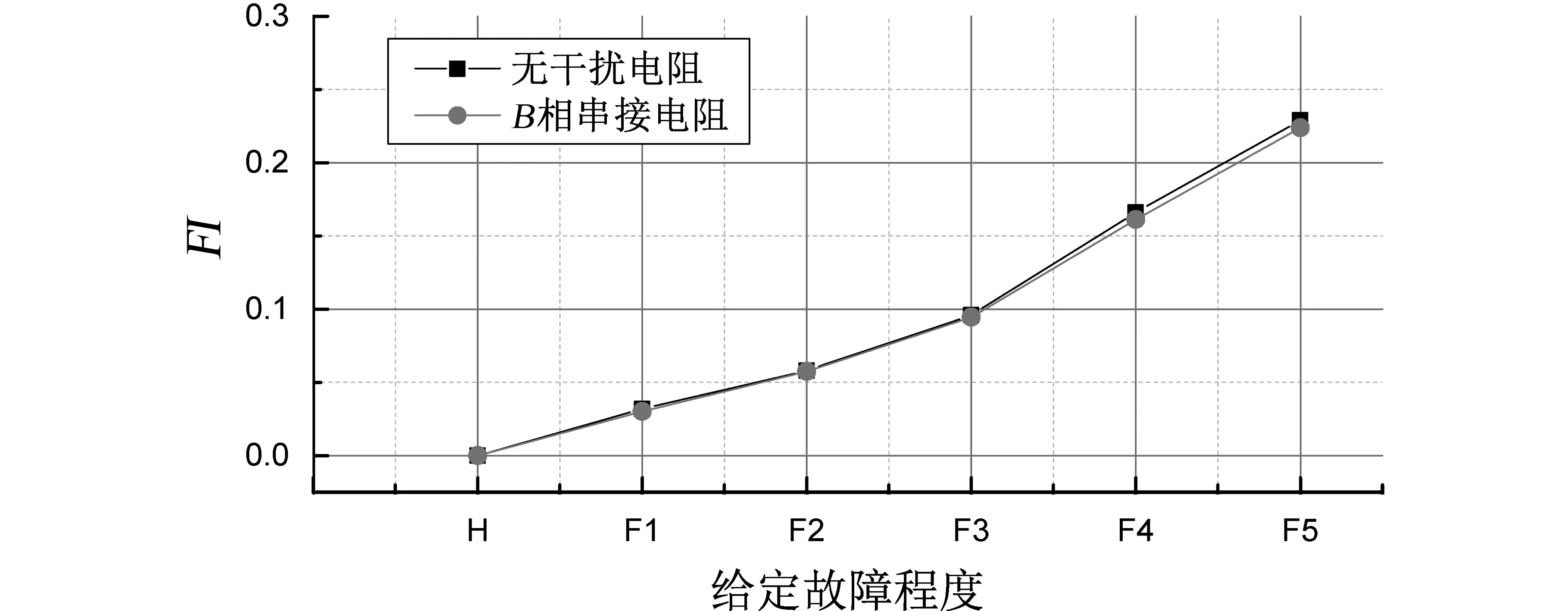
图13 单相模拟激励,故障指标的变化曲线Fig.13 Curves of the fault indicator for single-phase test
5 结论
针对感应电机相绕组发生匝间短路的情况,提出并分析了一种基于阶跃激励稳态响应的感应电机匝间短路故障诊断方法,仿真及实验结果验证了该方法的有效性,相关结论总结如下:
1)通路、支路匝间短路状态电流的解析分析显示,阶跃激励下,故障会导致通路稳态响应电流增加,并在支路短路状态下产生支路环流。
2)构建的空间特征矢量能够有效地表征电机状态的变化,并且在串接干扰电阻前后,对称矢量的相对位置变化并不明显。
3)故障指标能够在逆变器激励、单相模拟激励下,有效表征电机定子匝间短路的故障状态,操作简便,硬件需求低,具备抗干扰能力。
