一种基于调制比软启的PWM整流器启动冲击电流抑制方法

李长辉，郑丽君，吕世轩，宋建成，田慕琴

（太原理工大学煤矿电气设备与智能控制山西省重点实验室，山西太原 030024）

三相PWM 整流器因功率因数高、直流侧电压可控、网侧谐波含量低等优点[1-7]，大量应用在可再生能源电网、电力机车以及大容量变频器中，PWM 整流器在启动时会引起冲击电流，严重的时候会超过器件的承受能力，威胁系统安全。

PWM 整流器启动冲击电流的抑制措施可分为主动控制方法和被动控制方法2种。被动控制方法一般是在出现冲击电流后采取措施。文献[8]将冲击电流反馈到电流内环，达到抑制冲击电流的作用。但该方法在反馈冲击电流的同时也会反馈谐波电流，导致网侧电流总谐波畸变率增加。文献[9]检测冲击电流产生的位置，然后关断所在相的开关器件强迫电流换相。该方法由于采样延时，会使启动电流在器件关断前已经增长得较大，导致抑制效果不佳。

主动控制方法是提前做好启动冲击电流抑制措施。文献[10]在调制波中注入零序分量来抑制启动冲击电流。文献[11]提出了一种基于向主电路注入反向直流分量的变换器控制策略，以减小冲击电流。文献[12]在启动时先切除电压外环控制器，使电流参考值按照一定斜率从零上升，待直流侧电压达到参考值的90%后再接入电压外环控制器。文献[13]在启动过程中让电压参考值按照平方规律增加到给定值。文献[14]通过改进文献[13]的软启过程，在软启开始和结束阶段使电压参考值按照更平滑的抛物线规律变化，抑制冲击电流。上述几种方法都具有抑制冲击电流的能力，但是无法有效抑制启动前几个开关周期产生的冲击电流。

针对上述问题，本文从整流器开关模式角度深入分析了冲击电流产生机理，推导了开关模式持续时间与调制比的数学模型，得到了调制比与冲击电流的关系，设计了一种调制比软启方法，能从根本上抑制冲击电流。实验验证了所提方法的有效性。

1 启动冲击电流产生机理分析

1.1 网侧启动电流分析

图1所示为三相电压型PWM 整流器主电路。图1 中，ea，eb，ec为三相交流输入相电压；iga，igb，igc为三相网侧电流；ua，ub，uc为桥臂交流侧相电压；Sap，Sbp，Scp，San，Sbn，Scn为开关器件；udc为直流侧电压；idc为直流侧电流；L1为网侧滤波电感；R1为电感寄生电阻；C为直流侧母线电容；R为负载。

图1 三相PWM整流器主电路Fig.1 Main circuit diagram of three-phase PWM rectifier

如图1，假设三相电压对称，以a相为例进行分析：

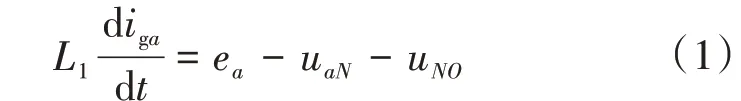
式（1）化简为

将式（2）离散化得：

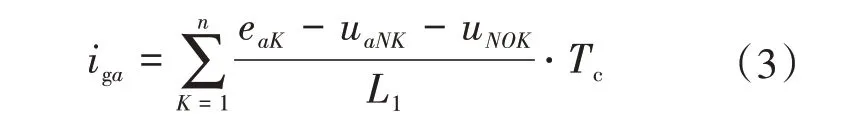
式中：K表示整流器当前工作在第K个开关周期；eaK为第K个开关周期中a相交流输入电压；uaNK为第K个开关周期中a相桥臂中点与N点的电压差；uNOK为第K个开关周期中N点与三相电源中点的电压差；Tc为开关周期时间。

由式（3）可以得出，a相电流的大小分别与ea，uaN，uNO和等效电感L1有关。其中，ea在一个开关周期内近似为常数，uaN和uNO与整流器的开关模式有关。为了精确分析启动电流，将基波周期分为6 个区间，当处于ea>eb>ec的60°区间时，根据脉冲宽度调制原理，在1 个载波周期内三相调制波电压最多可产生4种开关模式，引起电流变化。具体电路状态分析如图2所示。

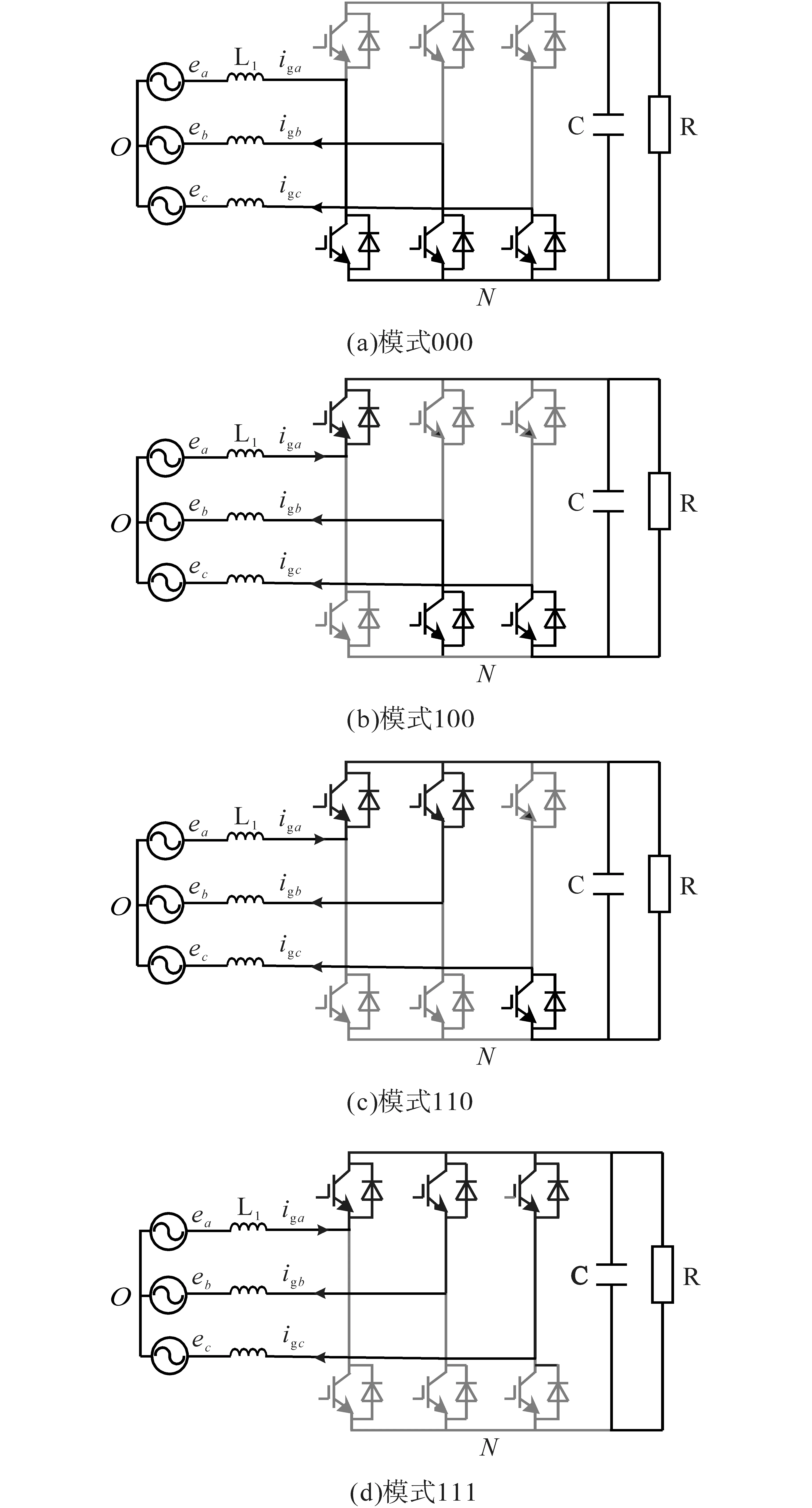
图2 区间2的开关模型电路Fig.2 Switching model circuits in interval 2

由图2 可知单一开关模式下uaN和uNO的值，式（3）表明电流增长率在电压峰值处最大，代入电压峰值Ea和uaN，uNO的值得到三相电流变化率如表1所示。

表1 不同开关模式下电流变化率Tab.1 Current rate of change under different switching modes

表1 结果显示000，111 开关模式会引起剧烈的电流增长。为了验证PWM 整流器启动冲击电流与开关模式的关系，对PWM 整流器直接启动进行仿真，各个参量变化的仿真波形如图3 所示。

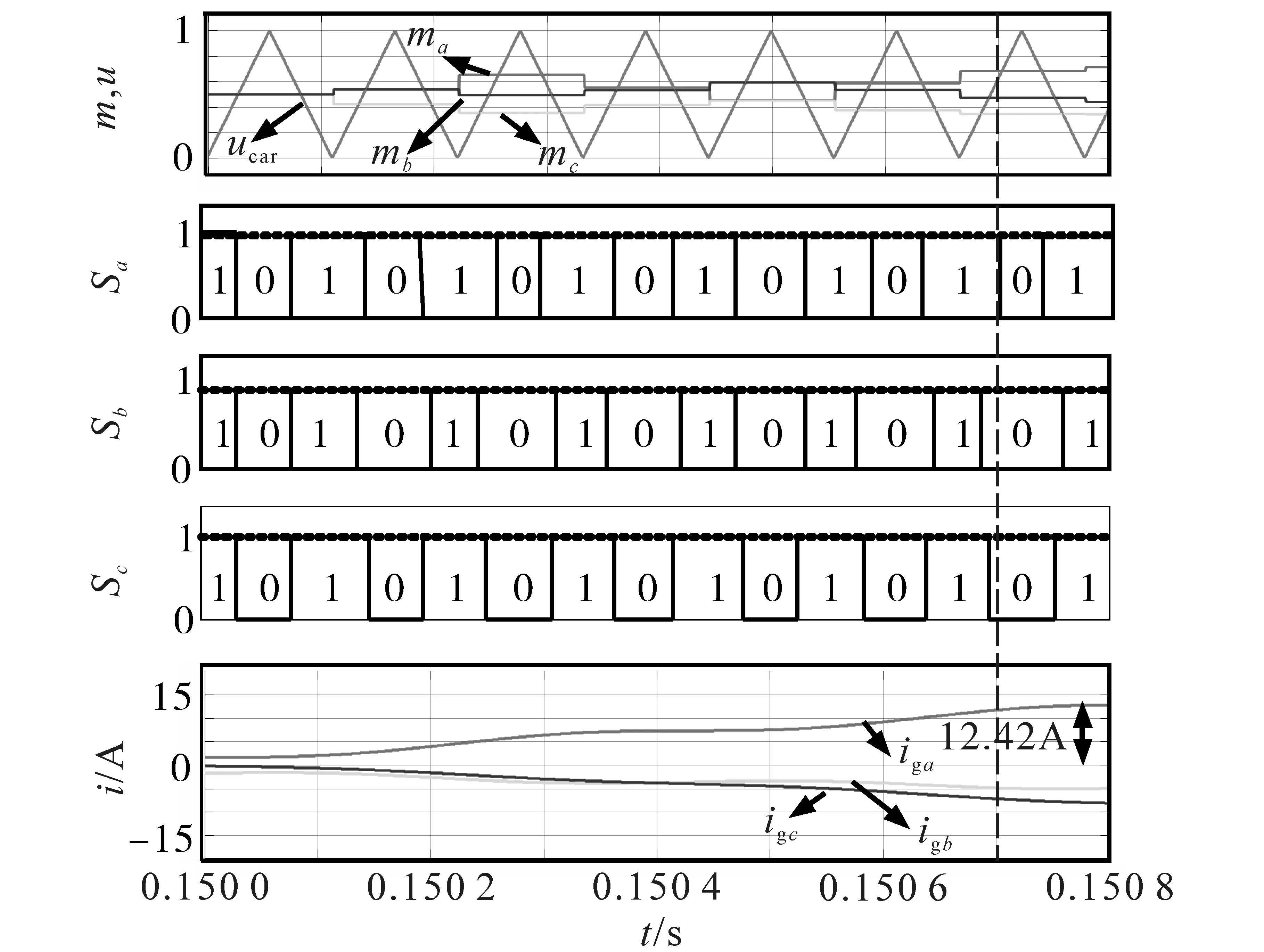
图3 PWM整流器直接启动仿真波形Fig.3 Simulated waveforms with direct start

图3中由上到下依次是网侧相电压、调制波、开关函数值、网侧电流。由于初始调制比较小，000，111 模式持续时间较长，在7 个载波周期后冲击电流为12.42 A，达到额定电流值的4 倍。综上分析，111，000 开关模式持续时间较长导致启动电流剧烈增加。

1.2 开关模式时间与调制比的关系

通过上述分析可知，冲击电流是由PWM 整流器启动时111，000开关模式持续时间较长引起的，而在一个开关周期内各个开关模式时间是由调制比决定的。因此，对调制比与111，000 开关模式间的关系进行分析，开关模式与调制比对应关系如图4所示。

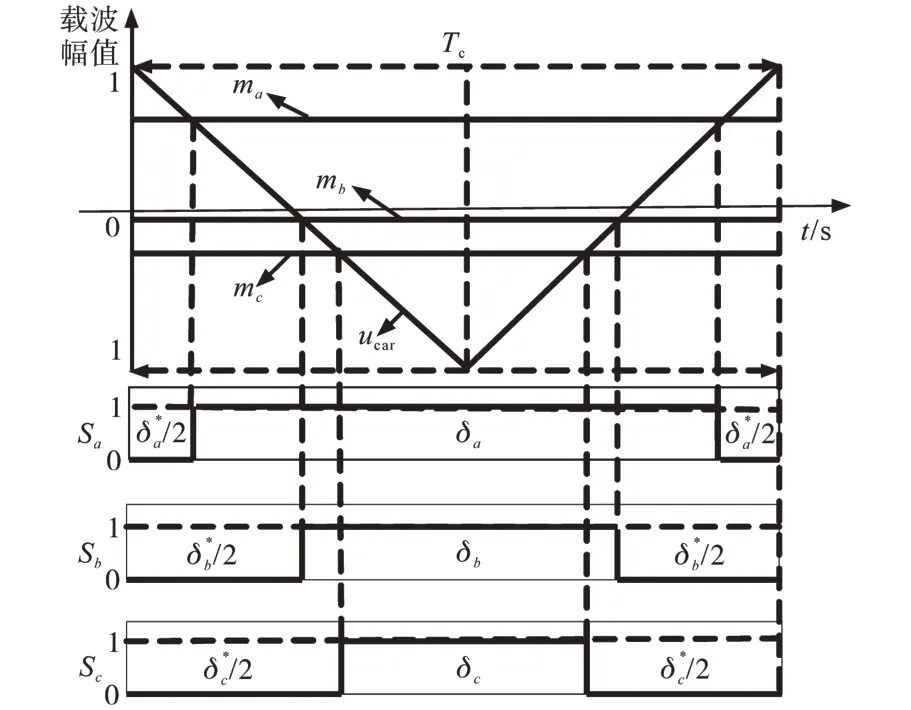
图4 规则采样法原理Fig.4 The principe of rule sampling

式中：ω为基波角频率。

根据规则采样法可得：

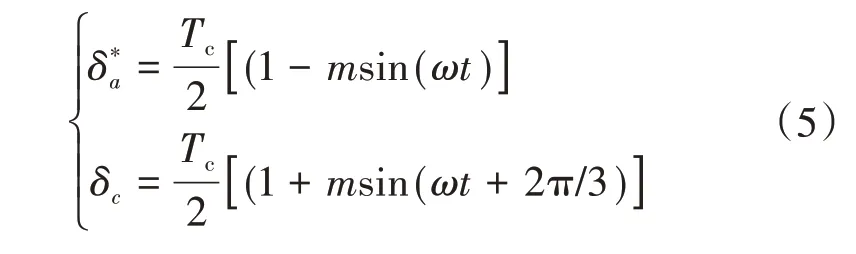
结合图4 可知，000 模式持续时间主要由δa*决定；111 模式持续时间由δc宽度决定，由于ωt+2π/3>π，所以m越小，000，111 模式持续时间越长，冲击电流也就越大。

2 启动冲击电流抑制方法

由第1 节的分析可知，PWM 整流器启动时刻调制比较小，引起较大的冲击电流。为此，提出一种调制比软启方法抑制启动冲击电流。如图5 所示，在PWM 整流器启动时设定电压参考值按照斜坡规律增加到给定值udcref，然后使生成的调制比再乘以按照倒斜坡规律函数递减到1的比例系数k，利用新得到的调制比控制PWM整流器工作。

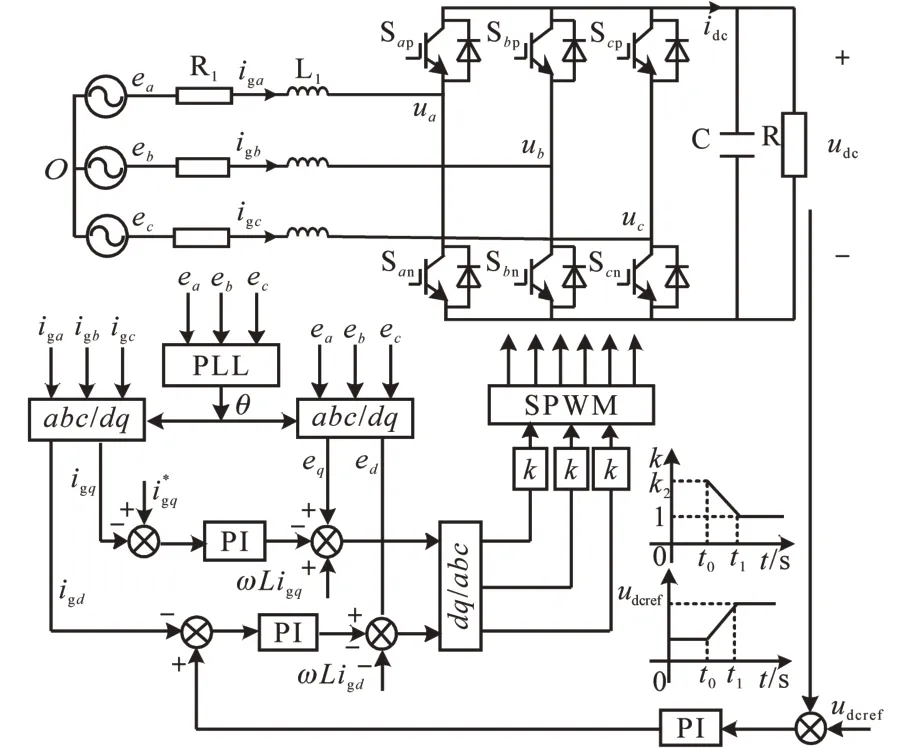
图5 PWM整流器整体控制框图Fig.5 Integral control block diagram of PWM rectifier

如图6 所示，调制比启动系数k按照倒斜坡规律变化。

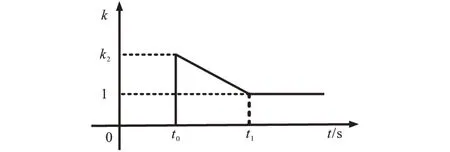
图6 调制比软启曲线Fig.6 The soft start curve of modulation ratio

由图6得调制比软启曲线函数如下：

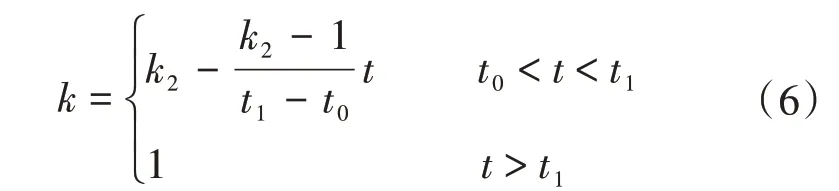
式中：t0为PWM 整流器启动时间；t1为调制比软启结束时间。

根据图5的控制器结构可得调制比计算公式：

因为本文是在开关模型电路中分析冲击电流的产生机理，而DSP 控制器是基于平均状态模型计算，所以很难精确地得到调制比与开关模式111，000 的数量关系。为了取得最佳的冲击电流抑制效果，针对曲线1 的初始值k2和调制比软启时间Δt1=t1-t0做了多组仿真分析，得到拟合关系如图7所示。

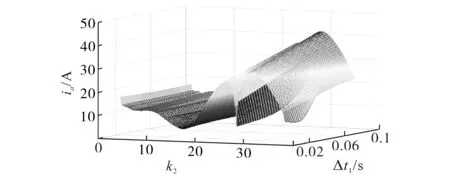
图7 冲击电流与放大系数k2和调制比软启时间∆t1的关系Fig.7 The realationship among inrush current and modulation depth and time of adaptive duty cycle

图7 表明冲击电流的大小与放大系数k2和调制比软启时间有关，当k2=15，调制比软启时间Δt1=0.06时，抑制冲击电流的效果更好。

3 实验验证

为了验证第2节提出的启动冲击电流抑制方法，搭建了整流器实验平台。分别对PWM 整流器直接启动、电压斜坡软启方法启动、双斜坡启动方法三种情况进行了实验验证。主电路参数为：网侧线电压有效值el=50 V，直流侧电压udc=100 V，网侧电感L1=2.7 mH，开关频率9 kHz，直流侧电容C=3 300 μF，直流负载R=50 Ω。

图8为PWM 整流器直接启动实验波形，启动相电流峰值达到了9.2 A。

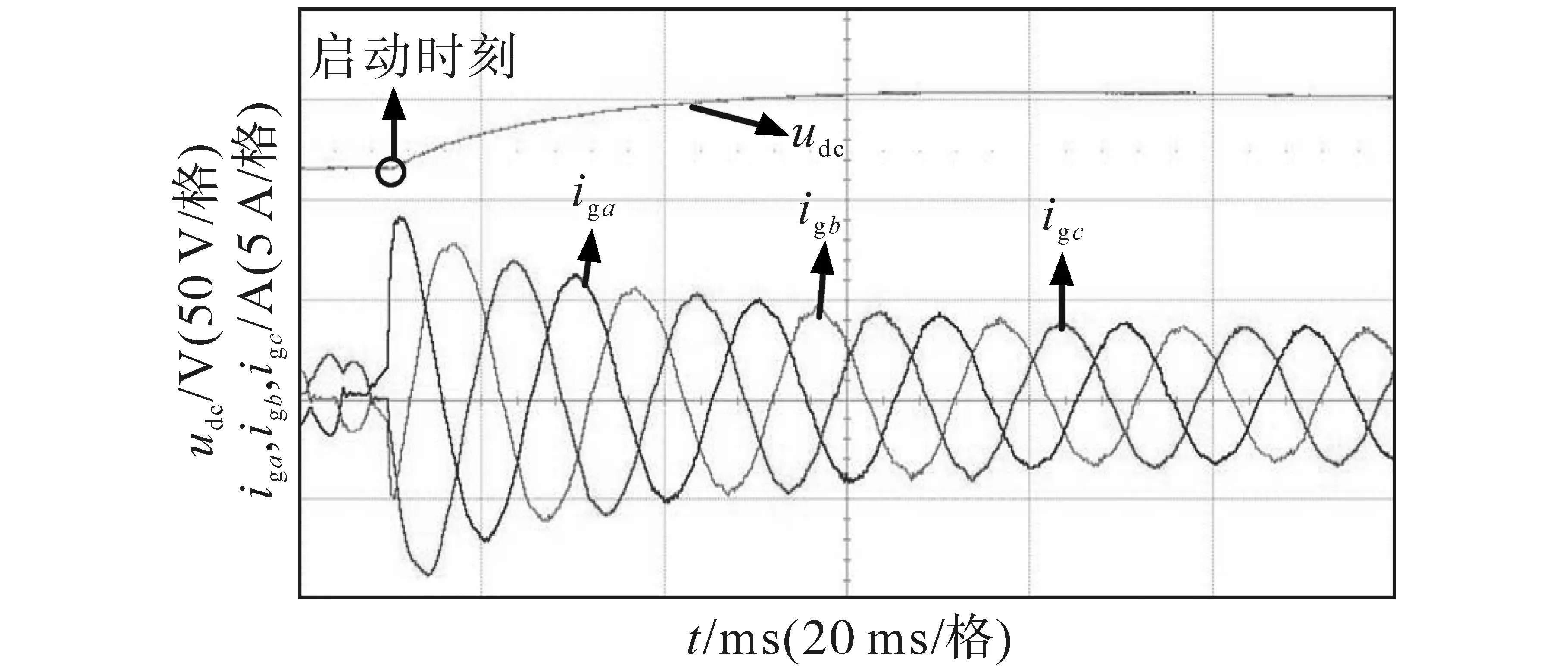
图8 直接启动的电压、电流实验波形Fig.8 Voltage and current experimental waveforms with direct start

图9为采用传统软启斜坡函数曲线作为电压的参考值得到的波形，启动冲击电流为5 A，该方法可以一定程度上抑制启动冲击电流。

图9 电压软启的电压、电流实验波形Fig.9 Voltage and current experiment waveforms with voltage soft start

图10为基于调制比软启方法得到的实验波形，启动电流为2.9 A，启动过程中电流最大值为3.5 A，稳态电流幅值为3.2 A，从根本上消除了PWM整流器启动冲击电流，实验结果与理论分析一致。

图10 调制比和电压同时软启的电压电流实验波形Fig.10 Voltage and current experimental waveforms with soft start of modulation ratio and voltage

4 结论

本文从整流器开关模式角度深入分析了PWM 整流器启动冲击电流产生机理，推导了开关模式持续时间和调制比的数学模型，得到了调制比与冲击电流的关系，从而提出一种调制比软启的启动冲击电流抑制方法。该方法在PWM 启动时设定电压参考值按照斜坡曲线缓慢增加，同时将控制器计算得到的调制波乘以线性规律递减到1 的倒斜坡函数，得到新的调制波控制三相桥臂导通关断，从根本上消除了PWM整流器启动时的冲击电流，实验验证了该方法的有效性。