基于混沌理论的汉江上游安康站1950—2014年逐月降水量特征

13

(1.北京师范大学 水科学研究院，北京 100875； 2.北京师范大学 城市水循环与海绵城市技术北京市重点实验室，北京 100875； 3.北京师范大学 地下水污染控制与修复教育部工程研究中心，北京 100875)

1 研究背景

混沌是具有确定性的动力学系统受到非线性变量的影响而产生的一种没有规则的、貌似随机的现象。混沌研究始于20世纪70年代左右，美国气象学家Lorenz[1]发表了《确定性非周期流》，发现在确定性的非线性方程中存在混沌运动，随后又在不同的动力学方程中也研究出了混沌现象。水文学领域的混沌研究起步于20世纪80年代后期，Hense[2]在研究月降雨量序列的关联维数时，同样发现了混沌现象存在于水文系统中。

30年来，许多专家学者利用混沌理论对水文学领域的各个方面进行了初步的研究，取得了丰硕的成果。迄今为止，水文学领域的混沌研究仍处于探索阶段，还有许多的问题有待于研究。Jayawardena 和Lai[3]于1994年对香港3个站点的日降雨序列和2个站点的日径流数据进行了研究分析，为香港的日降雨序列和日径流序列存在混沌性提供了比较可信的证据，虽然研究中非线性预测方法的精度不高，但对比传统的自回归移动平均法具有独特的优势。Sivakumar等[4-7]研究了新加坡6个观测站点不同序列长度的日降雨数据,证明了降水过程混沌性的存在，并使用代理数据法判定了日降雨时间序列是非线性的，还对以往研究中预测精度较低的原因进行了分析。Waelbroeck等[8]研究了墨西哥特拉克斯卡拉地区的降雨资料，发现利用累计10 d的降雨资料进行暴雨预测更有效。

对于降雨过程，特别是暴雨过程，学者普遍认为存在混沌性。王红瑞等[9]认为水文系统中混沌的提出是正确的，但对于受噪声干扰的时间序列而言，现有方法所得到的结论仅可表明其可能存在混沌特征。王文等[10]通过对水文时间序列的最大可预报时间长度、混沌特征参数估计和数据量大小等问题的讨论，指出目前水文系统中混沌的研究尚缺少谨慎合理的结论和解释。一系列基于混沌特性识别基础的预测方法的出现表明，混沌理论的应用十分有必要。Domenico等[11]以及Wang等[12]认为径流序列中存在随机成分的构成以及对初始条件的敏感，即混沌特性对径流的动态变化起决定作用，在这种情况下径流预测应该更侧重简化模型并考虑混沌理论的应用。Zounemat-Kermani[13]对日径流序列和月径流序列的研究表明其都有混沌性存在的可能，在中期径流预报中非线性局部逼近法要优于ARIMA法，在短期预报中2种方法都是可以接受的。

安康地处汉江上游，是南水北调中线工程水源地重要的水量来源，其降水量的变化在一定程度上影响着汉江径流量的变化。相关研究表明，汉江上游年降水量呈不显著减少[14]。尤其是进入21世纪以来，随着气候变化和人类活动的双重影响，汉江上游典型地区安康极端降水等问题日益突出[15]。基于此，本文利用混沌理论对汉江上游安康降水量进行特征分析，研究其降水系统动态变化作用下的径流预报，研究结果可为南水北调中线工程水量变化研究提供及时的数据和理论支撑。

2 研究区概况

安康市地处陕西省东南部，境内河流属长江流域汉江水系，处在汉江上游。河网密度为1.43 km/km2，年平均径流量为10.65亿m3。过境客水145.72亿m3，水资源总量共计252.29亿m3。汉江因其水量大、水质好而成为国家南水北调中线工程水源涵养地[16]。其中安康水文站是汉江上游控制站，位于陕西省安康市汉滨区西南城郊(109°12′E，32°25′48″N)，观测场海拔290.8 m。

3 降水特征分析

根据1929—2014年安康站的降水数据可知，其平均年降水量为788.76 mm，1938年降水量最高，达到1 392 mm。1929—2014年中年降水量<500 mm的有5 a，均出现在1950年以前。经过分析相关数据可知，1950年以前数据缺失较多，准确性较差，不能较好地表现安康站降水特征的变化，故单独统计分析1950—2014年安康站的降水数据，见图1，其平均年降水量为838.27 mm。其中，2010年降水量最高，为1 232 mm，1999年降水量最低，为526 mm。1950—2014年中共计13 a全年降水量>1 000 mm，共计3 a全年降水量<600 mm，分别是1957年、1959年、1999年。

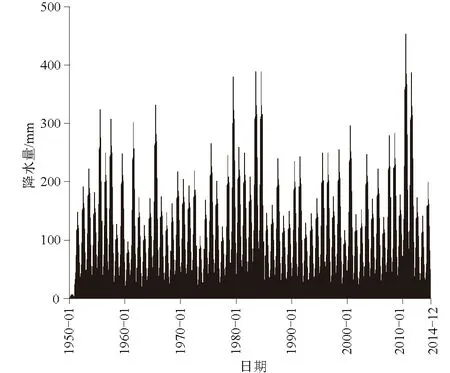
图1 1950—2014年安康站历年逐月降水量

通过图2可知，安康站降水主要集中在每年6—9月份，这4个月的降水总量占全年的近60%，7月份最多。其中2010年7月份单月降水量达到455 mm，平均每月146 mm，最低为1959年7月份降水，仅21 mm。

图2 1950—2014年安康站各月份平均降水量

若将降水过程考虑为随机过程，则降水时间序列{xn}可以写为

记：“四个全面“中，全面依法治国是很重要的一点；但现在，有法不依、执法不严的情况时有发生。您认为全面依法治国还存在哪些困境？该如何破局？

xn=fn+zn。

(1)

式中：噪声{zn}是一个离散的随机过程且期望E(zn)=0；fn是趋势函数f(t)在tn时刻的趋势值。假定噪声{zn}与趋势fn无关，趋势函数f(t)具有变化较慢的单调性。对于趋势函数，并非考虑时间间隔而进行提取，而是结合时间序列值域变化的空间进行分段的线性近似所得[17]。

对1950—2014年降水量数据，利用文献[17]所提供的去趋势算法，得到如图3虚线所示的趋势结果，可以看出安康站1950—2014年历年总降水量以及趋势变化情况整体上较为波动，可以分为4个大周期：1950—1955年呈现上升趋势，1955—1960年呈现下降趋势；1961—1965年呈现上升趋势，1966—1972年呈现下降趋势；1973—1984年呈现上升趋势，1985—1999年呈现下降趋势；2000—2010年呈现上升趋势，最近几年略有回落。

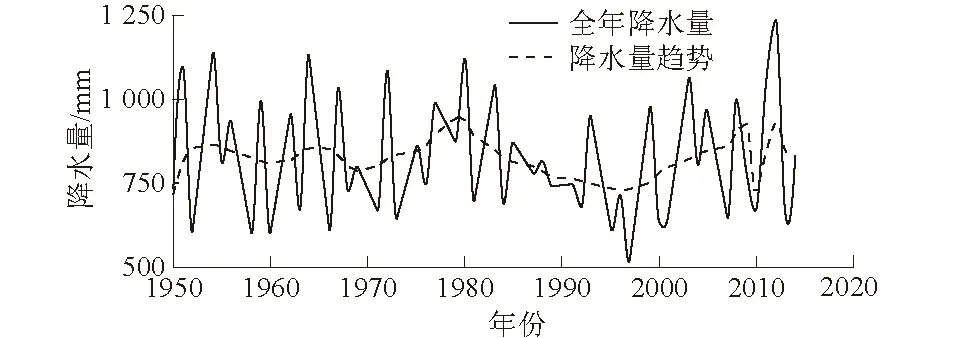
图3 安康站1950—2014年降水量以及趋势变化

4 混沌特性识别与可预测时长分析

降水过程等水文现象不能用微分方程组来描述，无法直接得到其相空间，故研究降水时间序列的混沌性首先需要重构相空间。混沌特性分析是在确定非线性系统{x(t)}的延迟时间τ、嵌入维度m后重构相空间X(t)，对X(t)进行混沌特征识别，并判断系统是否具有混沌特征，进而对其可预报性和可预报时间尺度进行分析。

4.1 相空间重构

相空间重构是水文线性混沌性识别和非线性预测的基础，Grassberger和Procaccia[18]提出了用延迟坐标法对混沌时间序列{x(t)}(t=1,2,…，N)(N指时间序列的长度)进行相空间重构，相空间中的点可以表示为

X(t)=[x(t),x(t-τ),…,x(t-(m-1)τ)]T。

(2)

式中：m为嵌入维数；τ为延迟时间，本研究中单位为月。

在重构相空间时，参数嵌入维数m和延迟时间τ的选取很关键。目前选取τ的方法有多种，包括自相关函数法、广义相关函数法等。嵌入维数m的选择方法也有多种，常用的有饱和关联维数法、伪最近邻点法等。

有些研究人员认为m和τ是有关联的[19]，对于某个实际的时间序列，其嵌入窗宽τw=(m-1)τ相对固定，近似于相轨线的平均周期。由此人们提出了一些计算m和τ的联合算法，如时间窗口法、C-C(Corelation integral)法等。

4.1.1 通过自相关函数法确定延迟时间τ

时间序列{x(t)}(t=1,2,…，N)的自相关系数rτ为

(3)

式中μ为时间序列的均值。以自相关函数首次通过0点时对应的τ值作为延迟时间τ。

4.1.2 通过G-P算法求得关联维数确定最佳嵌入维数

基于已经完成的重构相空间X(t)(t=1,2,…,T)，若给定一个邻域半径r，则可以定义关联积分Cm(r)为

(4)

式中：i、j是不同的t值；T是重构相空间序列的长度；总的相点数M=t-(m-1)τ；H为阶跃函数，当x>0时，H(x) = 1，当x≤0时，H(x) = 0；‖·‖为范数。

通常选取嵌入维数m≥2Dm+1，其中Dm是动力系统的关联维数[20]。饱和关联维数法，即G-P算法基于已经完成的重构相空间X(t)，通过求得关联积分来确定饱和关联维数。

4.1.3 利用C-C法联合求延迟时间τ和嵌入维数m

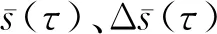
4.2 混沌特性识别

Wolf法是基于相轨迹、相平面、相体积等演化来估计Lyapunov指数的，对于重构相空间X(t)，取初始点X(t0)，并设其与最邻近点X0(t0)的距离为L0。直到t1时刻，两点间距离超过某一规定值ε>0，即L0=|X(t1)-X0(t1)|>ε，则保留X(t1)，并在X(t1)邻近另外找一点X1(t1)，使L1=|X(t1)-X1(t1)|<ε，并且与X1(t1)的夹角要尽可能小。重复上述过程，直至X(t)到达时间序列的终点N，这时追踪演化过程总的迭代次数为M，则最大Lyapunov指数λi为

(5)

4.3 可预测时间尺度

目前较常使用最大Lyapunov 指数λi的倒数来定义系统的最大可能预报时间尺度Tf，即

(6)

图4 rτ-τ关系

5 运算结果及讨论

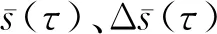
图5 C-C方法计算的延迟时间和时间窗

设定一系列m，取值从1～21变化，计算所对应的Dm。对于不同的嵌入维数m取值，作一簇lnCm(r)-lnr曲线。根据G-P关联积分法，除去斜率为0和∞的直线区段，确定其无标度区的最佳拟合直线的斜率为关联维数Dm。假若随着嵌入维数m的增加，关联维数Dm趋于饱和，此刻的Dm称为饱和关联维数，作为奇怪吸引子维数的一种估计。对安康站1950—2014年的降水时间序列数据进行处理后所得到的关联维数Dm-嵌入维数m的曲线如图6，发现关联维数Dm并非趋于饱和，而是一直在增加。所以G-P法并不能得到安康站降水时间序列数据存在混沌特性的结果，但也并非说明其不存在随机时间序列的可能。

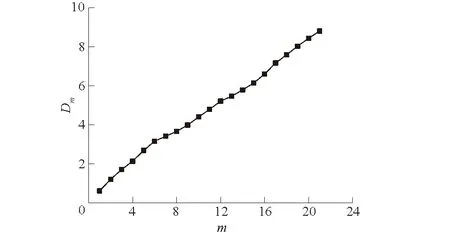
图6 关联维数Dm随嵌入维数m的变化情况

通过C-C关联积分法求得延迟时间τ和嵌入维数m，对降水时间序列重构空间，得到最大Lyapunov指数λi=0.14，说明安康站降水是存在混沌特性的，则对于1950—2014年安康站降水系统的最大可能预报时间尺度Tf≈7，说明基于现有65 a 780个月的降水数据，最大可能预报的时间长度是7个月。由于降雨与径流之间具有直接的因果关系，则基于一定序列长度的安康站汉江降雨数据，可以估计安康站汉江中期径流预报的最大可能时间尺度也应为7个月，中长期径流预报的数据时间尺度的选择更应以月为单位[22]。但基于怎样尺度的降水-径流数据以及混沌导致的降水与径流的延迟效应值得进一步探讨。

6 结 论

(1)基于安康站1950—2014年65 a来降水量趋势变化考察其降水特征，可以大致分为4个上升下降的大周期，分别为1950—1960年、1961—1972年、1973—1999年、2000—2014年。

(2)利用C-C法来确定对780个月的降水时间序列相空间重构所需的延迟时间以及嵌入维数，并同时对比自相关函数所求的延迟时间，2种方法的结果略有差异。G-P关联维法所得到的结果表明，关联维数Dm并没有随着嵌入维数的增加趋于饱和，但也并非否决了降水时间序列存在混沌的可能性。最大Lyapunov 指数λi=0.14，说明安康站降水是存在混沌特性的，对于1950—2014年安康站降水系统的最大可能预报时间尺度Tf≈7，即根据65 a共780个月的降水数据最大可能预测到接下来7个月的降水量。

(3)多个方法所求的结果不一致，表明了混沌特性存在的可能性需要进一步分析。在此基础上将多种方法的预测值进行相互比较，不同方法使用时所考虑的噪声对混沌特性识别的影响可能导致了所求得结果的差异性。