考虑渗流影响的幂强化-理想塑性模型圆形隧洞围岩弹塑性新解
2021-07-12
(1.唐山工业职业技术学院, 河北 唐山 063299;2.长安大学 建筑工程学院, 西安 710061)
1 研究背景
山岭深埋隧洞岩体经常存在于丰富的地下水中,这些深埋隧洞在开挖过程中不仅受到开挖扰动影响,还会受到地下水的影响,主要表现为渗流中的外水压力与作用于隧洞围岩上的渗流体积力[1],因此,对考虑渗流影响的隧洞围岩进行弹塑性分析具有重要的理论意义。李宗利等[2]基于Mohr-Coulomb准则得出了理想弹塑性模型下考虑渗流影响的深埋圆形隧洞围岩弹塑性解;王睢等[3]基于Drucker-Prager(DP)准则得出了理想弹塑性模型下有压圆形隧洞围岩弹塑性解;黄阜等[4]基于Hoek-Brown准则得出了理想弹塑性模型下圆形洞室围岩弹塑性解;潘继良等[5]基于广义空间滑动面(SMP)准则得出了理想弹塑性模型下考虑渗流和剪胀的圆形巷道围岩弹塑性解;张常光等[6-7]基于统一强度理论得出了弹脆塑性模型下圆形隧洞围岩弹塑性解;张黎明等[8]基于应变非线性软化模型得出考虑渗流影响的圆形隧洞围岩弹塑性解。
从上述文献可以看出,对于圆形隧洞围岩的研究虽然均考虑了渗流影响,但是采用的本构模型多是基于理想弹塑性模型、弹脆塑性模型或应变非线性软化模型,文献[9]指出对于一些应变强化效应较强的石灰岩、泥岩等岩石材料采用理想弹塑性模型是不合适的,采用幂强化-理想塑性模型较为合理,并给出了基于DP准则下不考虑渗流影响的圆巷弹塑性解。同时上述文献采用的强度准则多是未考虑中间主应力效应的Mohr-Coulomb准则、Hoek-Brown准则,以及考虑中间主应力效应的DP准则、广义SMP准则和统一强度理论,并未在理论上给出采用哪种强度准则对隧洞围岩进行弹塑性分析比较合理,文献[10]指出采用不同的强度准则对结构的强度分析影响很大,即强度理论效应,采用不同的强度准则得出的结果可能比计算方法影响大得多。而目前对考虑渗流影响的幂强化-理想塑性模型圆形隧洞围岩采用哪种强度准则进行弹塑性分析才比较合理,相关文献研究甚少。
本文首先对4种常用的岩土材料强度准则进行归纳总结,进而得出平面应变统一线性方程;然后考虑渗流影响,推导了幂强化-理想塑性模型圆形隧洞围岩的弹塑性解,最后探讨了强度理论效应、幂强化参数和孔隙水压力对圆形隧洞围岩弹塑性分析的影响。
2 幂强化-理想塑性模型
幂强化-理想塑性材料的三轴压缩本构关系[9]见图1,图1中σs为岩石的屈服极限。

图1 幂强化-理想塑性模型本构关系
在幂强化阶段:
(1)
在理想塑性阶段:
σi=σs。
(2)
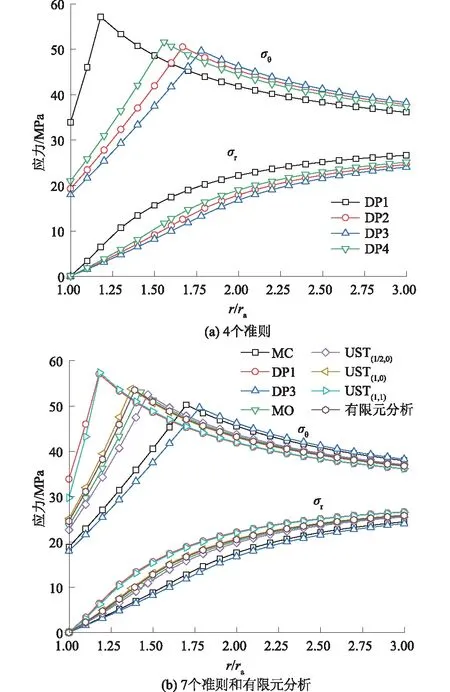
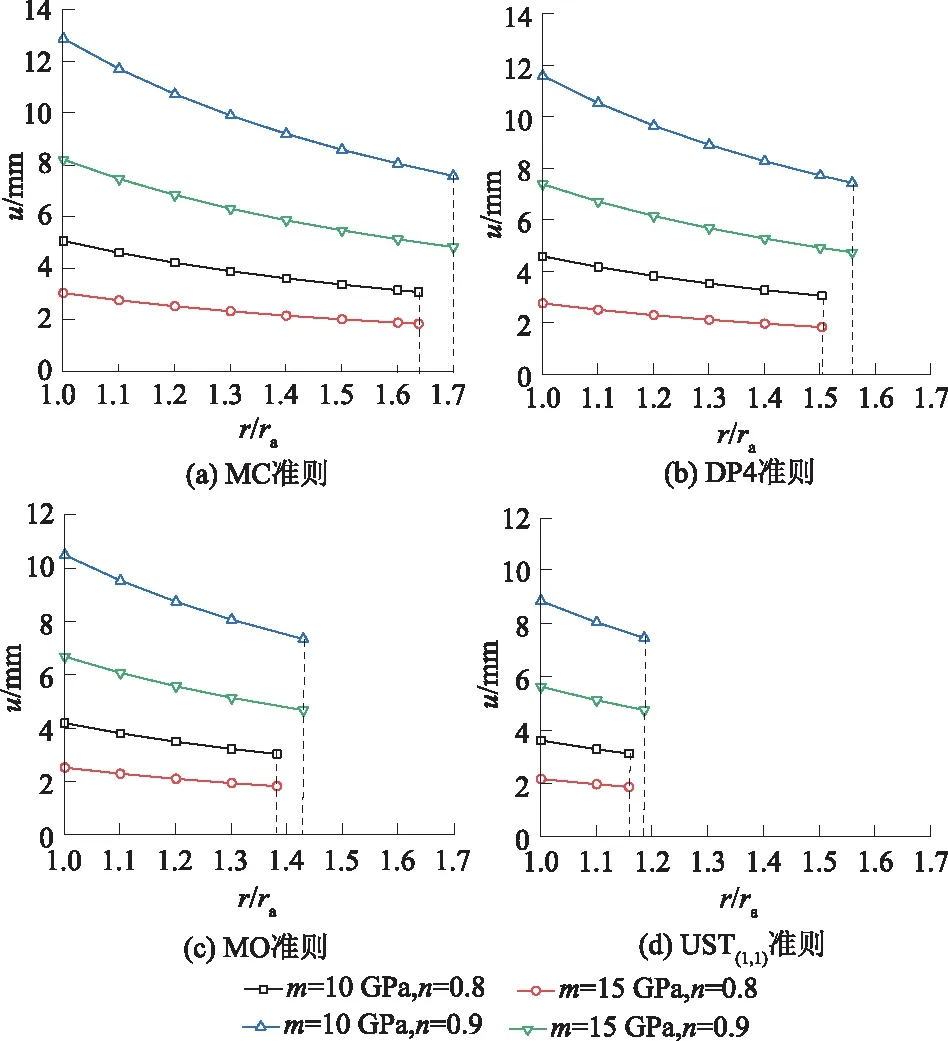
式中:m为幂强化系数(GPa);n为幂强化指数,且0 (4) 式中:σθ、σr和σz分别为隧洞围岩切向应力、径向应力和轴向应力;εθ、εr和εz分别为隧洞围岩切向应变、径向应变和轴向应变;ν为泊松比。 假定该材料的体积是不可压缩的[11],计算中取泊松比ν=0.5,因此对于轴向无限长(εz=0)的圆形隧洞,根据广义Hooke定律求解可得:σz=(σr+σθ)/2。同时由于隧洞围岩切向应力σθ、径向应力σr和轴向应力σz相互正交,当隧洞围岩压力系数为1时,切向应力σθ、径向应力σr和轴向应力σz可看作3个主应力,即σ1=σθ、σ3=σr、σ2=σz,于是3个主应力关系可以用式(5)表示。 σ2=(σ1+σ3)/2 。 (5) 而且对于该模型来说,在幂强化阶段中材料的弹性变形与塑性变形同时产生,其变形一直处于弹塑性状态,即不出现弹性区和塑性区[11]。 采用岩石力学的符号记法:压应力为正,拉应力为负,主应力大小σ1≥σ2≥σ3,按照应力代数值大小进行排序。反映3个主应力关系的4种常用岩土材料强度准则如下所述。 Mohr-Coulomb准则是岩土工程中最常用的强度准则,其不足之处在于该准则未包含中间主应力,其表达式为[12] σ1=AMCσ3+BMC。 (6) 其中: 式中:c0为黏聚力;φ0为内摩擦角。 Drucker-Prager准则考虑了中间主应力和静水压力对屈服和破坏的影响,根据π平面上DP准则与Mohr-Coulomb准则的相对关系得出了平面应变状态下的DP系列准则,其表达式为 (7) 其中: 式中:I1为第一应力不变量;J2为第二应力偏量不变量;α和k为材料强度参数,式(7)中参数k=3αc0cotφ0。 将式(5)结合式(8),然后代入式(7),得到 σ1=ADPσ3+BDP。 (9) 其中: 文献[13]给出了参数α的4种表达公式:分别称作DP1(MC准则外角点外接圆)、DP2(MC准则内角点内接圆)、DP3(MC准则内切圆)和DP4(MC准则等面积圆)。 通过对多种岩石真三轴试验,Mogi提出的强度准则表达式为[14-15] τoct=f(σ13) 。 (10) 其中: (11) 式中:τoct为八面体剪应力;σ13为与中间主应力平行破裂面上平均主应力;f为单调递增函数。 Al-Ajmi等[16]将线性Mogi经验强度准则与Coulomb准则结合,建立了Mogi-Coulomb准则,其表达式为 (12) 将式(5)、式(11)、式(12)相结合得到平面应变状态下的Mogi-Coulomb准则表达式为 σ1=AMOσ3+BMO。 (13) 其中: 高江平等[17-18]考虑菱形十二面单元体所有应力分量建立了三剪应力统一强度理论,其表达式为: (14) sinφs={(1+b)(1+sinφ0)+[c(1+sinφ0)- (1-sinφ0)b]μ-(1+c)(1-sinφ0)}/ [(1+b)(1+sinφ0)+(1+c)(1-sinφ0)], 此时μ≠1; (15) sinφs={(1+b)(1+sinφ0)+[c(1+sinφ0)- (1-sinφ0)b]-(1+c)(1-sinφ0)}/ [(1+b)(1+sinφ0)+(1+c)(1-sinφ0)], 此时μ=1 ; (16) (17) 式中:φs和cs为材料的统一内摩擦角和统一黏聚力;μ为中间主应力系数(0<μ≤1),σ2=μ(σ1+σ3)/2,μ可由理论和实验来确定,在弹性区,μ=2ν(ν为泊松比),在塑性区,μ→1;b为中间主剪应力τ12及作用面上正应力σ12综合影响的作用系数(0≤b≤1);c为最小主剪应力τ23及作用面上正应力σ23综合影响的作用系数(0≤c≤1)。当b=0,c=0时退化为Mohr-Coulomb准则;当b=1,c=0时为双剪应力准则;当b=1,c=1时为三剪应力准则;当b、c分别取0~1之间其他值时得到一系列新的强度准则。 本文取μ=1,则σ2=(σ1+σ3)/2。将式(16)和式(17)代入式(14),得到平面应变状态下表达式为 σ1=AUSTσ3+BUST。 (18) 其中: 为了表达方便,本文将b=0.5,c=0时记为UST(1/2,0);b=1,c=0时记为UST(1,0);b=1,c=1时记为UST(1,1)。 综合以上4种常用的强度准则,可以得到平面应变统一线性方程为 σ1=Aσ3+B。 (19) 通过改变参数A和B来得到不同的强度准则,进而采用式(19)对圆形隧洞围岩进行弹塑性分析。 设圆形深埋隧洞围岩连续、均匀及各向同性,轴向无限长且水平延伸,其断面图见图2。 图2 圆形隧洞力学模型 隧洞开挖半径为ra,塑性区半径为rp,计算区域内半径为βra,原岩应力为p0,隧洞支护力为pa。假定岩体的渗流属于层流,渗流过程符合达西定律,在隧洞洞壁处的孔隙水压力为0,距离隧洞无穷远处的孔隙水压力为pb,不考虑计算区域水和岩土体自重,将渗流问题简化为轴对称恒定渗流平面应变问题,于是渗流连续微分方程为 (20) 式中pw(r)为半径r处的孔隙水压力。 选取渗流场的计算区域和圆形隧洞的计算区域均为βra,其中β=30。文献[2]指出β=30即可满足工程需要的精度要求。 将边界条件pw(r)|r=ra=0,pw(r)|r=βra=pb代入式(20)可得渗流连续微分方程的解为 (21) 轴对称平面应变问题的渗透水压力为体积力,忽略渗透体积力中的浮力部分,则考虑渗透体积力的平衡微分方程为[5] (22) 式中ξ为岩石等效孔隙水压力系数。 根据前面符号法则可知:在围岩塑性区内,大小主应力分别为切向应力σθ和径向应力σr,即σ1=σθ,σ3=σr,由式(19)得到 σθ=Aσr+B。 (23) 在围岩塑性区,将式(23)代入式(22),结合边界条件r=ra,σrp=pa得到围岩塑性区应力的表达式为: (24) (25) 式中上角标加“p”代表塑性区,下同。 在围岩幂强化区,将式(5)代入式(3),并根据σr<σθ,得到 (26) 将式(26)代入式(22),得到 (27) 将式(1)代入式(27),得到 (28) 将几何方程εr=du/dr,εθ=u/r及εz=0代入体积不可压缩条件εr+εθ+εz=0可得 du/dr+u/r=0 ; (29) 求解得到 u=C1/r。 (30) 式中C1为积分常数。 进一步得到 εr=-C1/r2,εθ=C1/r2。 (31) 将式(31)结合εz=0代入式(4)得到 (32) 将式(32)代入式(28)并结合边界条件r=βra,σrep=p0+ξpb可得 (33) 将式(33)代入式(26)得到 (34) 式中上角标加“ep”代表幂强化区,下同。 由接触条件:σrep|r=rp=σrp|r=rp,σθep|r=rp=σθp|r=rp可以得到: AC3+B。 (36) 其中: 由式(35)和式(36)可求得围岩塑性区半径计算公式为 2nC2+B](βra)2n。 (37) 式(37)是关于rp的超越方程,需要试算或者迭代求解。求解出rp后,根据式(35)和式(36)可得出 将式(38)代入式(33)和式(34)可得到围岩幂强化区的应力为: (39) 将式(38)代入式(30)即可得出围岩的位移为 (41) 对于具体的工程算例,将本文解与有限元软件midas GTS NX的计算结果进行了对比,并探讨了强度理论效应、幂强化参数及孔隙水压力对圆形隧洞围岩弹塑性分析的影响。选取围岩参数如下[9]:围岩的单轴抗压强度σc=20 MPa,黏聚力c0=6 MPa,内摩擦角φ0=25°,剪切弹性模量G=15 GPa, 泊松比ν=0.5,隧洞半径ra=3 m,原岩应力p0= 15 MPa,孔隙水压力pb=10 MPa,支护力pa=0 MPa,岩石等效孔隙水压力系数ξ=1。幂强化阶段中m=G=15 GPa,n=0.9。 不同强度准则和采用有限元计算的塑性区、幂强化区的应力分布见图3。从图3可以看出:整体来说隧洞围岩均出现了塑性区,切向应力随半径的增大先增大后减小,并且峰值出现在塑性区和幂强化区交界面处。围岩塑性区半径越大,切向应力峰值、径向应力以及洞壁处的切向应力越小。 图3 强度理论效应对应力的影响 从图3(a)可以看出:不同的DP准则得到的围岩应力分布差别较大,DP2、DP4准则求解的切向应力峰值、径向应力以及洞壁处的切向应力均处在DP1、DP3准则之间。 从图3(b)可以看出:DP1、UST(1,1)准则下的应力分布非常接近,其中径向应力几乎重合,切向应力峰值几乎相等,洞壁处切向应力DP1> UST(1,1),这两个准则高估了围岩的实际强度;DP3、MC准则下应力分布非常接近,DP3准则下的切向应力峰值和洞壁处的切向应力略小于MC准则,严重低估了围岩的实际强度; MO、UST(1/2,0)、UST(1,0)3个准则下的切向应力峰值、径向应力以及洞壁处的切向应力数值和有限元分析结果非常接近,且介于UST(1,1)准则与MC准则之间,这是由于UST(1,1)准则将中间主应力效应进行过高估计,而MC准则未考虑中间主应力效应的原因。 综上所述,DP3、MC准则得到的应力最小,采用该准则使设计偏于保守;DP1、UST(1,1)准则得到的应力最大,过高估计了中间主应力效应,采用该准则使设计偏于危险;MO、UST(1/2,0)、UST(1,0)3个准则考虑的中间主应力效应处于某个中间值且和有限元分析结果接近。因此,对于幂强化-理想塑性隧洞围岩的弹塑性分析,首先推荐使用MO、UST(1/2,0)、UST(1,0)准则,其次可使用DP2、DP4准则,不建议使用DP3、MC准则,谨慎使用DP1、UST(1,1)准则。 为了分析幂强化参数对围岩塑性区半径和位移的影响,同时考虑一般岩土材料幂强化指数n>0.5[9],本小节取幂强化系数m分别为10 GPa和15 GPa, 幂强化指数n分别为0.8和0.9,其他参数同工程算例中围岩参数。图4给出了4个具有代表性的强度准则下,塑性区位移和幂强化参数之间的关系,图中虚线表示塑性区半径。 图4 幂强化参数对塑性区位移和半径的影响 从图4可知,当n值相同时,围岩塑性区半径随着m值的改变不变化,围岩塑性区位移随m值减小而增大,且在洞壁处的位移最大。同时m值越小,围岩塑性区位移曲线斜率越大,但在围岩塑性区同一点处,位移增长的比例相同,与强度准则无关,这点可以从式(41)推导出来。比如当n=0.9时,m=10 GPa比m=15 GPa围岩塑性区同一点处的位移均增大了56.91%。当m值相同时,随n值的增大,围岩塑性区半径和位移均增大,这是由于随n值的增大,材料的应变强化效应逐渐减弱的缘故。若n=1,则本文本构模型即为理想弹塑性模型,此时求得的围岩塑性区的位移最大,可见若忽略应变强化效应,按照理想弹塑性模型进行计算则使支护设计偏于保守。 为了分析孔隙水压力对围岩塑性区半径和位移的影响,本小节取不考虑孔隙水压力(pb=0 MPa)和考虑孔隙水压力(pb=5 MPa和pb=10 MPa),其他参数同工程算例中围岩参数。MO准则下孔隙水压力对围岩应力分布的影响见图5;MO准则下孔隙水压力对塑性区位移和半径的影响见图6,其中虚线表示塑性区半径。其他3个代表性的强度准则和MO准则情况类似,限于篇幅,不再展开。 图5 MO准则下孔隙水压力对围岩应力分布的影响 图6 MO准则下孔隙水压力对塑性区位移和半径的影响 从图5可以看出, 不考虑孔隙水压力与考虑孔隙水压力的圆形隧洞周边均产生了塑性区, 且塑性区半径、 径向应力和切向应力峰值均随孔隙水压力增大而增大。 在塑性区内, 塑性应力解几乎重合, 这是由于塑性应力解仅和强度准则有关; 在强幂化区内, 径向应力和切向应力均随半径的增大而逐渐趋近于p0+ξpb(对应于本小节即15、 20、25 MPa)。 从图6可以看出,随孔隙水压力的增大,围岩塑性区半径增大,当孔隙水压力pb为0、5、10 MPa时,围岩塑性区半径分别为3.120 4、3.714 6、4.287 0 m,可见考虑孔隙水压力(pb为5、10 MPa)时围岩塑性半径比不考虑孔隙水压力(pb为0 MPa)时分别增大了19.04%和37.39%;而且随孔隙水压力的增大塑性区位移也增大,尤其是洞壁处位移,当孔隙水压力pb为0、5、10 MPa时,洞壁处位移分别为1.99、3.93、6.69 mm,可见考虑孔隙水压力(pb为5、10 MPa)时洞壁处位移比不考虑孔隙水压力(pb为0 MPa)时分别增大了97.49%和238.18%,可见不考虑孔隙水压力将使隧洞围岩支护设计偏于危险。 本文通过对4种岩土材料强度准则进行归纳总结,推导了考虑渗流影响的幂强化-理想塑性模型的圆形隧洞围岩弹塑性解,并与有限元结果进行了对比分析,主要得到了如下结论: (1)本文考虑渗流影响、幂强化-理想塑性模型,将圆形隧洞围岩由内而外划分为塑性区、幂强化区,并对塑性区、幂强化区的应力、位移以及塑性区半径进行了理论推导,得到了包含4种常用岩土强度准则的统一解,该解答形式简单且便于应用。 (2)幂强化-理想塑性模型隧洞围岩的强度理论效应显著,强度准则的选取对于计算十分重要。推荐使用MO、UST(1/2,0)、UST(1,0)准则,其次可使用DP2、DP4准则,不建议使用DP3、MC准则,谨慎使用DP1、UST(1,1)准则。 (3)对于幂强化系数m值和幂强化指数n值来说,当n值相同时,围岩塑性区半径随m值的改变不变化,围岩塑性区位移随m值减小而增大,且在洞壁处的位移最大。同时m值越小,围岩塑性区位移曲线斜率越大,但在围岩塑性区同一点处,位移增长的比例相同,与强度准则无关;当m值相同时,随n值的增大,围岩塑性区半径和位移均增大。在实际工程中,一般岩石材料受到荷载之后都会产生应变强化效应,因此分析幂强化指数n的影响具有重要实际意义。 (4)考虑孔隙水压力对隧洞围岩的塑性区半径和位移的影响很显著。以MO准则为例,考虑孔隙水压力(pb为5、10 MPa)时围岩塑性半径比不考虑孔隙水压力(pb为0 MPa)时分别增大了19.04%和37.39%,考虑孔隙水压力(pb为5、10 MPa)时洞壁处位移比不考虑孔隙水压力(pb为0 MPa)时分别增大了97.49%和238.18%。因此不能忽视孔隙水压力在隧洞围岩弹塑性分析中的影响。3 岩土强度准则的平面应变统一线性方程
3.1 Mohr-Coulomb(MC)准则
3.2 Drucker-Prager(DP)系列准则
3.3 Mogi-Coulomb(MO)准则
3.4 统一强度理论(UST)
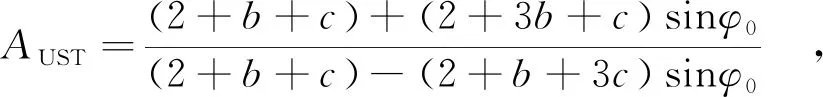
3.5 强度准则平面应变统一线性方程
4 圆形隧洞围岩弹塑性新解
4.1 渗流场计算

4.2 渗流作用下隧洞围岩应力、位移和塑性区半径
5 工程算例及参数分析
5.1 强度理论效应的影响
5.2 幂强化参数的影响
5.3 孔隙水压力的影响


6 结 论
