反倾岩质边坡弯曲倾倒-剪切滑移破坏分析方法研究
2021-07-12
(贵州省交通规划勘察设计研究院股份有限公司,贵阳 550001)
1 研究背景
倾倒破坏是岩质边坡的一种主要破坏模式,常见于具有反倾结构的自然或人工边坡中,如许多水利水电[1-2]、高速公路[3]、矿山[4]等工程都出现了大量的反倾边坡倾倒破坏问题。自20世纪60年代,反倾边坡倾倒破坏的工程地质问题才开始引起学者们的注意,Ashby[5]提出了评价该类破坏的简单准则,并首先将该类破坏命名为“倾倒”,Goodman[6]将倾倒破坏归纳分类分为块状倾倒、弯曲倾倒和块状-弯曲倾倒3种主要模式。
国内外学者针对岩质边坡倾倒破坏的分析方法展开了研究,并取得了较丰富的成果。Goodman[6]首次基于极限平衡原理提出了针对块状倾倒变形的分析方法(简称G-B法);高连通等[7]考虑地下水作用,对G-B方法进行了改进;Aydan等[8]建立悬臂梁弯曲模型,提出了针对弯曲倾倒破坏的稳定性分析方法,并通过底摩擦试验验证了该方法的适用性及有效性;Adhikary等[9]开展了离心机模型试验,对Aydan等[8]提出的弯曲倾倒破坏分析方法进行了完善;Zhang等[10]将倾倒破坏边坡分区,提出了弯曲倾倒破坏分析的新方法;Amini等[11]提出了基于极限平衡理论的块状-弯曲倾倒破坏稳定性评价方法;孙朝燚等[12]提出了边坡滑动-块状倾倒-弯曲倾倒复合破坏的逐步分析方法;王俊杰等[13]基于叠合悬臂梁模型,改进了反倾岩层的极限平衡分析方法,推导了任意岩层下推力的理论公式。
目前倾倒破坏分析方法仍以极限平衡分析方法为主,对弯曲倾倒破坏分析方法的研究则集中在基于极限平衡理论的悬臂梁弯曲模型上。但现有弯曲倾倒分析方法大多将岩层按倾倒破坏模式进行分析,而未考虑到坡脚岩层的剪切破坏。工程实际中,该类边坡多为弯曲倾倒-剪切滑移复合破坏模式,故本文对弯曲倾倒-剪切滑移复合破坏模式的分析方法展开研究,以期为防治该类边坡破坏提供参考。
2 弯曲倾倒-剪切滑移破坏
当边坡坡体存在一组与边坡走向相近,且倾向坡内的主控裂隙组时,岩层在自重及层间力作用下易产生弯曲倾倒破坏。Adyan等[8]和Adhikary等[9]对这种破坏机制进行分析时,将岩层看作叠置的悬臂梁,通过岩层最大拉应力等于抗拉强度这一极限平衡条件,推导了相邻岩层间的层间作用力表达式,从边坡上部岩层开始,通过迭代计算得到坡脚处的剩余不平衡力,以剩余不平衡力的大小作为边坡稳定性的判据。
岩体的破坏形式通常为拉破坏或剪破坏,反倾边坡岩层的破坏形式应由岩层首先达到何种临界破坏状态来决定。Adyan等[8]和Adhikary等[9]在进行理论分析时,只考虑了岩层的弯曲拉裂破坏,而忽略了岩层可能的剪切破坏形式。实际上,在长细比较小的情况下,岩层具有较强的抗弯刚度,需要较大的推力才能使其产生弯曲倾倒破坏,如果此时岩层底面的剪应力超过了其抗剪强度,岩层其实已经产生剪切破坏。工程实例[14]及模型试验[15]均表明,弯曲倾倒破坏边坡内部的某些岩层实际产生的是剪切滑移破坏(见图1)。该类边坡的破坏应为弯曲倾倒-剪切滑移复合破坏模式,根据岩层变形破坏特征,可将其分为后缘稳定区、中部弯曲倾倒区和前缘剪切区3个区域,如图2所示。只考虑岩层的弯曲倾倒破坏将导致稳定性评价方面的偏差,本文将根据岩层的受力特征,对弯曲倾倒-剪切滑移破坏的边坡进行分析研究,并提出相应的稳定性分析计算方法。

图1 弯曲倾倒-剪切滑移破坏典型照片[14]
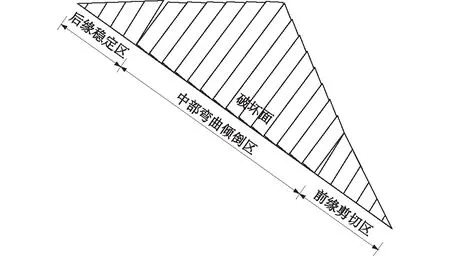
图2 弯曲倾倒-剪切滑移破坏示意图
3 弯曲倾倒-剪切滑移破坏分析方法
3.1 地质几何模型
建立如图3所示的等厚岩层反倾边坡的弯曲倾倒-剪切滑移破坏地质几何模型。图3中H为坡高;l为边坡坡面在层面法线上的投影长度;hm为坡顶岩层长度;t为岩层厚度;α为边坡坡角;β为岩层倾角;θ为破坏面沿层面法线偏转角度。
由几何关系可得
(1)
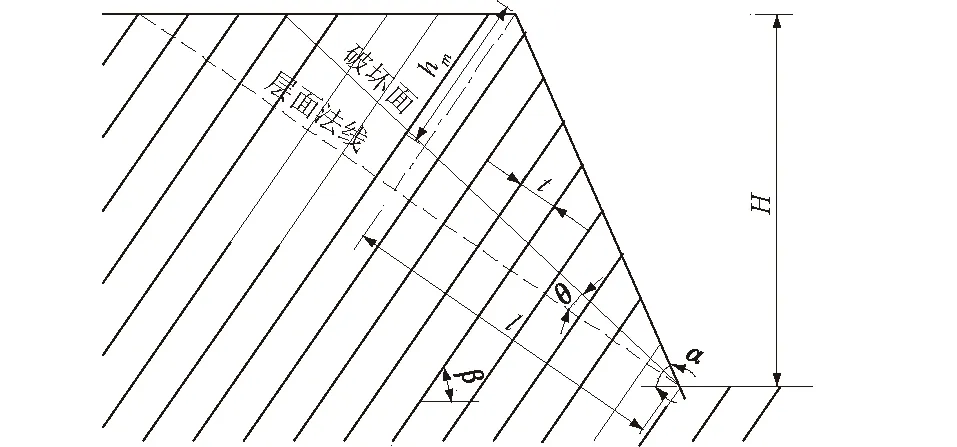
图3 地质几何模型
自下而上对岩层进行编号,坡脚岩层编号为1,则坡顶岩层编号m为
(2)
式中int为取整函数。
边坡岩层i破坏面以上的长度hi可表示为
(3)

图4 界限失稳长度分析
3.2 界限失稳长度与起始不稳定岩层
卢海峰等[16]指出,弯曲倾倒起始不稳定层是在自身重力作用下不稳定的岩层。以只受自身重力作用的岩层进行分析,当其处于弯曲倾倒极限平衡状态时,岩层的最大拉应力σmax等于岩体抗拉强度σt,将此时的岩层长度定义为界限失稳长度hlim,见图4。图4中W为岩层重力,N为轴力,M为弯矩,T为剪切力。
根据弹性理论,平面应变状态下,岩层的最大拉应力为
(4)
式中:N=Wsinβ,W=γth,h为岩层长度,γ为岩体重度;M=Wcosβ·h/2;A为岩层底面积;I为极惯性矩,I=t3/12。
可求得岩层最大拉应力表达式为
(5)
对弯曲倾倒极限平衡状态的岩层,岩层最大拉应力应满足σmax=σt,则可求得界限失稳长度hlim为
(6)
根据起始不稳定岩层长度与界限失稳长度的关系,hn≥hlim,可求出起始不稳定岩层的编号n,即
(7)
3.3 基本假定及力学模型
由于反倾岩质边坡坡体内部岩层受力状态较复杂,很难实现岩层弯矩的系统计算,需通过一定假设条件来简化分析过程。本文对弯曲倾倒-剪切滑移破坏进行分析计算时,沿用Adhikary等[9]提出的如下几条基本假设:①将相邻岩柱的法向作用力视为集中力,作用位置为χhi,χ为表征力的作用点位置的参数,χ∈(0,1);②破坏面为与岩层法线存在一定夹角的平面;③破坏面以上的岩层同时处于极限平衡状态。
对某一岩层,其在自身重力及层间力作用下产生哪种破坏模式是由岩层自身结构和受力特征决定的。根据不同的破坏模式,对岩层分别进行受力分析。
对岩层按弯曲倾倒破坏进行分析时,采用Adhikary等[9]的力学计算模型,如图5。图5中Pi、Pi-1为层间法向作用力,τi、τi-1为层间切向力,τi=Pitanφj,τi-1=Pi-1tanφj,φj为层面内摩擦角。

图5 弯曲倾倒力学模型[9]
在计算岩层底部轴力时,Adhikary等[9]未考虑层间切向力的影响,这将影响评价结果的准确性,本文予以考虑,则由静力平衡条件可得岩层底部轴力,为
N=Wisinβ+τi-τi-1。
(8)
式中Wi=γthi。
岩层所受各力对底部中心点取矩可得
(9)
当岩层处于极限平衡状态时,岩层最大拉应力应满足
(10)
将式(8)、式(9)代入式(10),并引入稳定性系数k,可得弯曲倾倒破坏极限平衡状态时的层间作用力表达式为
Pi-1=
(11)

图6 剪切滑移破坏 受力分析
对岩层按剪切滑移破坏进行分析,岩层受力分析如图6所示。图6中Qi、Qi-1为层间作用力。
根据静力平衡条件,可得
(12)
当岩层处于剪切破坏极限平衡状态时,岩层底面剪切应力等于岩体的抗剪强度,即
(13)

表1 皖南反倾边坡算例计算参数
式中:τ为剪切应力,τ=T/A,A为岩层底面积;φ为岩体内摩擦角;c为岩体黏聚力。
联立式(12)、式(13),可得剪切破坏极限平衡状态时的层间作用力表达式为
对以上求得的不同破坏模式下的层间作用力Pi-1和Qi-1进行分析,若某岩层Pi-1>Qi-1,表明该岩层在自重及层间力的作用力条件下首先达到弯曲倾倒极限平衡状态,此时岩层潜在破坏模式为弯曲倾倒破坏;若Pi-1=Qi-1,表明岩层同时处于弯曲倾倒和剪切极限平衡状态,岩层破坏为弯曲-剪切复合破坏模式;若Pi-1 从边坡起始不稳定岩层开始计算,得到岩层的弯曲倾倒极限平衡状态时的层间法向作用力Pi-1及剪切滑移极限平衡状态时的层间作用力Qi-1。当某一岩层的Pi-1≥Qi-1时,该岩层为弯曲倾倒或弯曲-剪切破坏,在下一步分析计算时,则以Pi-1作为该岩层与下部岩层的层间推力;当Pi-1 本文在稳定性计算时引入了稳定性系数k,以此作为边坡稳定性的评价标准。在以上计算过程中,令P0(Q0)=0,即可得到边坡的稳定性系数k。 为方便分析,定义量纲为1的参数,即剪切比例系数λ,其值为剪切破坏岩层数与破坏岩层总数的比值,即 (15) 式中:j为剪切破坏岩层数;s为破坏岩层总数,其大小等于起始不稳定岩层编号n。 上述推导了反倾岩质边坡弯曲倾倒-剪切滑移破坏的分析过程,以下以皖南反倾板岩边坡[14]工程实例验证本文所提出的分析方法。该边坡基岩为板桥组(Pt2b)砂质千枚状板岩,板岩岩体层面产状平均为NW31°/NE72°,板理面倾向坡内,在各种地质营力作用下发生了倾倒变形破坏,原始计算参数见表1。在分析计算时,应先确定层间力作用点位置以及破坏面位置,Adhikary等[9]的离心机模型试验结果表明岩质边坡岩层间的作用力近似均匀分布,即χ=0.5,本文算例分析中取χ=0.5,刘海军[14]的模拟分析表明,破坏面沿层面法线偏转角度θ约为5°,本文计算时取θ=5°。 采用以上分析方法,通过Excel规划求解工具进行计算分析,结果显示,边坡稳定性系数为0.961,边坡处于不稳定状态,边坡坡脚岩层为剪切滑移破坏(j=3),这与边坡实际已失稳破坏相符。而采用相同的计算参数,只考虑岩层弯曲倾倒破坏时,计算结果为P0=-6 290.63 kN<0,稳定性系数为1.20,说明边坡处于稳定状态。对比分析可见,对该类反倾岩质边坡单纯按弯曲倾倒破坏进行分析计算时,计算结果与工程实际存在出入,而本文提出的弯曲倾倒-剪切滑移破坏分析计算方法则与实际符合性较好。 为研究岩层倾角、边坡坡度、岩层厚度以及层面内摩擦角等对边坡稳定性系数k及剪切比例系数λ的影响,以上述皖南板岩边坡为算例进行分析讨论,参数分析情况如表2所示。 表2 参数分析 岩层倾角β对边坡稳定性系数k及剪切比例系数λ的影响如图7所示。从图7(a)可以看出,边坡稳定性系数随岩层倾角增大而减小,且边坡坡角越小,岩层倾角变化对稳定性系数的影响越显著。由图7(b)可见,在边坡坡角较小时,剪切比例系数随岩层倾角增大而减小的趋势较显著,而在边坡坡角较大时,岩层倾角对剪切比例系数影响较小,且保持在较低水平。图7(b)也可反映出,在边坡坡角较小时,随着岩层倾角增大,边坡破坏模式有由弯曲倾倒-剪切滑移向弯曲倾倒转变的趋势。 图7 不同坡角时β-k、β-λ关系曲线 图8(a)为边坡坡角对边坡稳定性系数的影响曲线,由图8(a)可见,边坡稳定性系数随边坡坡角增大而减小,这与岩层倾角变化对边坡稳定性系数的影响相似,但对比图7(a)和图8(a)可看出,稳定性系数随坡角变化幅度大于其随岩层倾角变化幅度,表明边坡坡角变化对边坡稳定性的影响要大于岩层倾角的影响。图8(b)为边坡坡角对剪切比例系数的影响曲线,可见,剪切比例系数随边坡坡角增大而减小,且在岩层倾角较小时变化明显,表明随边坡坡角增大,边坡剪切破坏岩层范围不断减小。 图8 不同岩层倾角时α-k、α-λ关系曲线 图9 岩层厚度和层面内摩擦角对k及λ的影响 图9(a)反映岩层厚度对边坡稳定性系数及剪切比例系数的影响。由图9(a)可知,稳定性系数及剪切比例系数均与岩层厚度呈正相关关系,均随着岩层厚度的增加线性增长,表明随着岩层厚度的增加,坡脚剪切滑移区范围扩大,产生剪切滑移的岩层数增多。这是因为岩层厚度增加增强了岩层的抗弯刚度,而对剪切强度影响很小,使得容易产生剪切破坏的岩层数增多,从而导致了剪切比例系数的增加。 岩层内摩擦角对边坡稳定性系数及剪切比例系数的影响如图9(b)所示,可见边坡稳定性系数及剪切比例系数均随内摩擦角增加而增大,且近似呈线性关系。层面内摩擦角的增加提高了岩层的抗弯弯矩,减少了弯曲倾倒岩层数,而对剪切滑移岩层数影响不大。对比图9(a)、图9(b)可发现,剪切比例系数随层厚变化趋势大于随层面内摩擦角变化趋势,表明层厚对剪切破坏区范围的影响大于层面内摩擦角的影响。 (1)岩质边坡弯曲倾倒破坏,边坡坡脚往往产生的是剪切破坏,该类边坡的破坏为弯曲倾倒-剪切滑移复合破坏模式,根据岩层变形破坏特征,可将边坡分为后缘稳定区、中部弯曲倾倒区和前缘剪切区3个区域。 (2)工程实例验证表明,未考虑岩层剪切破坏将导致稳定性评价方面的偏差,而弯曲倾倒-剪切滑移破坏计算模型分析结果则与工程实际吻合性较好。 (3)岩层倾角越陡、坡角越大,边坡稳定性越差,且坡角对边坡稳定性的影响大于岩层倾角的影响;边坡稳定性系数随岩层厚度及层面内摩擦角的增加线性增长,而层厚对剪切破坏区范围的影响大于层面内摩擦角的影响。4 工程实例验证
5 参数分析与讨论
5.1 岩层倾角β对k及λ的影响

5.2 边坡坡角α对k及λ的影响

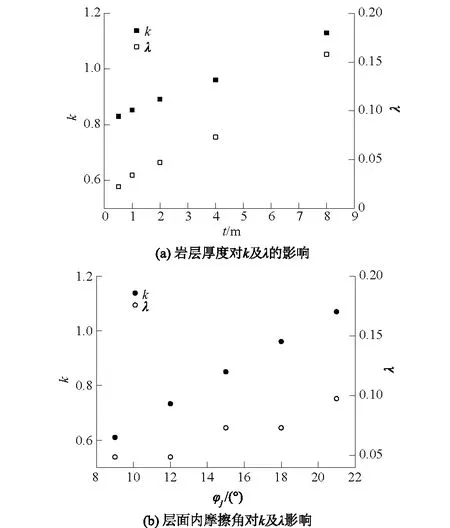
5.3 岩层厚度t对k及λ的影响
5.4 层面内摩擦角φj对k及λ的影响
6 结 论
