基于HYDRUS-1D模拟的降雨入渗条件下VG模型参数敏感性分析
2021-07-12
(北京林业大学 水土保持学院,北京 100083)
1 研究背景
土壤水分入渗是指水由土壤表面渗入土壤内部的过程,是土壤水分运动中心环节[1],研究土壤水分入渗规律对合理利用水资源,指导农林业生产具有重要意义。相比于耗时长、花费大的传统田间试验,精确的数值模型模拟能够极大提高工作效率。基于Richards原理的HYDRUS-1D模型因其模拟结果的准确性和广泛的适用性,再加上便捷灵活的操作及集成参数优化功能而被广泛应用于土壤水分运动研究中[2-4]。大量学者通过试验数据与模拟数据的对比发现此模型在土壤水分运动研究中具有很好的适应性[5-9]。实际模拟过程中,模拟参数的确定往往是最关键的环节,参数的准确性直接影响着模型率定效率以及模型输出结果的可靠性[10-11]。因此,对土壤水力参数进行敏感性分析,明确参数扰动对入渗特性的影响规律,有助于提高模型模拟精度,便于更加高效的应用。
模型的模拟精度除受到模型参数变化的影响外,外界输入条件也不可忽略[12]。已有的相关研究主要集中于定水头入渗条件下的参数变化对输出结果的影响,如王志涛等[13]分析了Van Genuchten模型(简称VG模型)参数变化对粉壤土入渗特性的影响;范严伟等[14]研究定水头入渗情况下HYDRUS模型土壤水力参数变化对不同质地土壤入渗特性的影响;刘钢等[15]研究发现饱和含水量θs、饱和导水率Ks、进气吸力倒数α和孔隙尺寸分布指数n这4个参数对压力水头和溶质运移的影响较为显著;霍思远等[16]研究表明针对不同的输出结果参数敏感性不同,并提出参数敏感性分析及调参过程应结合土壤参数的物理意义展开。以上研究多在定水头入渗条件下进行,未考虑到降雨入渗作为边界条件的情况。相比于定水头入渗,自然降雨下的入渗过程更符合实际情况,研究结果也更有助于实际应用。张海阔等[17]以南京市2 a一遇设计暴雨过程作为上边界输入条件,主要在土层的垂直方向及水平方向研究参数扰动对输出结果的影响。其结果表明降雨入渗条件下土壤水力参数扰动对入渗规律的影响与定水头研究结果有较大差异。目前尚无降雨入渗条件下,参数扰动对入渗随时间变化过程的影响研究。
本研究以北京市2 a一遇设计暴雨过程为例作为上边界输入条件,选取HYDRUS-1D模型中的5个土壤水力参数(θs、Ks、α、n、残余含水量θr),研究前锋雨型下单因素扰动对地表10 cm层土壤水分动态分布、累积入渗量及湿润锋运移距离的影响,针对不同的输出结果分析参数的敏感性。旨在完善降雨入渗条件下HYDRUS-1D模型参数敏感性研究规律,量化参数敏感性对于不同输出结果的影响,明确参数敏感性随时间变化规律,以便在实际应用中注意高敏感性参数的精度对模拟结果的影响,提高模拟结果的准确性及模型使用的效率。
2 模型原理及模型设计
2.1 模型原理
HYDRUS-1D模型仅考虑一维垂向运移时的土壤水分运动[18],采用Richards方程描述一维非饱和土壤水流的运动,即
(1)
式中:t为时间(d);h为压力水头(cm);θ为土壤体积含水率;z为垂向空间坐标(cm);K(h)为非饱和导水率(cm/d);s(z,t)为根系吸水速率(cm/d)。
该方程是由达西定律和质量守恒定律推导而来,对于土壤水分运动过程的描述更加准确,更适合分析土壤水分动态变化特征。
本文使用应用广泛的VG模型拟合土壤水分特征曲线θ(h)和非饱和导水率K(h),其方程为:
(2)
(3)
其中,
(4)
式中:m为经验参数,n>1,m=1-1/n;l为经验参数,取0.5。
2.2 数值模型设计
2.2.1 离散化
模拟土层为均质土层,土壤类型选用软件内置壤土,土壤水力参数见图1。模拟土柱高度为100 cm,采用等间隔剖分方式将包气带分成100份。模拟时长共计24 h,模拟开始时设置2 h降雨条件。
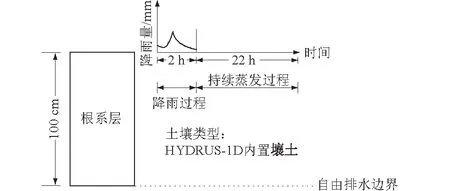
图1 模拟土柱示意图
2.2.2 初始及边界条件
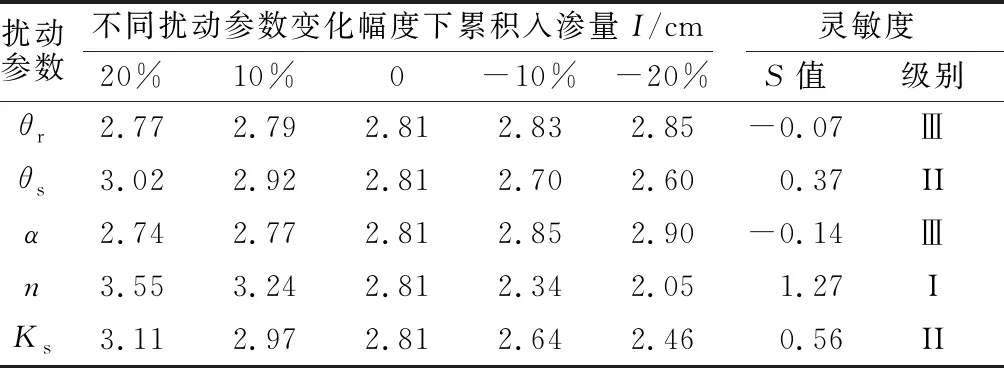
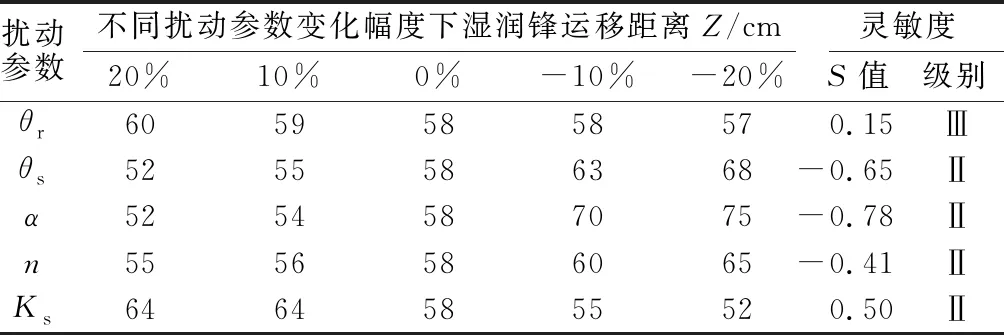
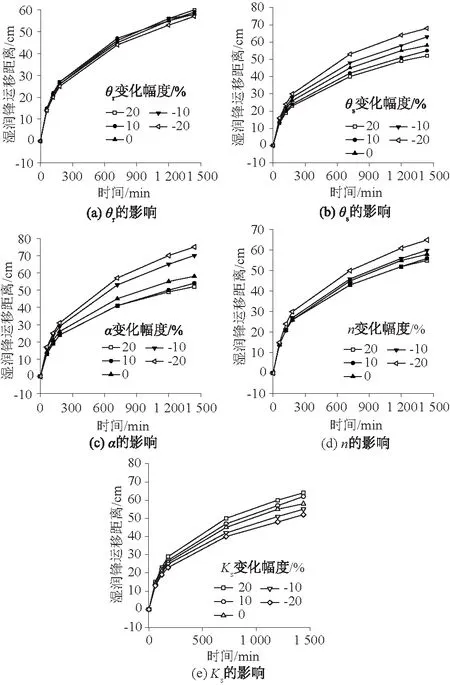
模型通过循环迭代计算获取稳定剖面含水率分布作为初始条件。下边界选择自由排水边界。在短历时暴雨雨型设计方面,芝加哥雨型在国内外应用广泛[19]。利用北京市II区新暴雨公式推求北京市2 a一遇设计暴雨量,降雨历时选用120 min,根据王彬雁等[20]的研究,北京市80%以上的雨型为单峰型,且在北京市单峰雨型中,雨峰位于前中后的比例差别不大。故本研究只针对单峰型雨型进行模拟,给定雨峰相对位置r(0 (5) 式中:q为设计暴雨强度(L/(s·hm2));t为降雨历时,取120 min;P为重现期,本研究以2 a一遇设计暴雨为例。北京市II区的P和t满足2 a≤P≤100 a,5 北京市II 区2 a一遇芝加哥雨型推求的暴雨过程如图2所示。 图2 北京市II 区2 a一遇芝加哥雨型过程 2.2.3 扰动参数设置 由模型原理可知,HYDRUS-1D模型的土壤水力参数主要有残余含水量θr、饱和含水量θs、饱和导水率Ks、进气吸力倒数α和孔隙尺寸分布指数n,同时这5个参数也是应用模型时需要输入的主要的土壤参数。采用HYDRUS-1D模型中壤土的设定值作为标准参数,各参数均以10%为步长,共分5种情况进行上下扰动,各情况对应的参数设置见表1,根据前人相关研究可知各参数20%的增减变化幅度处于合理范围内。 表1 土壤水力参数扰动结果 2.2.4 输出变量 分别选择HYDRUS-1D模型中t=120 min时的累积入渗量、地面10 cm层的土壤水分动态分布及湿润锋运移距离为研究对象,分析参数扰动对降雨结束后累积入渗量、地面10 cm深度的土壤水分动态分布及湿润锋运移距离的影响。 Morris[21]提出的筛选法是一种运算简单且效率较高的敏感性分析方法,被广泛应用于各种水文模型中,本文采用修正的Morris筛选法对HYDRUS-1D模型参数进行敏感性分析,参数灵敏度取多次扰动所计算出的Morris系数的平均值,即 (6) 式中:S为参数灵敏度;N为模型运行次数;Yi为第i次运行后模型的输出值;Yi+1为第i+1次运行后模型的输出值;Y0为模型计算结果的初始值;Pi为模型第i次运行时参数取值相对于初始值变化的百分率;Pi+1为模型第i+1次运行时参数取值相对于初始值变化的百分率;P0为参数初始取值。 参数敏感度分级如表2所示。 表2 参数敏感度分级 土壤含水量的变化与降雨过程相关程度较高,尤其是表层土壤含水量的变化[1]。本研究借助10 cm处土壤含水量的变化来反映表层土壤水分动态变化。从图3可以看出,表层土壤含水量随降雨时间的增加迅速增加,降雨结束时达到最大。随后,表层水分向深层迁移,表层含水量逐渐减少。各土壤水力参数对水分特征曲线及非饱和导水率影响程度不同是导致参数敏感性差异的主要原因。 图3 10 cm层土壤含水量动态分布 图4 参数扰动对10 cm层土壤含水量分布的影响程度 从图4可知,α、Ks、n扰动的敏感性均在雨峰后(t=50 min)达到最大,θr在t=40 min时达到最大,降雨结束后其敏感性均降低。α、Ks在降雨结束后,其|S|值均<0.05,敏感性级别为IV;θr在降雨结束后其敏感性也显著降低,|S|值略>0.05。这说明降雨结束后θr、α、Ks扰动对10 cm层土壤水分动态分布基本无太大影响。而θs扰动在降雨开始后达到一个次峰值(|S|值为0.83),经历一个短暂的下降后增加至峰值(|S|值为0.95)并保持微弱的浮动,说明θs扰动在整个10 cm层土壤水分动态分布过程中,均具有较大影响。参数n的敏感性在降雨50 min时达到最大,其|S|值为1.37,敏感性级别为Ⅰ,随后其敏感性急速下降,并随后续的入渗过程呈现一个较缓的增长。5个参数对10 cm层土壤水分动态分布的敏感性最值排序为n>θs>α>Ks>θr,其敏感度级别分别为Ⅰ、Ⅱ、Ⅱ、Ⅱ、Ⅱ。此外,从图3还可以看出,θr和θs扰动与10 cm层土壤含水量动态分布的变化呈正相关关系,而α、n、Ks扰动与10 cm层土壤含水量动态分布的变化呈负相关关系。 以上结果说明参数的敏感性并不是一个恒定不变的,不同的研究时段下参数敏感性不同,根据研究需要确定参数敏感性变化区间对简化试验工作具有重要意义。如在模拟分析10 cm层土壤水分动态分布规律时,应尽可能确保n、α、θs及Ks参数的准确性,在分析降雨前后10 cm层土壤水分动态分布规律时,应尤其注意θs参数的准确性。因此,参数敏感性随时间的变化也应该作为模型模拟时需要考虑的因素之一。 根据表3可以看出,5个参数扰动累积入渗量的敏感性排序为n>Ks>θs>α>θr,其敏感性级别分别为Ⅰ、Ⅱ、Ⅱ、Ⅲ、Ⅲ。其中θr扰动对累积入渗量的影响很小,其|S|值仅为0.07。而θs、n、Ks的扰动对累积入渗量的影响很大,尤其是参数n,其|S|值为1.27。因此,在模拟分析累积入渗量时,应尤其注意θs、n、Ks这3个参数的准确性。 表3 参数扰动对累积入渗量的影响 此外,还可看出α与θr扰动与累积入渗量的变化呈负相关关系,θs、n、Ks扰动与累积入渗量的变化呈正相关关系。此结论与前人定水头研究结果不同,如范严伟等[14]认为θs扰动与累计入渗量变化呈负相关关系,而本研究发现为正相关关系,本研究结果与张海阔等[17]的结论一致。 定量分析t=1 440 min时,各参数扰动对湿润锋运移距离的影响,并计算相应的灵敏度,如表4所示。 表4 参数扰动对湿润锋运移距离的影响 从表4可知,5个参数对湿润锋运移距离的敏感性排序为α>θs>Ks>n>θr,其敏感性级别分别为Ⅱ、Ⅱ、Ⅱ、Ⅱ、Ⅲ。θr扰动对湿润锋运移距离的影响较小。而θs、α、n及Ks扰动对湿润锋运移距离的影响均较大,其|S|值分别为0.65、0.78、0.41、0.50。因此在模拟分析湿润锋运移距离时应尽可能确保θs、α、n及Ks这4个参数的准确性。此外,θs、α、n的扰动与湿润锋运移距离呈负相关关系,Ks及θr扰动与湿润锋运移距离呈正相关关系。该结论与定水头条件下的研究结果并不一致。如范严伟等[14]研究发现在定水头输入条件下n与湿润锋运移距离呈正相关,本研究为负相关。 从图5可以看出,不同参数扰动下的土壤湿润深度随时间的变化规律类似。土壤的湿润深度随降雨过程时间增加基本呈线性增加,随后在土壤水分重力和毛管孔隙的作用下,土壤湿润深度随湿润锋向深层运移而增加,增速较降雨期间减缓。 图5 土壤湿润锋运移距离随时间的变化 结合累积入渗量及湿润锋运移距离的研究结果,对比前人定水头的研究结果可知,不同的边界条件下模型输出结果不同。即边界条件也是影响模型模拟结果的重要因素之一,因此在模型模拟时应根据实际情况选择合适的边界条件。 水文模型的使用可极大的提高工作效率,但一般而言,水文模型通常会涉及到很多参数的输入,由于对水文模型机理的认知不足或参数本身难以通过试验确定等原因,通常很难做到同时提高很多参数的精度,输入参数的不确定性往往会对模拟结果产生较大影响。参数敏感性分析的目的就是确定输入参数对结果的影响程度,从而可以降低参数率定过程中的计算消耗,提高模型的量化能力,降低参数维数等以提高模型使用效率。 在参数敏感性分析方面有大量的研究方法[22-23],本文采用最常用的Morris筛选法进行分析。在应用HYDRUS-1D模型进行模拟时,模型参数的准确性及边界条件会对输出结果产生较大影响。因此对不同的受影响研究对象开展参数的敏感性研究有助于简化后续的参数率定工作,提高模型应用效率及模拟精度。 关于HYDRUS-1D模型参数的敏感性,前人的研究多集中在定水头输入条件下[15-18],本研究则以降雨入渗作为边界条件,以10 cm层土壤水分动态分布、累积入渗量和湿润锋运移距离为受影响研究对象,研究了其随5个主要土壤水力参数变化的敏感性规律,研究结果丰富了降雨入渗条件下HYDRUS-1D模型参数敏感性结果,对于模型的使用效率及模拟结果准确性的提高具有实践指导意义。 模型参数的确定应根据其物理意义具体问题具体分析。θs可通过实验准确测定,因此可将θs取为实测值,从而避免VG模型参数确定过程中θs的误差。有研究表明饱和导水率Ks与土壤基本性质之间存在一定关系,因此可通过土壤质地或土壤粒径分析等土壤理化参数,建立土壤转换函数,估算或预测Ks的空间分布。α是土壤进气值的倒数,在实际应用中可提前给出α的取值范围,根据多次迭代拟合确定。n与土壤粒径分布有关,n值的确定方法与α类似。 笔者建议,在应用HYDRUS-1D模型进行模拟前可针对拟输出结果进行参数敏感性分析,明确相应参数的敏感性程度或高敏感性区间,进而减少敏感性低的参数的试验确定工作,提高工作效率。本研究的土壤类型为软件内置壤土,土层为均质土层,未考虑土壤大孔隙及层状土体结构对土壤水分运移的影响。且模型上边界条件为2 a一遇芝加哥雨型,与实际降雨过程可能有一定差异。后续研究者可结合实测土壤入渗数据及土层条件进行深入研究,从实测数据与模拟数据的拟合角度去进一步分析参数敏感性对于模型应用的具体影响。 降雨入渗条件下,5个参数扰动对HYDRUS-1D模型输出结果的敏感性存在如下规律: (1)模型参数的敏感性并非一成不变,针对不同的输出结果,参数敏感性随时间变化规律不同。根据研究需要确定参数敏感性区间对简化试验工作具有重要意义。 (2)边界条件也是影响模型参数敏感性的重要因素之一,不同的边界条件会对输出结果产生较大影响,因此在模型模拟时应力求边界条件的真实性。 (3)对于不同的受影响研究对象,5个参数的敏感性不同。如n、α、θs及Ks这4个参数对10 cm层水分动态分布影响较大,θs、n、Ks对累积入渗量影响显著。θs、α、n及Ks对湿润锋运移距离的影响较大。模拟时应确保高敏感性参数的准确性。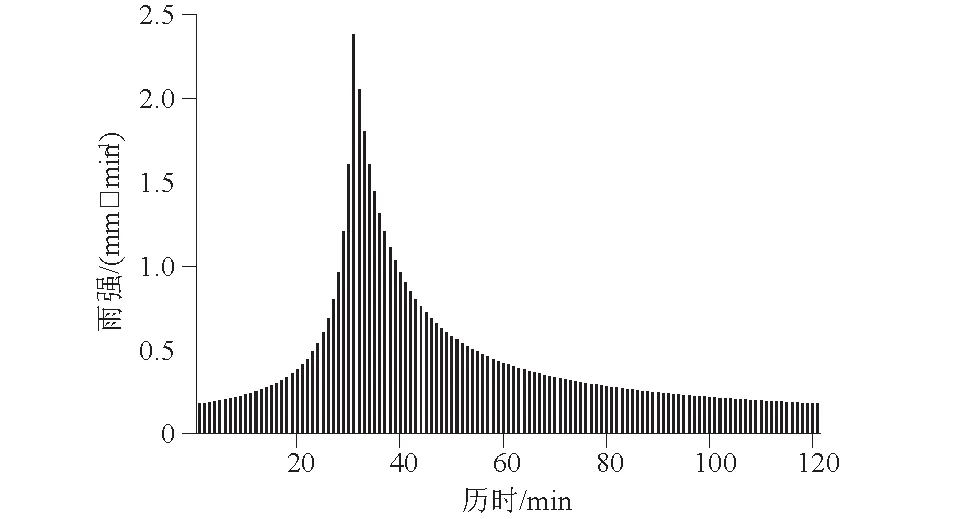

3 土壤水力参数对计算结果的影响分析
3.1 分析方法

3.2 土壤水力参数对10 cm层土壤含水量动态分布的影响


3.3 土壤水力参数对累积入渗量的影响
3.4 土壤水力参数对湿润锋运移距离的影响
4 讨 论
5 结 论
