孤立波作用下斜坡堤越浪量的数值模拟
2021-07-12魏斐斐熊芳杰任兴月
魏斐斐, 熊芳杰, 任兴月
(海南大学土木建筑工程学院, 海口 570228)
海啸是由海底地震、火山爆发、海底滑坡或气象变化产生的破坏性海浪,全球有记载的破坏性海啸约260次,造成重大灾难,也引起中外众多学者对海啸的研究。海啸在到达近海岸时,波浪越高,越容易越过斜坡堤,越浪量的大小也就决定着是否会对近海岸造成危害。孤立波与海啸的波形极其相似,常被用来模拟海啸等浅水大波[1]对海岸建筑物的破坏。所以,研究孤立波作用下斜坡堤越浪量的数值模拟,具有重要的学术意义和一定的工程应用价值。
中外众多学者对规则波和不规则波在防波堤作用下的越浪进行了研究。Tofany等[2]采用数值方法研究了规则波对垂直防波堤越浪和冲刷的影响,周雅等[3]通过波浪断面物理模型研究了不规则波作用下斜坡堤的越浪量,并比较了随机、规则两种扭王字块体摆放形式的消浪结果;Guo等[4]研究了非破碎波和破碎波两种情况下海堤上越浪流动特征,得到了越浪量与堤顶最大流速之间的关系;张淑华等[5]利用设置造波边界法和质量源法,模拟线性波和二阶Stokes波与建筑物的爬高,与理论解拟合结果较好。防堤坡的种类也是影响越浪量的重要因素。朱伟娜[6]针对中国常见的坡面带栅栏板和块体的斜坡堤,进行越浪量物理模型试验,分析海堤顶流特征参数的分布规律。王键等[7]通过模拟不同断面尺寸的带胸墙斜坡堤越浪,分析了不同斜坡堤相关因素对平均越浪量的影响。
较多学者对孤立波与结构物的相互作用进行了研究。Hsiao等[8]利用孤立波对斜坡堤作用的实验,研究了孤立波越过海堤、在海堤上坍塌、在海堤后坍塌三种情形下波高、荷载的变化。Ji等[9]以数值模拟的方法研究了斜坡海滩上不透水的梯形海堤在孤立波冲击下的水动力特性,以及波浪参数对海堤水动力稳定性的影响。Xuan等[10]在波浪水槽中进行了平面海滩上双孤立波的冲高实验,给出相对波峰分离距离对孤立波爬高的影响。但他们均未对孤立波在爬高产生的越浪量进行深入研究。为了研究孤立波对斜坡堤越浪的情况,张金牛等[1]在波浪水槽中进行了孤立波在斜坡堤上越浪的实验,分析了相对波高、相对超高对越浪量的影响,但未考虑堤顶宽度的影响因素;曾婧扬等[11]用Goring造波方法建立了二维数值波浪水槽,进行孤立波在简单斜坡堤越浪的数值模拟,分析了相对堤顶宽度和相对波高对越浪量的影响,并得出堤顶流最大厚度分布及最大速度分布公式,但未考虑到相对超高对越浪量的影响。
主要以孤立波作用下斜坡堤的越浪量问题展开研究,基于FLUENT软件,采用速度边界造波,并编写了孤立波速度入口的用户定义函数(user defined function,UDF)程序,流体体积函数(volume of fluid,VOF)方法追踪自由表面,建立二维数值波浪水槽。通过与文献[1]物理模型实验结果对比,验证了该数值波浪水槽的有效性。进而研究了相对波高、相对超高、相对堤顶宽度对孤立波在斜坡堤上越浪量的影响,并总结出孤立波越浪量沿堤顶宽度衰减的经验公式。
1 数值模型
1.1 控制方程
采用二维两相流模型,介质为不可压缩均质流体水和空气,连续方程为
(1)
纳维-斯托克斯(N-S)方程为
(2)
(3)
式中:t为时间;(x,y)为笛卡尔坐标系;u为流体质点速度;ux和uy分别为流体质点在x和y方向的速度;∇2为拉普拉斯算符;p为大气压强;ρ为流体密度;fx和fy为x、y方向上的黏性力项。
1.2 孤立波在数值水槽的验证
三阶孤立波公式为[12]
(4)
(5)
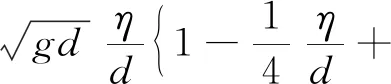
(6)

(7)
(8)
(9)
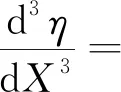
(10)
式中:c为波速;g为重力加速度;d为水深;H为波高;η为孤立波的波面方程的波面高度;X=x-ct;u和w分别为孤立波水平速度和竖直速度;(x,z)为平面坐标系。
为了验证数值造波的有效性,采用了文献[1]中前三组物模实验数据(表1),在30 m×1.2 m无防堤坡平底水槽中进行波高随时间t的数值模拟。入口边界采用UDF造波,程序中运用DEFINE_PROFILE宏和式(6)、式(7)进行边界速度造波编译,出口边界为压力出口边界,上边界为对称边界。网格划分采用0.05 m均匀结构化网格。取x=10 m处的波面变化,数值模拟结果和理论值对比如图1所示。由图1可知,不同波高的数值模拟的结果和理论值均基本吻合,说明孤立波的速度造波方法在数值波浪水槽中的可行性。

表1 孤立波验证参数Table 1 Parameters of solitary wave
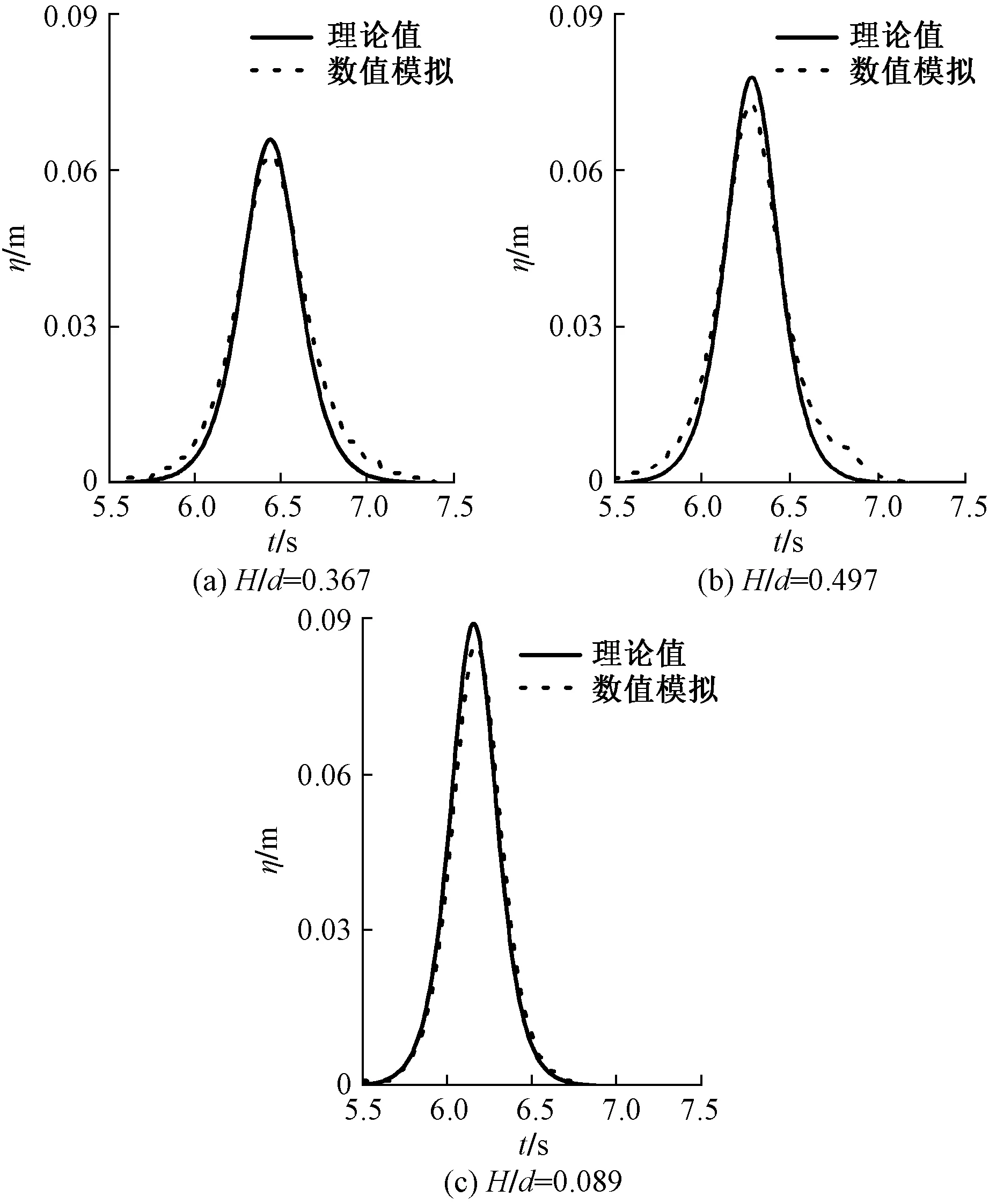
图1 数值水槽造波与理论波形的比较Fig.1 Comparison of wave profile with numerical wave flume and theory
2 斜坡堤越浪数值模拟
2.1 越浪量模拟值与实验值对比
中外斜坡式防堤坡越浪量计算方法不同,李社生等[13]利用2D防堤坡越浪物理模型实验对不同方法进行了计算。范红霞[14]通过物理模型实验,分析各种因素对越浪量的影响,建立了适用中国海堤结构的平均越浪量计算公式。基于FLUENT软件,提出孤立波越浪量数值模拟的计算方法。利用VOF自由表面追踪法,得到斜坡堤堤顶越浪的质量流速图,引入孤立波在净水平面以上的单宽水体体积q0,最终计算出无量纲单宽越浪量q*。
由孤立波波面方程[式(6)]可得
(11)
无量纲单宽越浪量q*计算公式为
(12)
式(12)中:m为数值模拟越浪量总质量,kg,即斜坡堤堤顶越浪的质量流速积分值;ρwater为水的密度,1×103kg/m3;b为单位宽度,b=1 m;q为数值模拟单宽越浪量。
2.1.1 网格的划分
为了准确捕捉自由表面的运动,提高对斜坡堤越浪过程及质量流速的模拟精度,计算中对水体表面和斜坡堤附近进行了网格的加密,如图2所示。
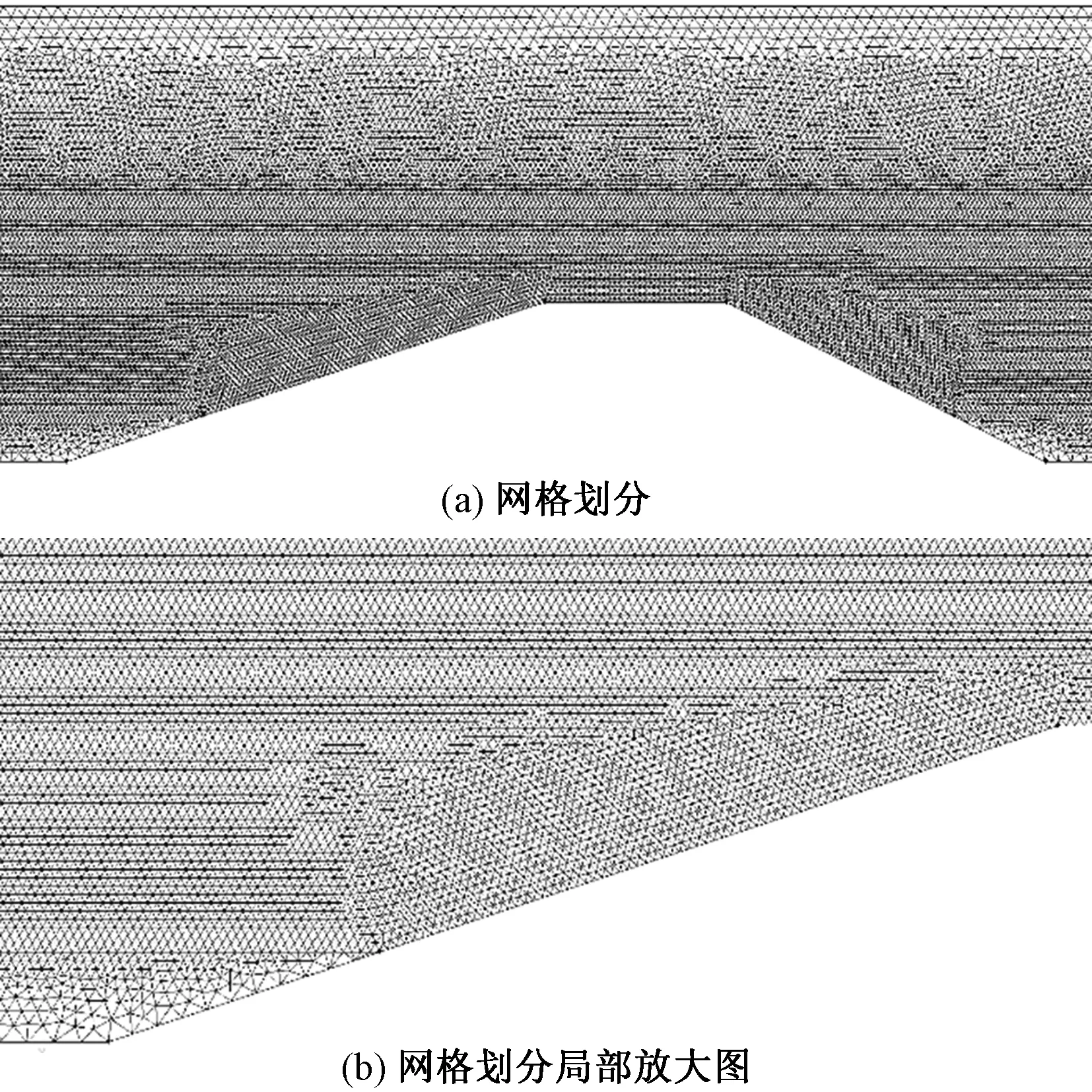
图2 模型网格划分Fig.2 Mesh of the numerical model
(1)竖直方向上:工况中最大波高为0.094 m,以静水面为基准,基准面-0.13 m为底,基准面+0.23 m为顶,此区域网格Δz=0.01 m,其余区域z方向上的网格大小Δz=0.03 m。
(2)水平方向上: 为了提高斜坡堤附近的计算精度,对斜坡堤堤前至堤后区域进行了加密,取Δx=0.01 m,其余区域x方向网格大小Δx=0.03 m。
图2(a)为斜坡堤附近网格划分,可以明显看出在斜坡堤中间及前后区域网格较密,其余地方较稀疏。图2(b)为斜坡堤前坡的网格放大图,采用三角形非结构性网格,可以使斜坡堤的斜面较好的均匀划分网格。
2.1.2 越浪量数值模拟计算结果分析
数值波浪水槽如图3所示,左侧造波边界采用UDF速度造波,右侧出口边界为压力出口,在斜坡堤后25~30 m范围内设置消波区,防止出口边界波浪反射对越浪量造成影响。图3中,斜坡堤前坡比为1∶3,后坡比为1∶2,d为水深,H为波高,堤顶宽度B=0.4 m,Rc为堤顶超高。通过改变水深和波高,共设计了16种与文献[1]相同的工况,详细参数如表2所示。FLUENT中设置堤顶最右端为积分面,选择x方向的质量流速,得到越浪的质量流速图,如图4~图7所示。运用式(11)、式(12)对不同水深不同波高进行越浪量计算,得出数值模拟的无量纲越浪量q*,并与文献[1]的实验值做对比。图8(a)为孤立波越浪量实验值和数值模拟值的比较,越浪量的数值模拟结果和计算结果较吻合,验证了数值波浪水槽的有效性。

图3 数值水槽及变量定义示意图Fig.3 Sketch of numerical flume and variable definition

图4 d=0.22 m越浪质量流速Fig.4 Mass flow rate on overtopping at d=0.22 m
从图4可以看出,相对波高(H/d=0.218,H/d=0.265)较小时,越浪波动较大,质量流速有明显的起伏,相对波高(H/d=0.345,H/d=0.393)较大时,质量流速曲线趋于光滑,没有较大的波动起伏。水深d=0.24、0.26、0.30 m有相似的现象,说明相对波高越大,质量流速变化越稳定。
Baldock等[15]通过物理模型实验,研究了孤立波爬高和越浪过程,提出孤立波爬高和越浪量经验公式为
(13)
(14)
式中:R表示孤立波前沿的爬高。
图8(b)为数值模拟越浪量值与文献[15]计算值的比较,数值模拟值比较接近文献[15]计算值,说明数值模拟的结果较好。
2.2 相对波高及相对超高对越浪的影响
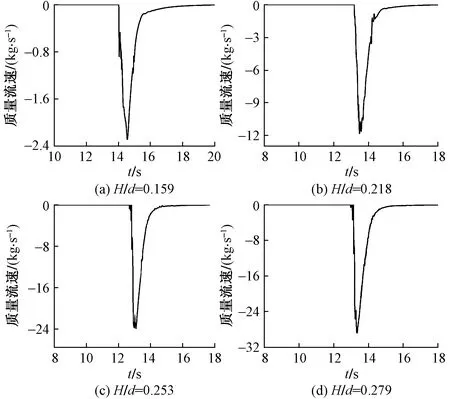
图5 d=0.24 m越浪质量流速Fig.5 Mass flow rate on overtopping at d=0.24 m

图6 d=0.26 m越浪质量流速Fig.6 Mass flow rate on overtopping at d=0.26 m

图7 d=0.30 m越浪质量流速Fig.7 Mass flow rate on overtopping at d=0.30 m

图8 孤立波越浪量数值模拟值与实验值及 文献[15]的计算值的比较Fig.8 Comparison of numerical simulation value of solitary wave overtopping with experimental value and calculated value in reference[15]
由于海啸巨大的破坏作用,学者们对孤立波的越浪量问题已经进行了大量的研究。发现越浪量的影响因素主要有海堤断面形式(防坡堤的结构形式、堤顶超高、平台宽度、防坡堤坡度)、波浪要素(波高、水深、周期)以及海面上的风速、海底地形等。郭立栋等[16]探讨了斜坡堤断面形式和波浪要素对越浪量的影响,发现相对胸墙高度与越浪量系数存在指数反比关系。常江等[17]通过物理模型实验,分析了堤顶宽度对越浪量的影响,给出了堤顶宽度对越浪量衰减系数的影响关系式。选择海堤断面形式中的相对超高、堤顶宽度和波浪要素中的相对波高3个因素,研究对孤立波越浪量的影响。
从图9(a)可以看出,相同水深,无量纲越浪量随着相对波高的增加而增大;在相同的相对波高下,孤立波的越浪量随着水深的增大而增加。但是不同水深的越浪量随相对波高增长的梯度不同。当d=0.22 m时,越浪量增长曲线在末端出现转折,曲线增长梯度减小。随着水深的增加(d=0.24 m、d=0.26 m、d=0.30 m),越浪量曲线未出现转折,且增长梯度也大于水深d=0.22 m的情况。关于较大水深的越浪量转折点是否出现在较大的相对波高处,可以通过更多数据来验证。
图9(b)为不同水深条件下相对超高对越浪量的影响。由图可以看出,相同水深时,相对超高越大,无量纲越浪量越小;在相同超高情况下,无量纲越浪量随着水深的减小而增大。从越浪量的增长趋势可以看出,水深d=0.22 m、d=0.24 m、d=0.26 m时,越浪量随着相对超高的减小梯度大致相同;d=0.3 m时,越浪量随着相对超高的减小梯度明显大于较小水深。
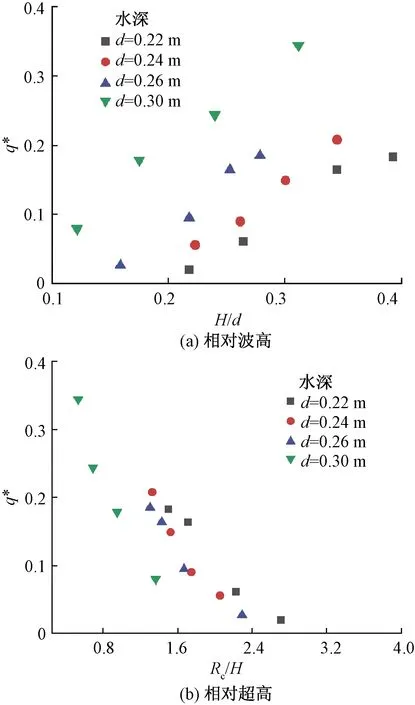
图9 相对波高、相对超高对越浪量的影响Fig.9 Effect of relative wave height, relative crest height on overtopping discharge
2.3 相对堤顶宽度对越浪的影响
由式(14)可得孤立波的越浪量影响因素有波高、水深、堤顶超高,未提及堤顶宽度B,而且Baldock等[15]和张金牛等[1]均未考虑堤顶宽度对越浪量的影响,但通过改变堤顶宽度的大小,发现堤顶宽度对越浪量有着很大的影响。Besley[18]通过对常规防堤坡越浪量的实验研究,提出越浪量沿堤顶宽度衰减的经验公式
(15)
式(15)中:Cr为衰减系数,定义为不同堤顶宽度的越浪量比值;A、K为常数。
为了研究堤顶宽度对越浪量的影响,增加工况20~工况23(表3)与工况4~工况7(表2)进行对比,表3中堤顶宽度为0.6 m,波高、水深、堤顶超高与工况4~工况7相同。通过对不同堤顶宽度的无量纲越浪量计算得出B/H与lnCr关系图(图10),从图10可知,堤顶宽度越大,越浪量越小。堤顶宽度B=0.6 m与B=0.4 m的越浪量衰减经验公式为

表3 不同堤顶宽度的数值模拟参数Table 3 Numerical simulation parameters of different levee crown width
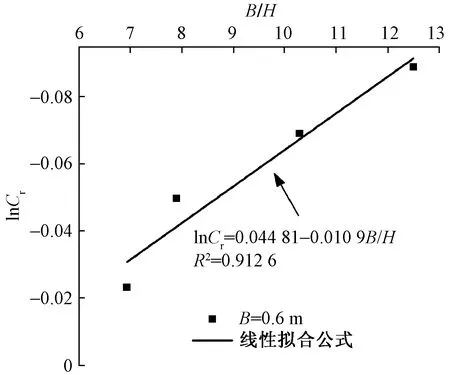
图10 越浪量衰减程度随堤顶宽度的变化Fig.10 Attenuation degree of overtopping with the width of embankment top
(16)
3 结论
基于所建立的孤立波-防波堤相互作用的二维数值模型,研究了相对波高、相对超高、堤顶宽度对孤立波越浪量的影响,得出如下结论。
(1)建立的孤立波数值模拟与理论值吻合较好,说明本文模型合理可靠。
(2)越浪量随着相对波高的增大而增大,随着相对超高、堤顶宽度的增大而减小。
(3)通过数值模拟的越浪量与实测值、文献[15]计算值比较,结果表明数值模拟的结果与实测值吻合较好,并且更接近文献[15]计算值。
(4)改变堤顶宽度,得出越浪量沿堤顶宽度衰减的经验公式。研究成果对孤立波在斜坡堤作用下的越浪量数值模拟具有一定理论分析和参考价值。
