基于统计学的再生沥青混合料疲劳性能试验研究
2021-07-12胡江三陆佳宝王国忠
胡江三, 陆佳宝, 王国忠, 屈 冉
(内蒙古农业大学能源与交通工程学院, 呼和浩特 010018)
将沥青混合料耐久性纳入沥青路面设计体系是“交通强国”国家战略建设的重要保障,提出完备、有效、可行的沥青混合料疲劳试验方法与分析手段是其关键的基础研究工作[1-2]。沥青混合料疲劳性能影响因素诸多,主要包括材料、加载频率、试验温度、试验方法等[3]。众多学者从材料角度出发,针对不同的矿质混合料级配类型、沥青种类、体积控制指标及不同外掺剂下的沥青混合料疲劳性能展开研究,得出了众多材料相关因素对沥青混合料疲劳性能的影响规律与影响机理[4-6];文献[7-9]从加载频率角度出发,针对不同波形下频率变化水平对沥青混合料疲劳寿命的影响展开研究,得出疲劳寿命与加载频率之间的指数关系,并将沥青混合料疲劳方程做了进一步改进,得出沥青路面易产生疲劳裂缝所对应的最不利行车条件。研究发现试验温度对疲劳寿命的影响较显著,且其影响水平与试验加载方式有关[10-11]。还有学者从应力水平、加载间歇时间、试件受力模式等细节方面讨论了沥青混合料疲劳寿命随其变化的规律[12-14]。
再生沥青混合料(reclaimed asphalt pavement,RAP)中随着铣刨料掺量的增加,混合料中旧沥青比例增大,使得沥青混合料的硬度增加,更易产生疲劳破坏[15]。基于统计学原理,分别采用极差分析、灰关联分析与方差分析等手段,系统分析了再生沥青混合料中RAP掺量、加载频率、试验温度与应变水平对混合料疲劳性能的影响,并改进了佩尔疲劳模型。
1 试验设计
前期研究已确定再生剂种类、再生剂掺量(7%)和级配类型(AC-16)[3]。试件成型采用澳大利亚IPC global生产的剪切压实仪,切割方式为无齿锯切割,试件尺寸为长×宽×高=(380±5)mm×(63.5±5)mm×(50±5)mm。疲劳试验选用四点弯曲疲劳试验,加载工具为IPC生产的UTM-100万能试验机。
RAP掺量:0、25%、50%;试验温度:10、15、20 ℃;控制应变:600、700、800 με;加载频率:5、7、10 Hz。
2 试验因素对疲劳寿命的影响分析
2.1 疲劳寿命随影响因素变化规律
图1为两个温度水平下不同RAP掺量的再生沥青混合料疲劳寿命Nf随控制应变与加载频率变化折线图。由图1可知,在同一温度下,沥青混合料疲劳寿命随加载频率的增大而减小,随控制应变的增大而减小;在同一控制应变与加载频率水平下,沥青混合料疲劳寿命随RAP掺量的增大而减小。对比图1(a)和图1(b)可知,随着试验温度的升高,在同一RAP掺量、控制应变、加载频率水平下,沥青混合料疲劳寿命随试验温度的升高而升高。即再生沥青混合料的疲劳寿命随RAP掺量、控制应变、加载频率、试验温度4个因素的变化呈现规律性变化,进一步对疲劳寿命与四因素其进行相关性分析。

图1 Nf随试验条件变化规律Fig.1 Variation of Nf with test conditions
2.2 影响因素显著性分析
为讨论4种因素对再生沥青混合料疲劳寿命影响的显著性,对试验数据进行主因素与交互作用显著性分析。表1为主因素间效应检验结果,假定等方差选取最小显著差(least significant difference,LSD),置信区间为95%,则显著性小于0.05即为显著。

表1 主因素间效应检验Table 1 Effect between main factors
由表1可知,主因素RAP掺量、试验温度、控制应变、加载频率对疲劳寿命的影响均表现出显著性,因此四个因素对沥青混合料疲劳寿命的影响是有规律的。RAP掺量×试验温度、RAP掺量×控制应变、RAP掺量×加载频率的交互效应显著性均大于0.05,即为不显著,说明试验温度、控制应变、加载频率对沥青混合料疲劳寿命的影响规律与RAP掺量的变化关系不明显。综上,可认为RAP掺量、试验温度、控制应变、加载频率对沥青混合料疲劳寿命的作用是单独的,在后续疲劳模型的研究中可将四因素作为模型参数进行回归计算,不考虑RAP掺量与试验参数的交互效应。
2.3 影响因素的灰色关联度分析
灰色系统理论提出了灰色关联度的概念,它是指系统中两个因素关联性大小的量度。关联度的大小直接反映系统中的各因素对目标值的影响程度。
设RAP掺量、试验温度、控制应变、加载频率分别为比较数列X1、X2、X3、X4,疲劳寿命为参考数列Y。分辨系数ρ取0.5,将疲劳寿命数据代入式(1)计算出各因素的关联系数εi,将关联系数代入式(2)求出各因素关联度Ri,如表2所示。

表2 各因素与疲劳寿命关联度Table 2 Relevancy between influence factor and Nf
εi(k)=
(1)
(2)
式中:x0为参考数列;xi为比较数列;k为影响因素;n为试验组数。
由表2可知,四因素与沥青混合料疲劳寿命的关联度值大小为控制应变>试验温度>RAP掺量>加载频率,且控制应变的关联度较大,其余三因素关联度数值较为接近。说明试验控制应变对再生沥青混合料疲劳寿命的影响最显著,RAP掺量、试验温度、加载频率的影响程度次之,且此三因素对疲劳寿命的影响程度较接近,即再生沥青路面在服役过程中其耐久性的影响受车辆轴重的影响最大,RAP掺量、环境温度、行车速度对其影响次之。
为进一步验证RAP掺量、环境温度、行车速度对疲劳寿命的影响程度,对此三因素做极差分析。
2.4 影响因素的极差分析
RAP掺量、试验温度、加载频率三因素对疲劳寿命Nf影响的极差分析结果如表3所示,为方便比较数值大小,将3个应变水平下的极差值做归一化处理,即N-极差。
由表3可知,在3个应变水平下,极差值大小顺序均为试验温度>RAP掺量>加载频率。因此,此三因素对疲劳寿命的影响程度即试验温度>RAP掺量>加载频率,与灰色关联度分析结果一致,且极差值较关联度值的区别更加明显。
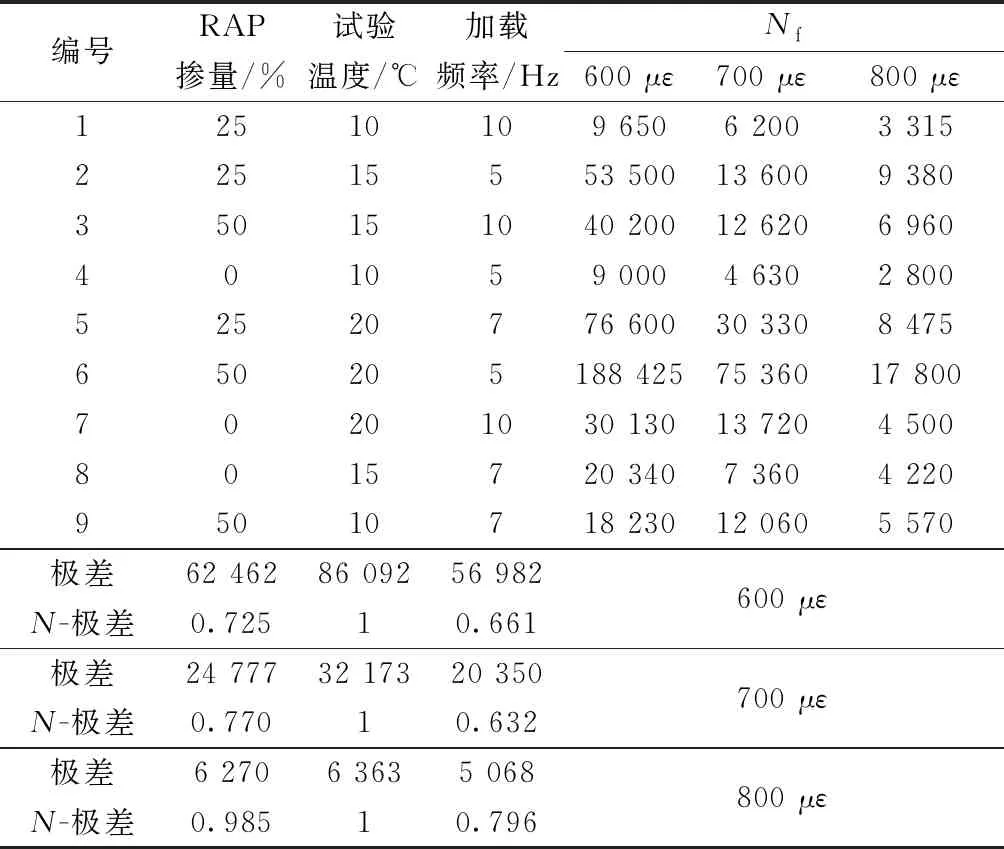
表3 Nf极差分析结果Table 3 Range analysis results of Nf
因此,在分析不同因素对沥青混合料疲劳寿命影响时可采用灰色关联度分析、极差分析与主因素分析相结合的方式,首先确定疲劳寿命与影响因素之间关联的显著性,进一步确定影响因素的影响程度。
3 试验因素对疲劳方程回归参数的影响分析
为进一步研究试验温度、RAP掺量、加载频率与控制应变对沥青混合料疲劳寿命的影响,选取佩尔提出的基于应变的沥青混合料疲劳寿命方程进行分析。
(3)
为简便计算,将等式两边取对数并做简单处理后,变为线性关系可表示为
lgNf=m+klgε
(4)
式中:Nf为疲劳寿命;ε为控制应变;a、b、m、k为模型回归参数,其中,双对数坐标下的疲劳方程中,|k|可反映疲劳寿命与应变水平的敏感性,|k|越大,疲劳曲线越陡,疲劳寿命对应变越敏感;m可反映疲劳曲线线位的高低,m值越大,疲劳寿命越大。
按式(4)对试验数据进行回归分析,回归参数及置信率结果如表4所示。
由表4可知,拟合相关系数均达到85%以上,说明基于应变的沥青混合料疲劳寿命方程适用于再生沥青混合料疲劳寿命的研究。
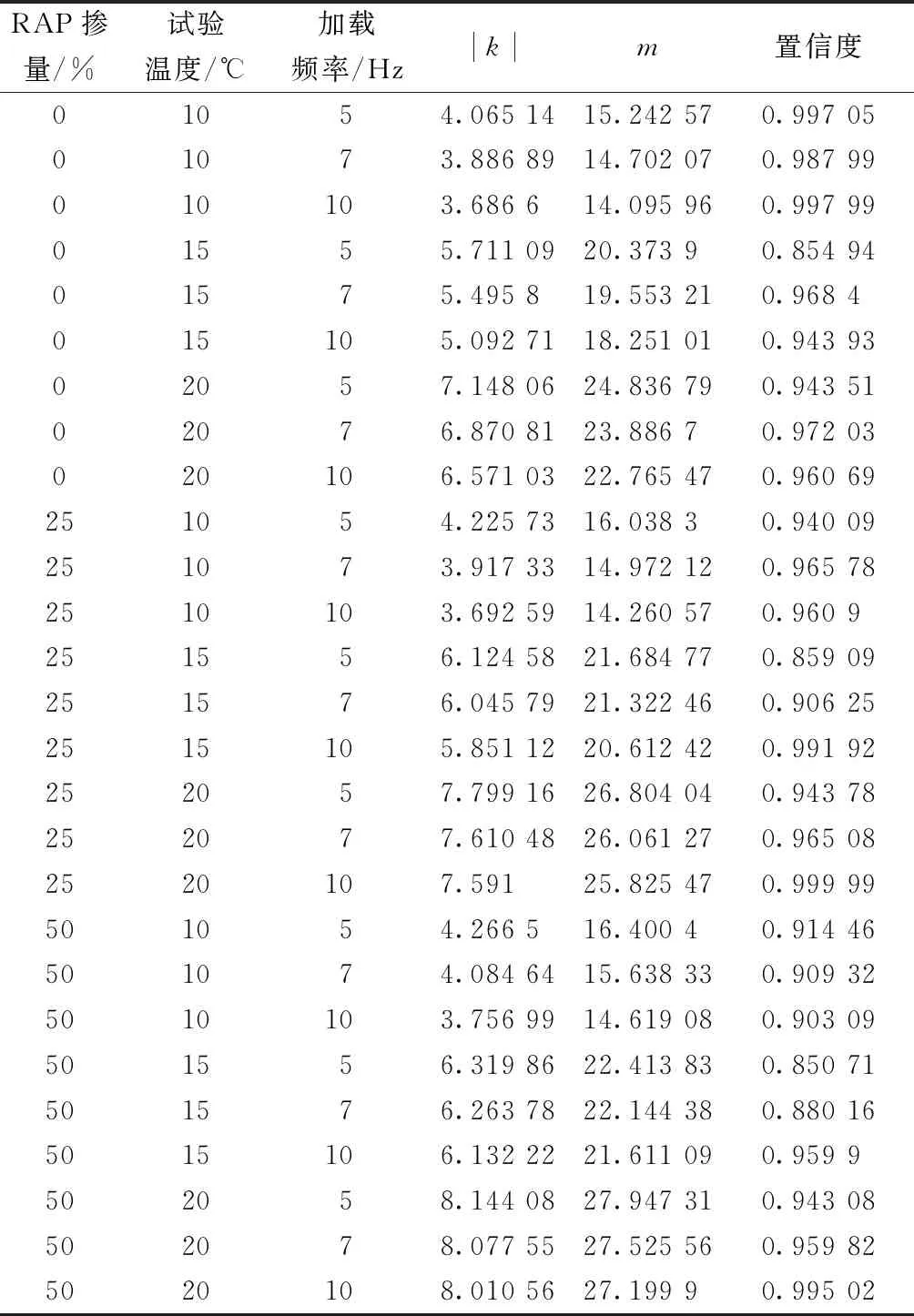
表4 疲劳方程回归参数及置信率Table 4 Regression parameters and confidence rates of fatigue equations
将RAP掺量、试验温度、加载频率与疲劳方程中回归参数的关系做折线图(图2)。
图2为回归参数|k|与m随试验条件变化的情况。由图2可知,m均随RAP掺量的增加而增大,表明随着RAP掺量的增加疲劳寿命在一定范围内提高;同时,|k|也随RAP掺量的增加而增大,即疲劳寿命对应变的敏感性也提高,即在RAP掺量较高时,再生沥青路面的疲劳寿命会随着轴重的增加衰减速度变快,因此,在RAP掺量较高时,再生沥青混合料路面设计中应强调对车辆轴重的控制。
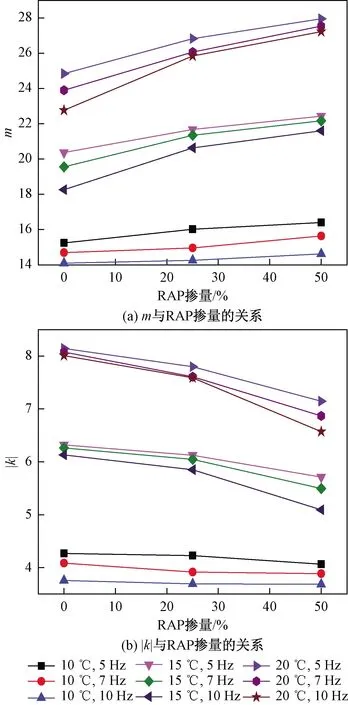
图2 m与|k|随试验条件变化情况Fig.2 Changes of m and |k| with the test conditions
m随加载频率的增大而减小,表明随着加载频率的增大,再生沥青路面疲劳寿命减小,这主要是由于加载频率的增大使试验的加载间歇变短,沥青混合料的自愈合程度减弱造成的;|k|随加载频率的增大而减小,表明高频加载方式下,疲劳寿命对控制应变的敏感性减弱,这主要是由于加载频率的增大使得加载时间变短,沥青混合料在单次荷载作用下损伤减小所造成。
|k|与m均随温度的升高而增大,表明随着温度的升高,再生沥青混合料疲劳寿命增大,疲劳寿命对应变的敏感性减弱。这主要是由于沥青是典型的温度敏感性材料,随着温度的升高,黏性增强,弹性减弱,从而引起应变滞后,导致劲度模量的衰减速率降低且随应变变化的敏感性降低所致。
4 试验因素对疲劳方程的影响分析
4.1 疲劳方程参数影响显著性分析
由图2分析可知,|k|和m随RAP掺量、试验温度、加载频率的变化呈现规律性,若影响显著,则可将三因素引入佩尔疲劳寿命模型。表5为|k|和m与三因素的主因素显著性检验结果,假定等方差选取LSD与S-N-K(一种有效划分相似性子集的方法),置信区间为95%。
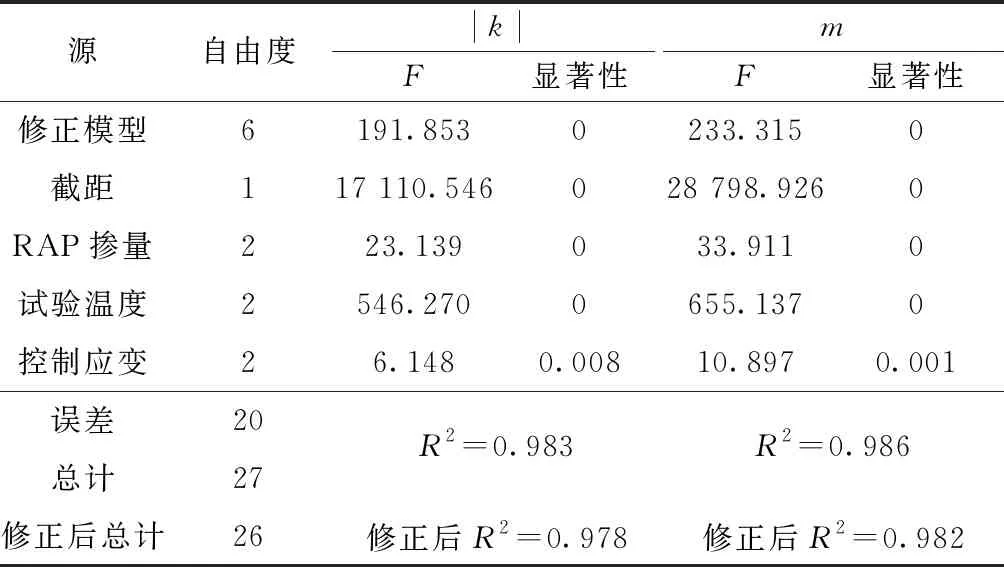
表5 因素对|k|和m的影响结果Table 5 The effect of factors on |k| and m
由表5可知,主因素RAP掺量、试验温度、加载频率对|k|和m的影响显著性均小于0.05,说明佩尔模型中的两个系数与以上三因素的关联度较高,因此可假设疲劳寿命方程为
lgNf=f1(R,T,f)+f2(R,T,f)lgε
(5)
式(5)中:f1(R,T,f)、f2(R,T,f)为RAP掺量、试验温度、加载频率的函数;R为RAP掺量;T为诚验温度;f为加载频率。
4.2 函数验证
为验证式(5)可靠性,对不同因素水平下的|k|和m做非线性拟合,选取f1(R,T,f)、f2(R,T,f)的函数形式为
(6)
式(6)中:y为因变量|k|和m;x1、x2、x3为自变量RAP掺量、试验温度、加载频率;A、B、c、d、e为拟合参数。
由于上述分析自变量RAP掺量,试验温度,加载频率三因素之间交互作用不明显,式(6)中不考虑自变量的相互影响,拟合结果如表6所示。
由表6可知,通过式6对因变量|k|、m与自变量RAP掺量、试验温度、加载频率进行非线性拟合,可靠度均大于0.9,说明佩尔疲劳模型的参数|k|和m可以用含有RAP掺量、试验温度、加载频率3个参数的函数来表达,证明了式5作为改进的疲劳模型的正确性。

表6 参数拟合结果Table 6 Results of parameter fitting
综上,改进的疲劳模型除含有控制应变参数以外,还包含了再生沥青路面的RAP掺量、试验温度、加载频率3个参数,即此模型可以描述再生沥青路面疲劳寿命在RAP掺量、温度、行车速度、车辆轴重四种因素耦合作用下的情况,较佩尔疲劳模型表达更全面。
5 结论
(1)再生沥青混合料的疲劳寿命与RAP掺量、控制应变、加载频率、试验温度具有相关性,疲劳寿命随RAP掺量的增大而减小,随控制应变的增大而减小,随加载频率的增大而减小,随试验温度的升高而增大。
(2)RAP掺量、控制应变、加载频率、试验温度对疲劳寿命影响的显著性均大于95%,但RAP掺量与其他三因素的交互效应显著性不明显;四因素对再生沥青混合料疲劳寿命影响程度为控制应变>试验温度>RAP掺量>加载频率。
(3)佩尔疲劳模型适用于再生沥青混合料疲劳寿命研究,此模型中的系数与RAP掺量、加载频率、试验温度相关性较高,通过非线性拟合可将以上3个因素引入模型,改进后的疲劳模型方程为lgNf=f1(R,T,f)+f2(R,T,f)lgε。
